- Головна
- Готові шкільні презентації
- Презентація на тему «Ймовірності випадкових подій. Аналіз випадкових величин»
Презентація на тему «Ймовірності випадкових подій. Аналіз випадкових величин»
332
Слайд #1
Виконали учні 11-А класу
Михайлюк Святослав
Нізієнко Костянтин
Ймовірності випадкових подій. Аналіз випадкових величин
Михайлюк Святослав
Нізієнко Костянтин
Ймовірності випадкових подій. Аналіз випадкових величин

Слайд #2
2
ЗМІСТ
Випадкова подія.
Статистичне та класичне означення ймовірності випадкової події.
Теоретико-множинний розгляд випадкових подій.
Умовна ймовірність.
Теореми множення ймовірностей.
Теореми додавання ймовірностей.
Аналіз випадкових величин
ЗМІСТ
Випадкова подія.
Статистичне та класичне означення ймовірності випадкової події.
Теоретико-множинний розгляд випадкових подій.
Умовна ймовірність.
Теореми множення ймовірностей.
Теореми додавання ймовірностей.
Аналіз випадкових величин

Слайд #3
3
Основні поняття теорії ймовірностей
Теорія ймовірностей вивчає масові випадкові події, які характеризуються стійкою частотою їх появи.
Випадковою подією в теорії ймовірності називають всякий факт, який в результаті досліду (спостереження) може відбутися або не відбутися.
Різні випадкові події позначаються латинськими буквами А, В, С… .
Основні поняття теорії ймовірностей
Теорія ймовірностей вивчає масові випадкові події, які характеризуються стійкою частотою їх появи.
Випадковою подією в теорії ймовірності називають всякий факт, який в результаті досліду (спостереження) може відбутися або не відбутися.
Різні випадкові події позначаються латинськими буквами А, В, С… .

Слайд #4
4
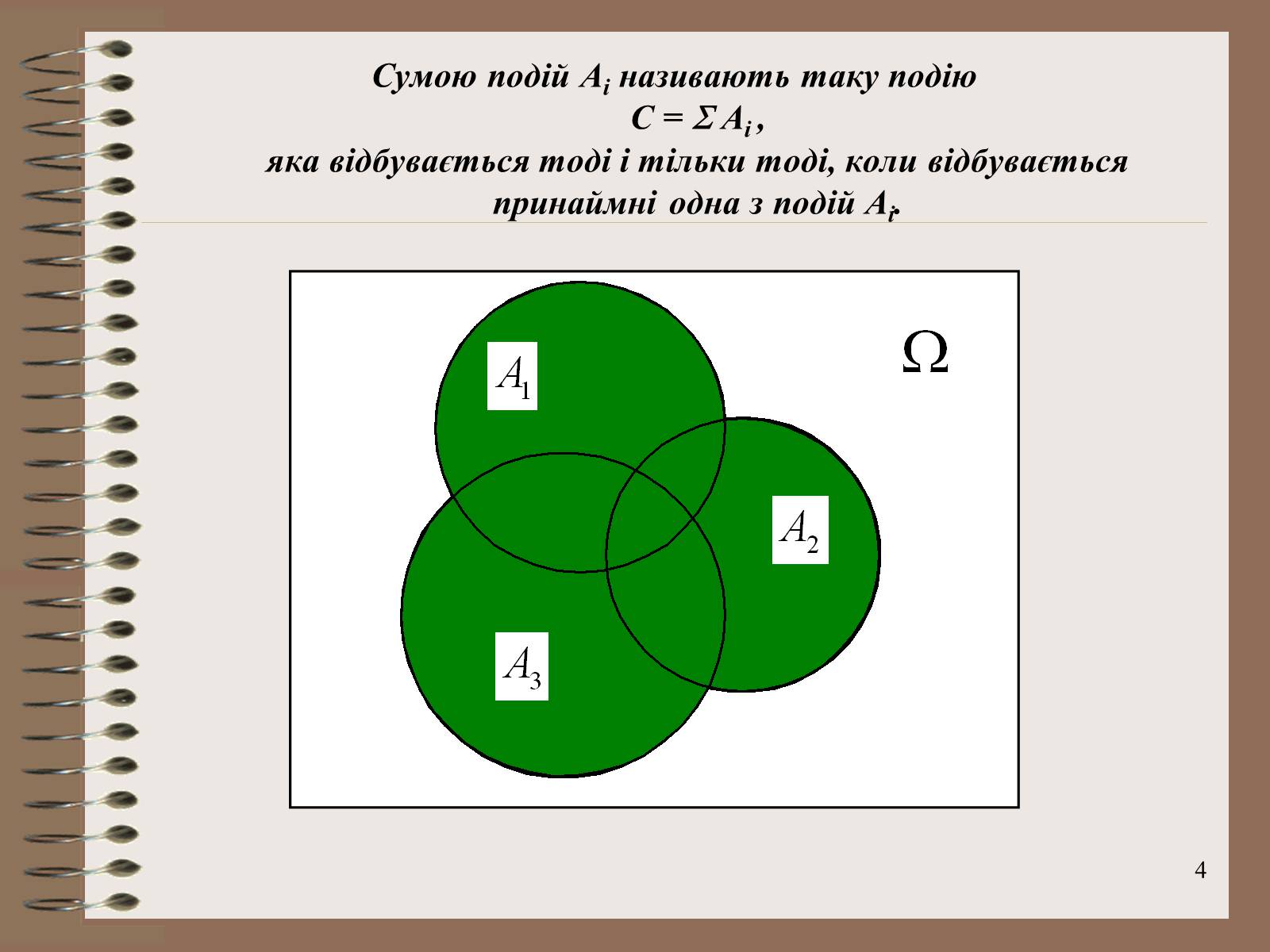
Сумою подій Аі називають таку подію C = Ai , яка відбувається тоді і тільки тоді, коли відбувається принаймні одна з подій Аі.
Сумою подій Аі називають таку подію C = Ai , яка відбувається тоді і тільки тоді, коли відбувається принаймні одна з подій Аі.
Слайд #5
5
Приклад.
Подія A – “випадання цифри 1 при одноразовому підкиданні грального кубика”. Подія B – “випадання цифри 2 при одноразовому підкиданні грального кубика”.
Сумою A+B зазначених подій є подія C – “випадання цифри, не більшої двох, при одноразовому підкиданні грального кубика”.
Приклад.
Подія A – “випадання цифри 1 при одноразовому підкиданні грального кубика”. Подія B – “випадання цифри 2 при одноразовому підкиданні грального кубика”.
Сумою A+B зазначених подій є подія C – “випадання цифри, не більшої двох, при одноразовому підкиданні грального кубика”.

Слайд #6
6
Операції над подіями
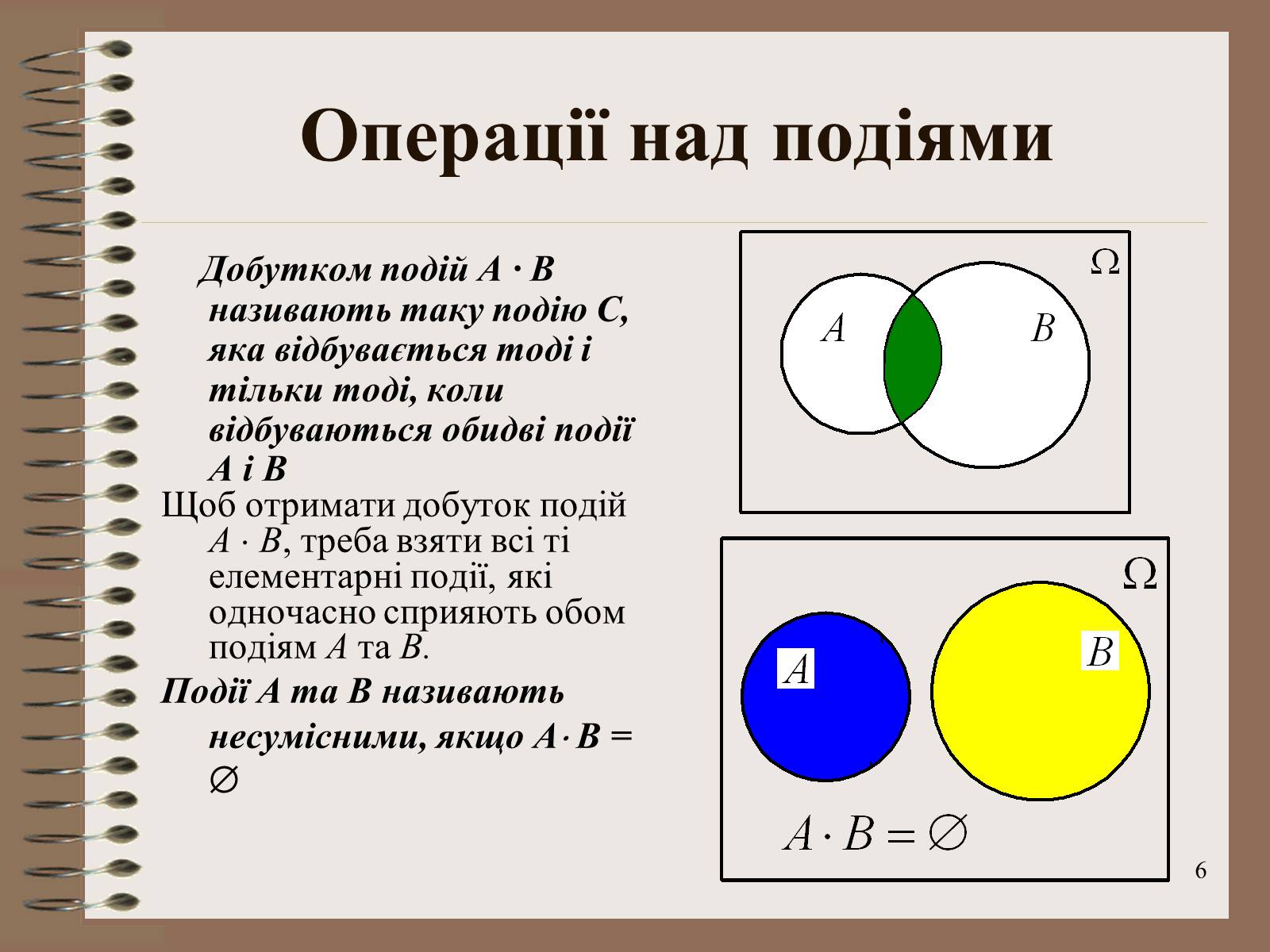
Добутком подій А · В називають таку подію С, яка відбувається тоді і тільки тоді, коли відбуваються обидві події А і В
Щоб отримати добуток подій А В, треба взяти всі ті елементарні події, які одночасно сприяють обом подіям А та В.
Події А та В називають несумісними, якщо А В =
Операції над подіями
Добутком подій А · В називають таку подію С, яка відбувається тоді і тільки тоді, коли відбуваються обидві події А і В
Щоб отримати добуток подій А В, треба взяти всі ті елементарні події, які одночасно сприяють обом подіям А та В.
Події А та В називають несумісними, якщо А В =
Слайд #7
7
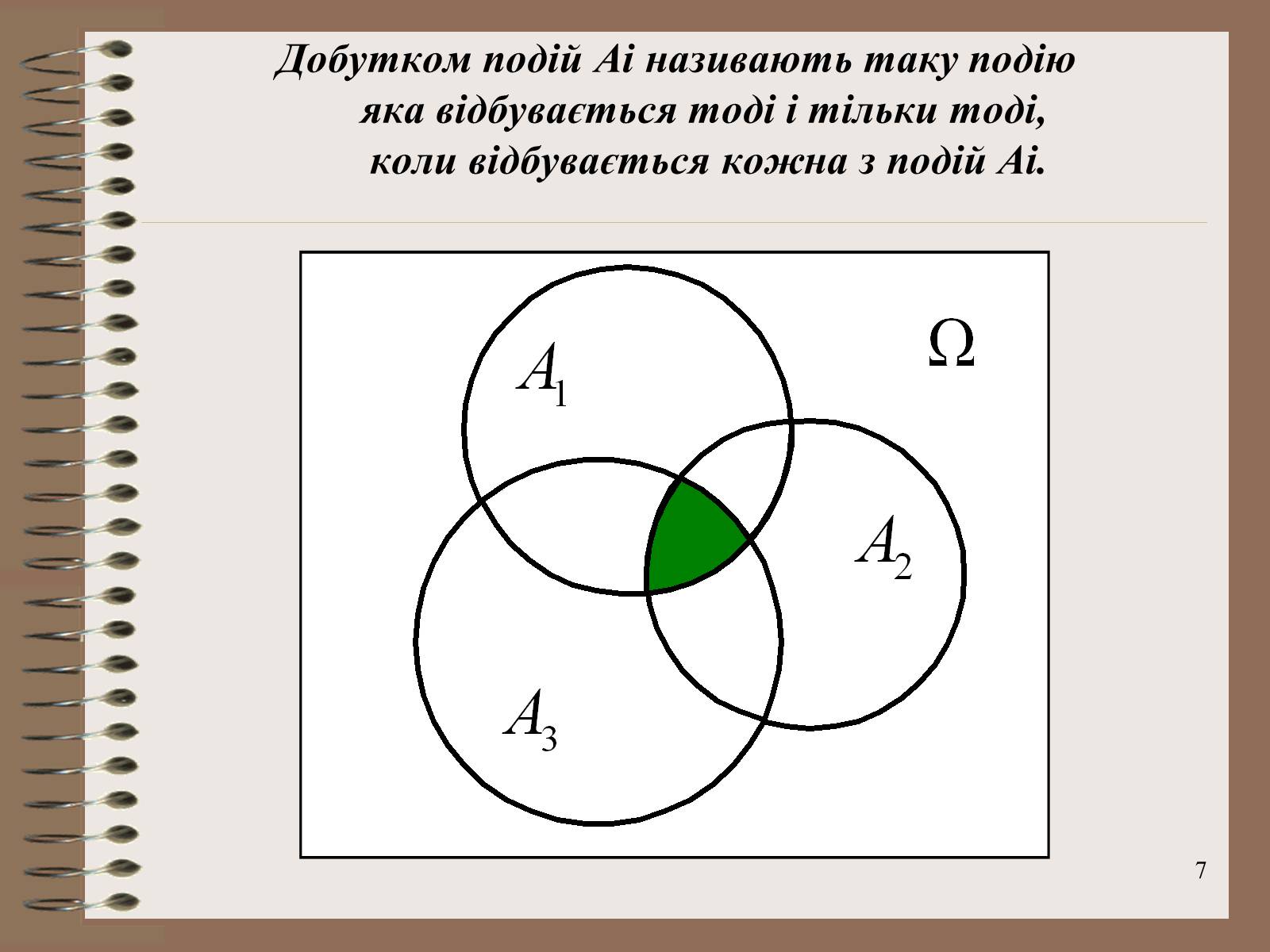
Добутком подій Аі називають таку подію яка відбувається тоді і тільки тоді, коли відбувається кожна з подій Аі.
Добутком подій Аі називають таку подію яка відбувається тоді і тільки тоді, коли відбувається кожна з подій Аі.
Слайд #8
8
Приклад.
Подія A – “студент отримав екзаменаційний білет з парним номером”.
Подія B – “студент отримав екзаменаційний білет з номером, кратним трьом”. Добутком A×B зазначених подій є подія C – “студент отримав екзаменаційний білет з номером, кратним шести”.
Приклад.
Подія A – “студент отримав екзаменаційний білет з парним номером”.
Подія B – “студент отримав екзаменаційний білет з номером, кратним трьом”. Добутком A×B зазначених подій є подія C – “студент отримав екзаменаційний білет з номером, кратним шести”.

Слайд #9
9
Операції над подіями
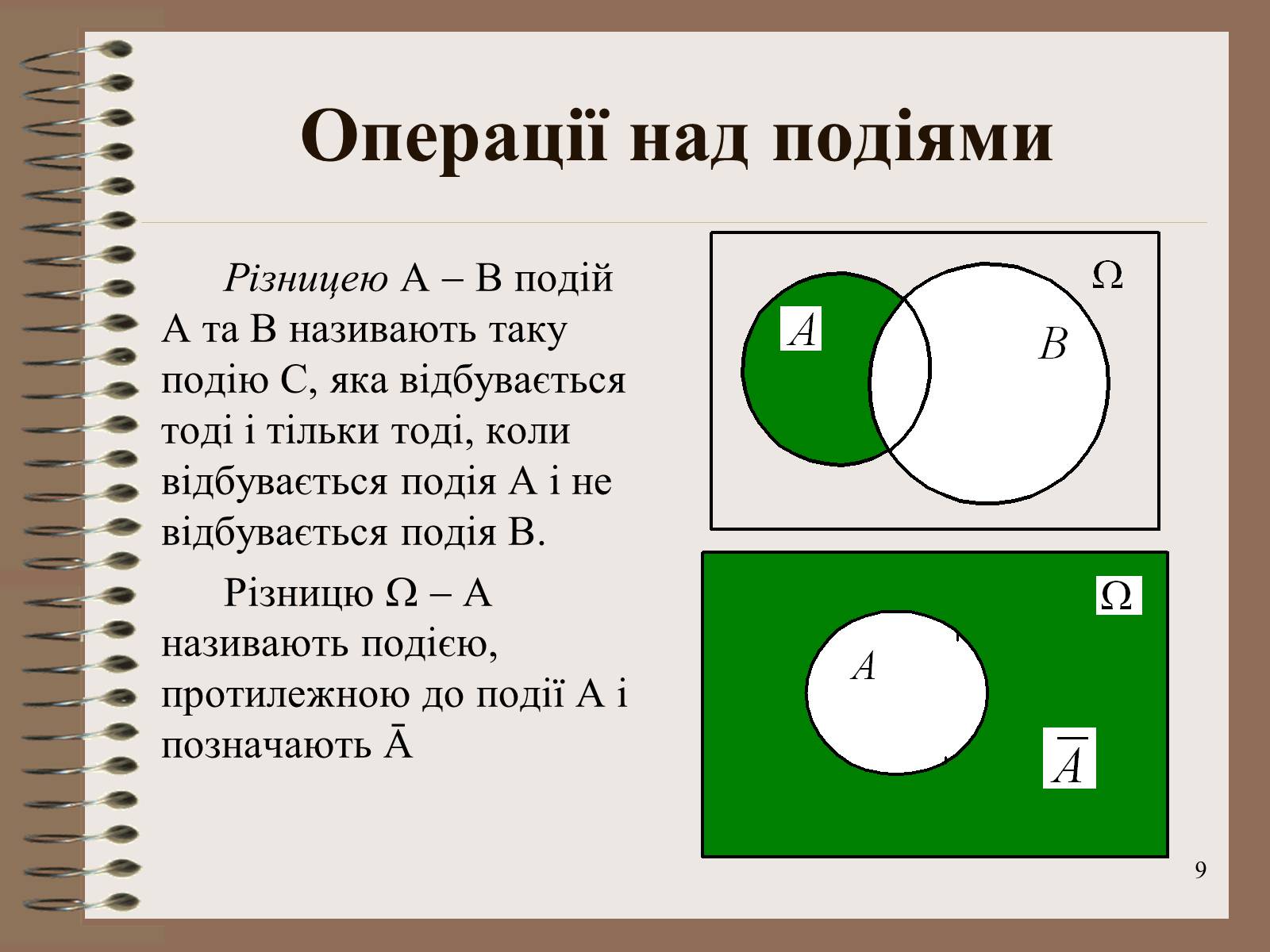
Різницею А В подій А та В називають таку подію С, яка відбувається тоді і тільки тоді, коли відбувається подія А і не відбувається подія В.
Різницю А називають подією, протилежною до події А і позначають Ā
Операції над подіями
Різницею А В подій А та В називають таку подію С, яка відбувається тоді і тільки тоді, коли відбувається подія А і не відбувається подія В.
Різницю А називають подією, протилежною до події А і позначають Ā
Слайд #10
10
Означення випадкової події
Випадковими подіями або просто подіями називають такі підмножини простору Ω, які утворюють деяку сукупність S, що задовольняє три основні умови:
1s. S
- вірогідна подія завжди належить цій сукупності;
2s. Якщо А S, то Ā S
- кожна подія належить цій сукупності разом зі своєю протилежною подією;
3s. Якщо Аi S, i N, то Аi S
- для будь-яких подій, що належать даній сукупності, їх сума також належить цій сукупності.
Таку сукупність S називають простором подій. Кожну підмножину , що входить до S, вважають подією, а всі інші підмножини Ω не вважають подіями.
Означення випадкової події
Випадковими подіями або просто подіями називають такі підмножини простору Ω, які утворюють деяку сукупність S, що задовольняє три основні умови:
1s. S
- вірогідна подія завжди належить цій сукупності;
2s. Якщо А S, то Ā S
- кожна подія належить цій сукупності разом зі своєю протилежною подією;
3s. Якщо Аi S, i N, то Аi S
- для будь-яких подій, що належать даній сукупності, їх сума також належить цій сукупності.
Таку сукупність S називають простором подій. Кожну підмножину , що входить до S, вважають подією, а всі інші підмножини Ω не вважають подіями.

Слайд #11
11
Простір випадкових подій
Простір подій S можна утворювати багатьма способами. Головним при побудові простору подій є виконання основних властивостей подій 1s – 3s, які можна назвати правилами побудови простору подій або правилами визначення випадкових подій.
Наприклад, при підкиданні грального кубика простір елементарних подій 1, 2, 3, 4, 5, 6. Нам важливо, щоб подією було випадання парної кількості очок. Тоді в S повинні входити Ω, , А = {2, 4, 6} (за умовою завдання) і Ā= {1, 3, 5} (за властивістю 2s).
Cукупність , , 1, 3, 5, 2, 4, 6 можна вважати простором випадкових подій S і при цьому кожен елемент цієї сукупності є випадковою подією. Усі інші підмножини при цьому не вважаються подіями.
Простір випадкових подій
Простір подій S можна утворювати багатьма способами. Головним при побудові простору подій є виконання основних властивостей подій 1s – 3s, які можна назвати правилами побудови простору подій або правилами визначення випадкових подій.
Наприклад, при підкиданні грального кубика простір елементарних подій 1, 2, 3, 4, 5, 6. Нам важливо, щоб подією було випадання парної кількості очок. Тоді в S повинні входити Ω, , А = {2, 4, 6} (за умовою завдання) і Ā= {1, 3, 5} (за властивістю 2s).
Cукупність , , 1, 3, 5, 2, 4, 6 можна вважати простором випадкових подій S і при цьому кожен елемент цієї сукупності є випадковою подією. Усі інші підмножини при цьому не вважаються подіями.

Слайд #12
12
Статистична ймовірність події
Нехай дано експеримент і визначено простір елементарних подій та простір подій S. Для цього експерименту проведено n випробувань і при цьому фіксована елементарна подія е відбулася m раз, 0 ≤ т ≤ n.
Число m випробувань, у яких відбулася елементарна подія е називається її абсолютною частотою, а відношення m до n називається відносною частотою елементарної події е в даній серії з n випробувань.
Відносна частота елементарної події е характеризує середню можливість її відбування у кожному з n випробувань.
Позначається і обчислюється за формулою
Статистична ймовірність події
Нехай дано експеримент і визначено простір елементарних подій та простір подій S. Для цього експерименту проведено n випробувань і при цьому фіксована елементарна подія е відбулася m раз, 0 ≤ т ≤ n.
Число m випробувань, у яких відбулася елементарна подія е називається її абсолютною частотою, а відношення m до n називається відносною частотою елементарної події е в даній серії з n випробувань.
Відносна частота елементарної події е характеризує середню можливість її відбування у кожному з n випробувань.
Позначається і обчислюється за формулою

Слайд #13
13
Статистична ймовірність і кількість випробувань
Статистична ймовірність події може залежати від кількості n випробувань і, зрозуміло, що коли змінюється кількість випробувань, то може змінюватися і статистична ймовірність. Виникає питання – на скільки суттєві такі зміни?
Розглянемо приклад.
1. В таблиці подано результати експерименту з підкиданням монети. Було проведено 10 серій з 1000 підкидань:
Статистична ймовірність і кількість випробувань
Статистична ймовірність події може залежати від кількості n випробувань і, зрозуміло, що коли змінюється кількість випробувань, то може змінюватися і статистична ймовірність. Виникає питання – на скільки суттєві такі зміни?
Розглянемо приклад.
1. В таблиці подано результати експерименту з підкиданням монети. Було проведено 10 серій з 1000 підкидань:

Слайд #14
14
Визначення ймовірності події
За умови рівноможливості елементарних подій, що утворюють простір , ймовірність будь-якої події А обчислюється за формулою
де k – кількість елементарних подій, що сприяють події А, т – кількість усіх елементарних подій простору .
Обчислення ймовірностей за вказаним правилом називають обчисленням ймовірності події за класичною схемою.
Визначення ймовірності події
За умови рівноможливості елементарних подій, що утворюють простір , ймовірність будь-якої події А обчислюється за формулою
де k – кількість елементарних подій, що сприяють події А, т – кількість усіх елементарних подій простору .
Обчислення ймовірностей за вказаним правилом називають обчисленням ймовірності події за класичною схемою.

Слайд #15
15
Властивості ймовірності події
Властивості ймовірності події

Слайд #16
16
Алгоритмічний припис обчислення ймовірності події за класичною схемою
Опиши експеримент, про який йдеться в умові задачі та відповідний простір елементарних подій .
Обґрунтуй рівноможливість елементарних подій і визнач, з яких елементарних подій складається подія А.
Визнач кількість т елементарних подій простору Ω.
Визнач кількість k елементарних подій, що сприяють події А.
Обчисли ймовірність події А за формулою
Алгоритмічний припис обчислення ймовірності події за класичною схемою
Опиши експеримент, про який йдеться в умові задачі та відповідний простір елементарних подій .
Обґрунтуй рівноможливість елементарних подій і визнач, з яких елементарних подій складається подія А.
Визнач кількість т елементарних подій простору Ω.
Визнач кількість k елементарних подій, що сприяють події А.
Обчисли ймовірність події А за формулою

Слайд #17
17
Комбінаторика
При розв'язуванні задач з теорії ймовірностей не завжди можливо побудувати повну групу елементарних подій через великий обсяг роботи. Тому обмежуються тільки обчисленням кількості всіх елементарних подій, а також кількості тих із них, що сприяють
певній випадковій події. При цьому використовують правило множення, перестановки, розміщення та комбінації.
Комбінаторика
При розв'язуванні задач з теорії ймовірностей не завжди можливо побудувати повну групу елементарних подій через великий обсяг роботи. Тому обмежуються тільки обчисленням кількості всіх елементарних подій, а також кількості тих із них, що сприяють
певній випадковій події. При цьому використовують правило множення, перестановки, розміщення та комбінації.
