- Головна
- Готові шкільні презентації
- Презентація на тему «Алфавіт Pascal»
Презентація на тему «Алфавіт Pascal»
299
Слайд #1
Алфавіт мови програмування Pascal.Величини. Типи даних.Набір функцій та операцій для кожного з типів.

Слайд #2
Алфавіт мови програмування Паскаль складається з:
1. Символів, що використовуються для імен змінних:
2. Символів-розділювачів:
Малі та великі літери латинського алфавіту;
Арабські цифри від 0 до 9;
Символ підкреслення _ .
Символ пробілу;
Розділові знаки: . , ‘ : ;
3. Спеціальних символів: + - * / { } [ ] ( ) < > = # $ @
4. Складених символів: >= <= <> := ..
5. Зарезервованих слів: if, else, read, begin тощо.
1. Символів, що використовуються для імен змінних:
2. Символів-розділювачів:
Малі та великі літери латинського алфавіту;
Арабські цифри від 0 до 9;
Символ підкреслення _ .
Символ пробілу;
Розділові знаки: . , ‘ : ;
3. Спеціальних символів: + - * / { } [ ] ( ) < > = # $ @
4. Складених символів: >= <= <> := ..
5. Зарезервованих слів: if, else, read, begin тощо.

Слайд #3
Величини – це дані, що обробляються програмами.
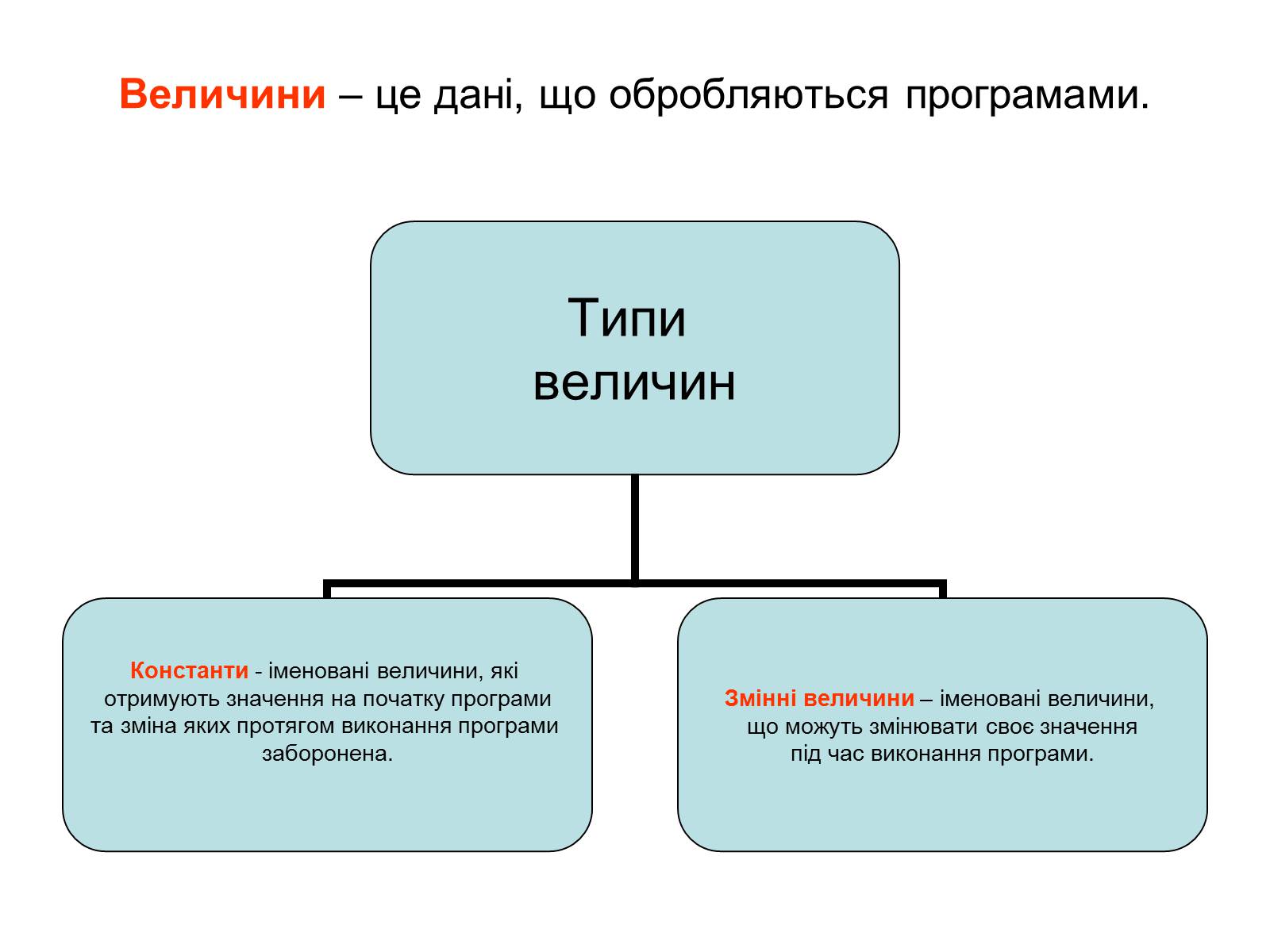
Слайд #4
Формат опису сталих величин
Const <ідентифікатор>=<значення величини>;
Наприклад,
Const max=1000;
pi=3.14;
Const <ідентифікатор>=<значення величини>;
Наприклад,
Const max=1000;
pi=3.14;

Слайд #5
Формат опису змінних величин
Var <ідентифікатор> : <тип величин>;
Наприклад,
Var sum1, sum2: real;
n: integer;
Var <ідентифікатор> : <тип величин>;
Наприклад,
Var sum1, sum2: real;
n: integer;

Слайд #6
Типи даних у мові програмування Паскаль поділяються на:
Скалярні (прості)
Стандартні (цілі, дійсні, літерні, булеві);
Типи користувача.
Структуровані (складені).
Скалярні (прості)
Стандартні (цілі, дійсні, літерні, булеві);
Типи користувача.
Структуровані (складені).

Слайд #7
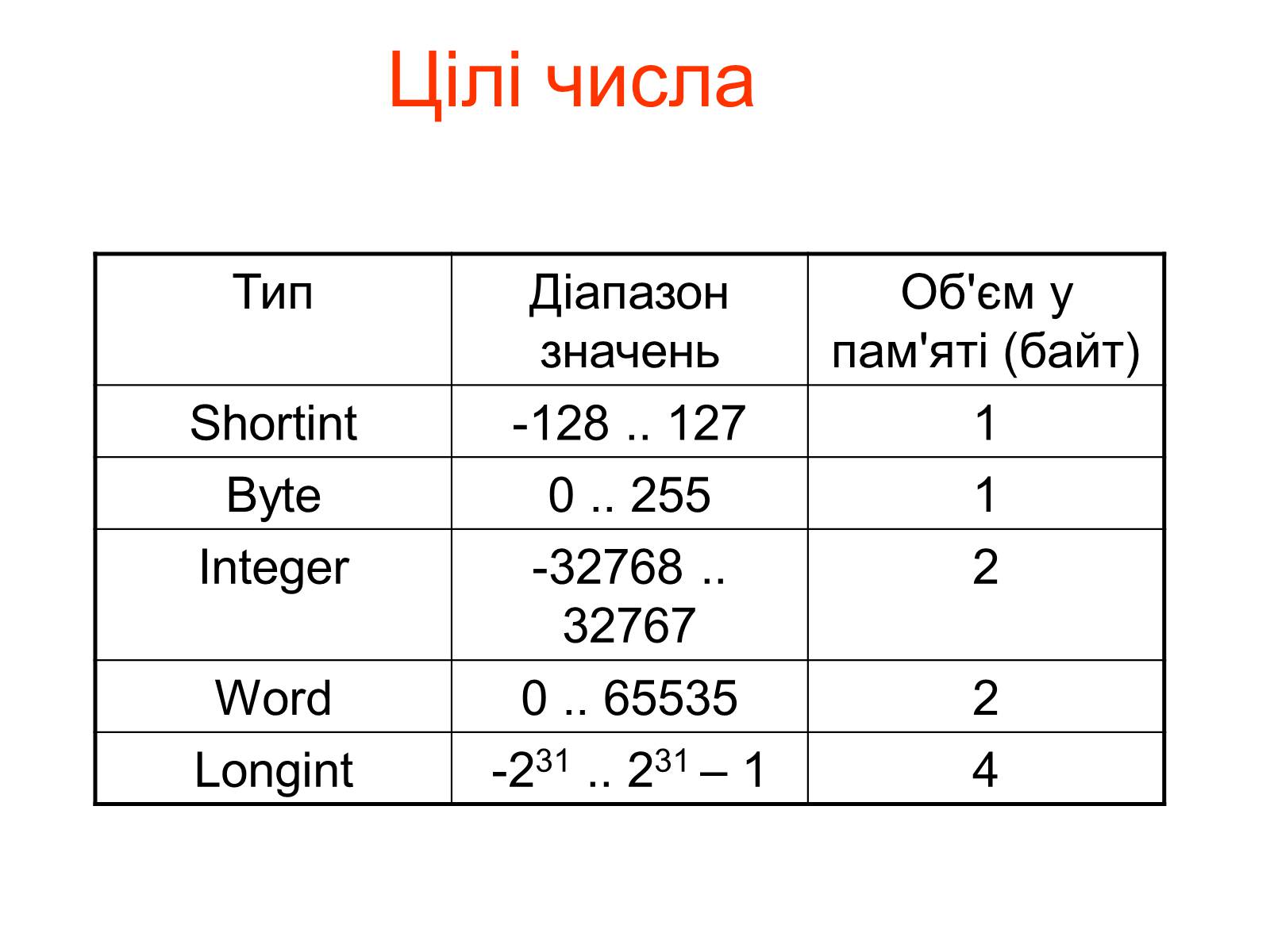
Цілі числа
Тип
Діапазон значень
Об'єм у пам'яті (байт)
Shortint
-128 .. 127
1
Byte
0 .. 255
1
Integer
-32768 .. 32767
2
Word
0 .. 65535
2
Longint
-231 .. 231 – 1
4
Тип
Діапазон значень
Об'єм у пам'яті (байт)
Shortint
-128 .. 127
1
Byte
0 .. 255
1
Integer
-32768 .. 32767
2
Word
0 .. 65535
2
Longint
-231 .. 231 – 1
4
Слайд #8
Операції над цілими числами
ОпераціяtПозначення
Додаванняtt+
Відніманняtt-
Множенняtt*
Діленняtt/
Ціла частина від
діленняttdiv
Остача від діленняttmod
Рівністьtt=
Не рівністьtt<>
Меншеtt<
Менше або рівнеtt<=
Більшеtt>
Більше або рівнеtt>=
ОпераціяtПозначення
Додаванняtt+
Відніманняtt-
Множенняtt*
Діленняtt/
Ціла частина від
діленняttdiv
Остача від діленняttmod
Рівністьtt=
Не рівністьtt<>
Меншеtt<
Менше або рівнеtt<=
Більшеtt>
Більше або рівнеtt>=

Слайд #9
Процедура та функції, що використовуються для цілих чисел
Abs(x)tфункція, що знаходить модуль числа Х
Sqr(x)tфункція, що знаходить квадрат числа Х
Inc(x,y)tфункція, що збільшує tзначення Х на tвеличину У
Dec(x,y)tфункція, що зменшує tзначення Х на tвеличину У
Succ(x)tфункція, що знаходить елемент з tнаступним порядковим номером
Pred(x)tфункція, що знаходить елемент з tпопереднім порядковим номером
Random (x)tгенерує значення випадкового числа від 0 tдо Х.
Odd(x)tфункція, що визначає непарність числа Х.
Abs(x)tфункція, що знаходить модуль числа Х
Sqr(x)tфункція, що знаходить квадрат числа Х
Inc(x,y)tфункція, що збільшує tзначення Х на tвеличину У
Dec(x,y)tфункція, що зменшує tзначення Х на tвеличину У
Succ(x)tфункція, що знаходить елемент з tнаступним порядковим номером
Pred(x)tфункція, що знаходить елемент з tпопереднім порядковим номером
Random (x)tгенерує значення випадкового числа від 0 tдо Х.
Odd(x)tфункція, що визначає непарність числа Х.

Слайд #10
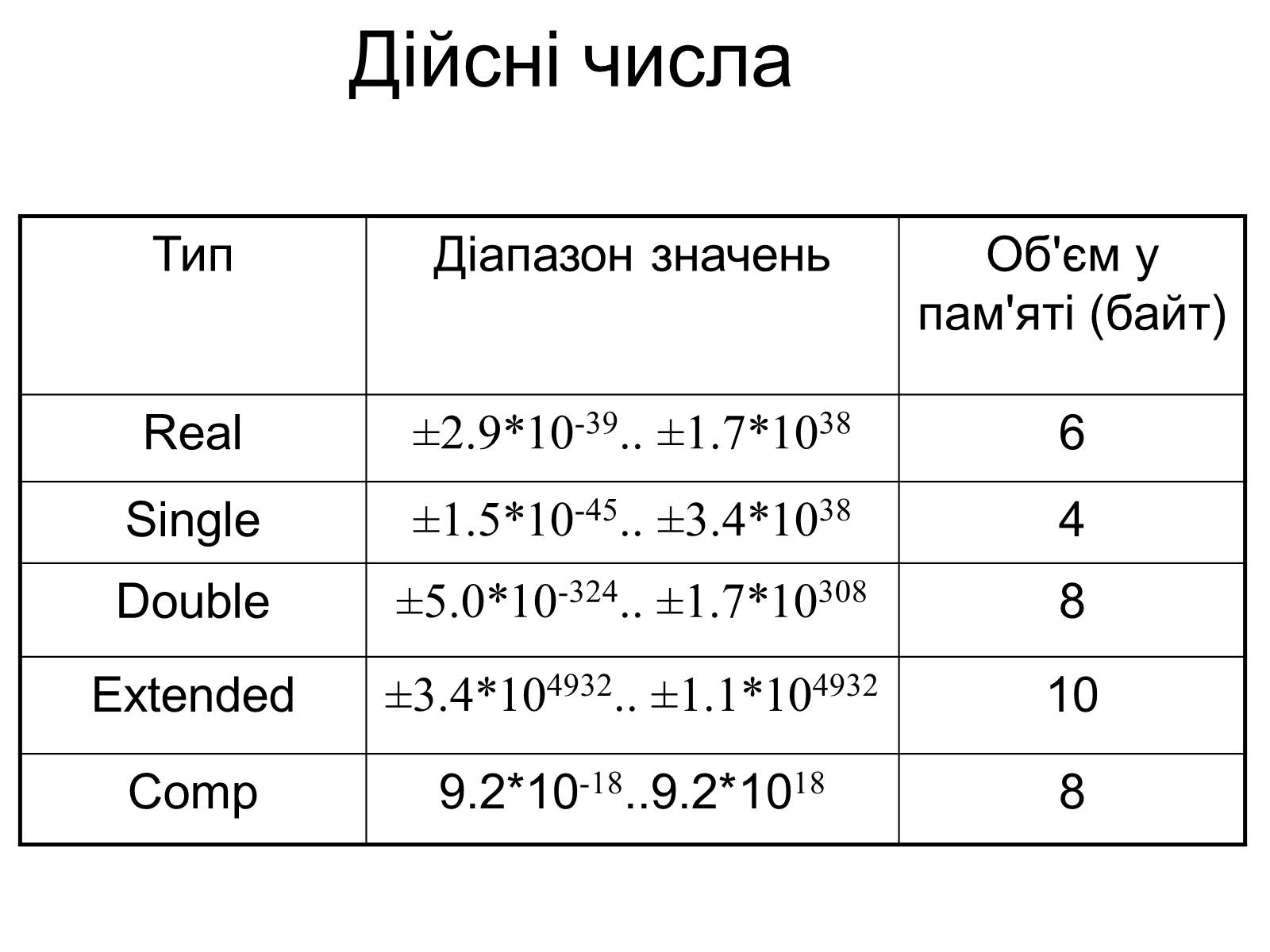
Дійсні числа
Тип
Діапазон значень
Об'єм у пам'яті (байт)
Real
±2.9*10-39.. ±1.7*1038
6
Single
±1.5*10-45.. ±3.4*1038
4
Double
±5.0*10-324.. ±1.7*10308
8
Extended
±3.4*104932.. ±1.1*104932
10
Comp
9.2*10-18..9.2*1018
8
Тип
Діапазон значень
Об'єм у пам'яті (байт)
Real
±2.9*10-39.. ±1.7*1038
6
Single
±1.5*10-45.. ±3.4*1038
4
Double
±5.0*10-324.. ±1.7*10308
8
Extended
±3.4*104932.. ±1.1*104932
10
Comp
9.2*10-18..9.2*1018
8
Слайд #11
Операції над дійсними числами
ОпераціяtПозначення
Додаванняtt+
Відніманняtt-
Множенняtt*
Діленняtt/
Рівністьtt=
Не рівністьtt<>
Меншеtt<
Менше або рівнеtt<=
Більшеtt>
Більше або рівнеtt>=
ОпераціяtПозначення
Додаванняtt+
Відніманняtt-
Множенняtt*
Діленняtt/
Рівністьtt=
Не рівністьtt<>
Меншеtt<
Менше або рівнеtt<=
Більшеtt>
Більше або рівнеtt>=

Слайд #12
Процедури та функції для роботи над дійсними величинами
Abs(x)tфункція, що знаходить модуль числа Х
Sqr(x)tфункція, що знаходить квадрат числа Х
Sqrt(x)tфункція, що знаходить корінь квадратний tвід Х
Ln(x)tфункція, що знаходить логарифм tнатуральний від Х
Exp(x)tзнаходить ех
Sin(x)tзнаходить синус від Х
Cos(x)tзнаходить косинус від Х
Arctan(x)tзнаходить арктангенс від Х
Trunc(x)tзнаходить цілу частину від Х, при цьому tотримуємо tрезультат цілого типу
Round(x)tзаокруглює число до найближчого цілого
Int(x)tзнаходить цілу частину числа Х, при цьому tотримуємо результат дійсного типу
Frac(x)tзнаходить дробову частину числа Х, отримуємо tрезультат дійсного типу
Abs(x)tфункція, що знаходить модуль числа Х
Sqr(x)tфункція, що знаходить квадрат числа Х
Sqrt(x)tфункція, що знаходить корінь квадратний tвід Х
Ln(x)tфункція, що знаходить логарифм tнатуральний від Х
Exp(x)tзнаходить ех
Sin(x)tзнаходить синус від Х
Cos(x)tзнаходить косинус від Х
Arctan(x)tзнаходить арктангенс від Х
Trunc(x)tзнаходить цілу частину від Х, при цьому tотримуємо tрезультат цілого типу
Round(x)tзаокруглює число до найближчого цілого
Int(x)tзнаходить цілу частину числа Х, при цьому tотримуємо результат дійсного типу
Frac(x)tзнаходить дробову частину числа Х, отримуємо tрезультат дійсного типу

Слайд #13
Обчислення ху
X>0tttexp(y*ln(x))
X=0ttt1
X<0, y - парнеtttexp(y*ln(abs(x)))
X<0, y – непарнеt-exp(y*ln(abs(x)))
X>0tttexp(y*ln(x))
X=0ttt1
X<0, y - парнеtttexp(y*ln(abs(x)))
X<0, y – непарнеt-exp(y*ln(abs(x)))

Слайд #14
Подання деяких математичних та тригонометричних функцій, що обчислюються через додаткові вирази:
Logyxtln(X)/ln(Y)
Lg Xtln(X)/ln(10)
Tg Xtsin(X)/cos(X)
Ctg Xtcos(X)/sin(X)
Arcsin Xtarctan(X/sqrt(1-sqr(X)))
Arccos Xtarctan((1-sqr(X))/X)
Arcctg Xt1/arctan(X)
Logyxtln(X)/ln(Y)
Lg Xtln(X)/ln(10)
Tg Xtsin(X)/cos(X)
Ctg Xtcos(X)/sin(X)
Arcsin Xtarctan(X/sqrt(1-sqr(X)))
Arccos Xtarctan((1-sqr(X))/X)
Arcctg Xt1/arctan(X)
