- Головна
- Готові шкільні презентації
- Презентація на тему «MS Exsel»
Презентація на тему «MS Exsel»
301
Слайд #1
MS Exsel
Розв'язування задач
із використанням
технології “Що, якщо”
Розв'язування задач
із використанням
технології “Що, якщо”

Слайд #2
www.themegallery.com
Використання засобу Підбір параметра
У багатьох задачах певний результат є відомим, а от значення
параметрів, за яких цей результат досягається, - ні.
Приклад задачі
За якого обсягу випуску певної продукції фірма отримає прибуток у 100 000 гривень.
У математиці клас таких задач є найширшим. До нього відносяться задачі на розв'язання алгебраїчних рівнянь та нерівностей, пошук екстремумів функцій тощо.
Використання засобу Підбір параметра
У багатьох задачах певний результат є відомим, а от значення
параметрів, за яких цей результат досягається, - ні.
Приклад задачі
За якого обсягу випуску певної продукції фірма отримає прибуток у 100 000 гривень.
У математиці клас таких задач є найширшим. До нього відносяться задачі на розв'язання алгебраїчних рівнянь та нерівностей, пошук екстремумів функцій тощо.

Слайд #3
www.themegallery.com
Використання засобу Підбір параметра
У подібних задачах використовується поняття цільової функії.
Вона повинна досягти певного значення або оптимізуватися.
Цільова функція залежить від параметрів.
Задача знаходження певного значення цільової функції полягає у підборі таких значень параметрів, за яких цільова функція досягне необхідних значень
У MS Exsel є спеціальний засіб, який автоматично підбирає потрібні значення параметрів, знаходячи певне значення цільової функції. Він називається Підбір параметра.
Використання засобу Підбір параметра
У подібних задачах використовується поняття цільової функії.
Вона повинна досягти певного значення або оптимізуватися.
Цільова функція залежить від параметрів.
Задача знаходження певного значення цільової функції полягає у підборі таких значень параметрів, за яких цільова функція досягне необхідних значень
У MS Exsel є спеціальний засіб, який автоматично підбирає потрібні значення параметрів, знаходячи певне значення цільової функції. Він називається Підбір параметра.

Слайд #4
www.themegallery.com
Використання засобу Підбір параметра
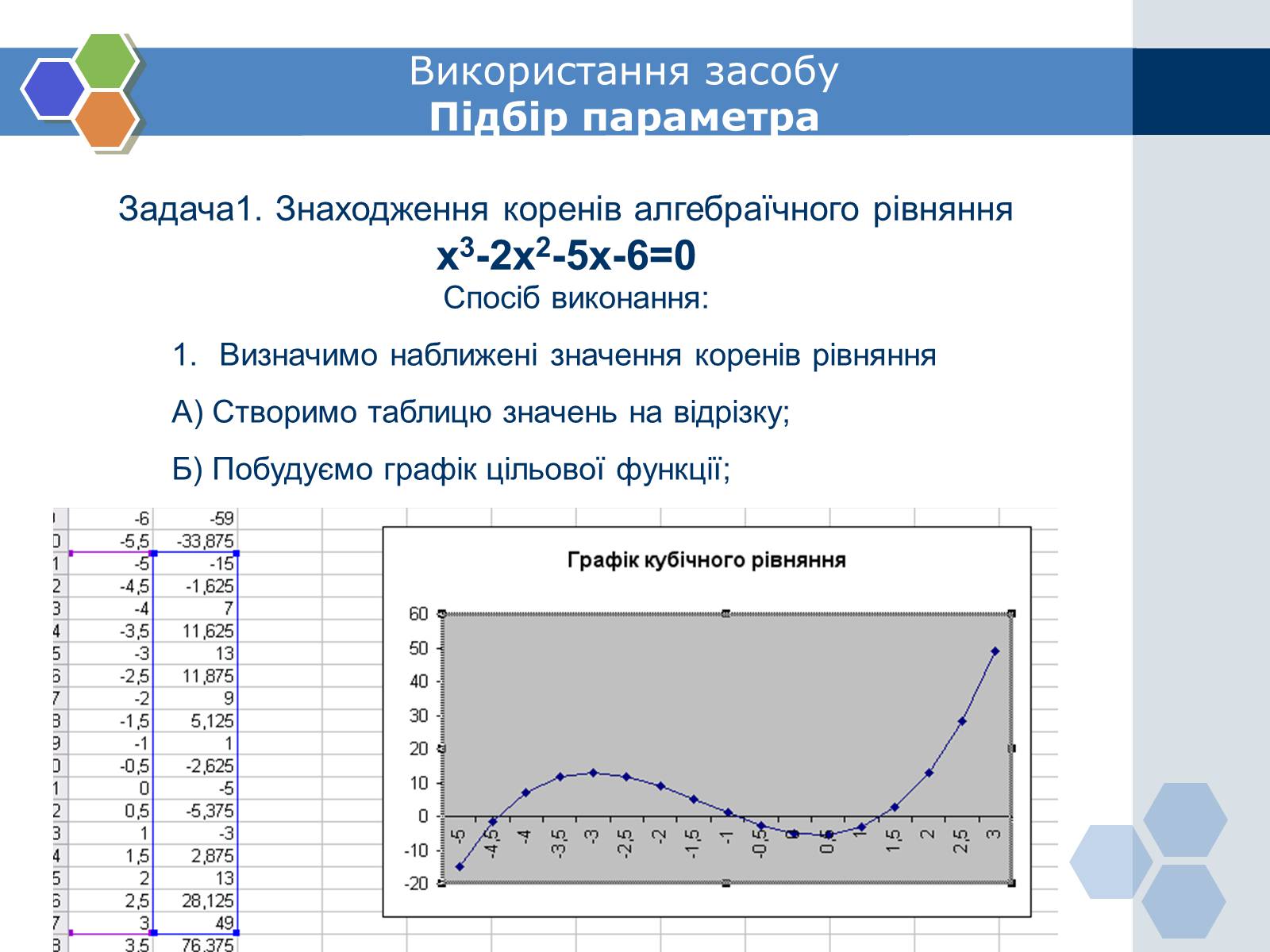
Задача1. Знаходження коренів алгебраїчного рівняння
x3-2x2-5x-6=0
Спосіб виконання:
Визначимо наближені значення коренів рівняння
А) Створимо таблицю значень на відрізку;
Б) Побудуємо графік цільової функції;
Використання засобу Підбір параметра
Задача1. Знаходження коренів алгебраїчного рівняння
x3-2x2-5x-6=0
Спосіб виконання:
Визначимо наближені значення коренів рівняння
А) Створимо таблицю значень на відрізку;
Б) Побудуємо графік цільової функції;
Слайд #5
www.themegallery.com
Використання засобу Підбір параметра
2. Клітинки В43:В45 будемо вважати цільовими и скопіюємо в них формулу;
3. У чарунки А43:А45 – приблизне значення коренів;
Використання засобу Підбір параметра
2. Клітинки В43:В45 будемо вважати цільовими и скопіюємо в них формулу;
3. У чарунки А43:А45 – приблизне значення коренів;

Слайд #6
www.themegallery.com
Використання засобу Підбір параметра
4. Викликати засіб Підбір параметру (Сервіс > Підбір параметру)
Заповнення вікна форми Підбір параметра
Результат обчислень
Використання засобу Підбір параметра
4. Викликати засіб Підбір параметру (Сервіс > Підбір параметру)
Заповнення вікна форми Підбір параметра
Результат обчислень

Слайд #7
www.themegallery.com
Використання засобу Підбір параметра
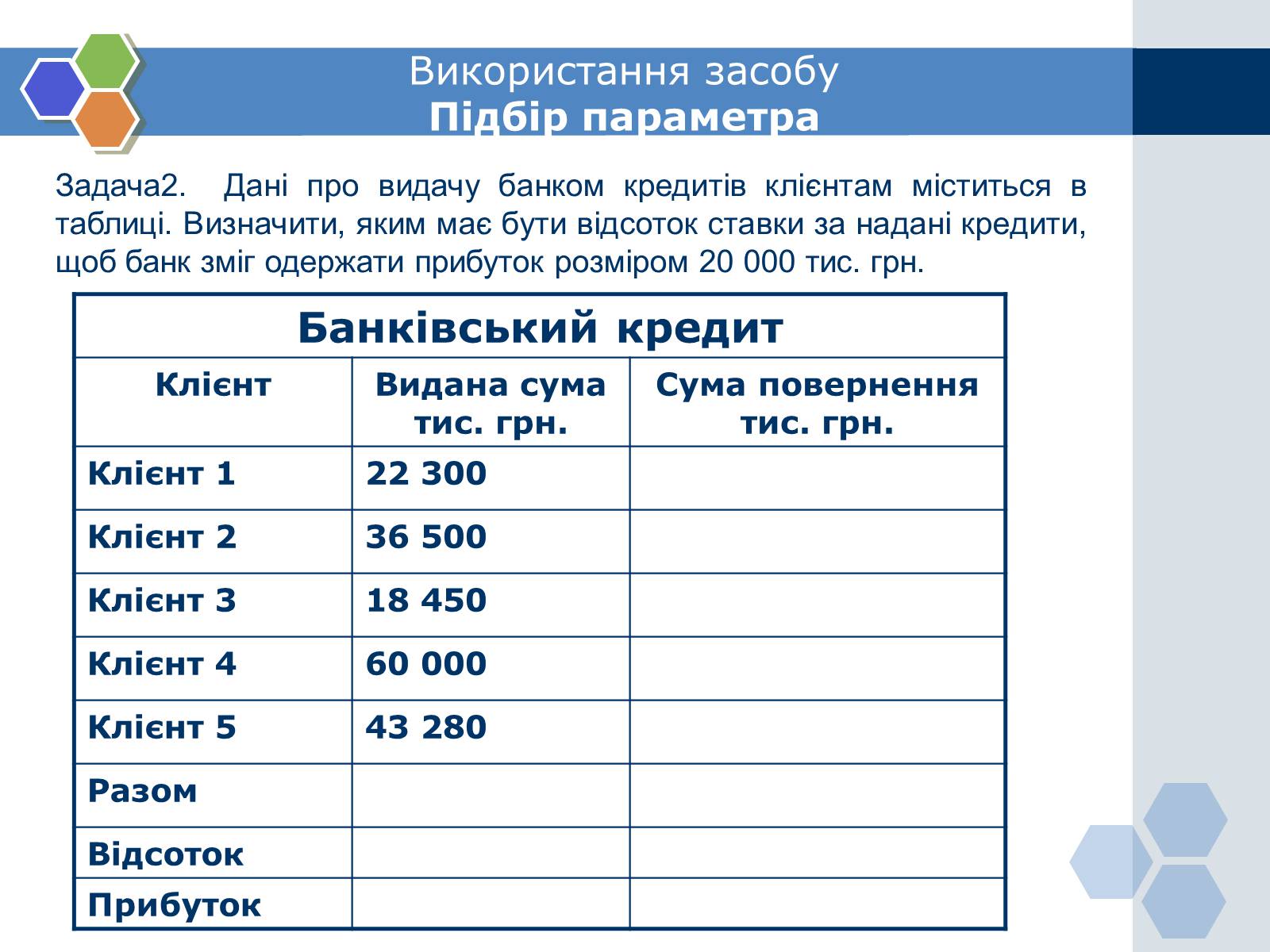
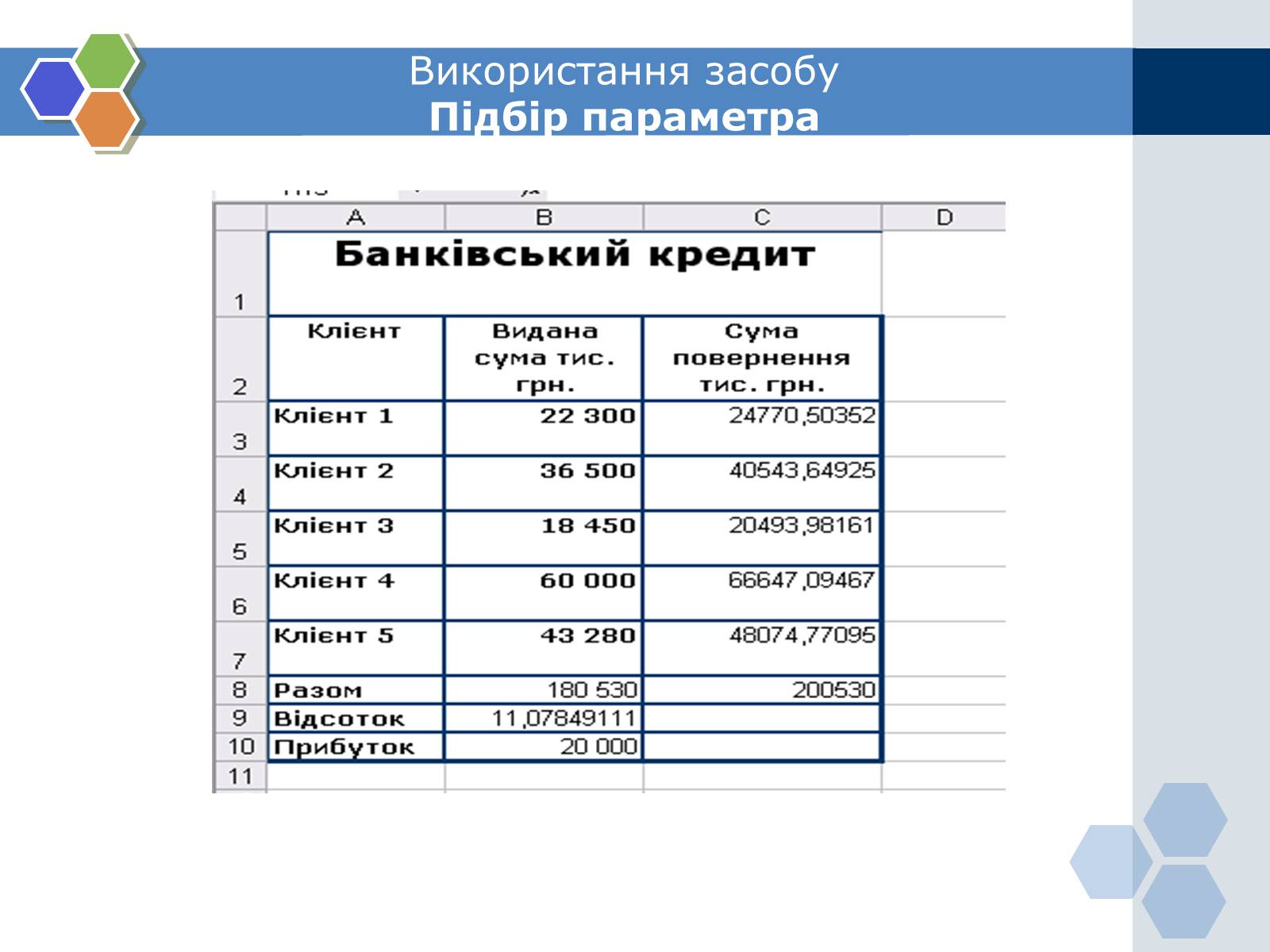
Задача2. Дані про видачу банком кредитів клієнтам міститься в таблиці. Визначити, яким має бути відсоток ставки за надані кредити, щоб банк зміг одержати прибуток розміром 20 000 тис. грн.
Банківський кредит
Клієнт
Видана сума тис. грн.
Сума повернення тис. грн.
Клієнт 1
22 300
Клієнт 2
36 500
Клієнт 3
18 450
Клієнт 4
60 000
Клієнт 5
43 280
Разом
Відсоток
Прибуток
Використання засобу Підбір параметра
Задача2. Дані про видачу банком кредитів клієнтам міститься в таблиці. Визначити, яким має бути відсоток ставки за надані кредити, щоб банк зміг одержати прибуток розміром 20 000 тис. грн.
Банківський кредит
Клієнт
Видана сума тис. грн.
Сума повернення тис. грн.
Клієнт 1
22 300
Клієнт 2
36 500
Клієнт 3
18 450
Клієнт 4
60 000
Клієнт 5
43 280
Разом
Відсоток
Прибуток
Слайд #8
www.themegallery.com
Використання засобу Підбір параметра
Використання засобу Підбір параметра
Слайд #9
www.themegallery.com
Використання засобу Підбір параметра
Задача 3. На деякому підприємстві випускається 1000 одиниць товару. Собівартість одиниці товару становить 10 грн., крім того фірма несе щомісячні витрати у розмірі 2000 грн., не пов'язані безпосередньо з виробництвом, та сплачує податок у розмірі 15% від доходу. Потрібно визначити, якою має бути ціна одиниці продукції, щоб підприємство отримувало щомісячний прибуток у розмірі 5000 грн. (припускається, що вся продукція продається).
Використання засобу Підбір параметра
Задача 3. На деякому підприємстві випускається 1000 одиниць товару. Собівартість одиниці товару становить 10 грн., крім того фірма несе щомісячні витрати у розмірі 2000 грн., не пов'язані безпосередньо з виробництвом, та сплачує податок у розмірі 15% від доходу. Потрібно визначити, якою має бути ціна одиниці продукції, щоб підприємство отримувало щомісячний прибуток у розмірі 5000 грн. (припускається, що вся продукція продається).

Слайд #10
www.themegallery.com
Використання засобу Пошук розв'язку
У багатьо задачах вимагається не просто знайти який-небудь розв'язок, а підібрати серед усіх розв'язків найкращій. Йдеться про задачі підбору збалансованого харчування, транспортні задачи та багато інших – їх ще називають задачами оптимізації.
Математична модель оптимізаційної задачі
Перш ніж розв'язувати задачу оптимізації її треба описати
у математичному вигляді, тобто побудувати її математичні модель.
Модель оптимізаційної задачі складається з елементів:
змінні – невідомі величини, значення яких необхідно знайти в
результаті розв'язання задачи;
цільова функція – величина, яка залежить від змінних і значення
якої потрібно максимізувати чи мінімізувати;
критерії – вимоги мінімізації чи максимізації цільової функції;
обмеження – умови, яким мають задовольняти змінні.
Використання засобу Пошук розв'язку
У багатьо задачах вимагається не просто знайти який-небудь розв'язок, а підібрати серед усіх розв'язків найкращій. Йдеться про задачі підбору збалансованого харчування, транспортні задачи та багато інших – їх ще називають задачами оптимізації.
Математична модель оптимізаційної задачі
Перш ніж розв'язувати задачу оптимізації її треба описати
у математичному вигляді, тобто побудувати її математичні модель.
Модель оптимізаційної задачі складається з елементів:
змінні – невідомі величини, значення яких необхідно знайти в
результаті розв'язання задачи;
цільова функція – величина, яка залежить від змінних і значення
якої потрібно максимізувати чи мінімізувати;
критерії – вимоги мінімізації чи максимізації цільової функції;
обмеження – умови, яким мають задовольняти змінні.

Слайд #11
www.themegallery.com
Використання засобу Пошук розв'язку
Алгоритм розв'язання задачі оптимізації
Введення позначень(яка змінна, яку величину позначає);
Створення цільової функції та критерію (визначити яка величина
буде максимізуватися або мінімізуватися, та записати формулу
залежності цієї величини від змінних;
3. Складання системи обмежень(нерівності або рівняння, яким мають задовольняти значення змінних);
4. Розв'язання задачі
Використання засобу Пошук розв'язку
Алгоритм розв'язання задачі оптимізації
Введення позначень(яка змінна, яку величину позначає);
Створення цільової функції та критерію (визначити яка величина
буде максимізуватися або мінімізуватися, та записати формулу
залежності цієї величини від змінних;
3. Складання системи обмежень(нерівності або рівняння, яким мають задовольняти значення змінних);
4. Розв'язання задачі

Слайд #12
www.themegallery.com
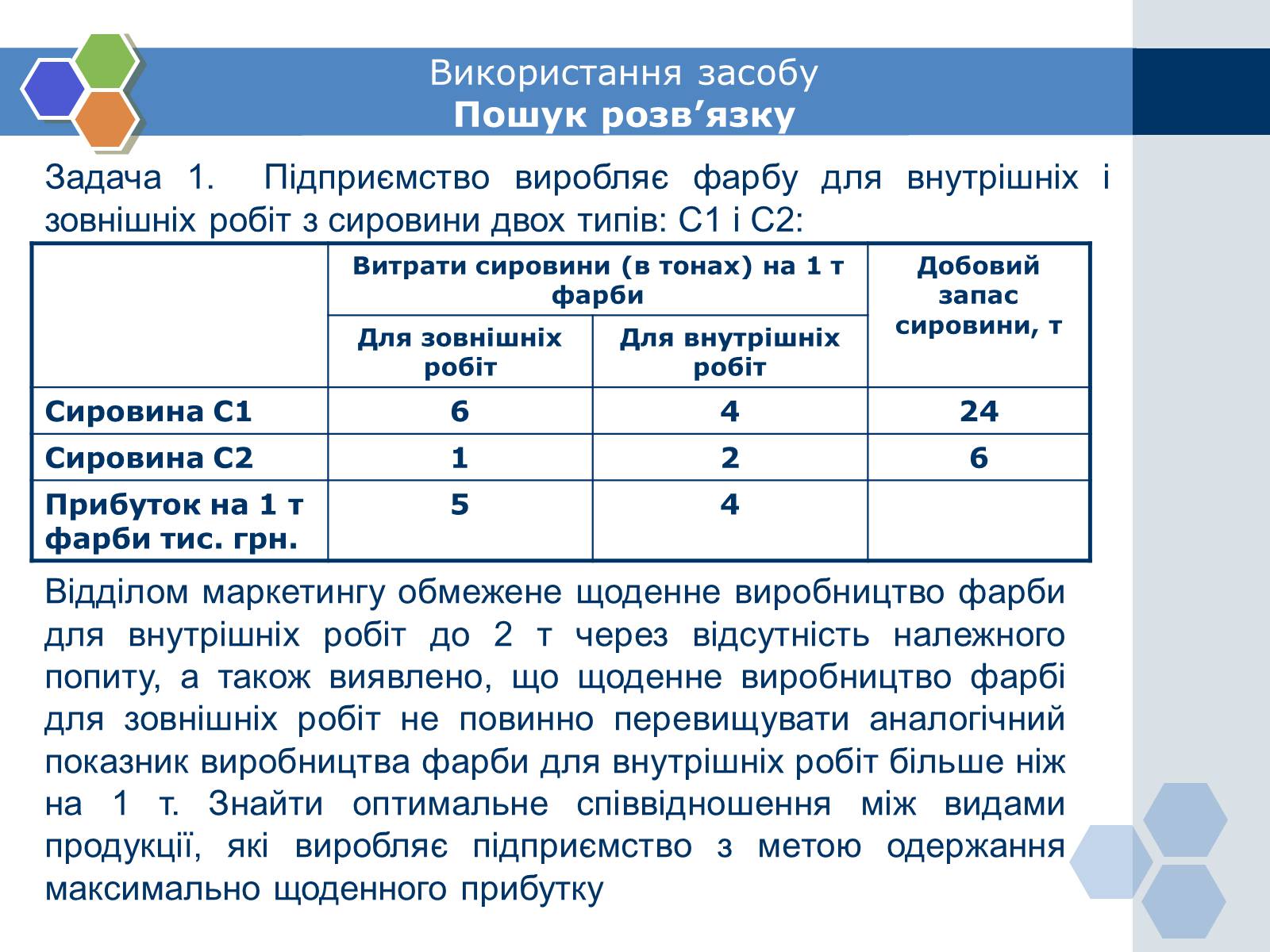
Задача 1. Підприємство виробляє фарбу для внутрішніх і зовнішніх робіт з сировини двох типів: С1 і С2:
Використання засобу Пошук розв'язку
Витрати сировини (в тонах) на 1 т фарби
Добовий запас сировини, т
Для зовнішніх робіт
Для внутрішніх робіт
Сировина С1
6
4
24
Сировина С2
1
2
6
Прибуток на 1 т фарби тис. грн.
5
4
Відділом маркетингу обмежене щоденне виробництво фарби для внутрішніх робіт до 2 т через відсутність належного попиту, а також виявлено, що щоденне виробництво фарбі для зовнішніх робіт не повинно перевищувати аналогічний показник виробництва фарби для внутрішніх робіт більше ніж на 1 т. Знайти оптимальне співвідношення між видами продукції, які виробляє підприємство з метою одержання максимально щоденного прибутку
Задача 1. Підприємство виробляє фарбу для внутрішніх і зовнішніх робіт з сировини двох типів: С1 і С2:
Використання засобу Пошук розв'язку
Витрати сировини (в тонах) на 1 т фарби
Добовий запас сировини, т
Для зовнішніх робіт
Для внутрішніх робіт
Сировина С1
6
4
24
Сировина С2
1
2
6
Прибуток на 1 т фарби тис. грн.
5
4
Відділом маркетингу обмежене щоденне виробництво фарби для внутрішніх робіт до 2 т через відсутність належного попиту, а також виявлено, що щоденне виробництво фарбі для зовнішніх робіт не повинно перевищувати аналогічний показник виробництва фарби для внутрішніх робіт більше ніж на 1 т. Знайти оптимальне співвідношення між видами продукції, які виробляє підприємство з метою одержання максимально щоденного прибутку
Слайд #13
www.themegallery.com
Використання засобу Пошук розв'язку
1. Створюємо ЕТ
Використання засобу Пошук розв'язку
1. Створюємо ЕТ

Слайд #14
www.themegallery.com
Використання засобу Пошук розв'язку
2. Обчислюємо значення в чарунках Е3, Е4
Використання засобу Пошук розв'язку
2. Обчислюємо значення в чарунках Е3, Е4

Слайд #15
www.themegallery.com
Використання засобу Пошук розв'язку
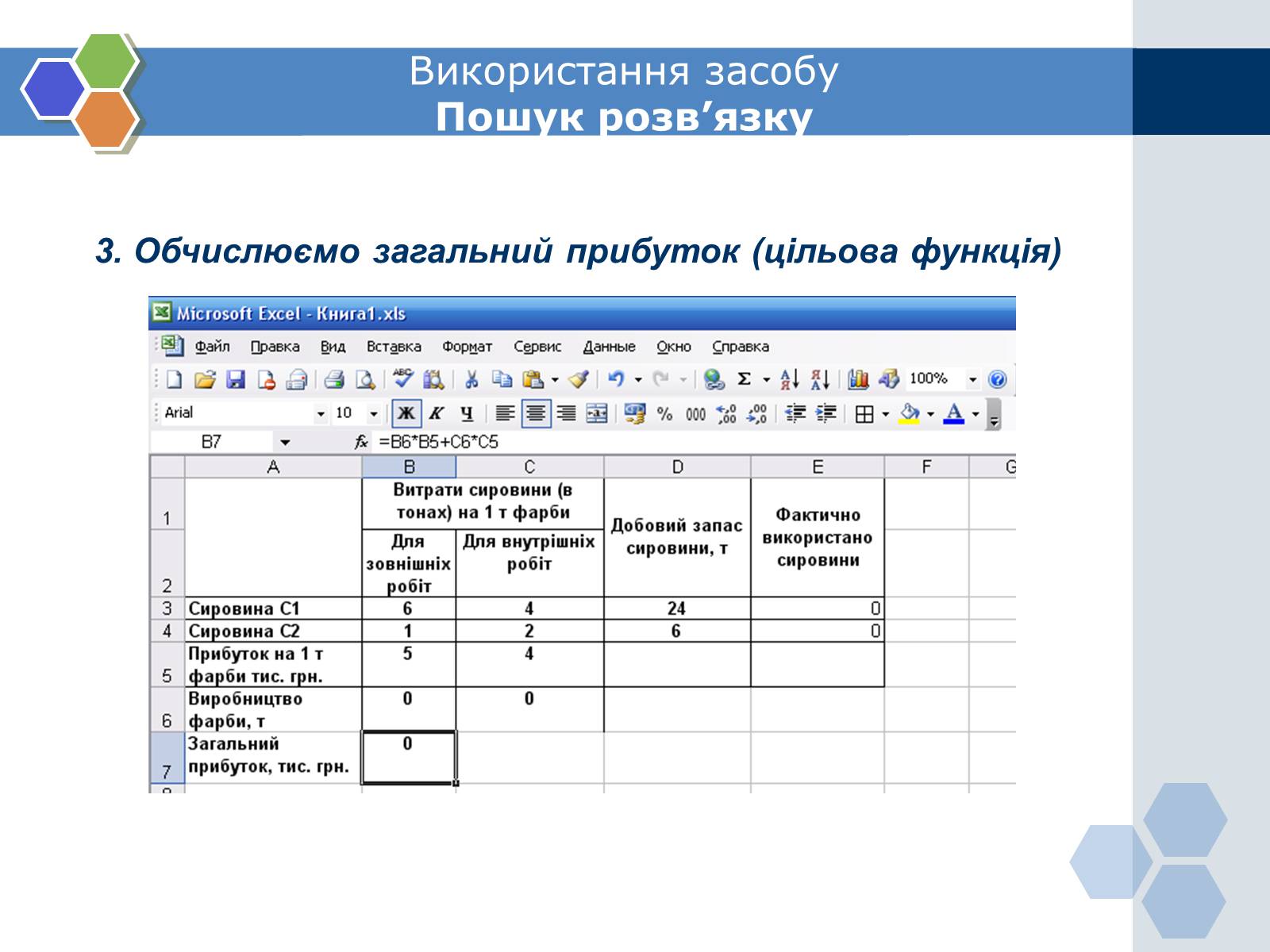
3. Обчислюємо загальний прибуток (цільова функція)
Використання засобу Пошук розв'язку
3. Обчислюємо загальний прибуток (цільова функція)
Слайд #16
www.themegallery.com
Використання засобу Пошук розв'язку
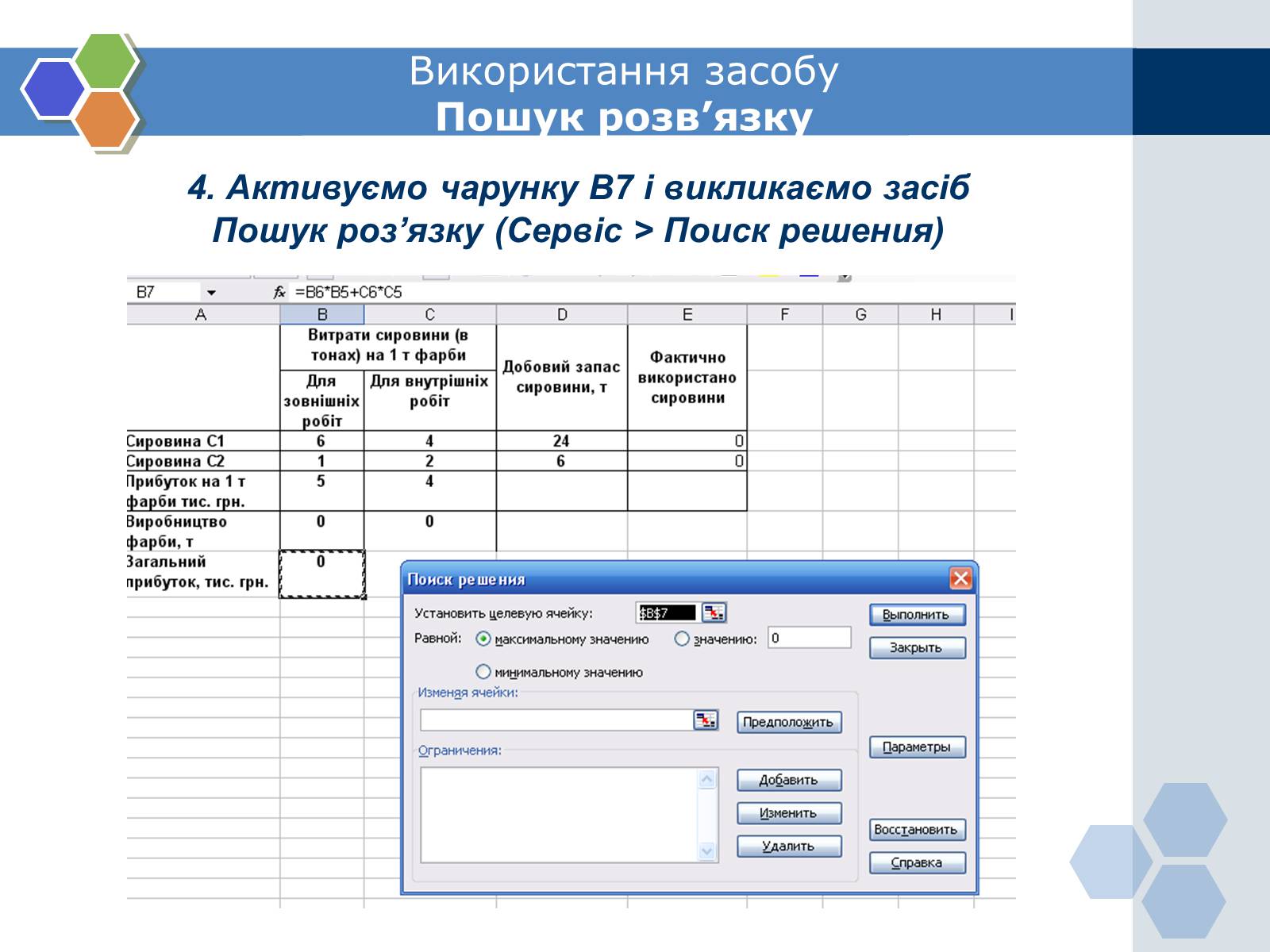
4. Активуємо чарунку В7 і викликаємо засіб
Пошук роз'язку (Сервіс > Поиск решения)
Використання засобу Пошук розв'язку
4. Активуємо чарунку В7 і викликаємо засіб
Пошук роз'язку (Сервіс > Поиск решения)
Слайд #17
www.themegallery.com
Використання засобу Пошук розв'язку
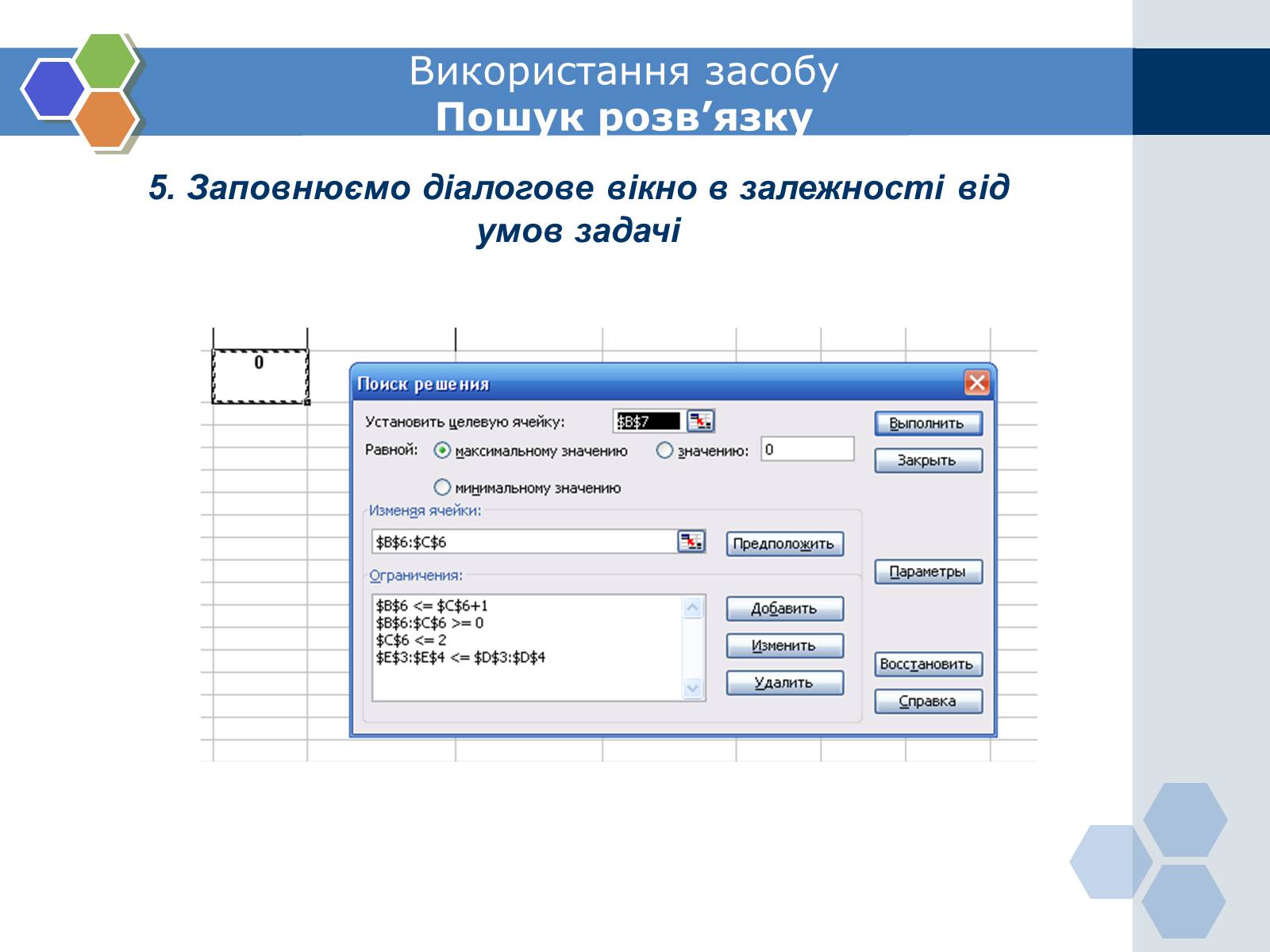
5. Заповнюємо діалогове вікно в залежності від
умов задачі
Використання засобу Пошук розв'язку
5. Заповнюємо діалогове вікно в залежності від
умов задачі
Слайд #18
www.themegallery.com
Використання засобу Пошук розв'язку
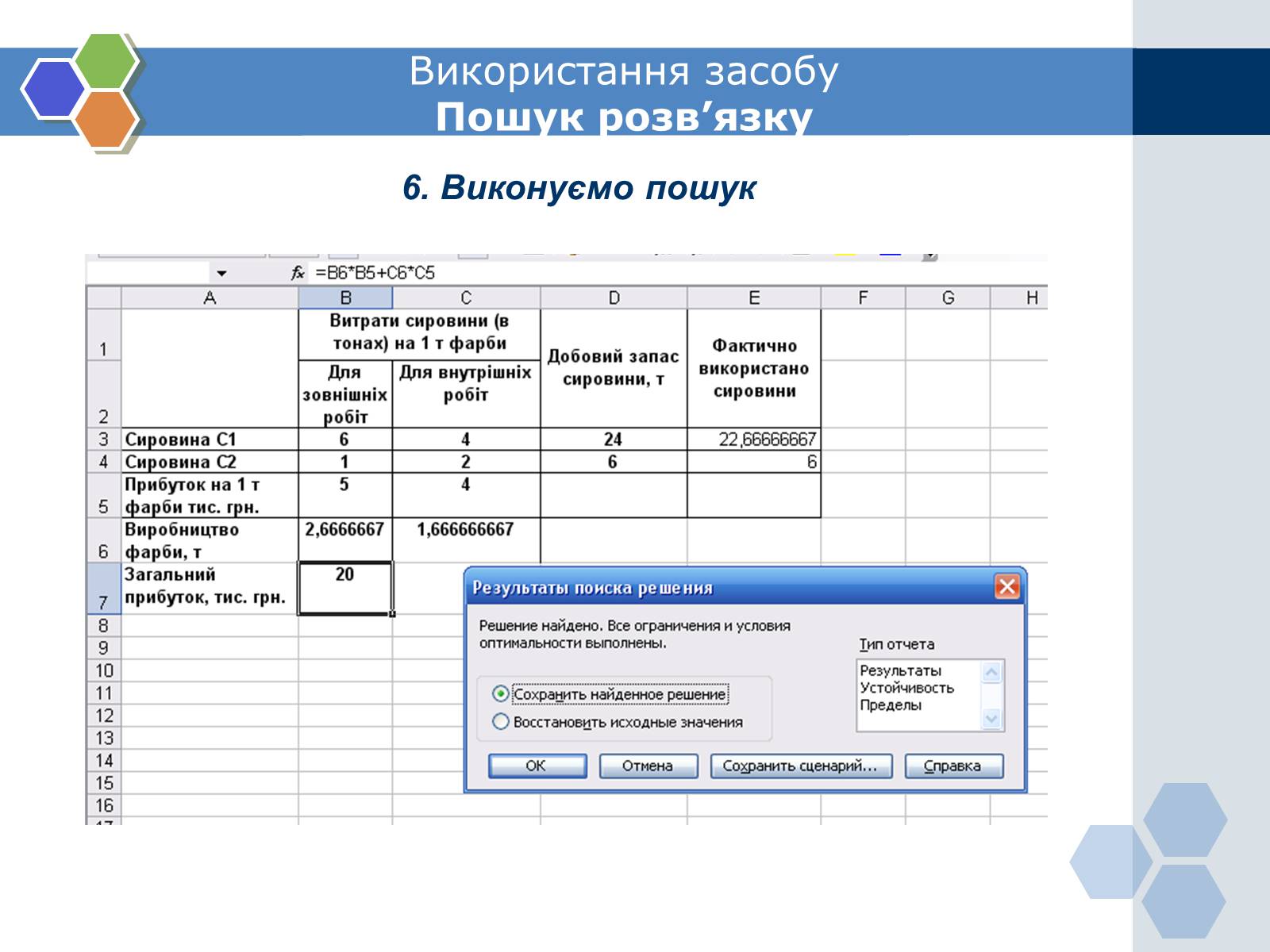
6. Виконуємо пошук
Використання засобу Пошук розв'язку
6. Виконуємо пошук
Слайд #19
www.themegallery.com
Використання засобу Пошук розв'язку
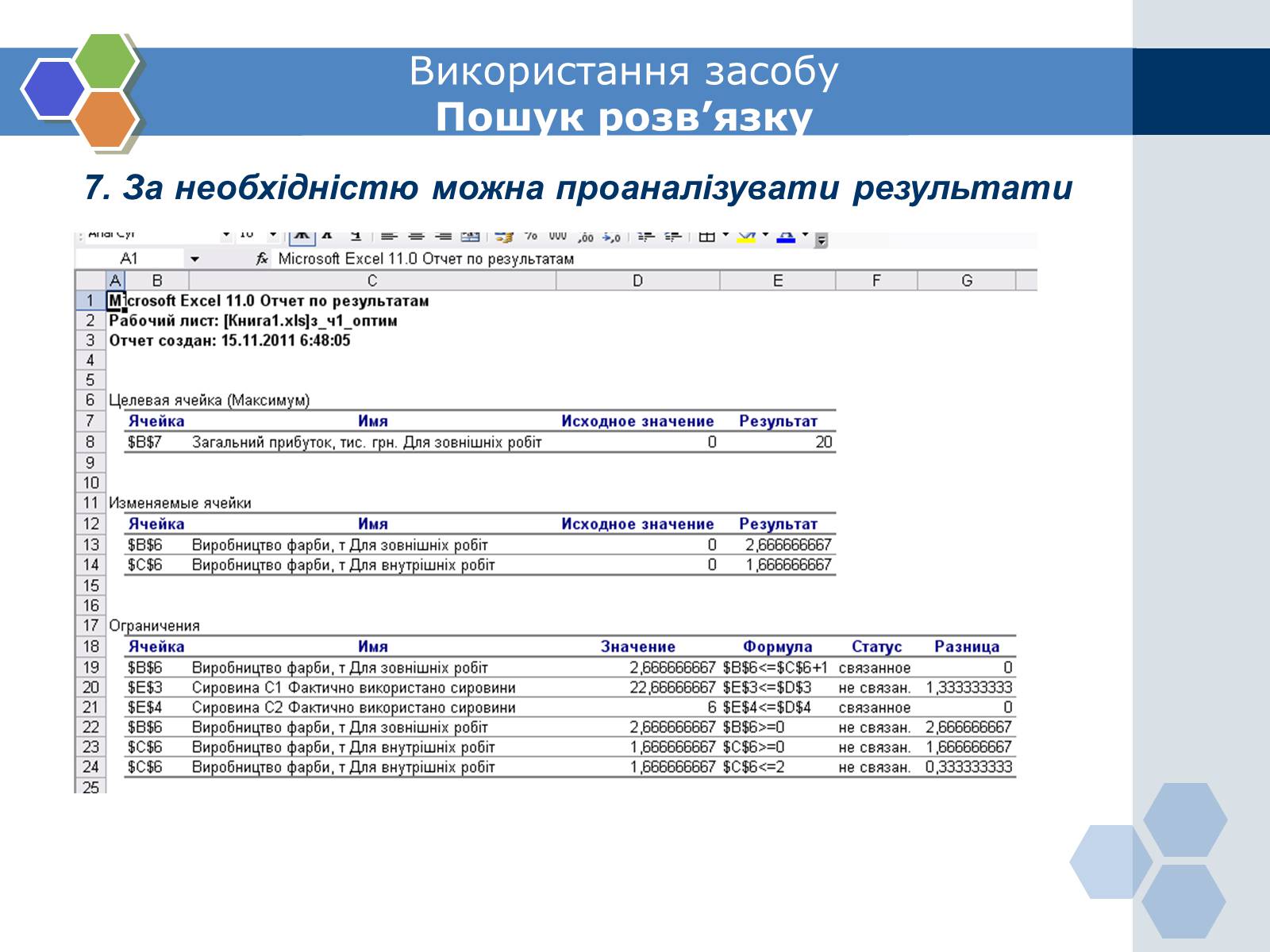
7. За необхідністю можна проаналізувати результати
Використання засобу Пошук розв'язку
7. За необхідністю можна проаналізувати результати
Слайд #20
www.themegallery.com
Використання засобу Пошук розв'язку
Вид інградієнта
Страва А
Страва Б
Страва В
Інгредієнт 1
10
50
10
Інгредієнт 2
20
40
Інгредієнт 3
20
10
30
Інгредієнт 4
30
15
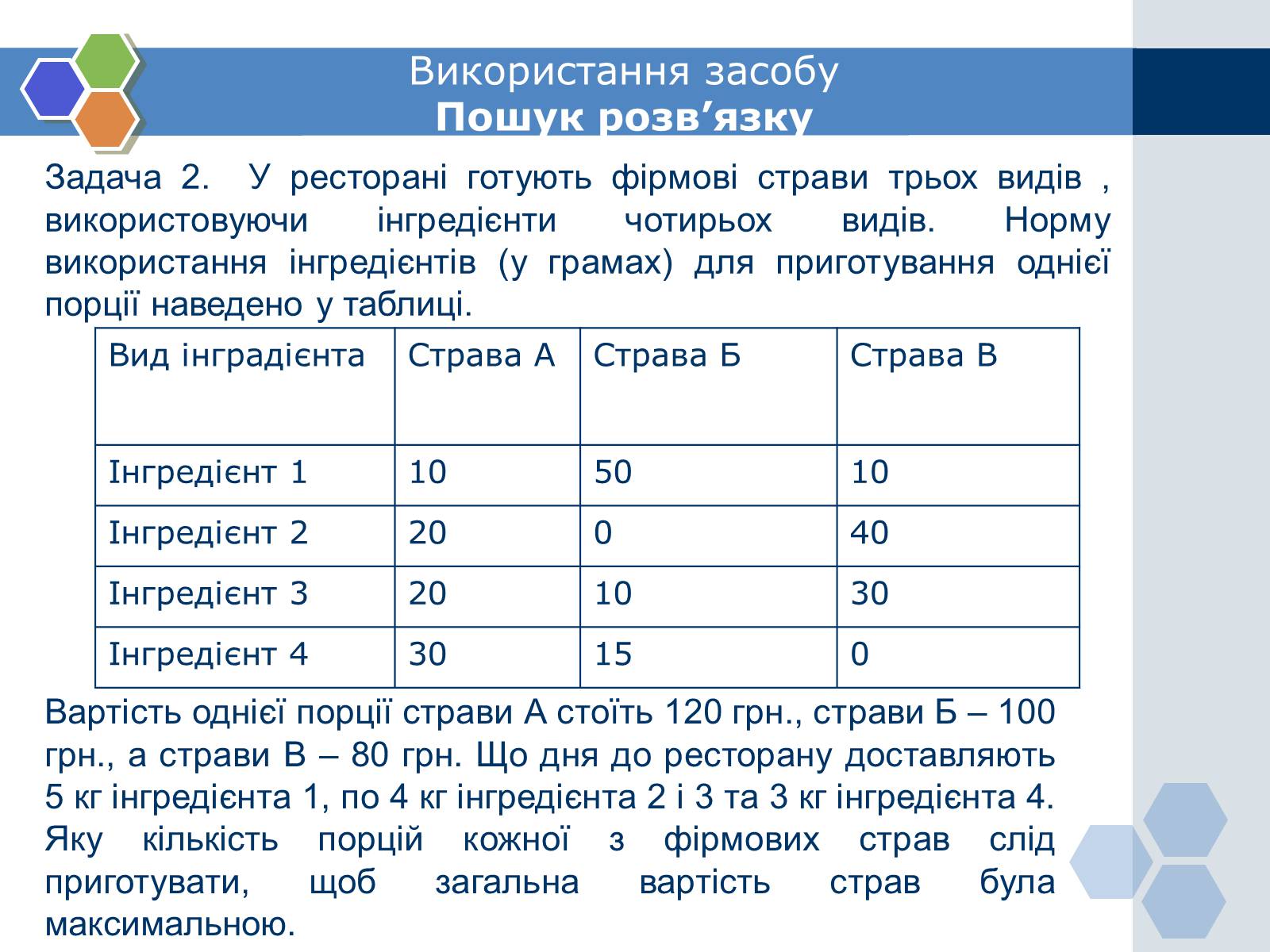
Задача 2. У ресторані готують фірмові страви трьох видів , використовуючи інгредієнти чотирьох видів. Норму використання інгредієнтів (у грамах) для приготування однієї порції наведено у таблиці.
Вартість однієї порції страви А стоїть 120 грн., страви Б – 100 грн., а страви В – 80 грн. Що дня до ресторану доставляють 5 кг інгредієнта 1, по 4 кг інгредієнта 2 і 3 та 3 кг інгредієнта 4. Яку кількість порцій кожної з фірмових страв слід приготувати, щоб загальна вартість страв була максимальною.
Використання засобу Пошук розв'язку
Вид інградієнта
Страва А
Страва Б
Страва В
Інгредієнт 1
10
50
10
Інгредієнт 2
20
40
Інгредієнт 3
20
10
30
Інгредієнт 4
30
15
Задача 2. У ресторані готують фірмові страви трьох видів , використовуючи інгредієнти чотирьох видів. Норму використання інгредієнтів (у грамах) для приготування однієї порції наведено у таблиці.
Вартість однієї порції страви А стоїть 120 грн., страви Б – 100 грн., а страви В – 80 грн. Що дня до ресторану доставляють 5 кг інгредієнта 1, по 4 кг інгредієнта 2 і 3 та 3 кг інгредієнта 4. Яку кількість порцій кожної з фірмових страв слід приготувати, щоб загальна вартість страв була максимальною.
Слайд #21
www.themegallery.com
Використання засобу Пошук розв'язку
Математична модель
Введемо позначення х1 – кількість порцій страви А, х2 – кількість порцій страви – Б, х3 – кількість порцій страви В.
Загальна вартість страв визначається за формулою 120х1+100х2+80х3 – формула цільової функції.
З таблиці випливають умови:
20х1+50х2+10х3<=5000 (Інгредієнт 1)
20х1+40х2<=4000 (Інгредієнт 2)
20х1+10х2+30х3<=4000 (Інгредієнт 3)
30х1+15х2<=3000 (Інгредієнт 4)
х1, х2, х3 – цілі числа
x1>=0, x2>=0, x3>=0
Використання засобу Пошук розв'язку
Математична модель
Введемо позначення х1 – кількість порцій страви А, х2 – кількість порцій страви – Б, х3 – кількість порцій страви В.
Загальна вартість страв визначається за формулою 120х1+100х2+80х3 – формула цільової функції.
З таблиці випливають умови:
20х1+50х2+10х3<=5000 (Інгредієнт 1)
20х1+40х2<=4000 (Інгредієнт 2)
20х1+10х2+30х3<=4000 (Інгредієнт 3)
30х1+15х2<=3000 (Інгредієнт 4)
х1, х2, х3 – цілі числа
x1>=0, x2>=0, x3>=0

Слайд #22
www.themegallery.com
Використання засобу Пошук розв'язку
Задача 3. У зоопарку використовують два види кормів: 100 г першого корму містить 2 г білків, 6 г жирів, 4 г вуглеводів і коштує 5 грн; 100 г другого корму містить 3 г білків, 2 г жирів, 9 г вуглеводів і коштує 4 грн. Потрібно скласти раціон харчування тварини в зоопарку за умови, що вона має щодня отримувати не менше 60 г білків, 80 г жирів і 150 г вуглеводів, а вартість добової норми їжі повинна бути мінімальною.
Використання засобу Пошук розв'язку
Задача 3. У зоопарку використовують два види кормів: 100 г першого корму містить 2 г білків, 6 г жирів, 4 г вуглеводів і коштує 5 грн; 100 г другого корму містить 3 г білків, 2 г жирів, 9 г вуглеводів і коштує 4 грн. Потрібно скласти раціон харчування тварини в зоопарку за умови, що вона має щодня отримувати не менше 60 г білків, 80 г жирів і 150 г вуглеводів, а вартість добової норми їжі повинна бути мінімальною.
