- Головна
- Готові шкільні презентації
- Презентація на тему «Геометрія для 8 класу»
Презентація на тему «Геометрія для 8 класу»
1303
Слайд #1
Геометрія 8 клас

Слайд #2
Паралелограм та його властивості
Трапеція та її властивості
Теорема Фалеса.
Середня лінія трикутника і трапеції
Теорема Піфагора.
Розв'язування прямокутних трикутників
Узагальнена теорема Фалеса.
Подібність трикутників
Чотирикутники
Трапеція та її властивості
Теорема Фалеса.
Середня лінія трикутника і трапеції
Теорема Піфагора.
Розв'язування прямокутних трикутників
Узагальнена теорема Фалеса.
Подібність трикутників
Чотирикутники

Слайд #3
Чотирикутники
Чотирикутники – багатокутники, які мають
чотири вершини і чотири сторони.
Чотирикутники можуть бути опуклими та неопуклими
ABCD – опуклий чотирикутник
FRLK – неопуклий чотирикутник .
Чотирикутники – багатокутники, які мають
чотири вершини і чотири сторони.
Чотирикутники можуть бути опуклими та неопуклими
ABCD – опуклий чотирикутник
FRLK – неопуклий чотирикутник .

Слайд #4
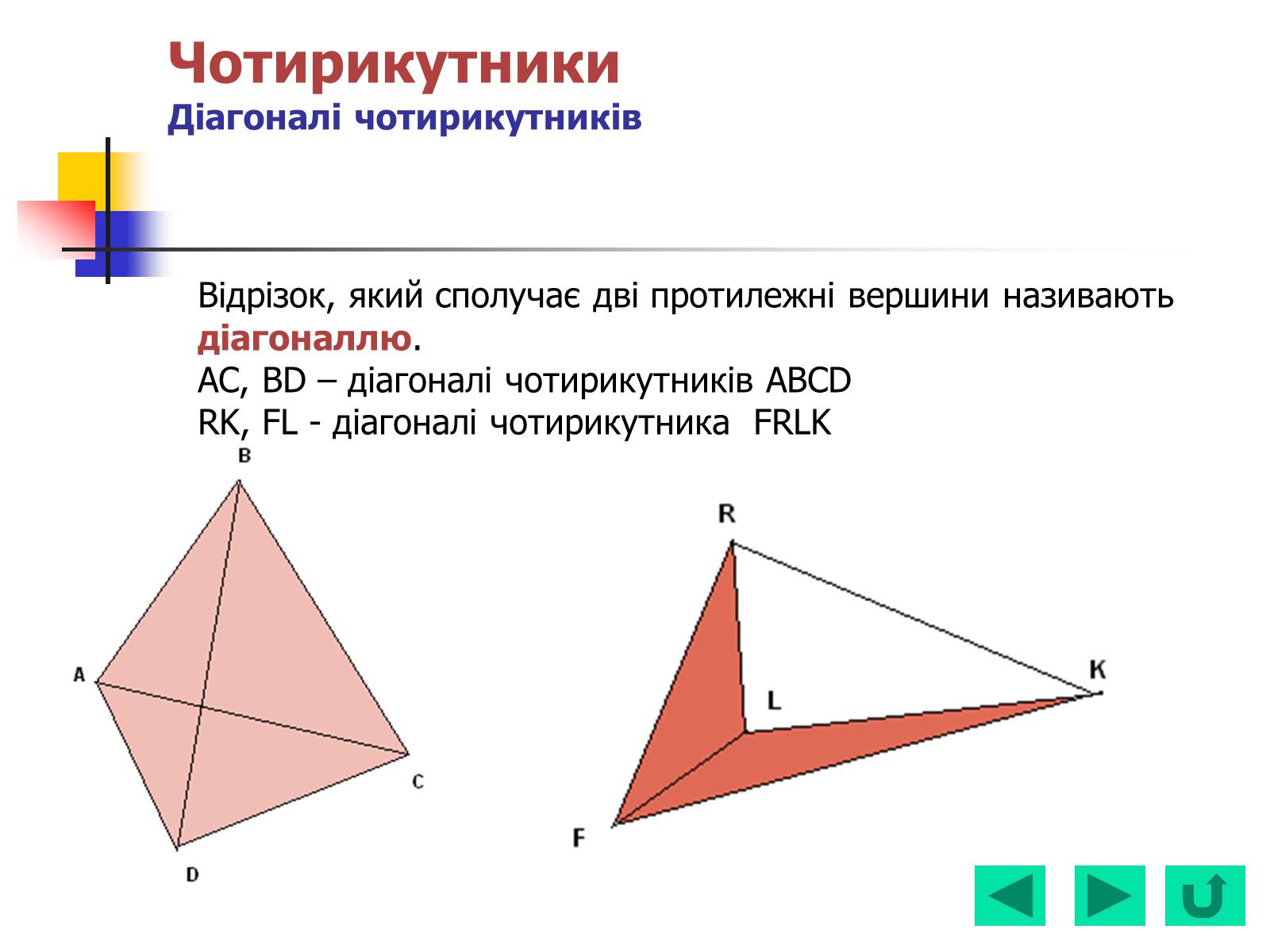
Відрізок, який сполучає дві протилежні вершини називають діагоналлю.
AC, BD – діагоналі чотирикутників ABCD
RK, FL - діагоналі чотирикутника FRLK
ЧотирикутникиДіагоналі чотирикутників
AC, BD – діагоналі чотирикутників ABCD
RK, FL - діагоналі чотирикутника FRLK
ЧотирикутникиДіагоналі чотирикутників
Слайд #5
ЧотирикутникиВластивості кутів опуклого чотирикутника
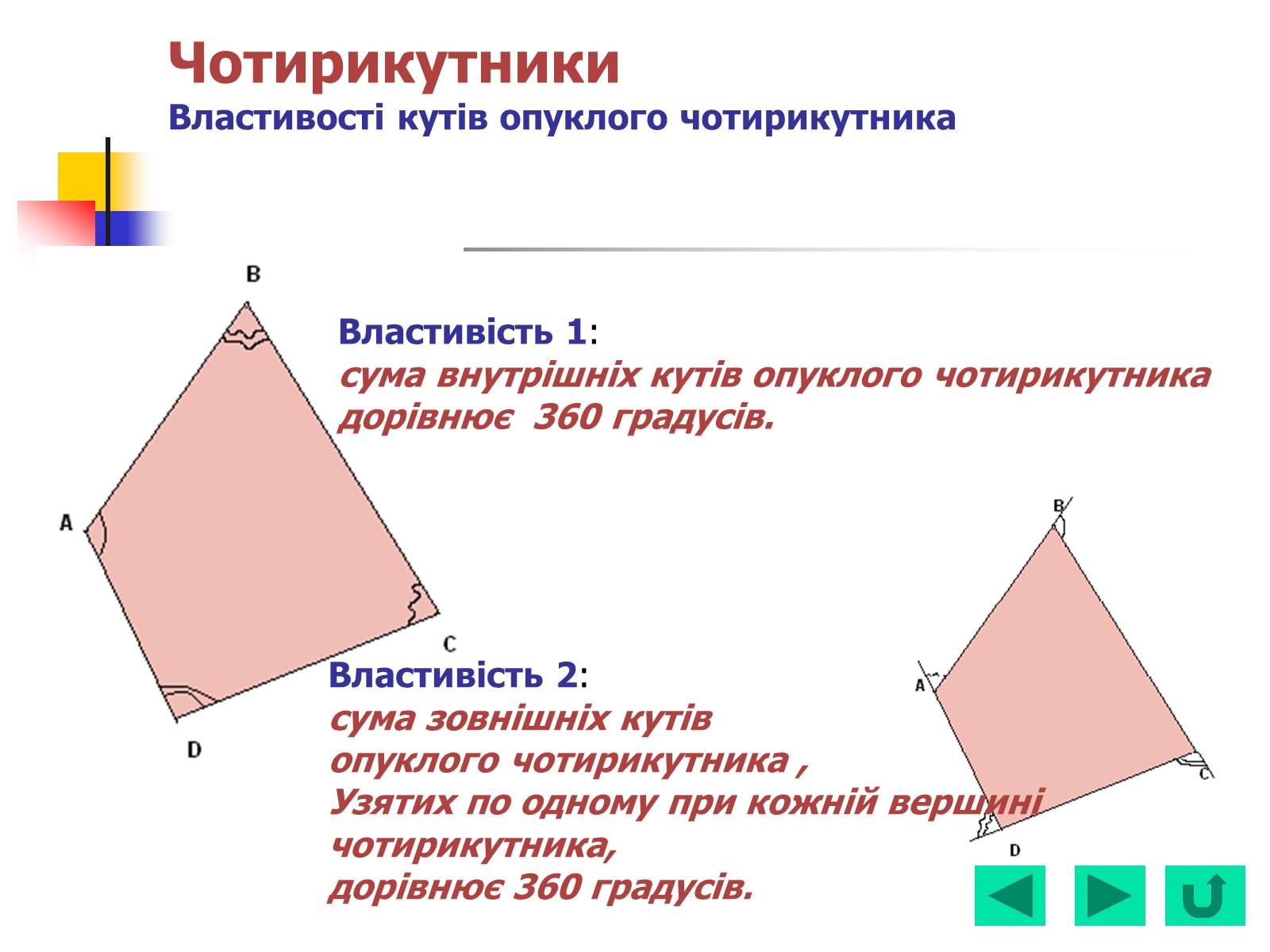
Властивість 1:
сума внутрішніх кутів опуклого чотирикутника
дорівнює 360 градусів.
Властивість 2:
сума зовнішніх кутів
опуклого чотирикутника ,
Узятих по одному при кожній вершині чотирикутника,
дорівнює 360 градусів.
Властивість 1:
сума внутрішніх кутів опуклого чотирикутника
дорівнює 360 градусів.
Властивість 2:
сума зовнішніх кутів
опуклого чотирикутника ,
Узятих по одному при кожній вершині чотирикутника,
дорівнює 360 градусів.
Слайд #6
ЧотирикутникиВластивість сторін опуклого чотирикутника
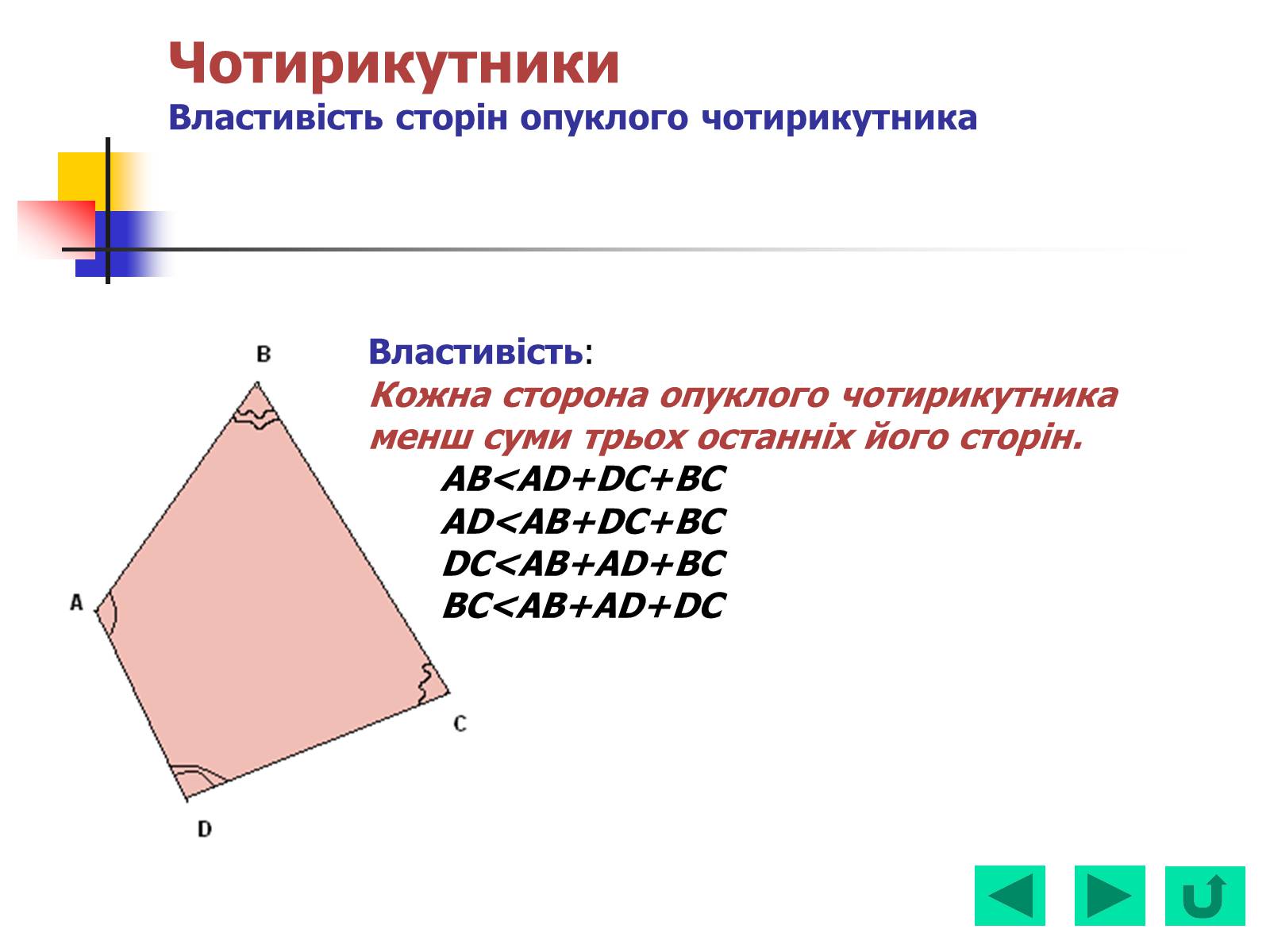
Властивість:
Кожна сторона опуклого чотирикутника
менш суми трьох останніх його сторін.
ABADDCBC
Властивість:
Кожна сторона опуклого чотирикутника
менш суми трьох останніх його сторін.
AB
Слайд #7
Чотирикутники Вписані чотирикутники
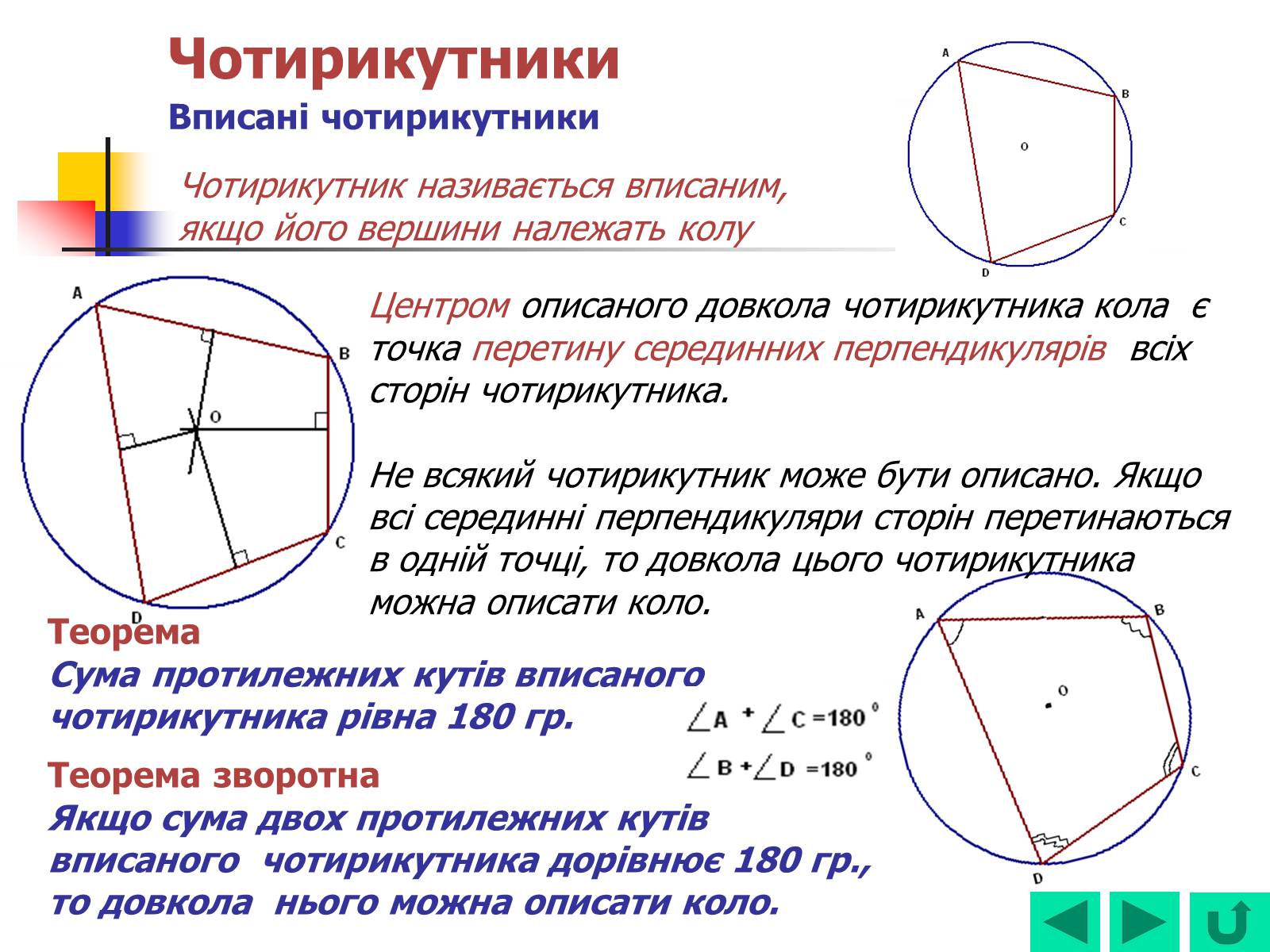
Чотирикутник називається вписаним, якщо його вершини належать колу
Центром описаного довкола чотирикутника кола є точка перетину серединних перпендикулярів всіх сторін чотирикутника.
Не всякий чотирикутник може бути описано. Якщо всі серединні перпендикуляри сторін перетинаються в одній точці, то довкола цього чотирикутника можна описати коло.
Теорема
Сума протилежних кутів вписаного
чотирикутника рівна 180 гр.
Теорема зворотна
Якщо сума двох протилежних кутів вписаного чотирикутника дорівнює 180 гр., то довкола нього можна описати коло.
Чотирикутник називається вписаним, якщо його вершини належать колу
Центром описаного довкола чотирикутника кола є точка перетину серединних перпендикулярів всіх сторін чотирикутника.
Не всякий чотирикутник може бути описано. Якщо всі серединні перпендикуляри сторін перетинаються в одній точці, то довкола цього чотирикутника можна описати коло.
Теорема
Сума протилежних кутів вписаного
чотирикутника рівна 180 гр.
Теорема зворотна
Якщо сума двох протилежних кутів вписаного чотирикутника дорівнює 180 гр., то довкола нього можна описати коло.
Слайд #8
Чотирикутники Описані чотирикутники
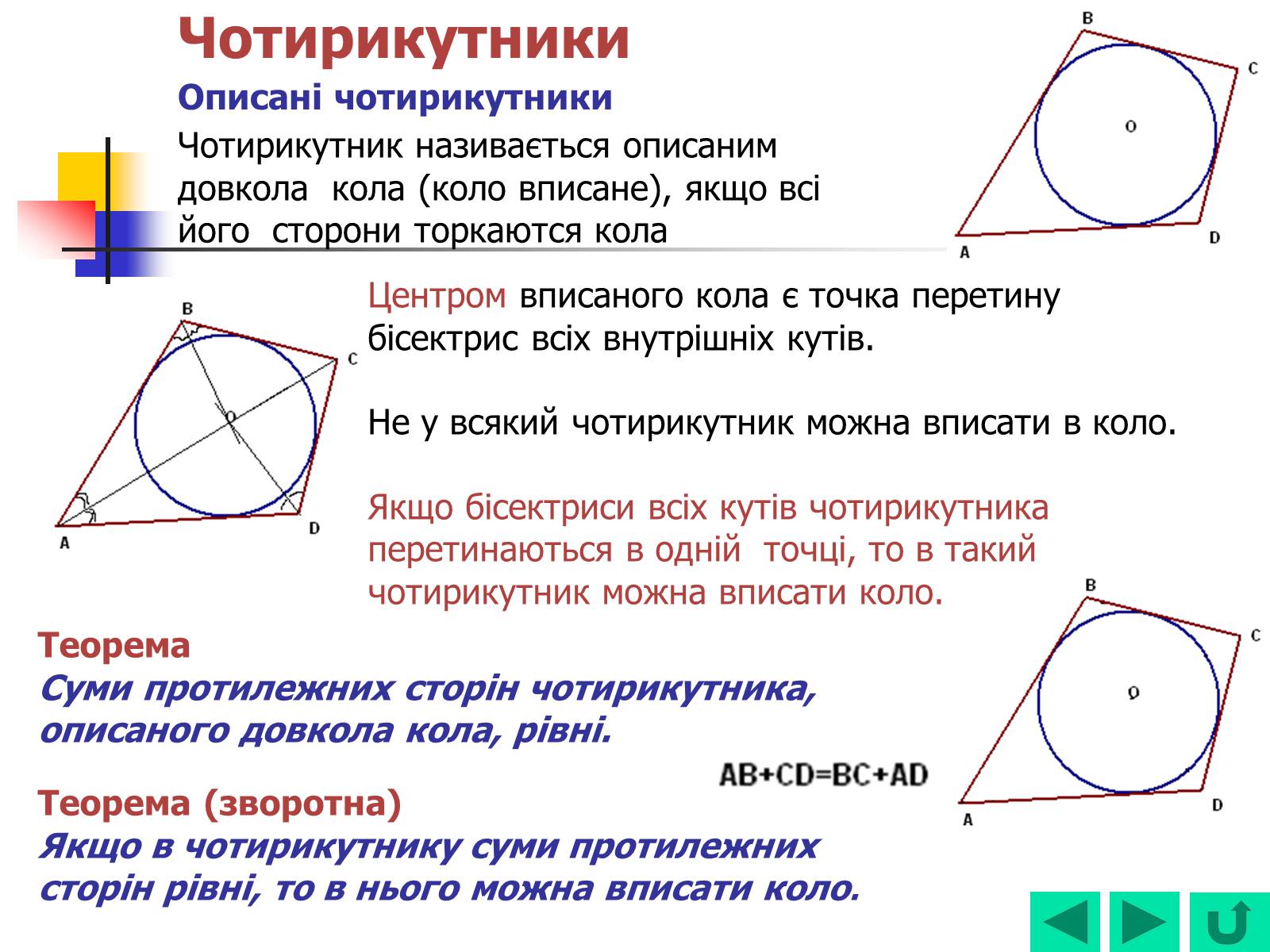
Чотирикутник називається описаним довкола кола (коло вписане), якщо всі його сторони торкаются кола
Центром вписаного кола є точка перетину бісектрис всіх внутрішніх кутів.
Не у всякий чотирикутник можна вписати в коло.
Якщо бісектриси всіх кутів чотирикутника перетинаються в одній точці, то в такий чотирикутник можна вписати коло.
Теорема
Суми протилежних сторін чотирикутника, описаного довкола кола, рівні.
Теорема (зворотна)
Якщо в чотирикутнику суми протилежних сторін рівні, то в нього можна вписати коло.
Чотирикутник називається описаним довкола кола (коло вписане), якщо всі його сторони торкаются кола
Центром вписаного кола є точка перетину бісектрис всіх внутрішніх кутів.
Не у всякий чотирикутник можна вписати в коло.
Якщо бісектриси всіх кутів чотирикутника перетинаються в одній точці, то в такий чотирикутник можна вписати коло.
Теорема
Суми протилежних сторін чотирикутника, описаного довкола кола, рівні.
Теорема (зворотна)
Якщо в чотирикутнику суми протилежних сторін рівні, то в нього можна вписати коло.
Слайд #9
ЧотирикутникиВіди чотирикутників
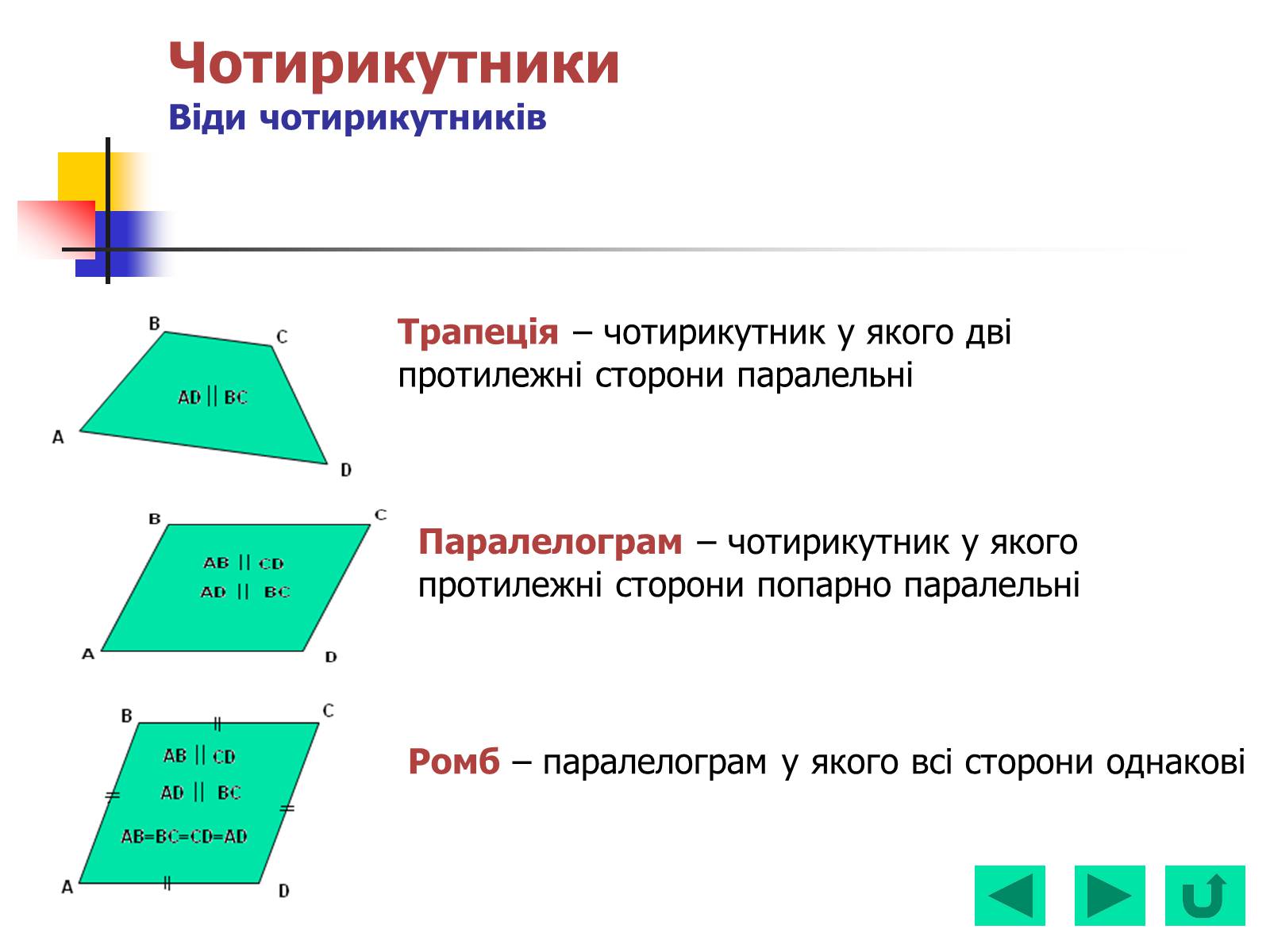
Трапеція – чотирикутник у якого дві
протилежні сторони паралельні
Паралелограм – чотирикутник у якого
протилежні сторони попарно паралельні
Ромб – паралелограм у якого всі сторони однакові
Трапеція – чотирикутник у якого дві
протилежні сторони паралельні
Паралелограм – чотирикутник у якого
протилежні сторони попарно паралельні
Ромб – паралелограм у якого всі сторони однакові
Слайд #10
ЧотирикутникиВиди чотирикутників
Прямокутник – паралелограм, у якого
всі кути прямі
Квадрат – прямокутник, у якого
всі сторони однакові
Прямокутник – паралелограм, у якого
всі кути прямі
Квадрат – прямокутник, у якого
всі сторони однакові

Слайд #11
Чотирикутники
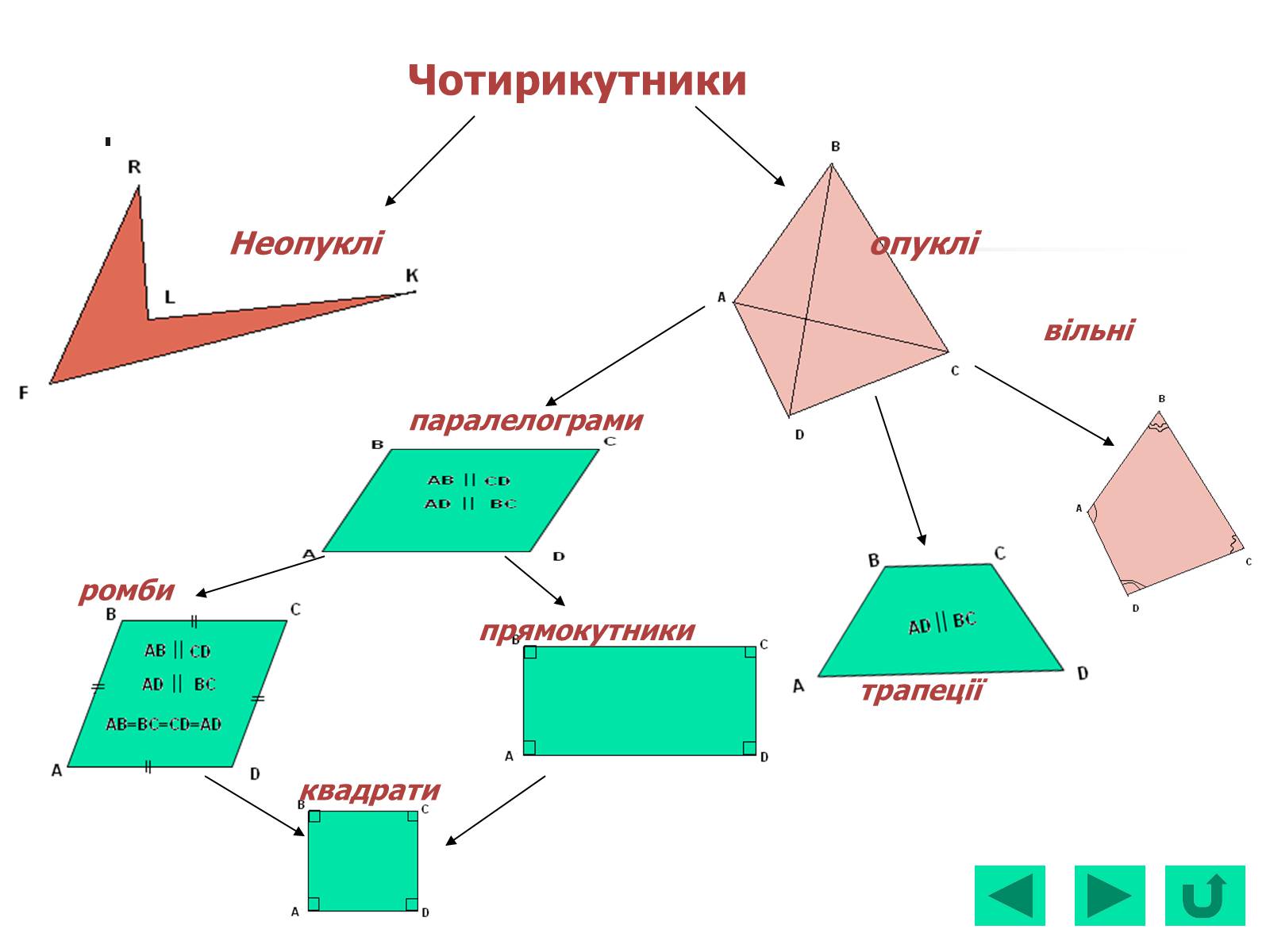
опуклі
Неопуклі
вільні
трапеції
паралелограми
ромби
прямокутники
квадрати
опуклі
Неопуклі
вільні
трапеції
паралелограми
ромби
прямокутники
квадрати
Слайд #12
ЧотирикутникиЗавдання
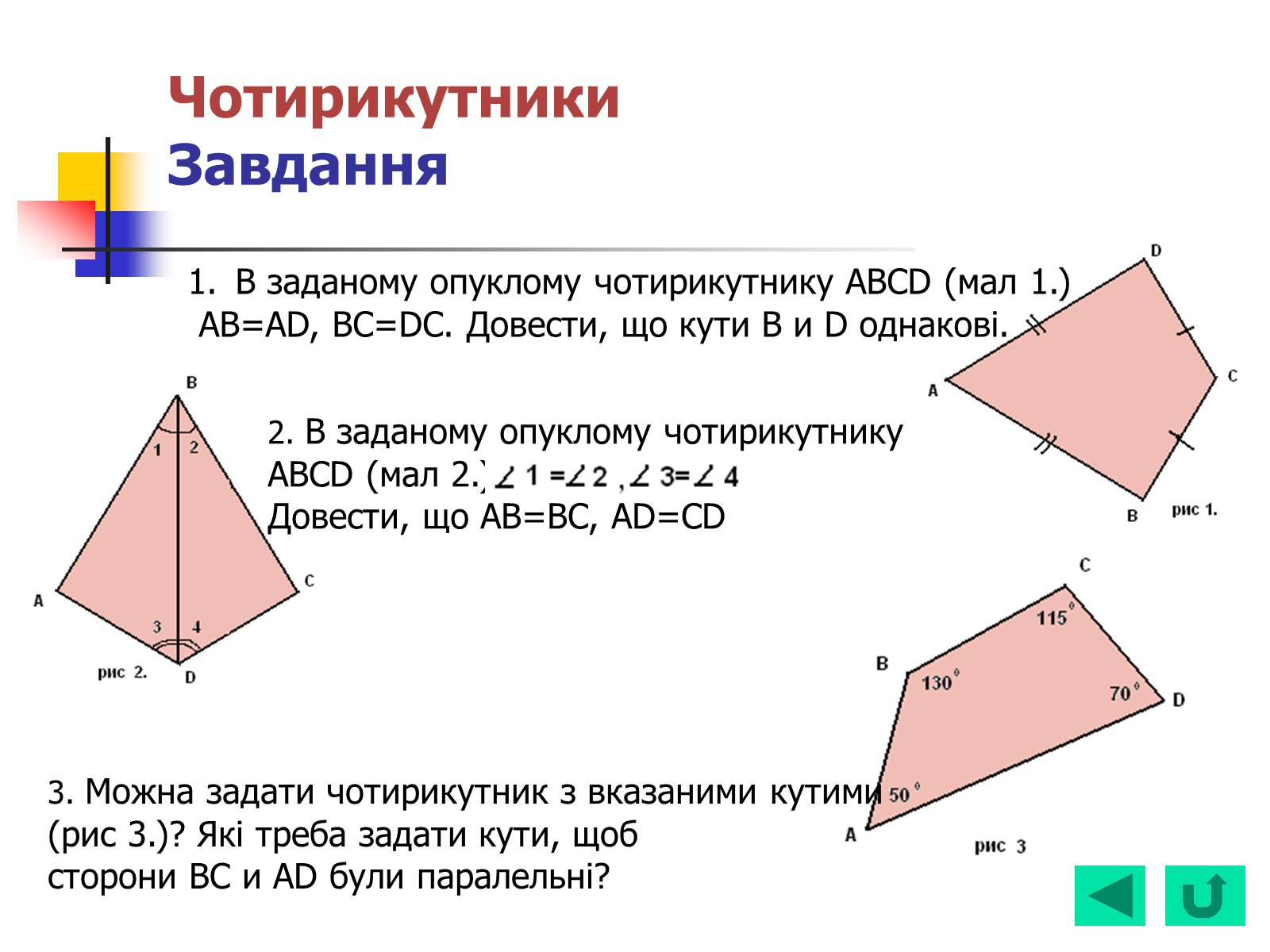
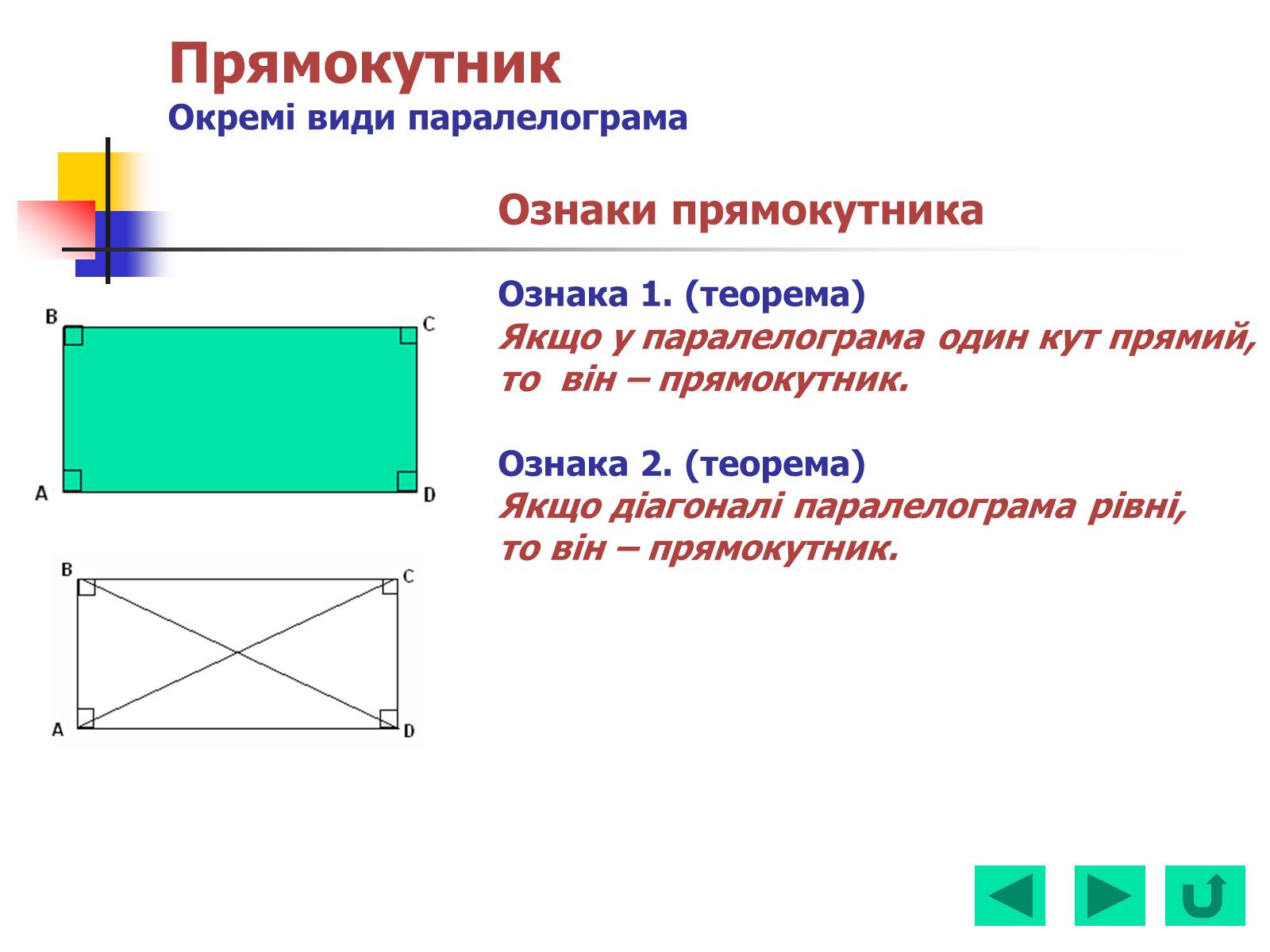
В заданому опуклому чотирикутнику ABCD (мал 1.)
AB=AD, BC=DC. Довести, що кути B и D однакові.
2. В заданому опуклому чотирикутнику
ABCD (мал 2.)
Довести, що AB=BC, AD=CD
3. Можна задати чотирикутник з вказаними кутими
(рис 3.)? Які треба задати кути, щоб
сторони BC и AD були паралельні?
В заданому опуклому чотирикутнику ABCD (мал 1.)
AB=AD, BC=DC. Довести, що кути B и D однакові.
2. В заданому опуклому чотирикутнику
ABCD (мал 2.)
Довести, що AB=BC, AD=CD
3. Можна задати чотирикутник з вказаними кутими
(рис 3.)? Які треба задати кути, щоб
сторони BC и AD були паралельні?
Слайд #13
Паралелограм
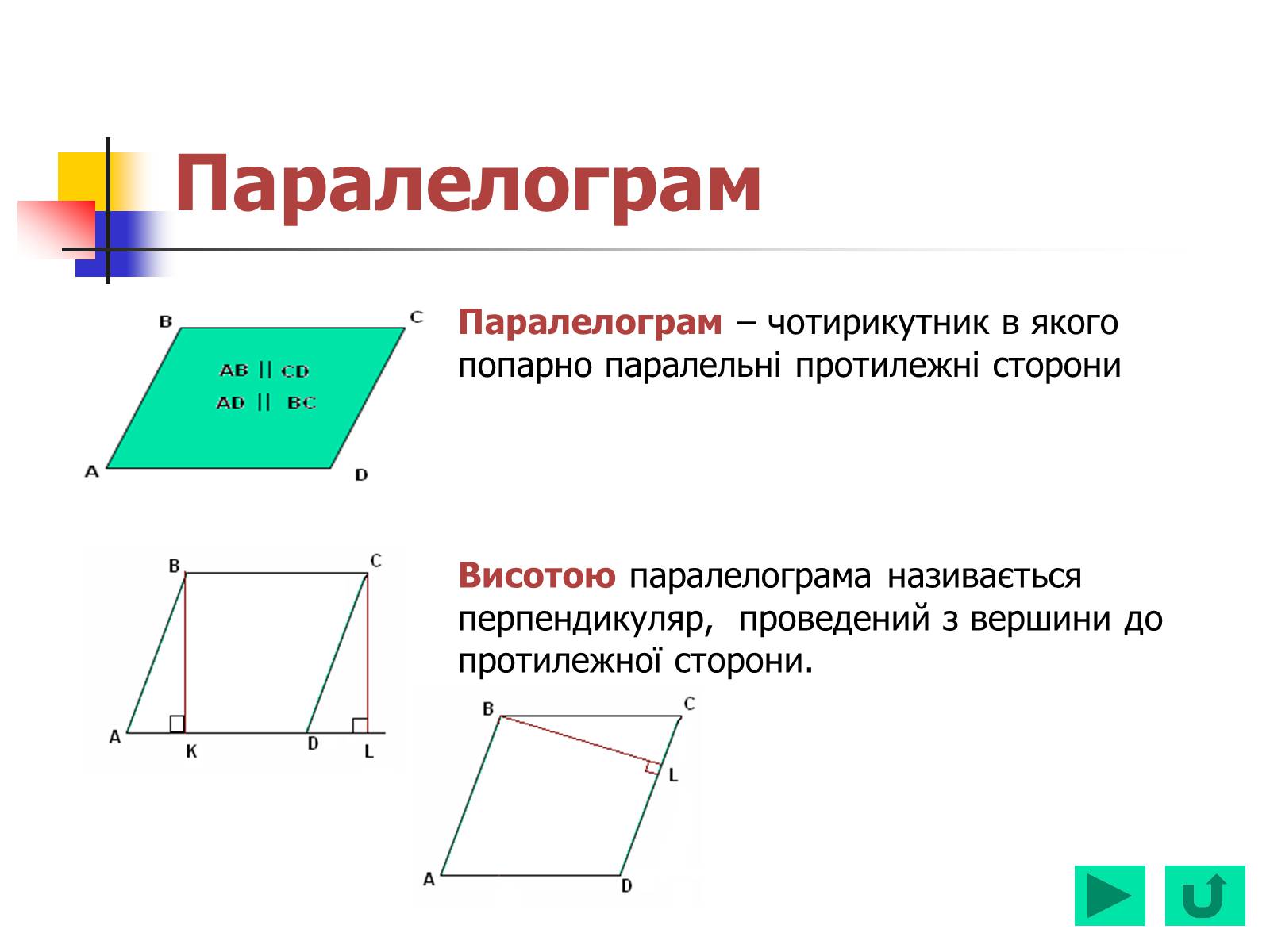
Паралелограм – чотирикутник в якого попарно паралельні протилежні сторони
Висотою паралелограма називається перпендикуляр, проведений з вершини до протилежної сторони.
Паралелограм – чотирикутник в якого попарно паралельні протилежні сторони
Висотою паралелограма називається перпендикуляр, проведений з вершини до протилежної сторони.
Слайд #14
ПаралелограмВластивості паралелограма
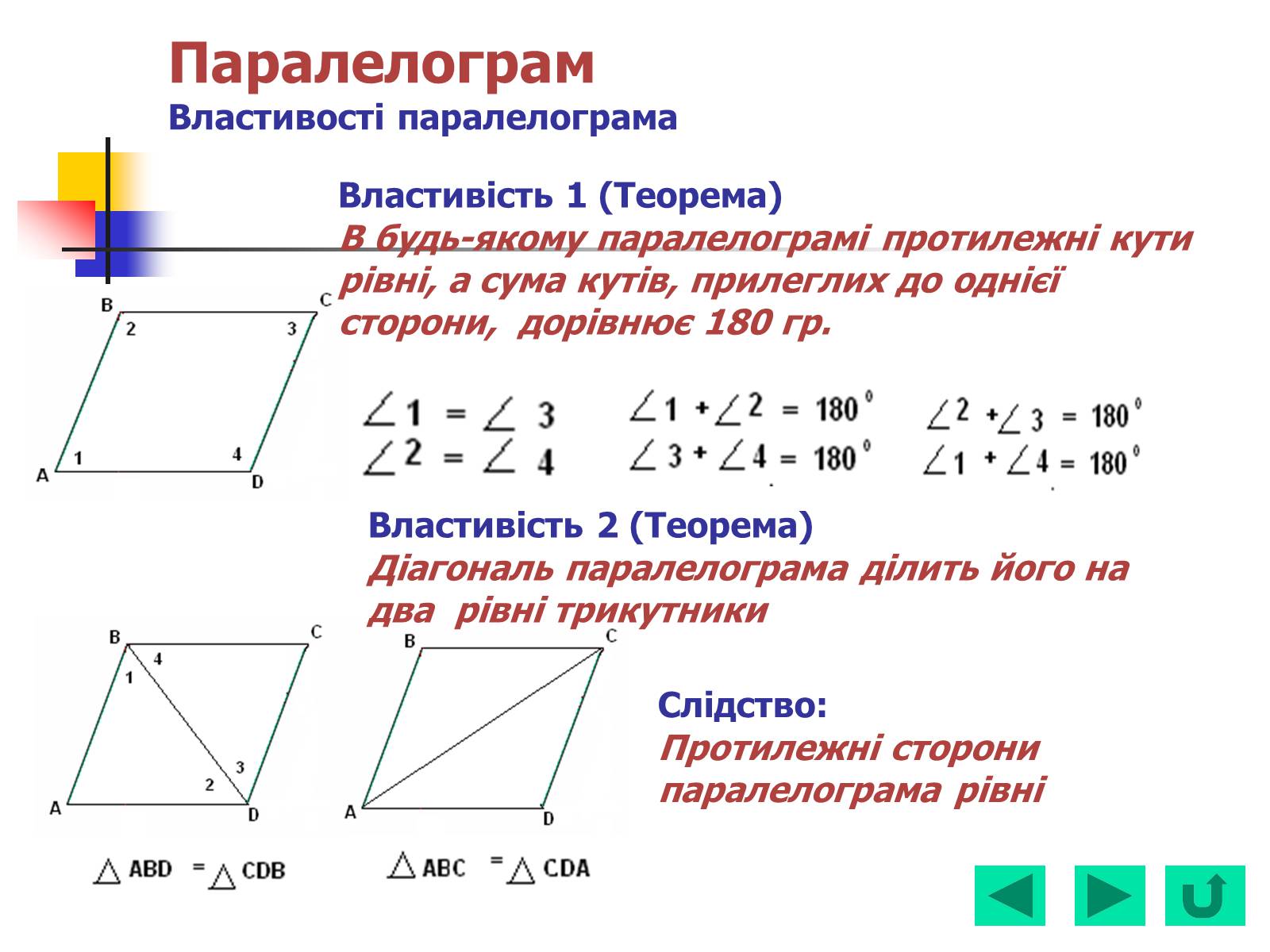
Властивість 1 (Теорема)
В будь-якому паралелограмі протилежні кути рівні, а сума кутів, прилеглих до однієї сторони, дорівнює 180 гр.
Властивість 2 (Теорема)
Діагональ паралелограма ділить його на два рівні трикутники
Слідство:
Протилежні сторони паралелограма рівні
Властивість 1 (Теорема)
В будь-якому паралелограмі протилежні кути рівні, а сума кутів, прилеглих до однієї сторони, дорівнює 180 гр.
Властивість 2 (Теорема)
Діагональ паралелограма ділить його на два рівні трикутники
Слідство:
Протилежні сторони паралелограма рівні
Слайд #15
ПаралелограмВластивості паралелограма
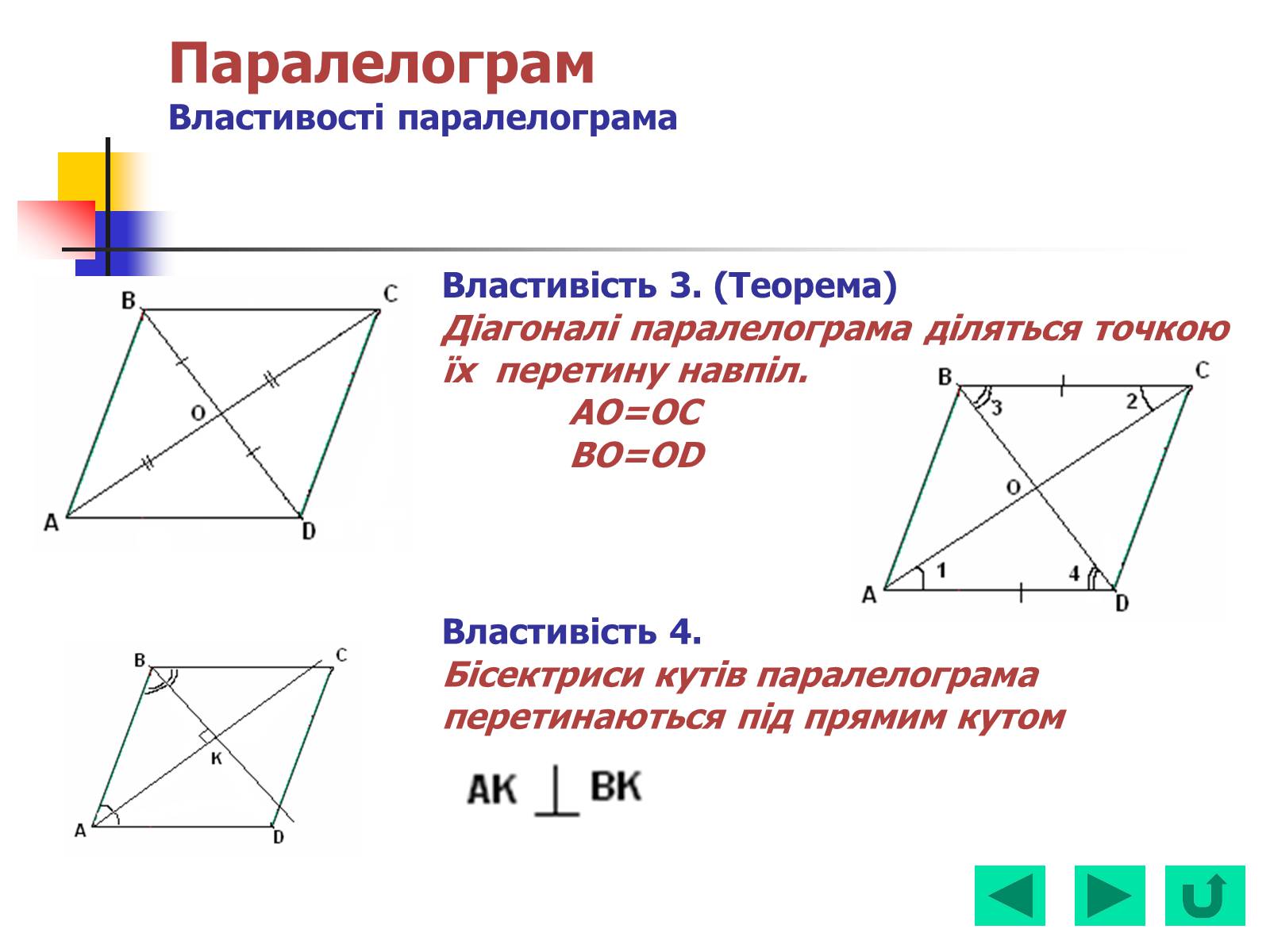
Властивість 3. (Теорема)
Діагоналі паралелограма діляться точкою їх перетину навпіл.
AO=OC
BO=OD
Властивість 4.
Бісектриси кутів паралелограма
перетинаються під прямим кутом
Властивість 3. (Теорема)
Діагоналі паралелограма діляться точкою їх перетину навпіл.
AO=OC
BO=OD
Властивість 4.
Бісектриси кутів паралелограма
перетинаються під прямим кутом
Слайд #16
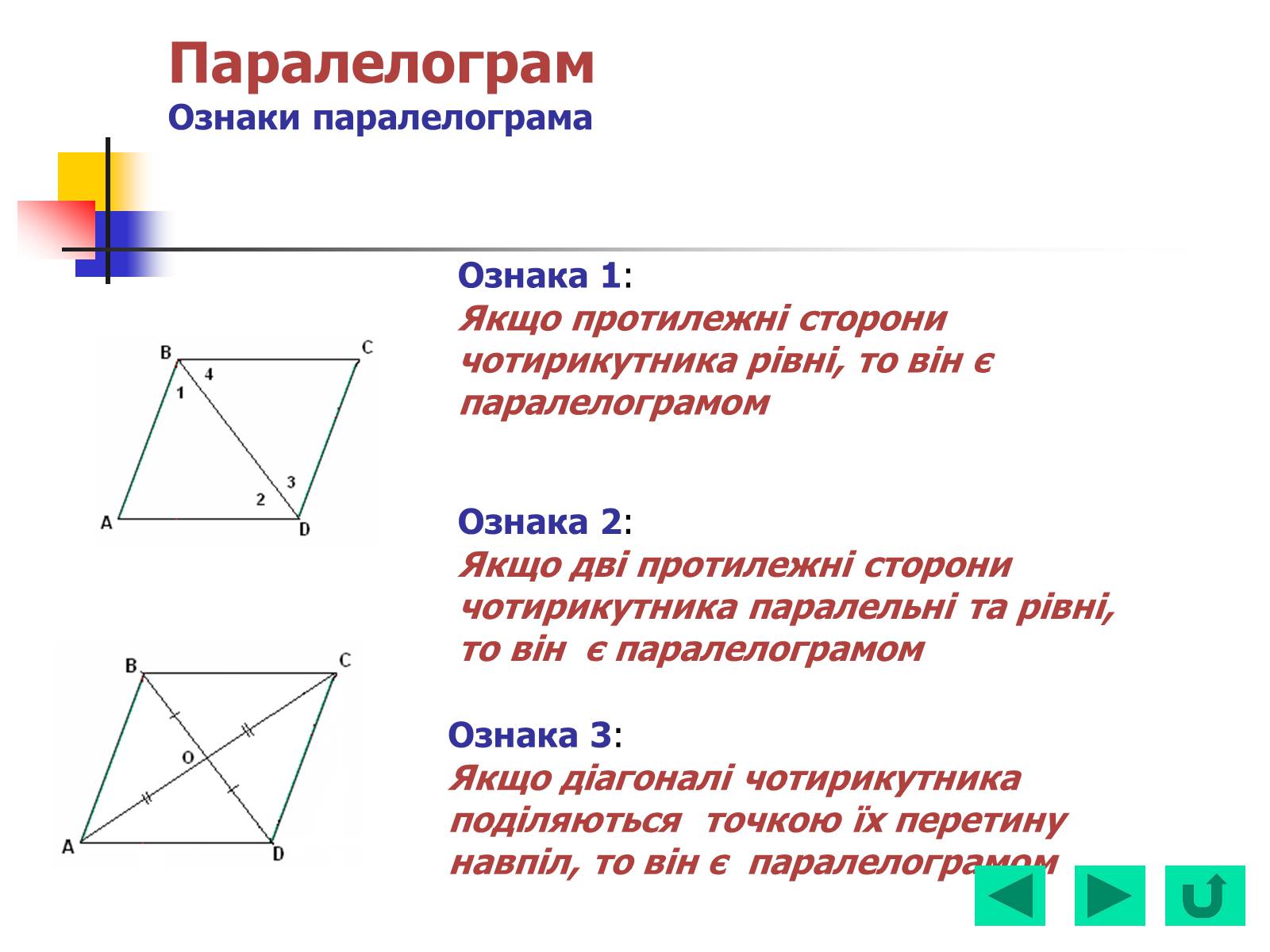
ПаралелограмОзнаки паралелограма
Ознака 1:
Якщо протилежні сторони
чотирикутника рівні, то він є
паралелограмом
Ознака 2:
Якщо дві протилежні сторони
чотирикутника паралельні та рівні,
то він є паралелограмом
Ознака 3:
Якщо діагоналі чотирикутника поділяються точкою їх перетину навпіл, то він є паралелограмом
Ознака 1:
Якщо протилежні сторони
чотирикутника рівні, то він є
паралелограмом
Ознака 2:
Якщо дві протилежні сторони
чотирикутника паралельні та рівні,
то він є паралелограмом
Ознака 3:
Якщо діагоналі чотирикутника поділяються точкою їх перетину навпіл, то він є паралелограмом
Слайд #17
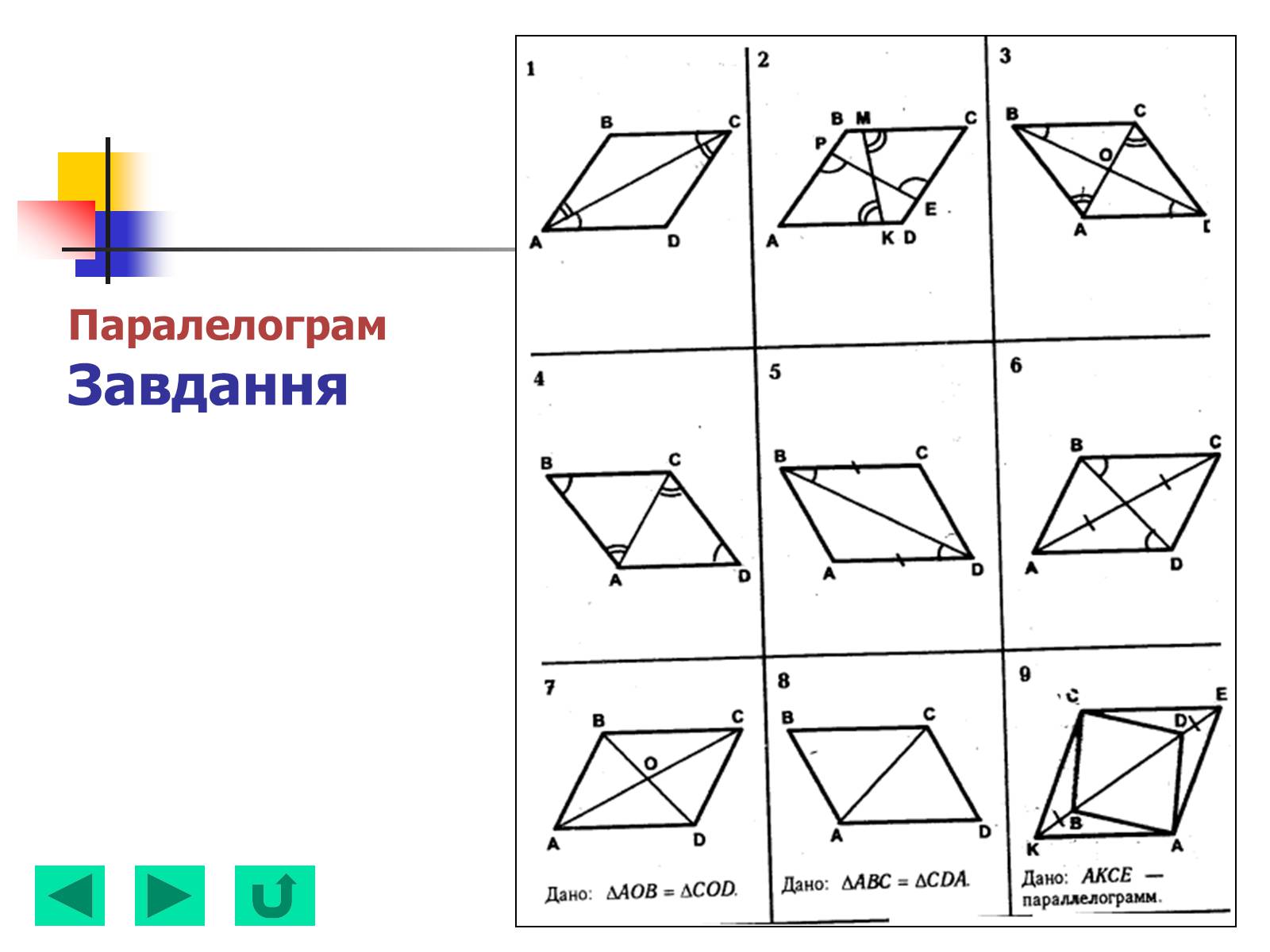
ПаралелограмЗавдання
Слайд #18
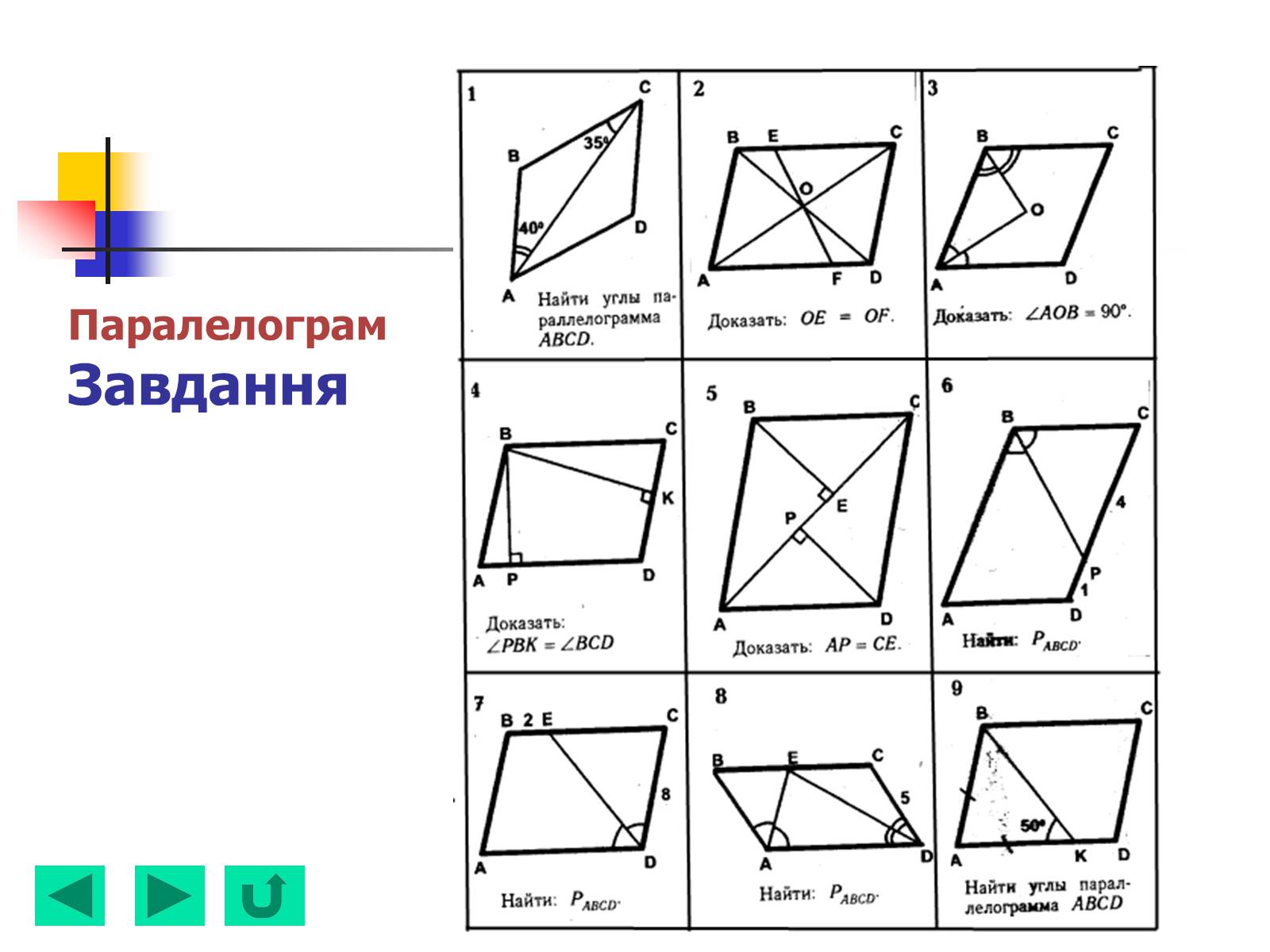
ПаралелограмЗавдання
Слайд #19
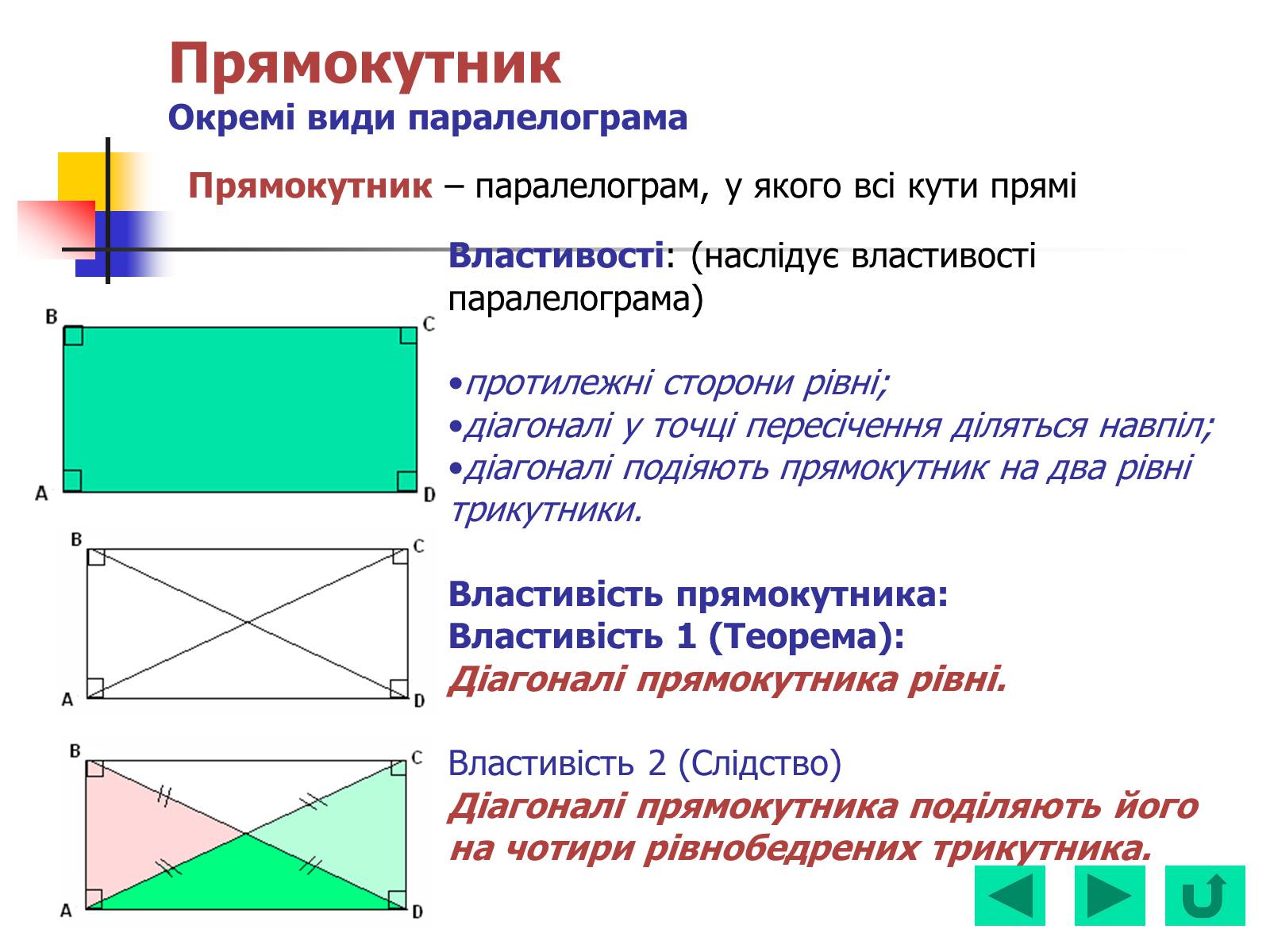
Прямокутник Окремі види паралелограма
Властивості: (наслідує властивості паралелограма)
протилежні сторони рівні;
діагоналі у точці пересічення діляться навпіл;
діагоналі подіяють прямокутник на два рівні трикутники.
Властивість прямокутника:
Властивість 1 (Теорема):
Діагоналі прямокутника рівні.
Властивість 2 (Слідство)
Діагоналі прямокутника поділяють його на чотири рівнобедрених трикутника.
Прямокутник – паралелограм, у якого всі кути прямі
Властивості: (наслідує властивості паралелограма)
протилежні сторони рівні;
діагоналі у точці пересічення діляться навпіл;
діагоналі подіяють прямокутник на два рівні трикутники.
Властивість прямокутника:
Властивість 1 (Теорема):
Діагоналі прямокутника рівні.
Властивість 2 (Слідство)
Діагоналі прямокутника поділяють його на чотири рівнобедрених трикутника.
Прямокутник – паралелограм, у якого всі кути прямі
Слайд #20
Прямокутник Окремі види паралелограма
Ознаки прямокутника
Ознака 1. (теорема)
Якщо у паралелограма один кут прямий,
то він – прямокутник.
Ознака 2. (теорема)
Якщо діагоналі паралелограма рівні,
то він – прямокутник.
Ознаки прямокутника
Ознака 1. (теорема)
Якщо у паралелограма один кут прямий,
то він – прямокутник.
Ознака 2. (теорема)
Якщо діагоналі паралелограма рівні,
то він – прямокутник.
Слайд #21
ПрямокутникЗавдання
Слайд #22
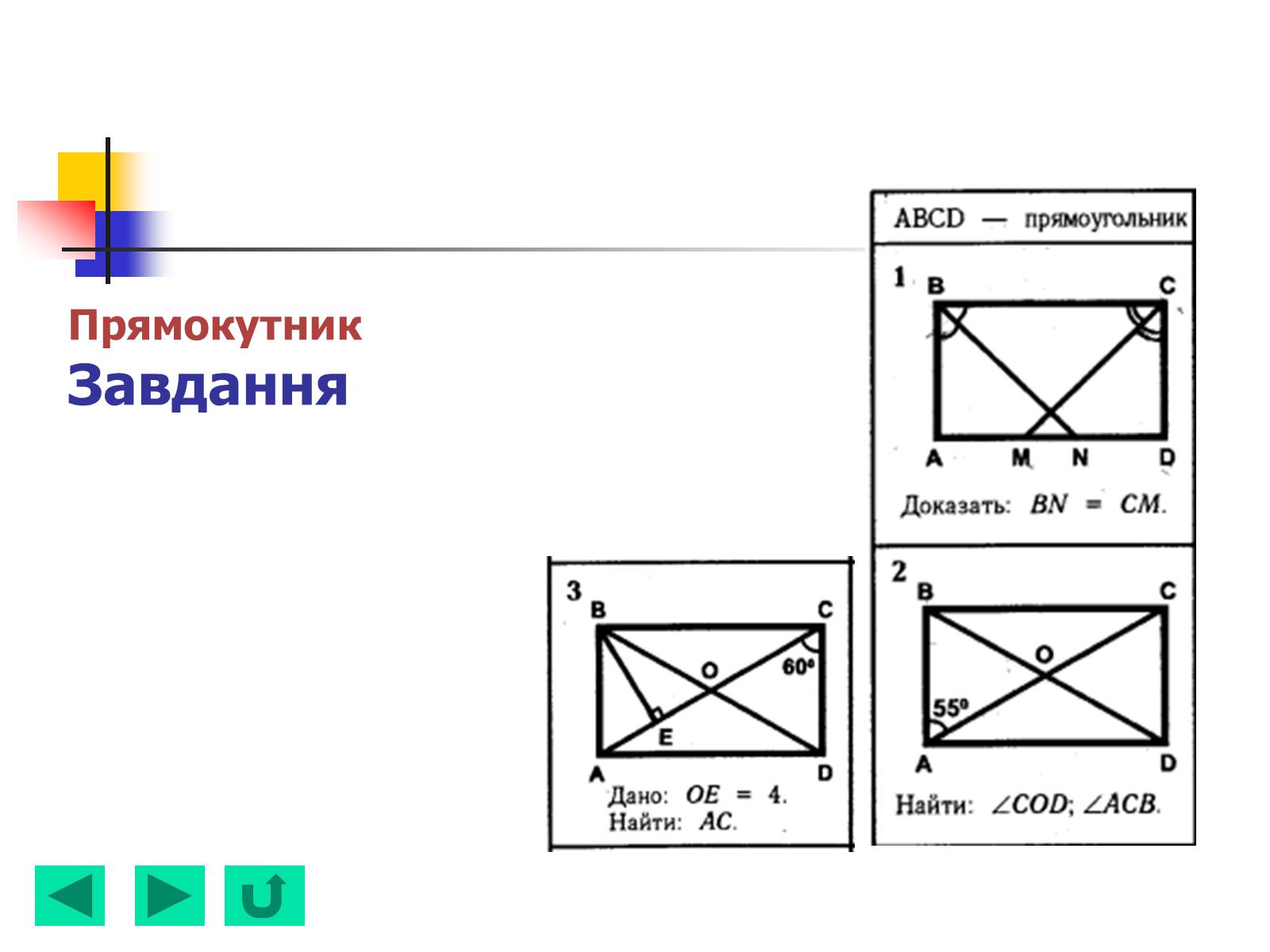
ПрямокутникВписані прямокутники
Теорема
Навколо будь якого прямокутника можна описати коло.
(серединні перпендикуляри сторін перетинатимуться в одній точці;
Сума протилежних кутів дорівнює 180 гр.)
Центром описаного кола буде точка – перетин діагоналей.
Ознаки прямокутника
Якщо навколо паралелограма можна описати коло,
то він є прямокутником.
Теорема
Навколо будь якого прямокутника можна описати коло.
(серединні перпендикуляри сторін перетинатимуться в одній точці;
Сума протилежних кутів дорівнює 180 гр.)
Центром описаного кола буде точка – перетин діагоналей.
Ознаки прямокутника
Якщо навколо паралелограма можна описати коло,
то він є прямокутником.
Слайд #23
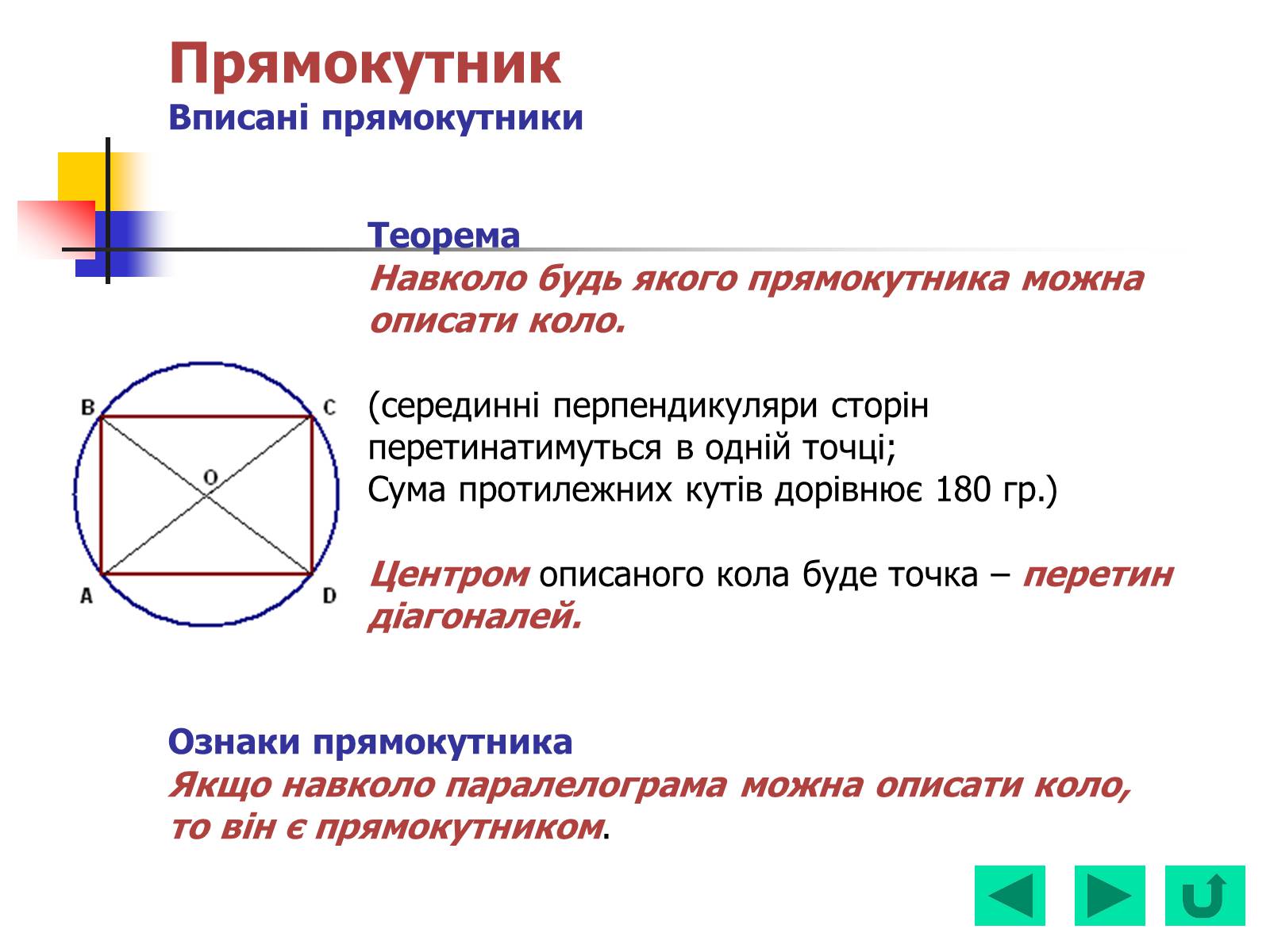
Ромб Окремі види паралелограма
Ромб – паралелограм у якого всі сторони рівні
Властивості: (наслідує властивості паралелограма)
протилежні кути рівні;
сума кутів, прилеглих до однієї сторони, дорівнює 180 гр;
діагоналі в точці перетину діляться навпіл;
Властивість ромба: В ромбі діагоналі взаємно перпендикулярні і є бісектрисами його кутів.
Якщо ABCD ромб, то
Ромб – паралелограм у якого всі сторони рівні
Властивості: (наслідує властивості паралелограма)
протилежні кути рівні;
сума кутів, прилеглих до однієї сторони, дорівнює 180 гр;
діагоналі в точці перетину діляться навпіл;
Властивість ромба: В ромбі діагоналі взаємно перпендикулярні і є бісектрисами його кутів.
Якщо ABCD ромб, то
Слайд #24
Ромб Окремі види паралелограма
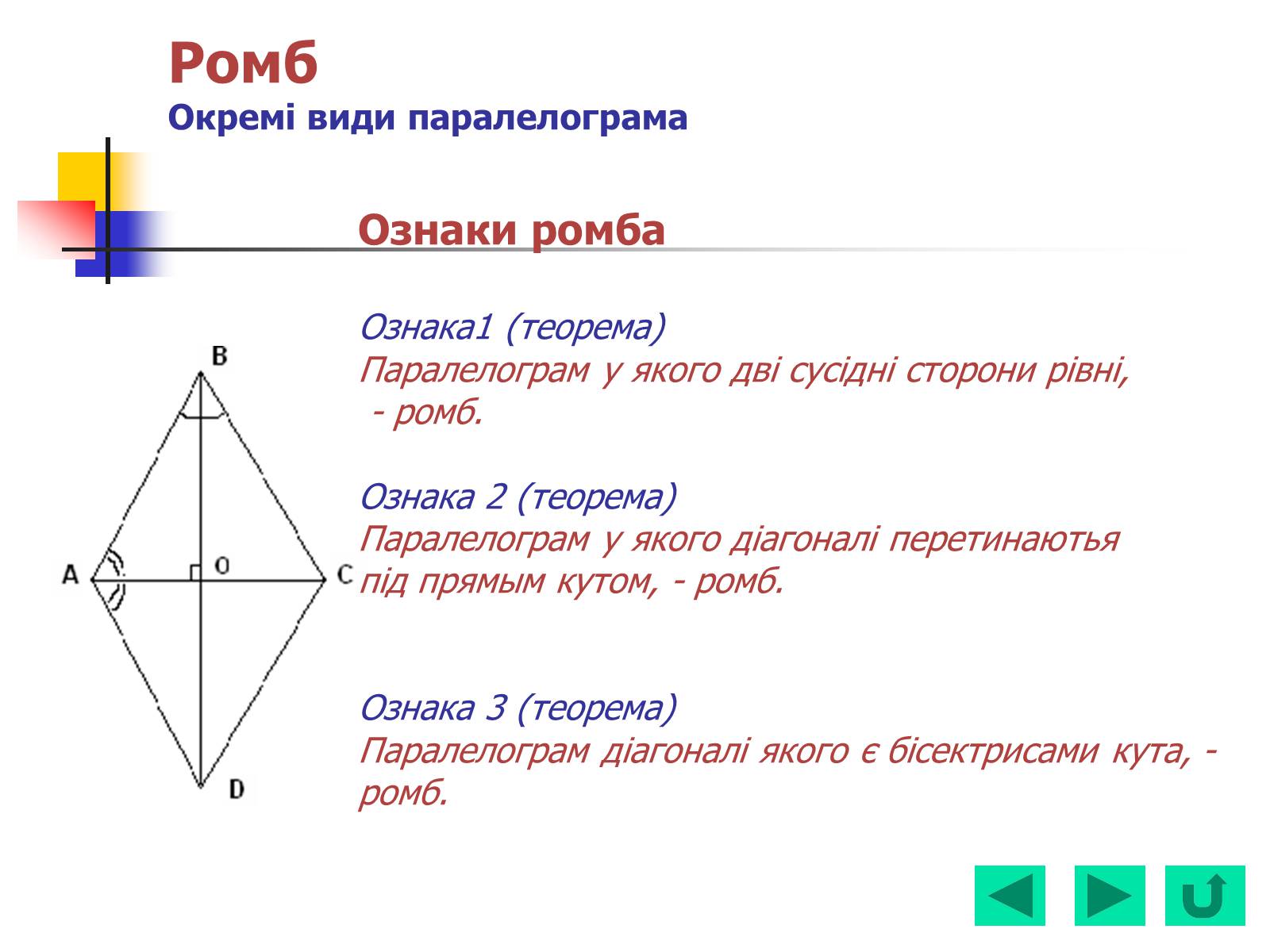
Ознаки ромба
Ознака1 (теорема)
Паралелограм у якого дві сусідні сторони рівні,
- ромб.
Ознака 2 (теорема)
Паралелограм у якого діагоналі перетинаютья
під прямым кутом, - ромб.
Ознака 3 (теорема)
Паралелограм діагоналі якого є бісектрисами кута, - ромб.
Ознаки ромба
Ознака1 (теорема)
Паралелограм у якого дві сусідні сторони рівні,
- ромб.
Ознака 2 (теорема)
Паралелограм у якого діагоналі перетинаютья
під прямым кутом, - ромб.
Ознака 3 (теорема)
Паралелограм діагоналі якого є бісектрисами кута, - ромб.
Слайд #25
Ромб Описані ромби
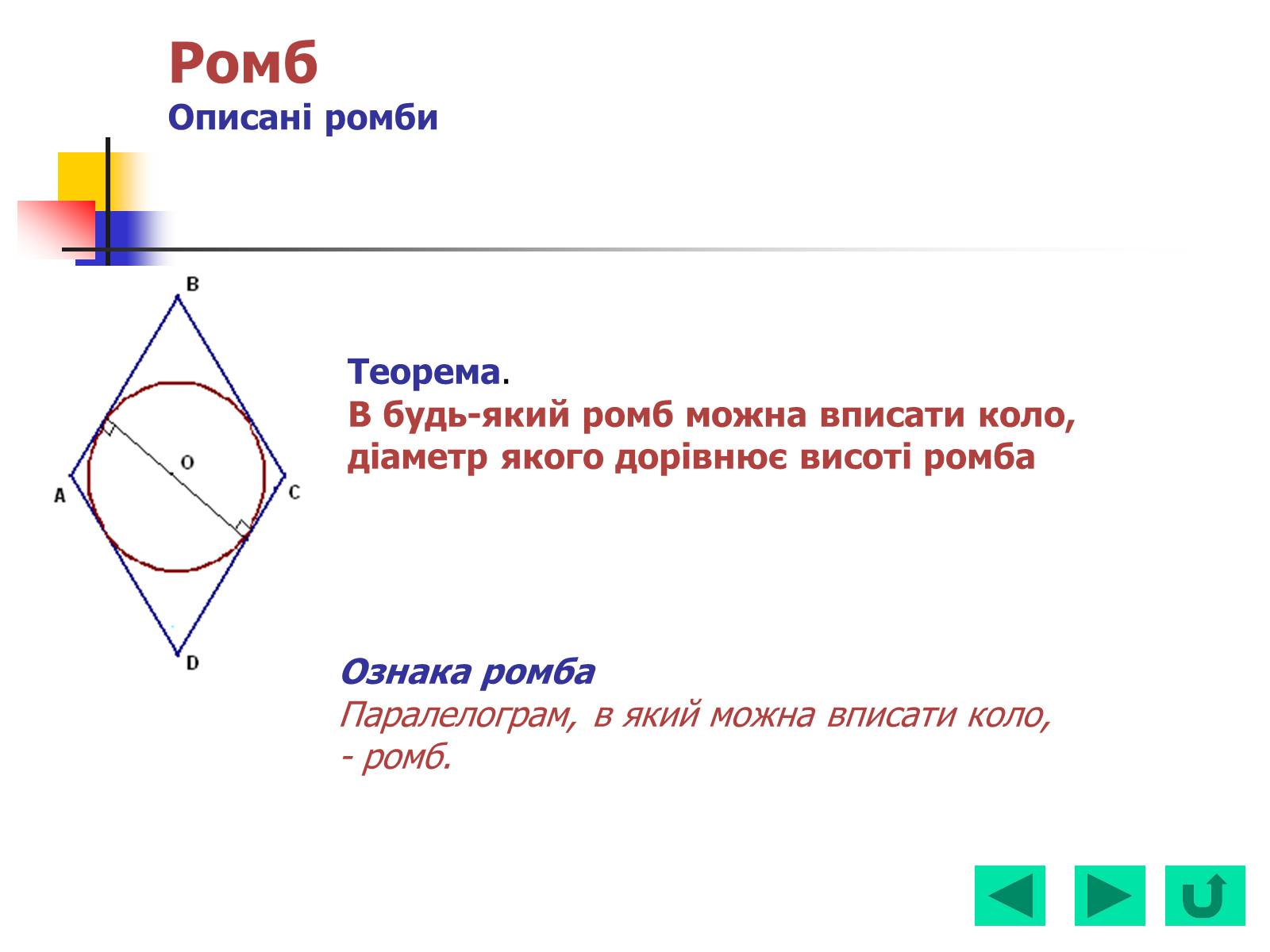
Теорема.
В будь-який ромб можна вписати коло, діаметр якого дорівнює висоті ромба
Ознака ромба
Паралелограм, в який можна вписати коло,
- ромб.
Теорема.
В будь-який ромб можна вписати коло, діаметр якого дорівнює висоті ромба
Ознака ромба
Паралелограм, в який можна вписати коло,
- ромб.
Слайд #26
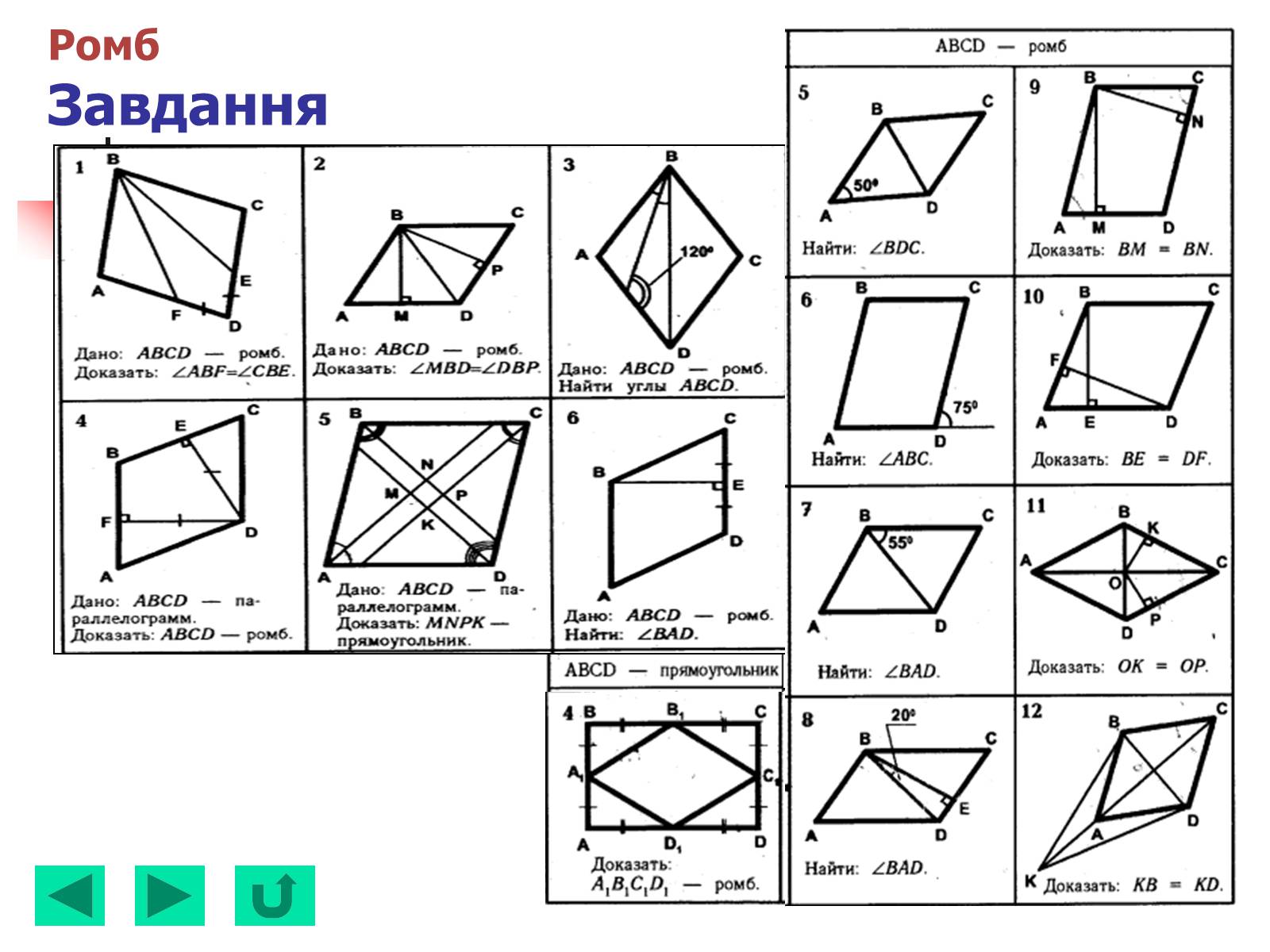
РомбЗавдання
Слайд #27
Квадрат Окремі види паралелограма
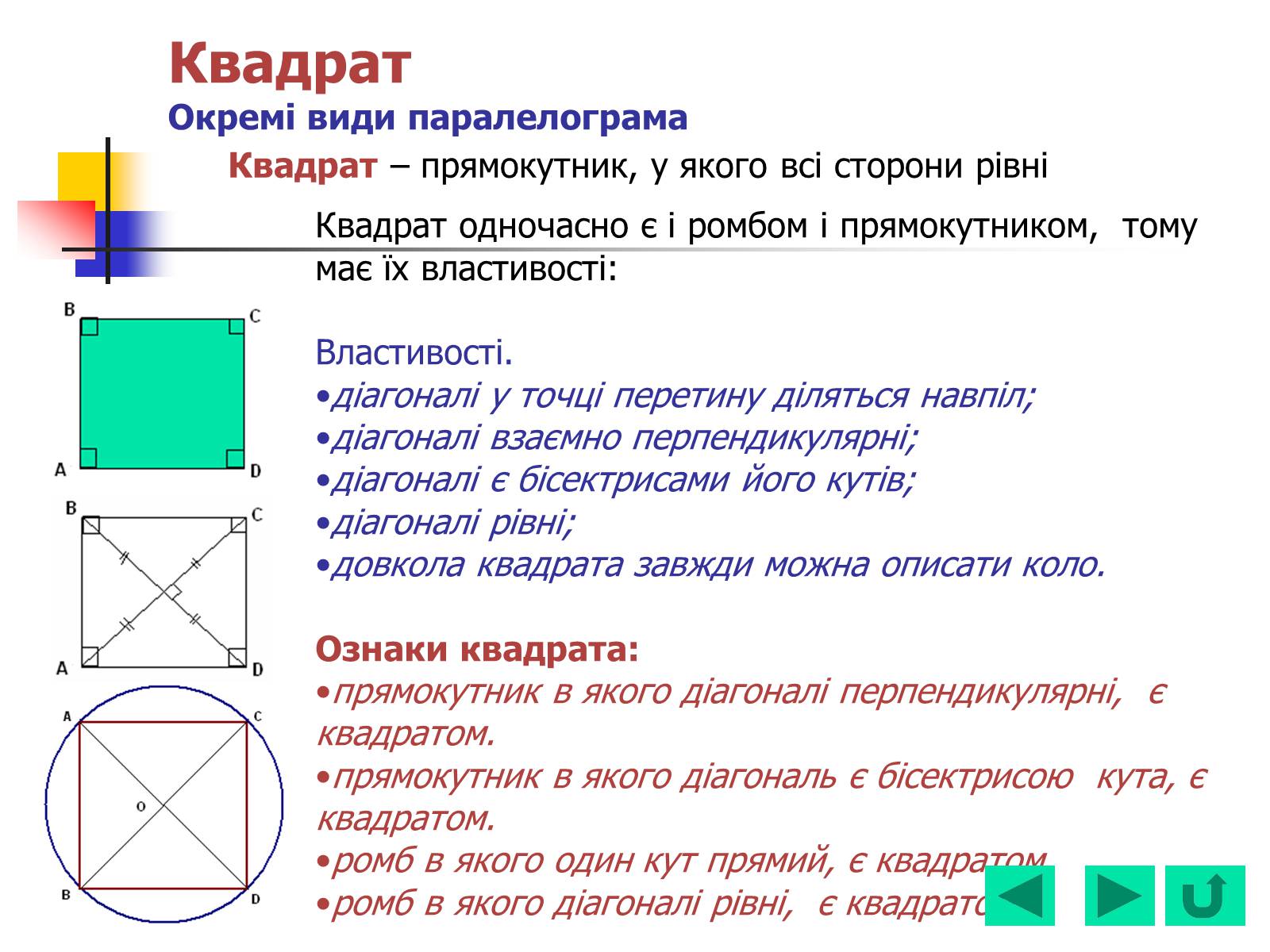
Квадрат – прямокутник, у якого всі сторони рівні
Квадрат одночасно є і ромбом і прямокутником, тому має їх властивості:
Властивості.
діагоналі у точці перетину діляться навпіл;
діагоналі взаємно перпендикулярні;
діагоналі є бісектрисами його кутів;
діагоналі рівні;
довкола квадрата завжди можна описати коло.
Ознаки квадрата:
прямокутник в якого діагоналі перпендикулярні, є квадратом.
прямокутник в якого діагональ є бісектрисою кута, є квадратом.
ромб в якого один кут прямий, є квадратом.
ромб в якого діагоналі рівні, є квадратом.
Квадрат – прямокутник, у якого всі сторони рівні
Квадрат одночасно є і ромбом і прямокутником, тому має їх властивості:
Властивості.
діагоналі у точці перетину діляться навпіл;
діагоналі взаємно перпендикулярні;
діагоналі є бісектрисами його кутів;
діагоналі рівні;
довкола квадрата завжди можна описати коло.
Ознаки квадрата:
прямокутник в якого діагоналі перпендикулярні, є квадратом.
прямокутник в якого діагональ є бісектрисою кута, є квадратом.
ромб в якого один кут прямий, є квадратом.
ромб в якого діагоналі рівні, є квадратом.
Слайд #28
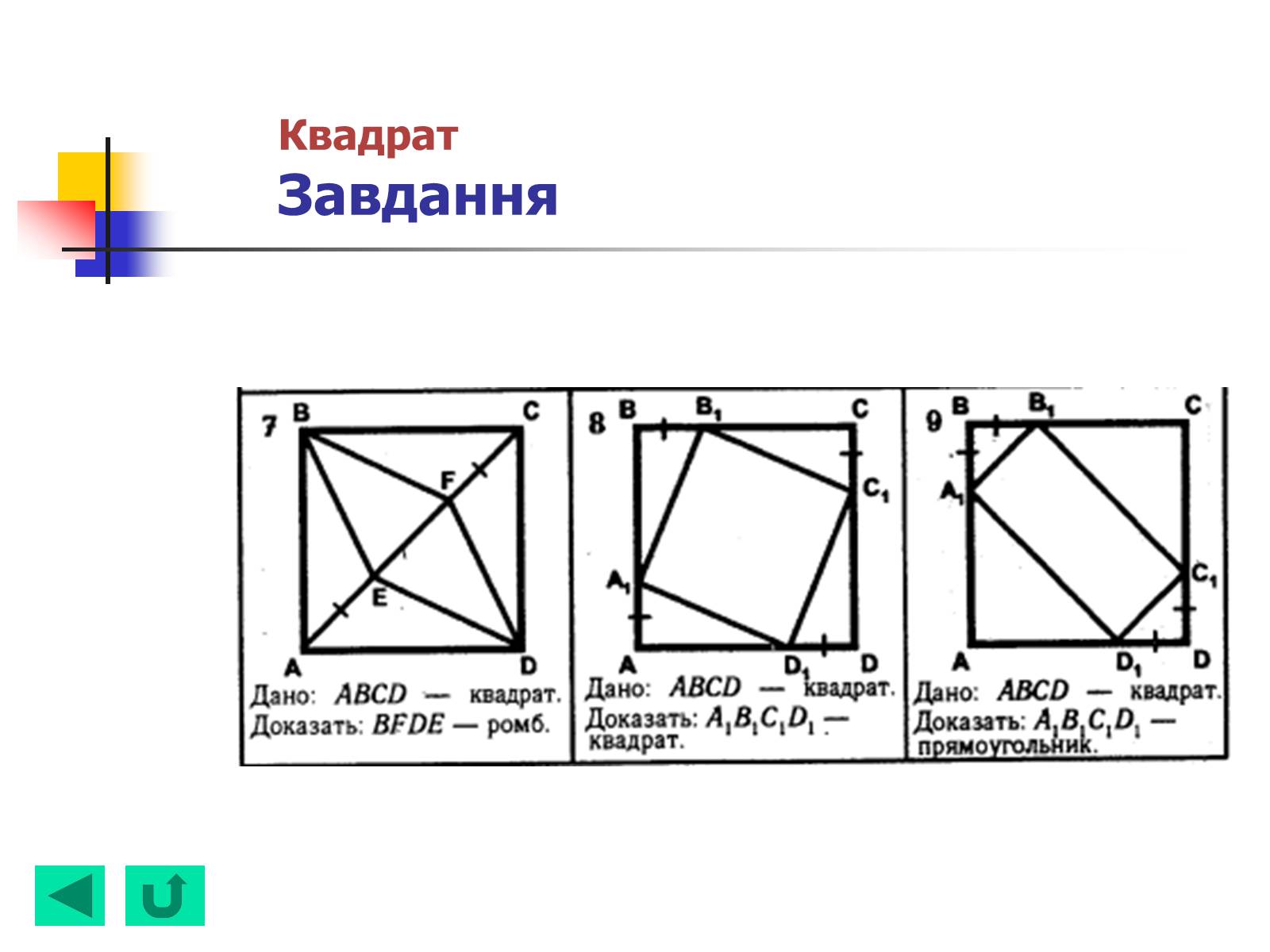
КвадратЗавдання
Слайд #29
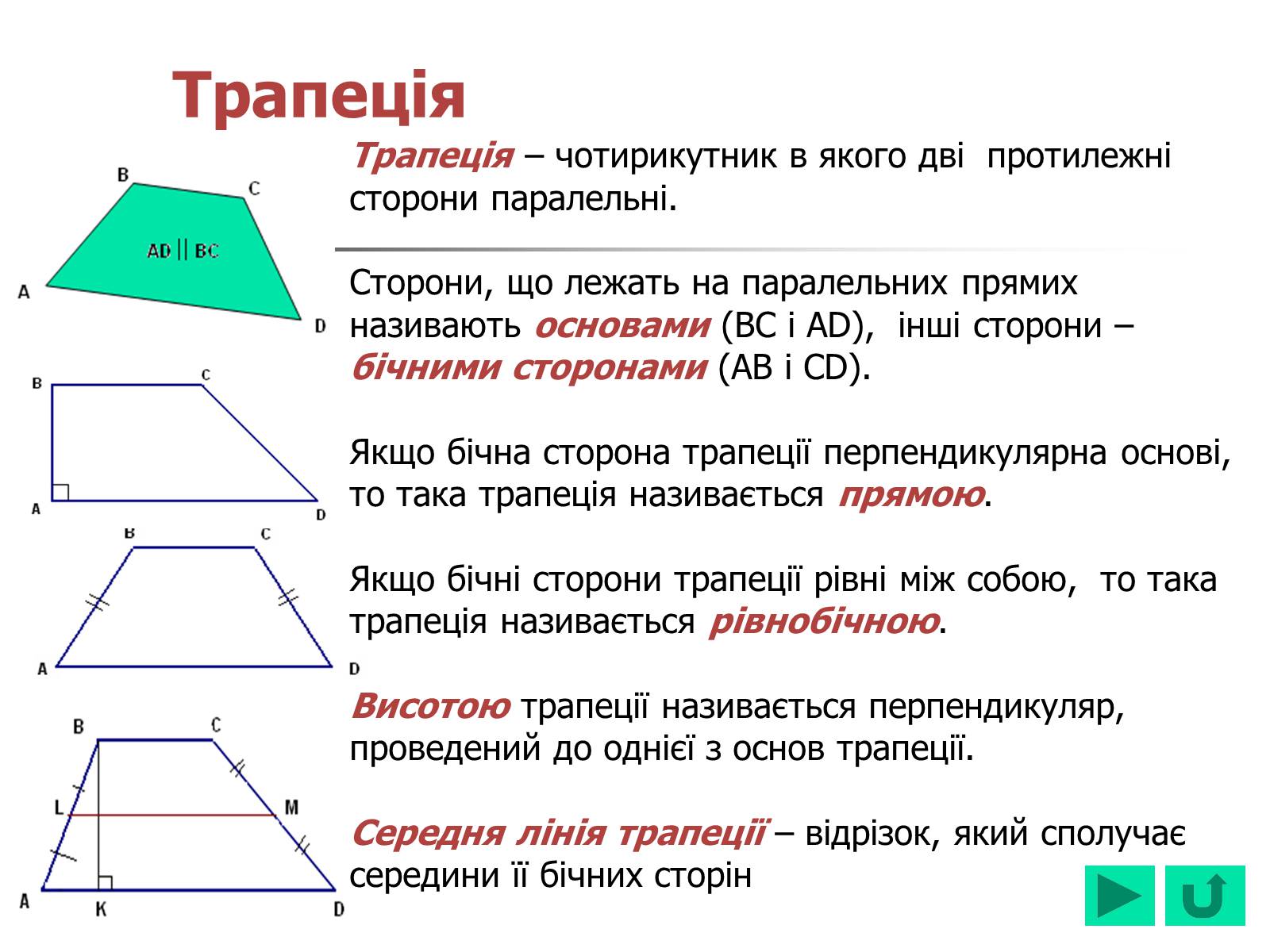
Трапеція
Трапеція – чотирикутник в якого дві протилежні сторони паралельні.
Сторони, що лежать на паралельних прямих називають основами (BC і AD), інші сторони – бічними сторонами (AB і CD).
Якщо бічна сторона трапеції перпендикулярна основі, то така трапеція називається прямою.
Якщо бічні сторони трапеції рівні між собою, то така трапеція називається рівнобічною.
Висотою трапеції називається перпендикуляр, проведений до однієї з основ трапеції.
Середня лінія трапеції – відрізок, який сполучає середини її бічних сторін
Трапеція – чотирикутник в якого дві протилежні сторони паралельні.
Сторони, що лежать на паралельних прямих називають основами (BC і AD), інші сторони – бічними сторонами (AB і CD).
Якщо бічна сторона трапеції перпендикулярна основі, то така трапеція називається прямою.
Якщо бічні сторони трапеції рівні між собою, то така трапеція називається рівнобічною.
Висотою трапеції називається перпендикуляр, проведений до однієї з основ трапеції.
Середня лінія трапеції – відрізок, який сполучає середини її бічних сторін
Слайд #30
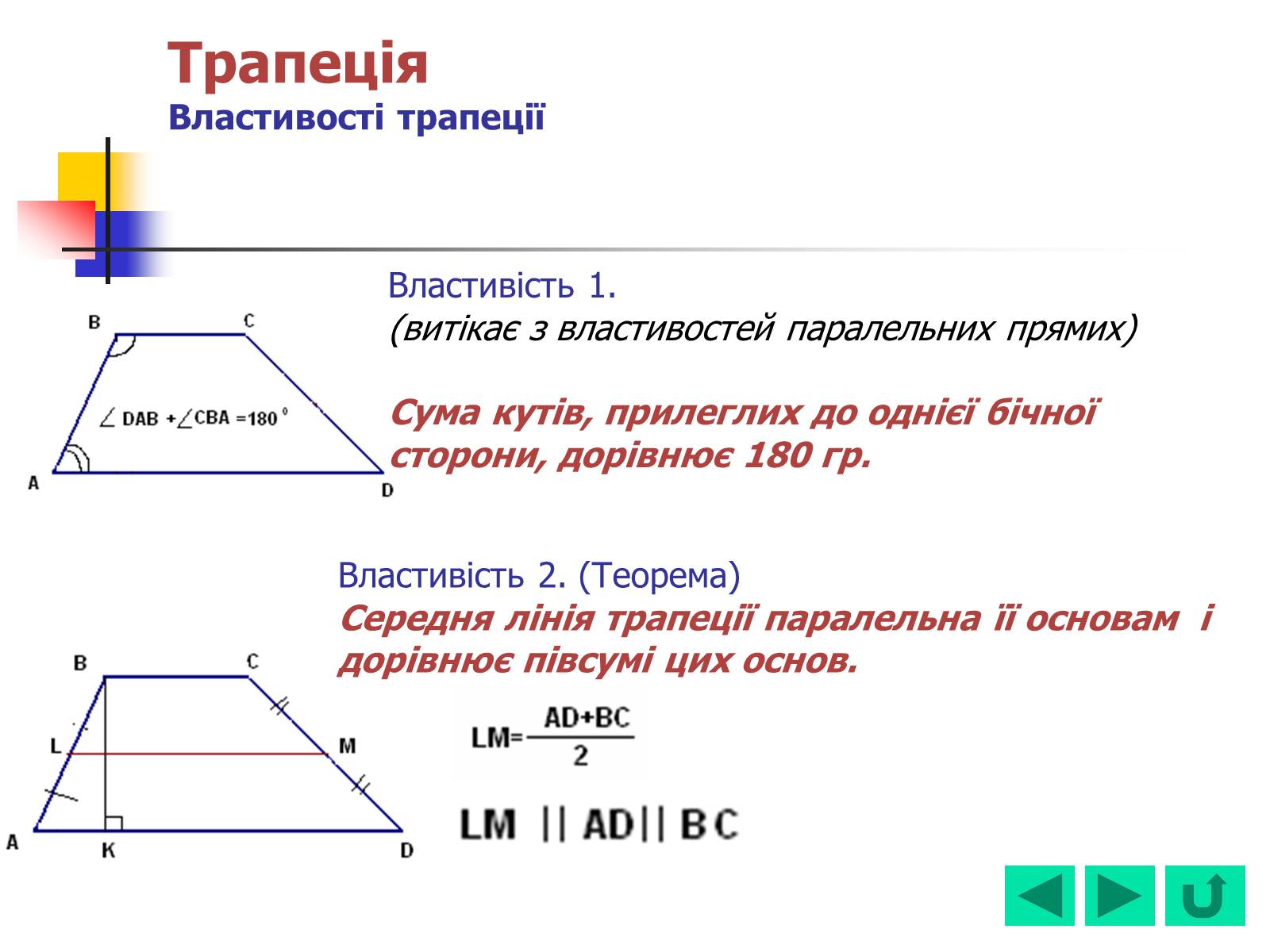
Трапеція Властивості трапеції
Властивість 1.
(витікає з властивостей паралельних прямих)
Сума кутів, прилеглих до однієї бічної сторони, дорівнює 180 гр.
Властивість 2. (Теорема)
Середня лінія трапеції паралельна її основам і дорівнює півсумі цих основ.
Властивість 1.
(витікає з властивостей паралельних прямих)
Сума кутів, прилеглих до однієї бічної сторони, дорівнює 180 гр.
Властивість 2. (Теорема)
Середня лінія трапеції паралельна її основам і дорівнює півсумі цих основ.
Слайд #31
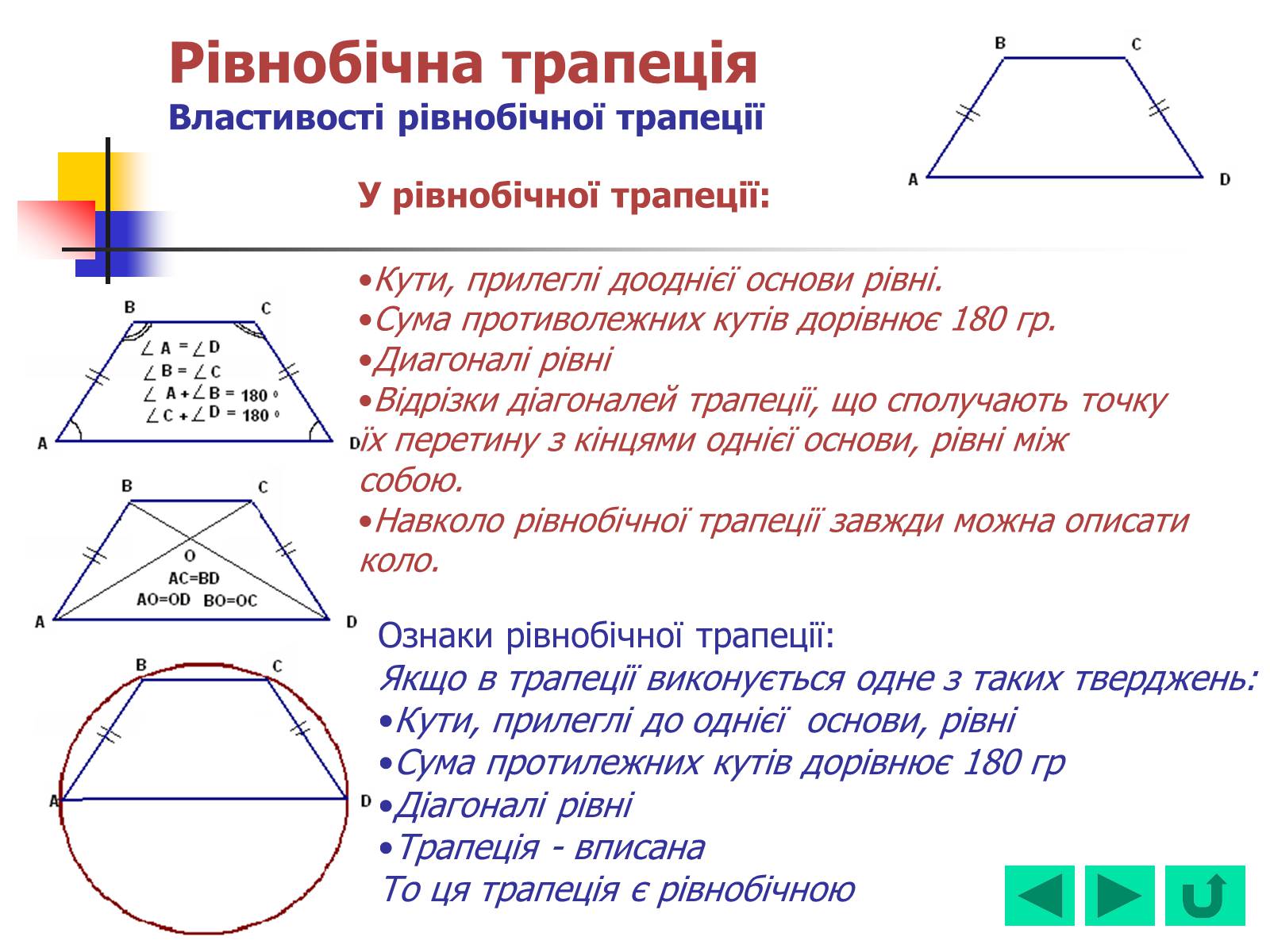
Рівнобічна трапеція Властивості рівнобічної трапеції
У рівнобічної трапеції:
Кути, прилеглі дооднієї основи рівні.
Сума противолежних кутів дорівнює 180 гр.
Диагоналі рівні
Відрізки діагоналей трапеції, що сполучають точку
їх перетину з кінцями однієї основи, рівні між
собою.
Навколо рівнобічної трапеції завжди можна описати
коло.
Ознаки рівнобічної трапеції:
Якщо в трапеції виконується одне з таких тверджень:
Кути, прилеглі до однієї основи, рівні
Сума протилежних кутів дорівнює 180 гр
Діагоналі рівні
Трапеція - вписана
То ця трапеція є рівнобічною
У рівнобічної трапеції:
Кути, прилеглі дооднієї основи рівні.
Сума противолежних кутів дорівнює 180 гр.
Диагоналі рівні
Відрізки діагоналей трапеції, що сполучають точку
їх перетину з кінцями однієї основи, рівні між
собою.
Навколо рівнобічної трапеції завжди можна описати
коло.
Ознаки рівнобічної трапеції:
Якщо в трапеції виконується одне з таких тверджень:
Кути, прилеглі до однієї основи, рівні
Сума протилежних кутів дорівнює 180 гр
Діагоналі рівні
Трапеція - вписана
То ця трапеція є рівнобічною
Слайд #32
Трапеція Завдання
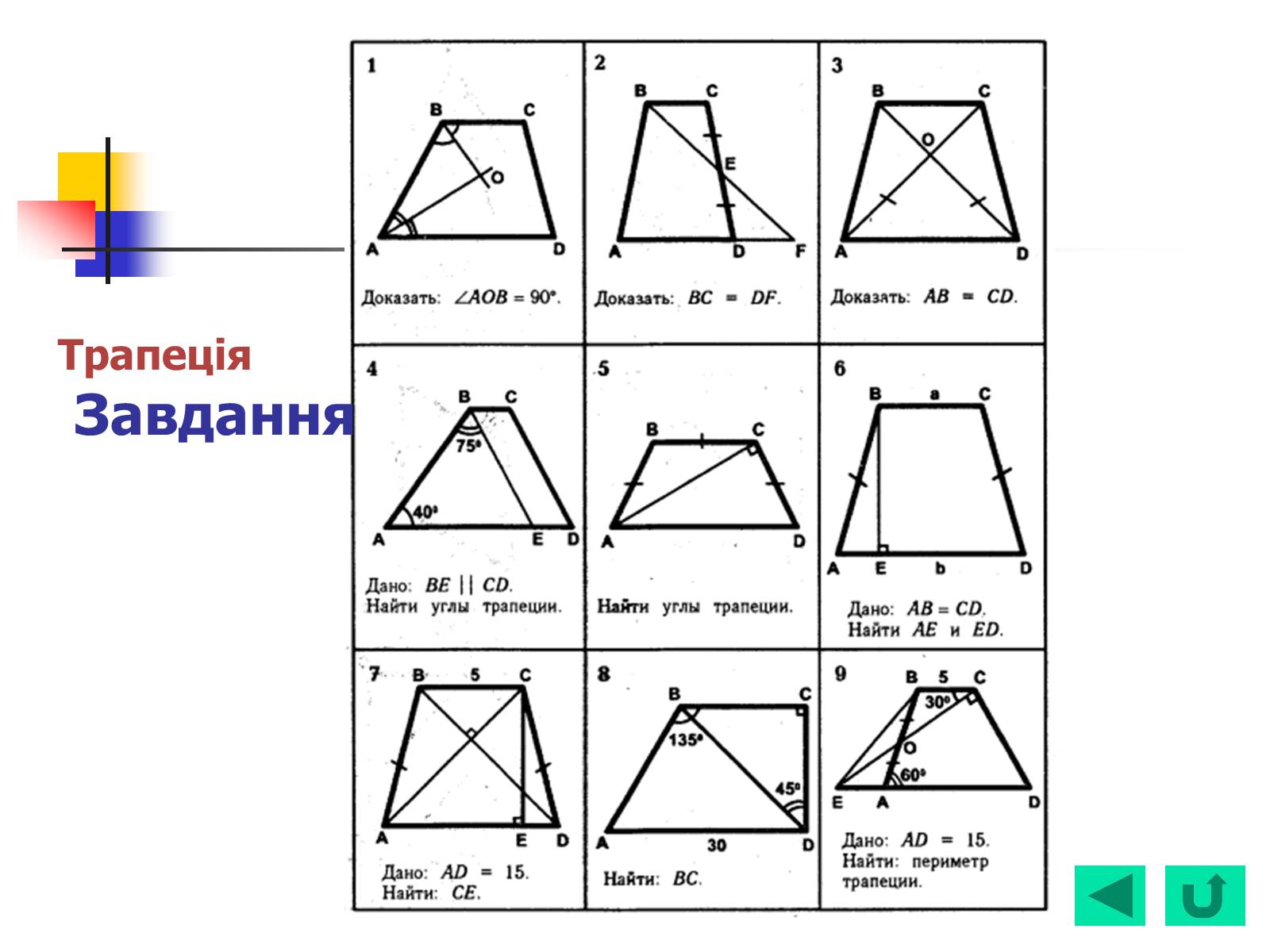
Слайд #33
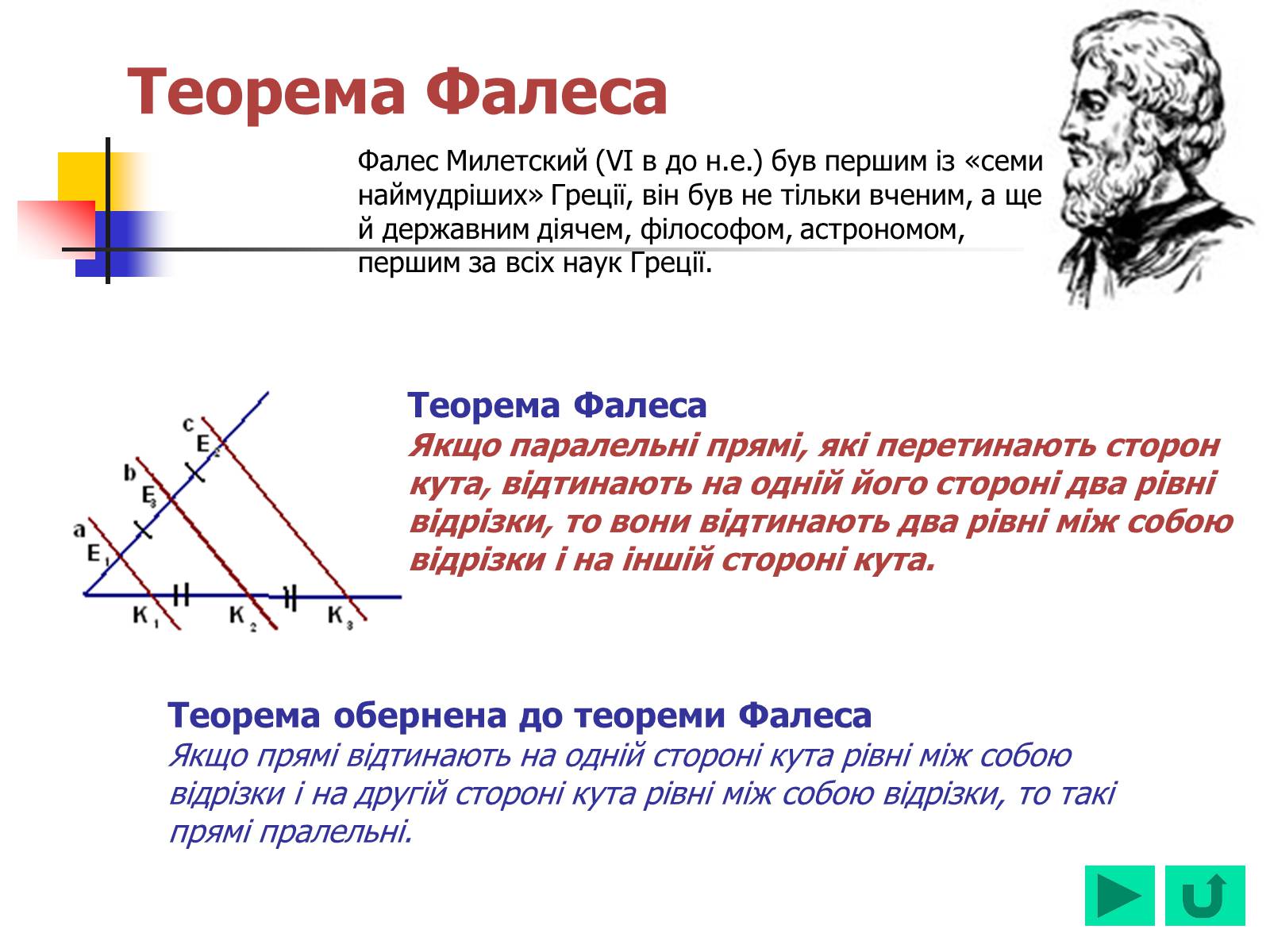
Теорема Фалеса
Теорема Фалеса
Якщо паралельні прямі, які перетинають сторон кута, відтинають на одній його стороні два рівні відрізки, то вони відтинають два рівні між собою відрізки і на іншій стороні кута.
Теорема обернена до теореми Фалеса
Якщо прямі відтинають на одній стороні кута рівні між собою відрізки і на другій стороні кута рівні між собою відрізки, то такі прямі пралельні.
Фалес Милетский (VI в до н.е.) був першим із «семи наймудріших» Греції, він був не тільки вченим, а ще й державним діячем, філософом, астрономом, першим за всіх наук Греції.
Теорема Фалеса
Якщо паралельні прямі, які перетинають сторон кута, відтинають на одній його стороні два рівні відрізки, то вони відтинають два рівні між собою відрізки і на іншій стороні кута.
Теорема обернена до теореми Фалеса
Якщо прямі відтинають на одній стороні кута рівні між собою відрізки і на другій стороні кута рівні між собою відрізки, то такі прямі пралельні.
Фалес Милетский (VI в до н.е.) був першим із «семи наймудріших» Греції, він був не тільки вченим, а ще й державним діячем, філософом, астрономом, першим за всіх наук Греції.
Слайд #34
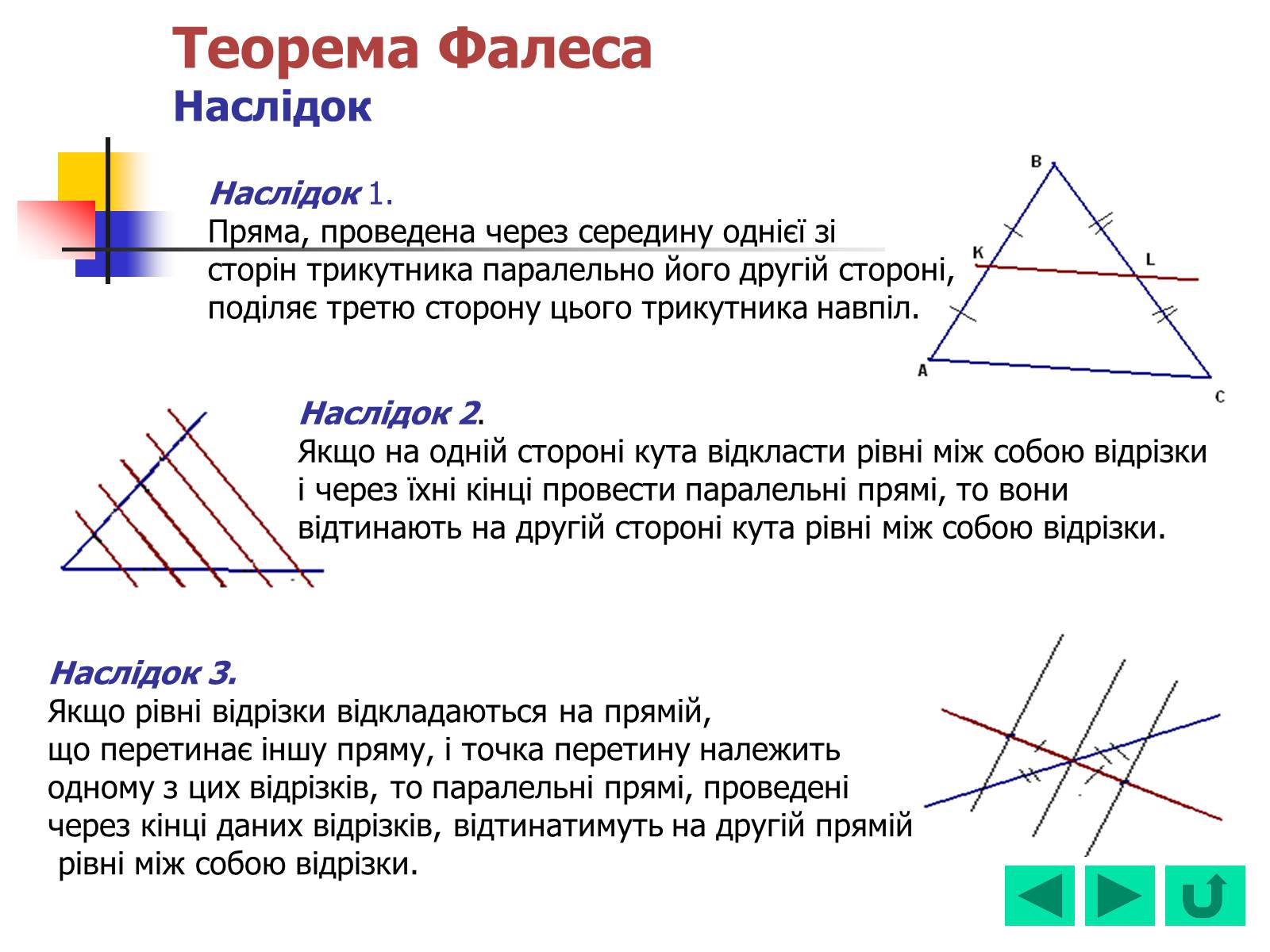
Наслідок 1.
Пряма, проведена через середину однієї зі
сторін трикутника паралельно його другій стороні,
поділяє третю сторону цього трикутника навпіл.
Наслідок 2.
Якщо на одній стороні кута відкласти рівні між собою відрізки і через їхні кінці провести паралельні прямі, то вони відтинають на другій стороні кута рівні між собою відрізки.
Наслідок 3.
Якщо рівні відрізки відкладаються на прямій,
що перетинає іншу пряму, і точка перетину належить
одному з цих відрізків, то паралельні прямі, проведені
через кінці даних відрізків, відтинатимуть на другій прямій
рівні між собою відрізки.
Теорема ФалесаНаслідок
Пряма, проведена через середину однієї зі
сторін трикутника паралельно його другій стороні,
поділяє третю сторону цього трикутника навпіл.
Наслідок 2.
Якщо на одній стороні кута відкласти рівні між собою відрізки і через їхні кінці провести паралельні прямі, то вони відтинають на другій стороні кута рівні між собою відрізки.
Наслідок 3.
Якщо рівні відрізки відкладаються на прямій,
що перетинає іншу пряму, і точка перетину належить
одному з цих відрізків, то паралельні прямі, проведені
через кінці даних відрізків, відтинатимуть на другій прямій
рівні між собою відрізки.
Теорема ФалесаНаслідок
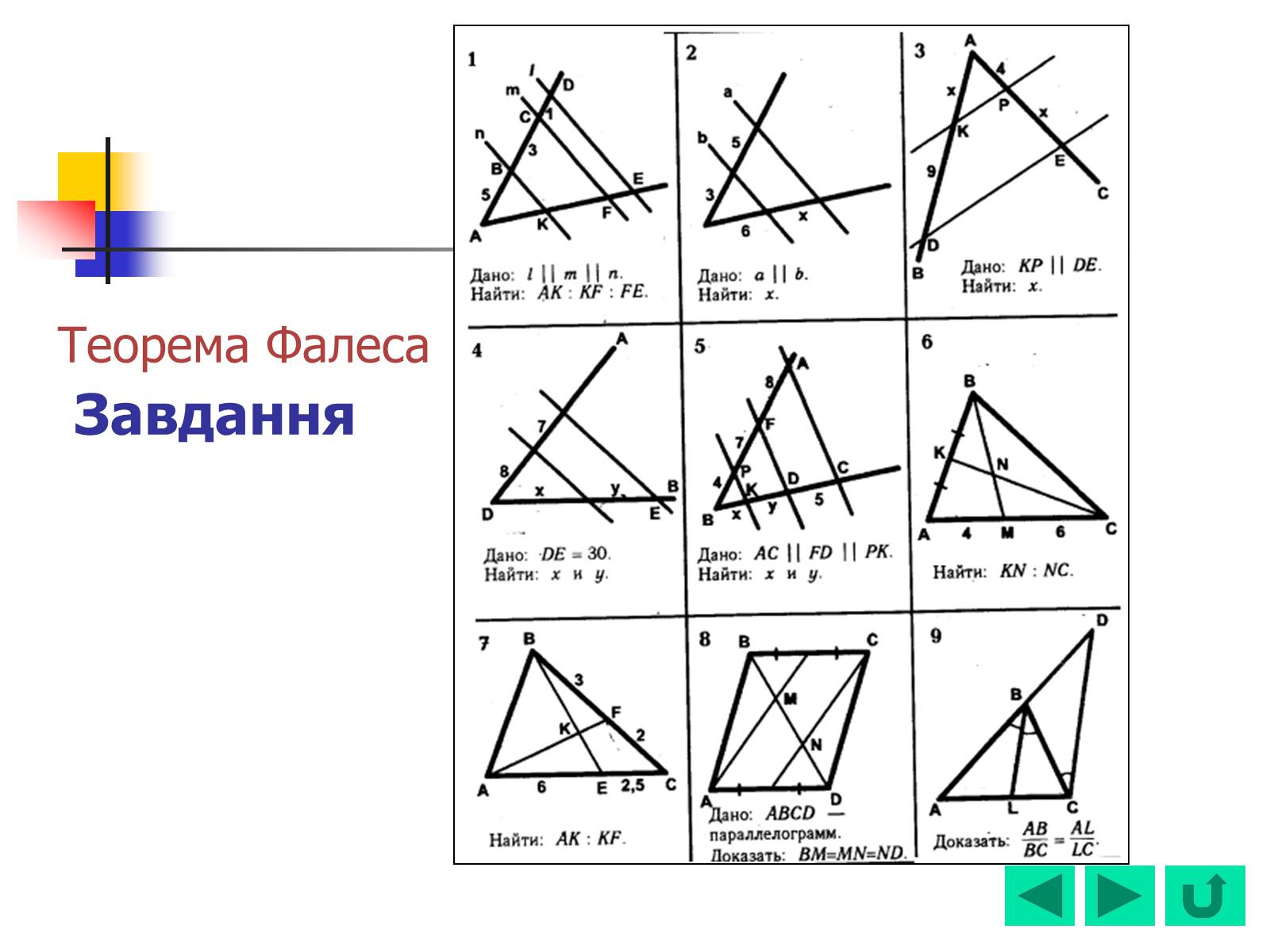
Слайд #35
Теорема Фалеса Завдання
Слайд #36
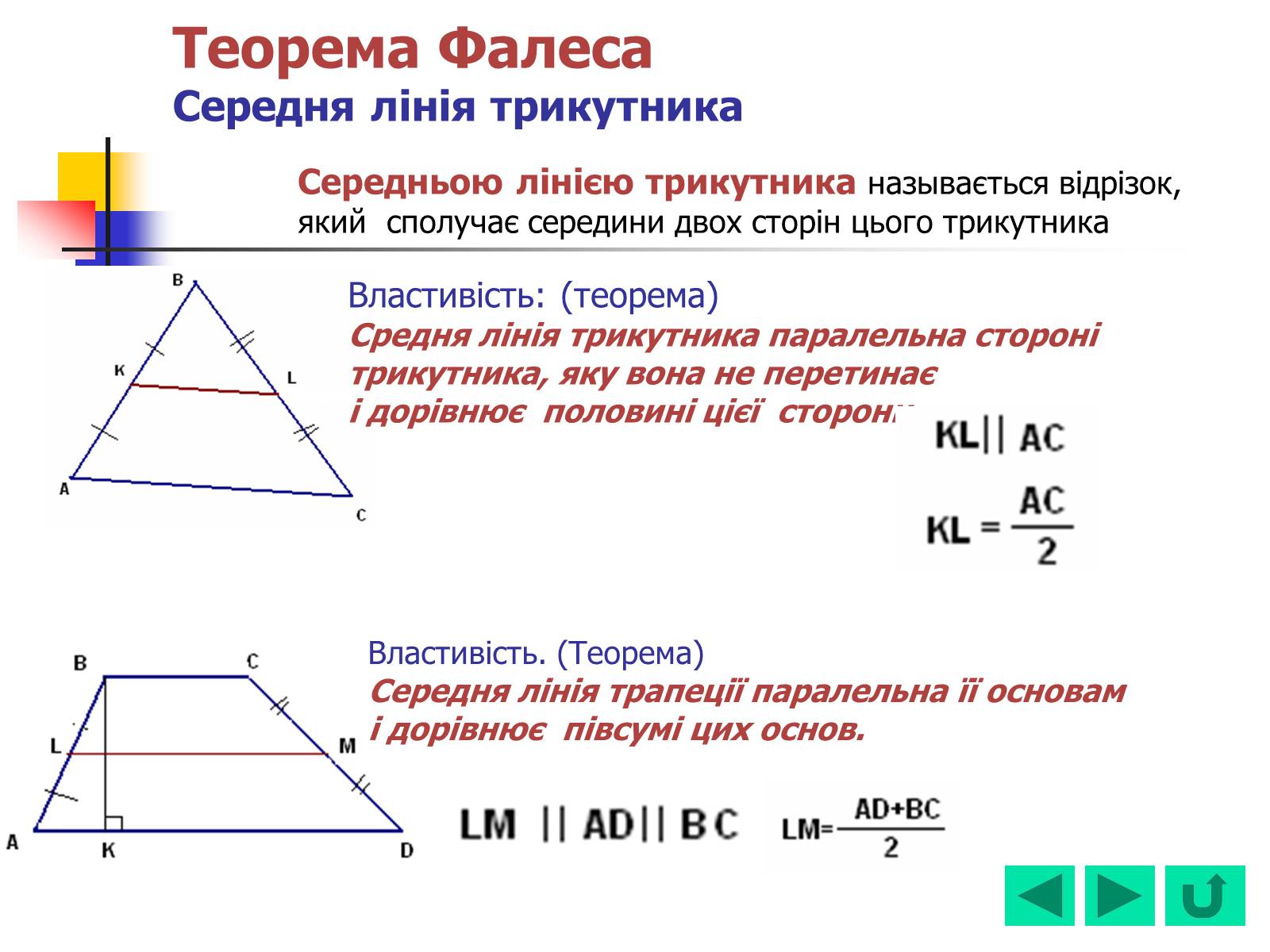
Теорема ФалесаСередня лінія трикутника
Середньою лінією трикутника называється відрізок,
який сполучає середини двох сторін цього трикутника
Властивість: (теорема)
Средня лінія трикутника паралельна стороні
трикутника, яку вона не перетинає
і дорівнює половині цієї сторони.
Властивість. (Теорема)
Середня лінія трапеції паралельна її основам
і дорівнює півсумі цих основ.
Середньою лінією трикутника называється відрізок,
який сполучає середини двох сторін цього трикутника
Властивість: (теорема)
Средня лінія трикутника паралельна стороні
трикутника, яку вона не перетинає
і дорівнює половині цієї сторони.
Властивість. (Теорема)
Середня лінія трапеції паралельна її основам
і дорівнює півсумі цих основ.
Слайд #37
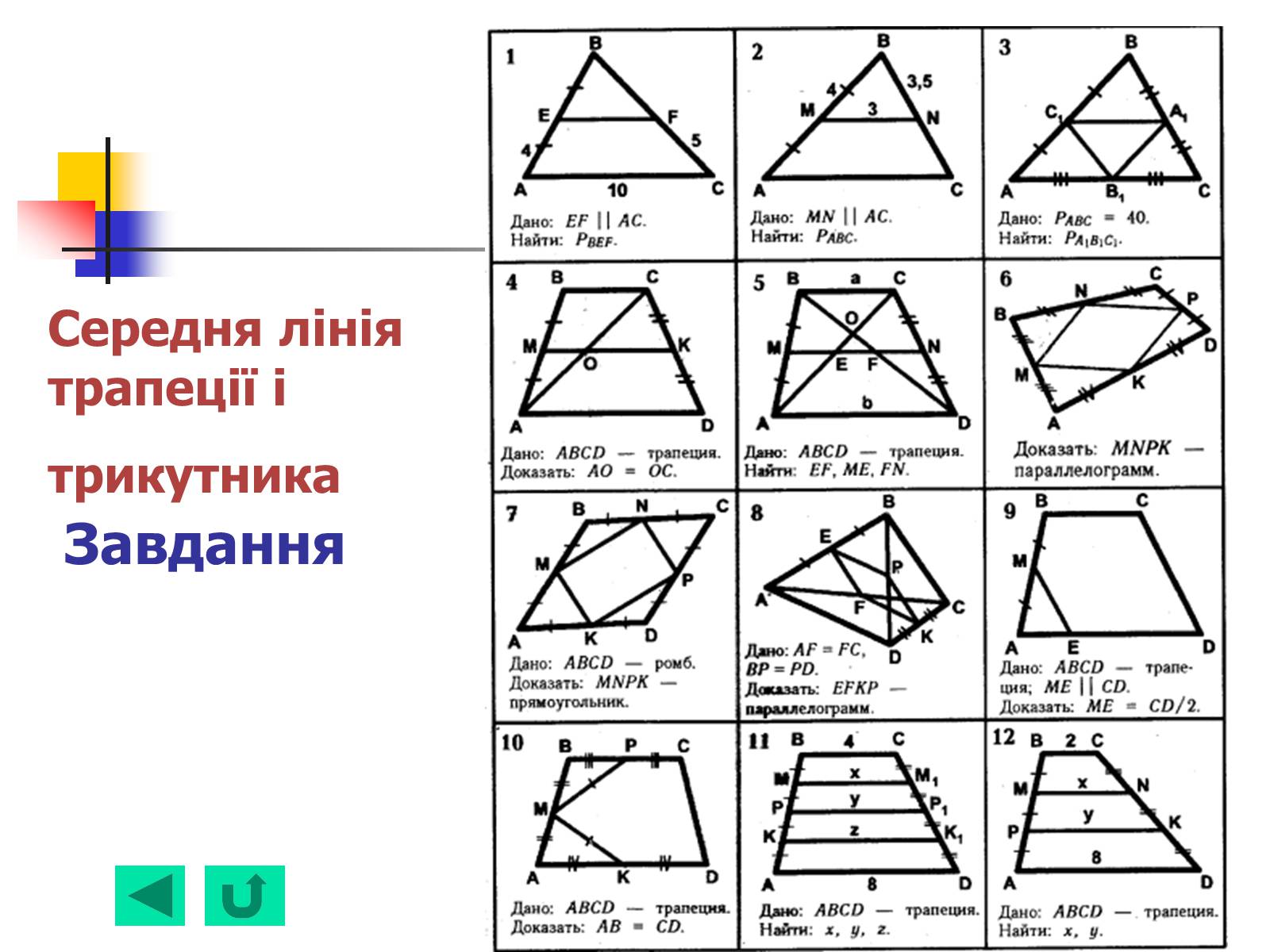
Середня лінія трапеції і трикутника Завдання
Слайд #38
Узагальнена теорема Фалеса
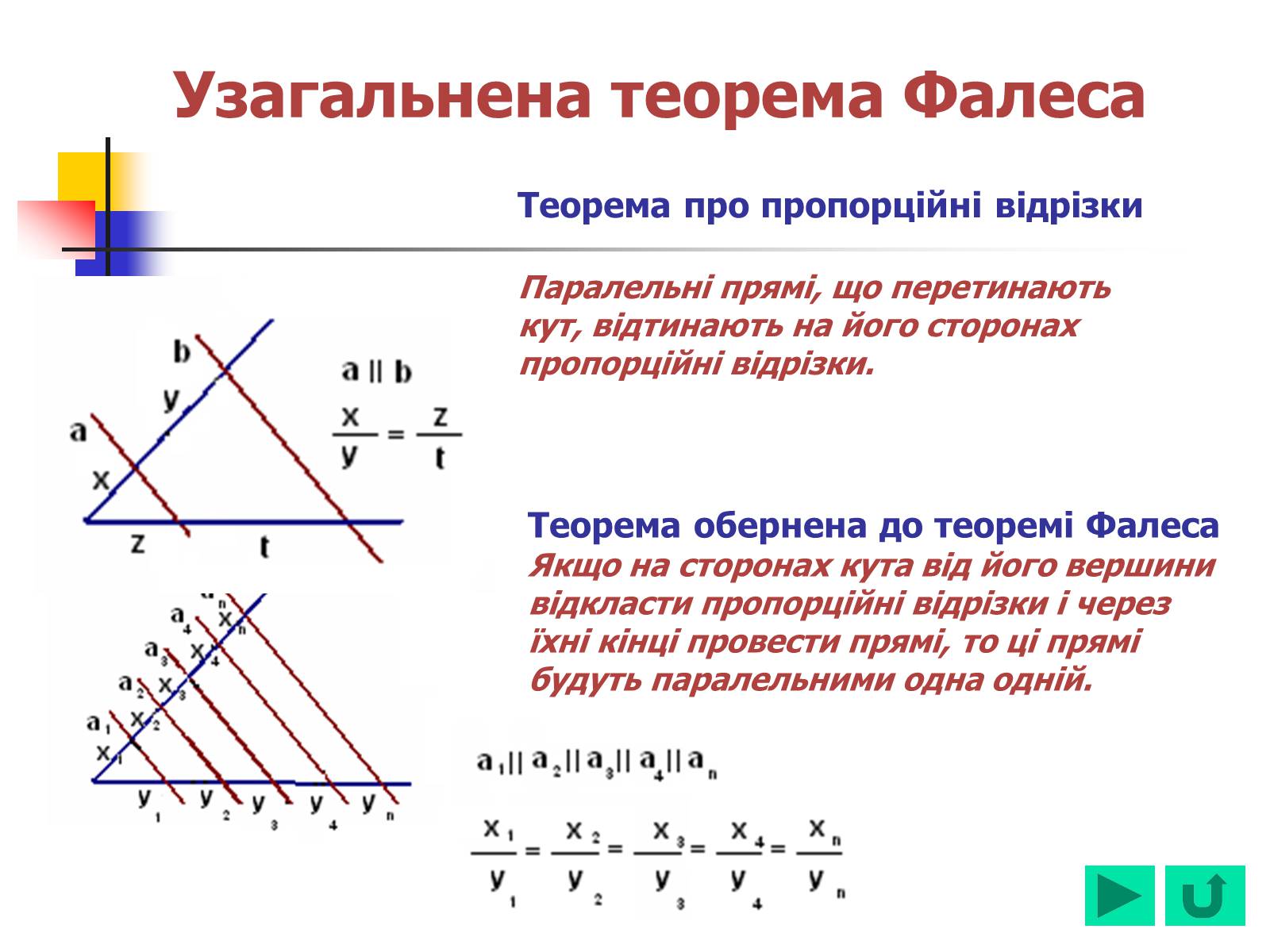
Теорема про пропорційні відрізки
Паралельні прямі, що перетинають кут, відтинають на його сторонах пропорційні відрізки.
Теорема обернена до теоремі Фалеса
Якщо на сторонах кута від його вершини відкласти пропорційні відрізки і через їхні кінці провести прямі, то ці прямі будуть паралельними одна одній.
Теорема про пропорційні відрізки
Паралельні прямі, що перетинають кут, відтинають на його сторонах пропорційні відрізки.
Теорема обернена до теоремі Фалеса
Якщо на сторонах кута від його вершини відкласти пропорційні відрізки і через їхні кінці провести прямі, то ці прямі будуть паралельними одна одній.
Слайд #39
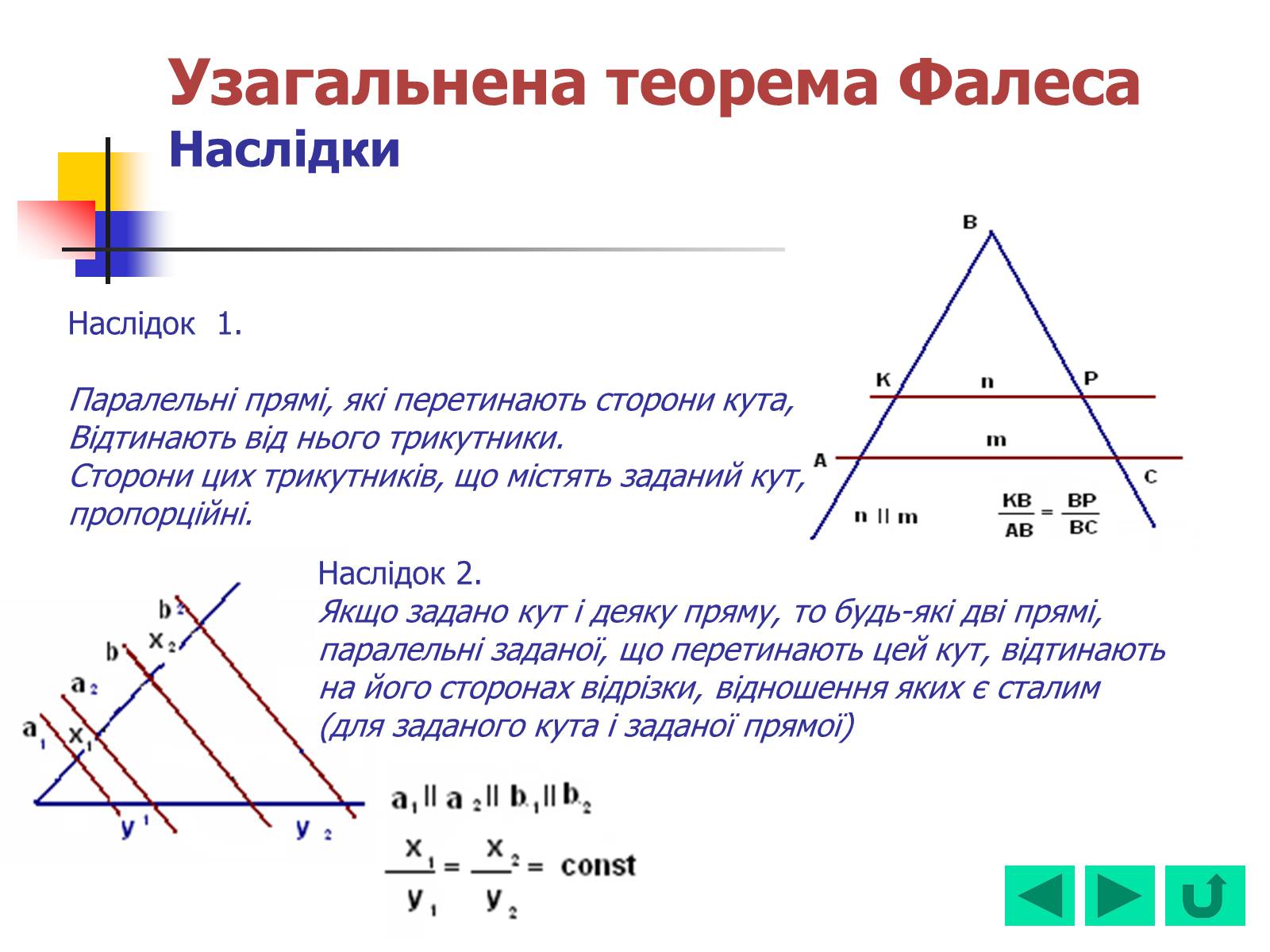
Наслідок 1.
Паралельні прямі, які перетинають сторони кута,
Відтинають від нього трикутники.
Сторони цих трикутників, що містять заданий кут,
пропорційні.
Наслідок 2.
Якщо задано кут і деяку пряму, то будь-які дві прямі, паралельні заданої, що перетинають цей кут, відтинають на його сторонах відрізки, відношення яких є сталим (для заданого кута і заданої прямої)
Узагальнена теорема Фалеса Наслідки
Паралельні прямі, які перетинають сторони кута,
Відтинають від нього трикутники.
Сторони цих трикутників, що містять заданий кут,
пропорційні.
Наслідок 2.
Якщо задано кут і деяку пряму, то будь-які дві прямі, паралельні заданої, що перетинають цей кут, відтинають на його сторонах відрізки, відношення яких є сталим (для заданого кута і заданої прямої)
Узагальнена теорема Фалеса Наслідки
Слайд #40
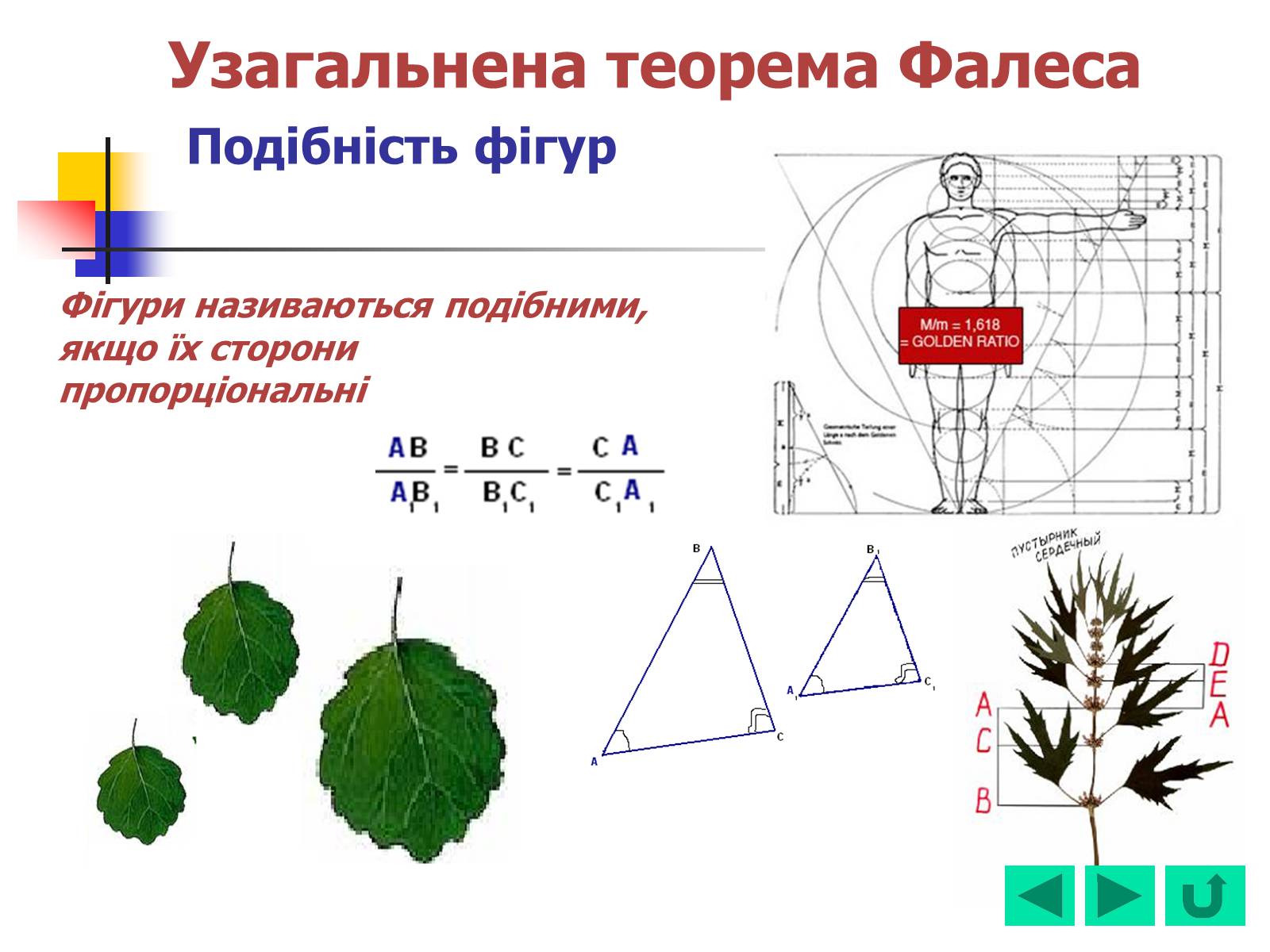
Узагальнена теорема Фалеса Подібність фігур
Фігури називаються подібними, якщо їх сторони
пропорціональні
Фігури називаються подібними, якщо їх сторони
пропорціональні
Слайд #41
Узагальнена теорема ФалесаПодібність трикутників
Два трикутника називаються подібними, якщо в них рівні кути, а проти рівних кутів лежать пропорційні сторони.
Дві сторони подібних трикутників, які лежать проти рівних кутів називаються відповідними сторонами.
Вершини равних кутів подібних tтрикутників називаються
відповідними вершинами.
Рівні кути подібних трикутників називаються відповідними кутами.
Трикутники ABC и A1B1C1 подібні.
Відповідні вершини трикутників: A и A1, B и B1, С и С1
Відповідні кути рівні.
Відповідні сторони пропорціональні
Два трикутника називаються подібними, якщо в них рівні кути, а проти рівних кутів лежать пропорційні сторони.
Дві сторони подібних трикутників, які лежать проти рівних кутів називаються відповідними сторонами.
Вершини равних кутів подібних tтрикутників називаються
відповідними вершинами.
Рівні кути подібних трикутників називаються відповідними кутами.
Трикутники ABC и A1B1C1 подібні.
Відповідні вершини трикутників: A и A1, B и B1, С и С1
Відповідні кути рівні.
Відповідні сторони пропорціональні

Слайд #42
Узагальнена теорема Фалеса Подібність трикутників
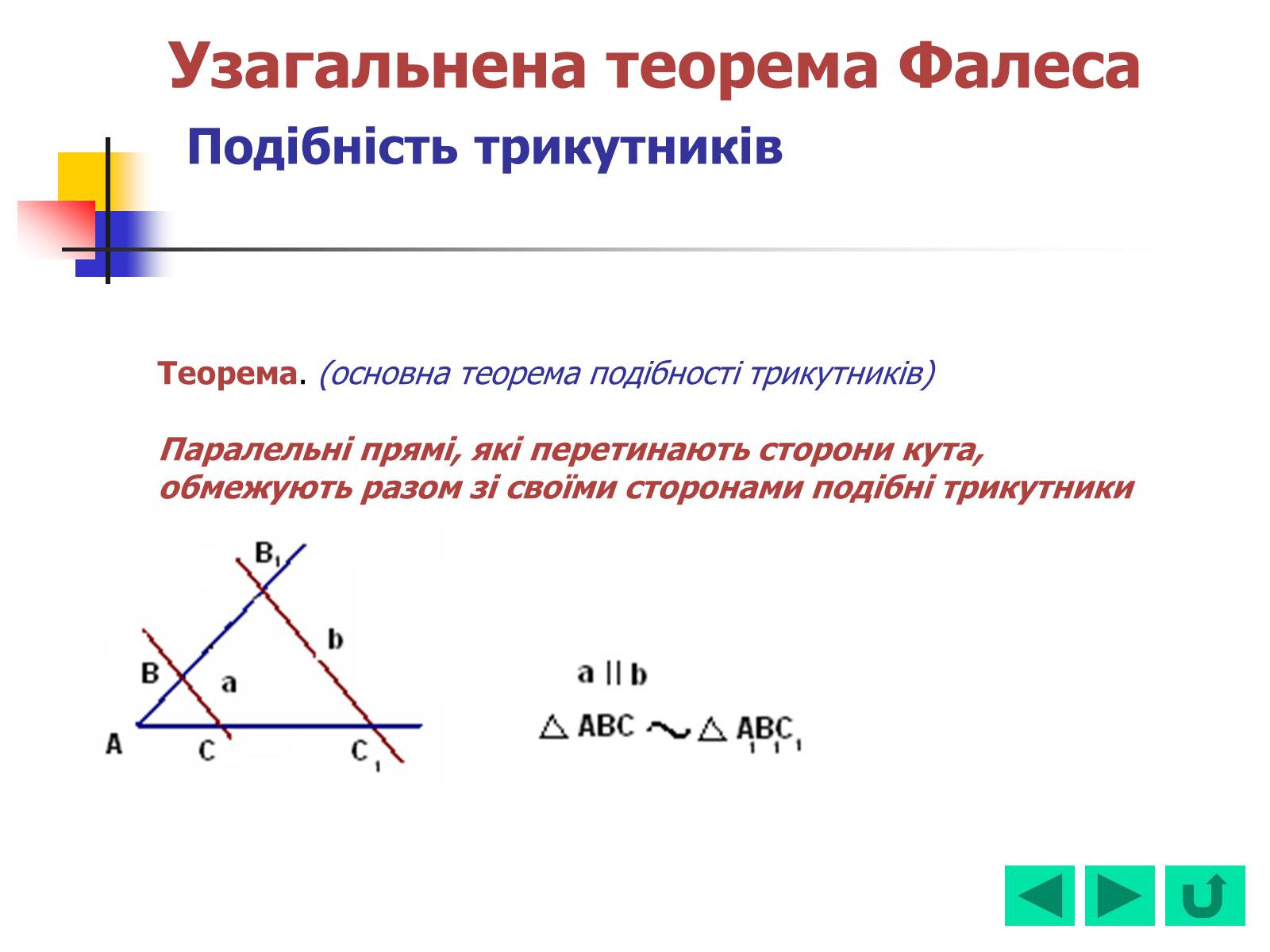
Теорема. (основна теорема подібності трикутників)
Паралельні прямі, які перетинають сторони кута,
обмежують разом зі своїми сторонами подібні трикутники
Теорема. (основна теорема подібності трикутників)
Паралельні прямі, які перетинають сторони кута,
обмежують разом зі своїми сторонами подібні трикутники
Слайд #43
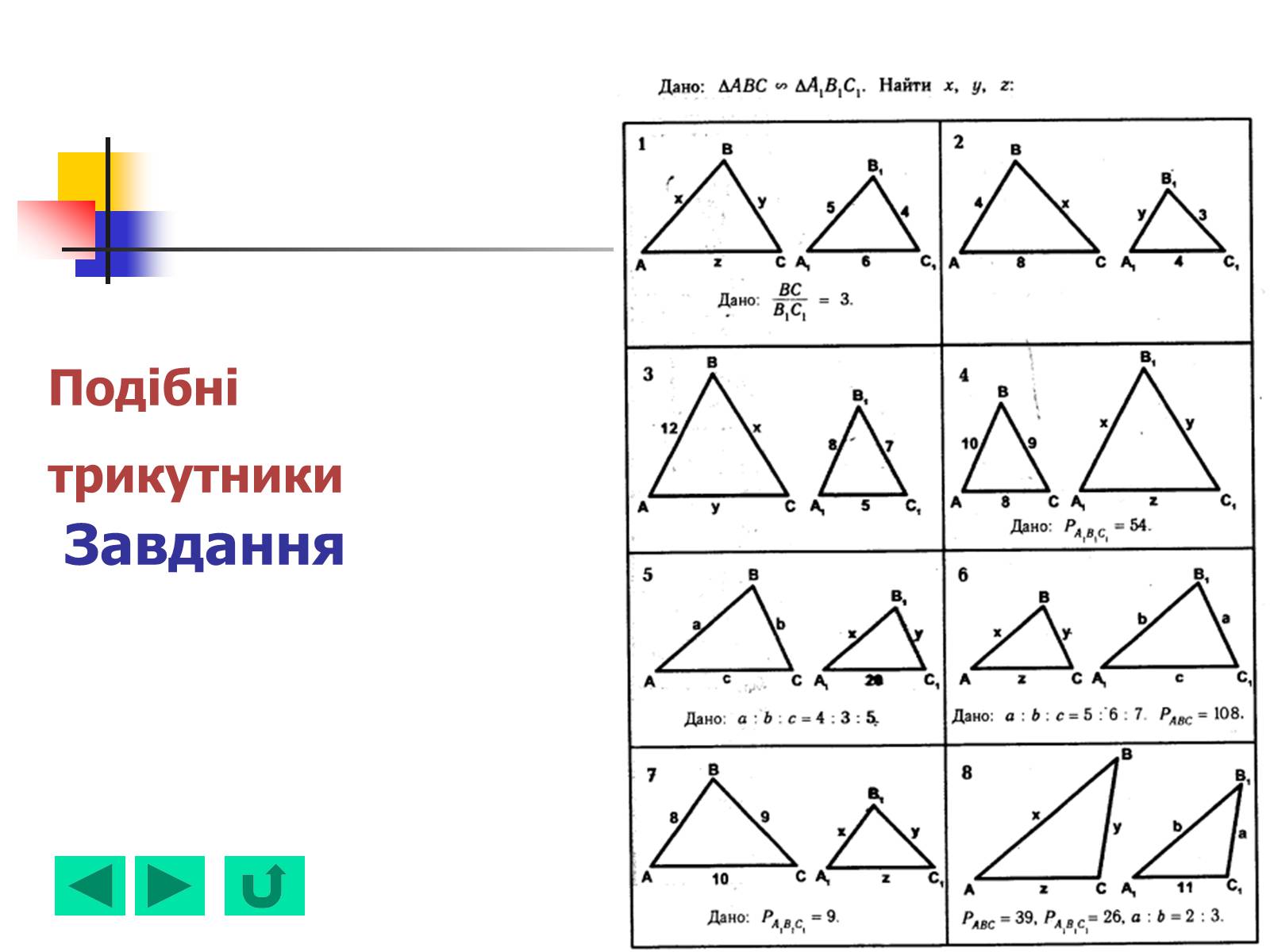
Подібні трикутники Завдання
Слайд #44
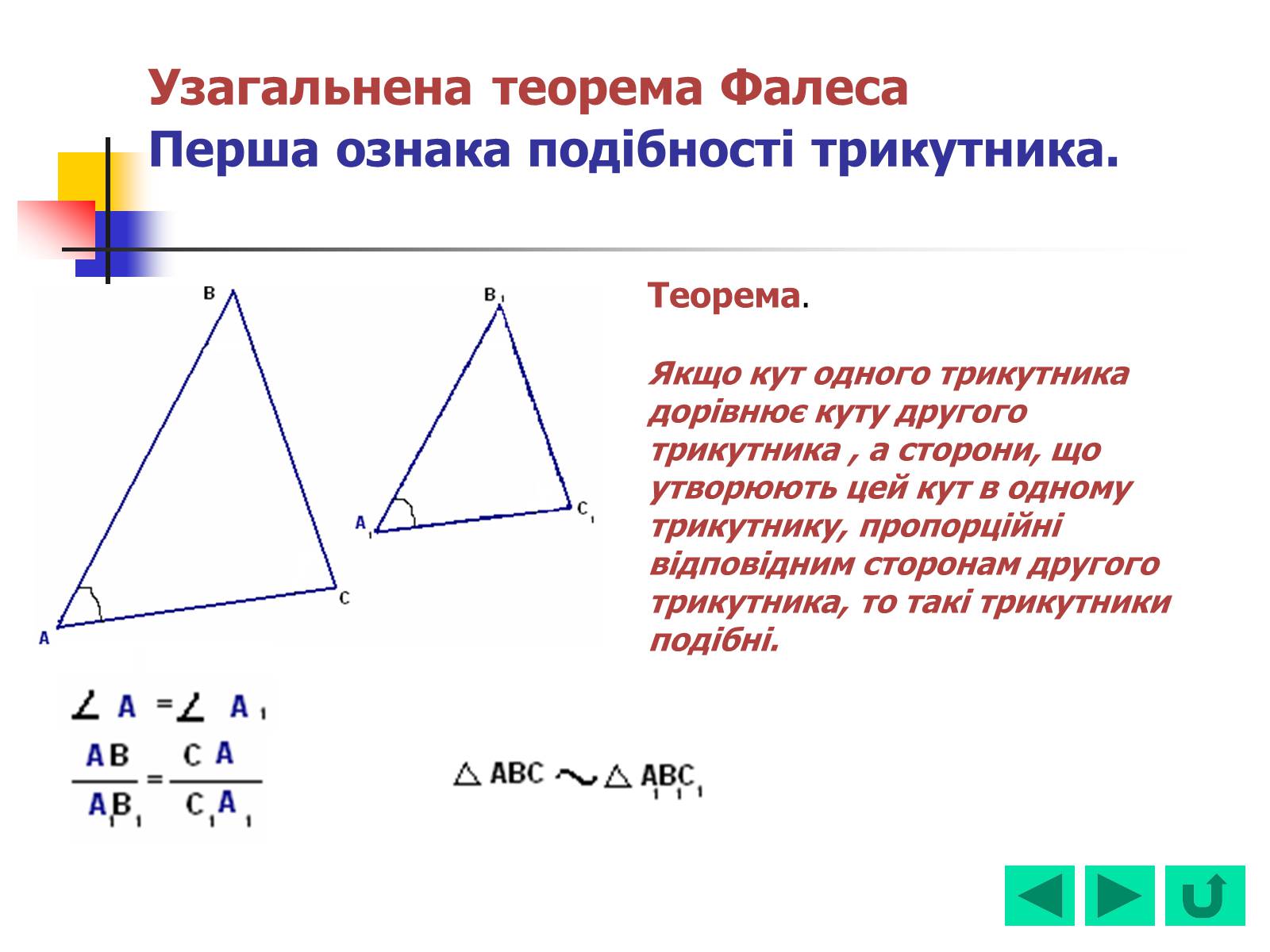
Узагальнена теорема Фалеса Перша ознака подібності трикутника.
Теорема.
Якщо кут одного трикутника дорівнює куту другого трикутника , а сторони, що утворюють цей кут в одному трикутнику, пропорційні відповідним сторонам другого трикутника, то такі трикутники подібні.
Теорема.
Якщо кут одного трикутника дорівнює куту другого трикутника , а сторони, що утворюють цей кут в одному трикутнику, пропорційні відповідним сторонам другого трикутника, то такі трикутники подібні.
Слайд #45
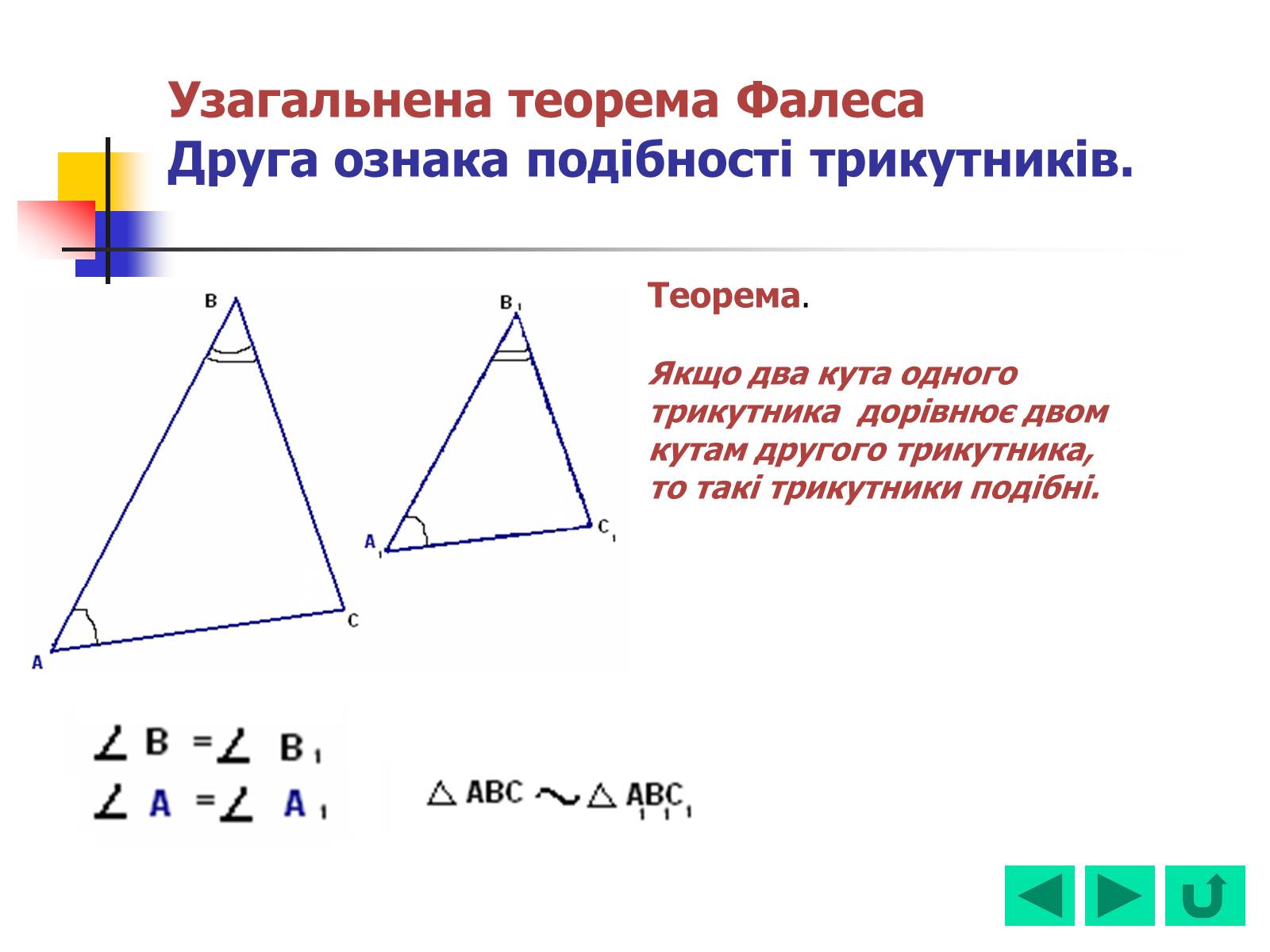
Узагальнена теорема ФалесаДруга ознака подібності трикутників.
Теорема.
Якщо два кута одного трикутника дорівнює двом кутам другого трикутника,
то такі трикутники подібні.
Теорема.
Якщо два кута одного трикутника дорівнює двом кутам другого трикутника,
то такі трикутники подібні.
Слайд #46
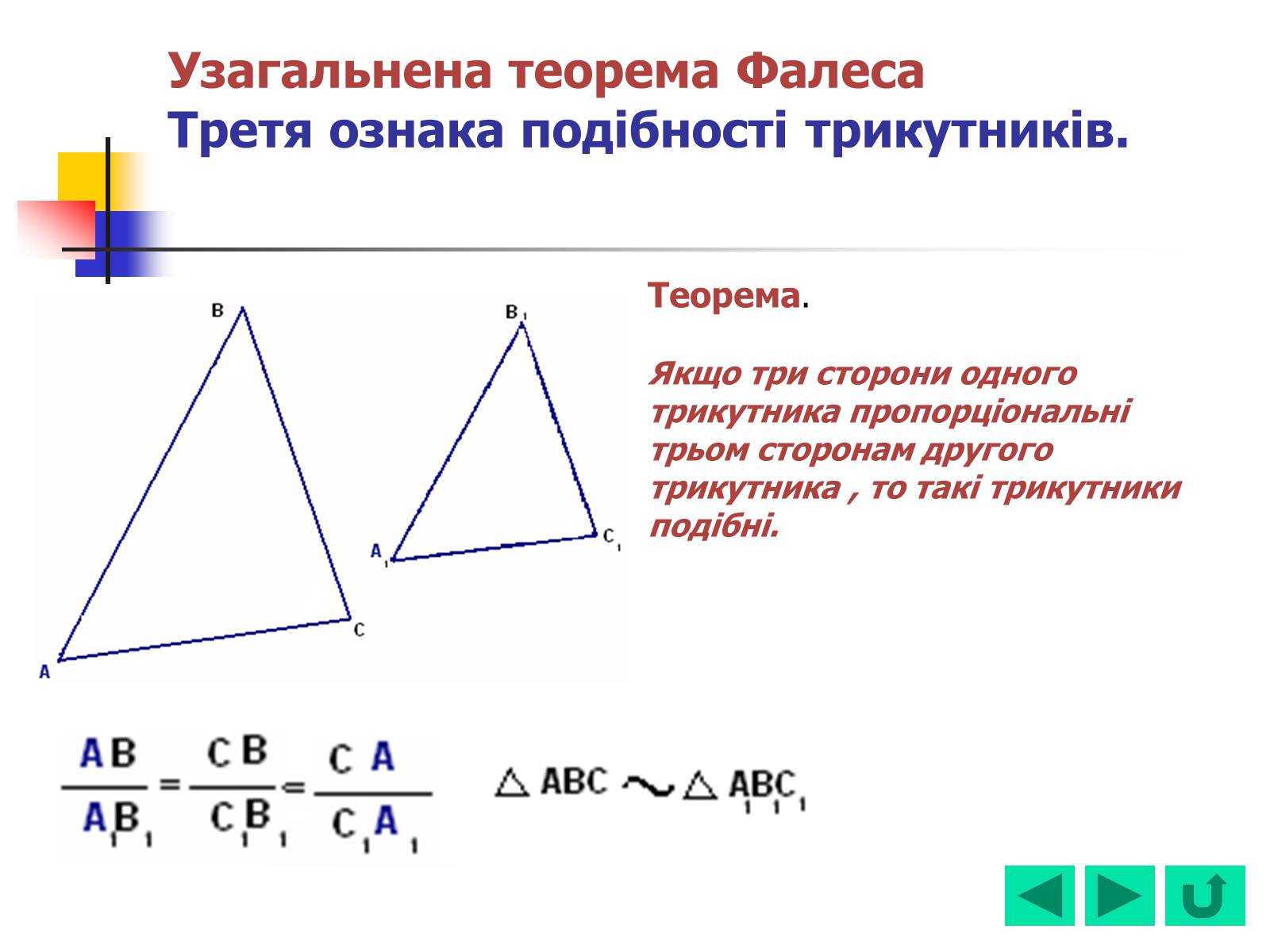
Узагальнена теорема ФалесаТретя ознака подібності трикутників.
Теорема.
Якщо три сторони одного трикутника пропорціональні трьом сторонам другого трикутника , то такі трикутники подібні.
Теорема.
Якщо три сторони одного трикутника пропорціональні трьом сторонам другого трикутника , то такі трикутники подібні.
Слайд #47
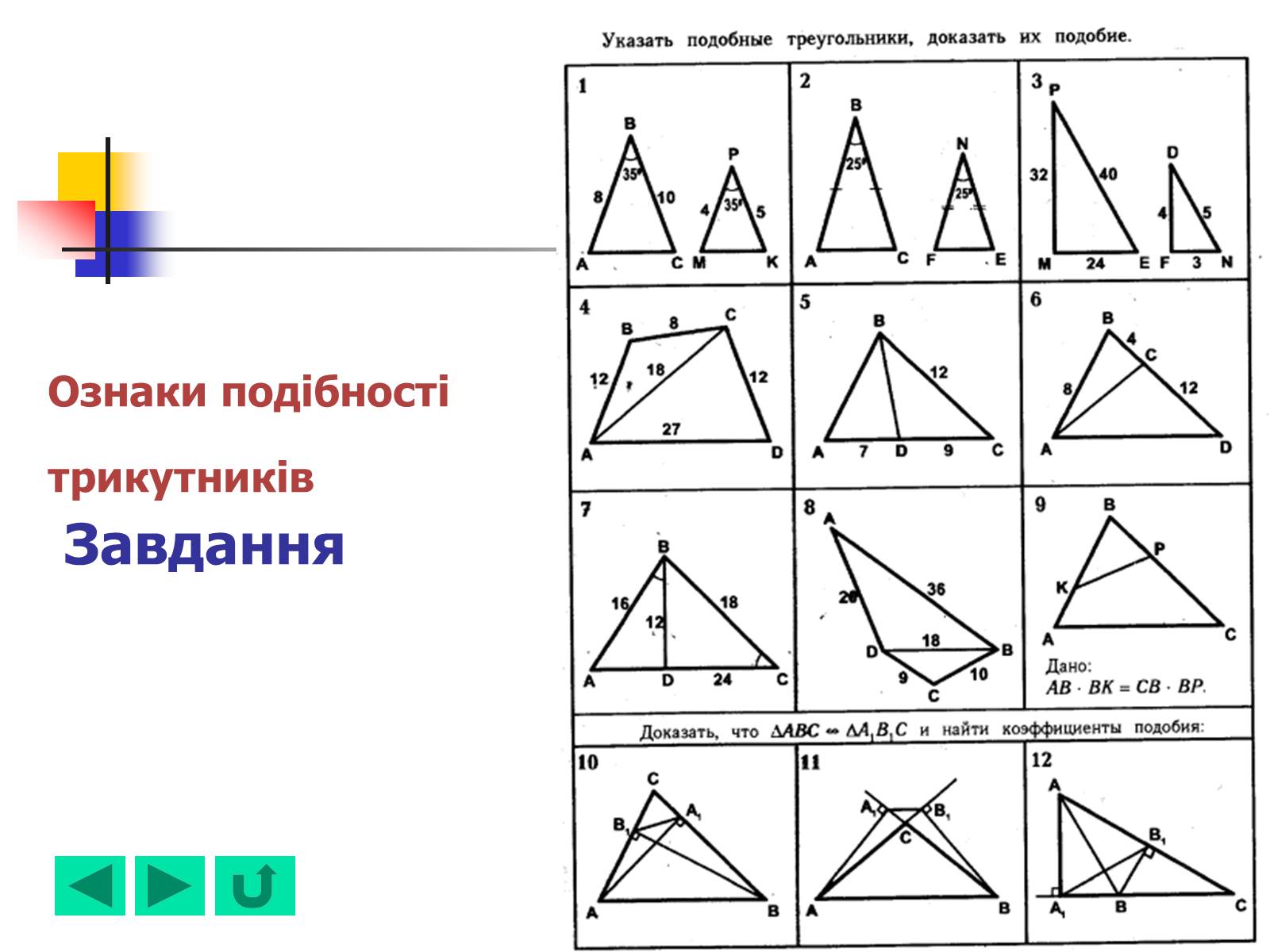
Ознаки подібності трикутників Завдання
Слайд #48
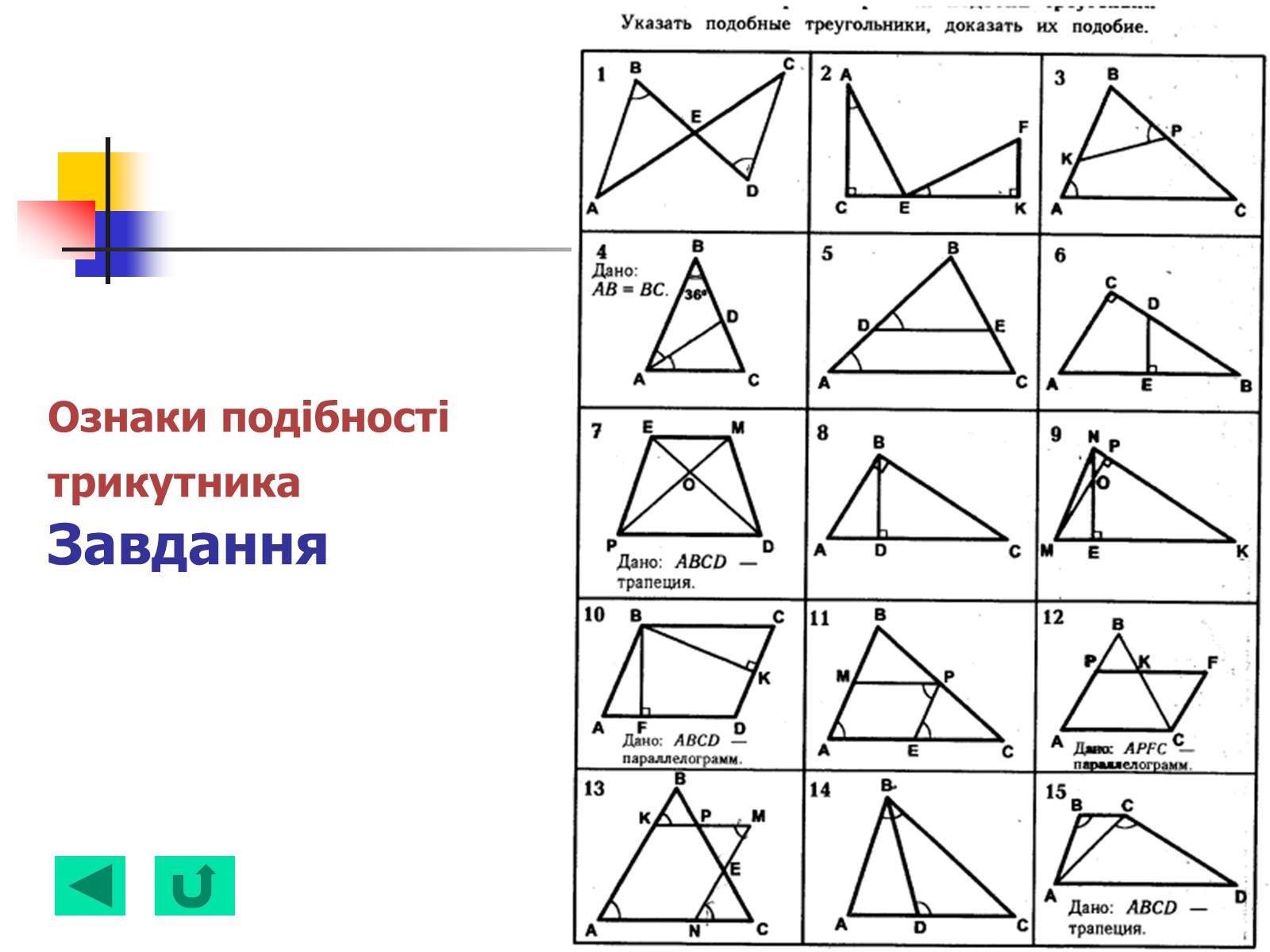
Ознаки подібності трикутника Завдання
Слайд #49
Метрічні співвідношення в прямокутному трикутнику.
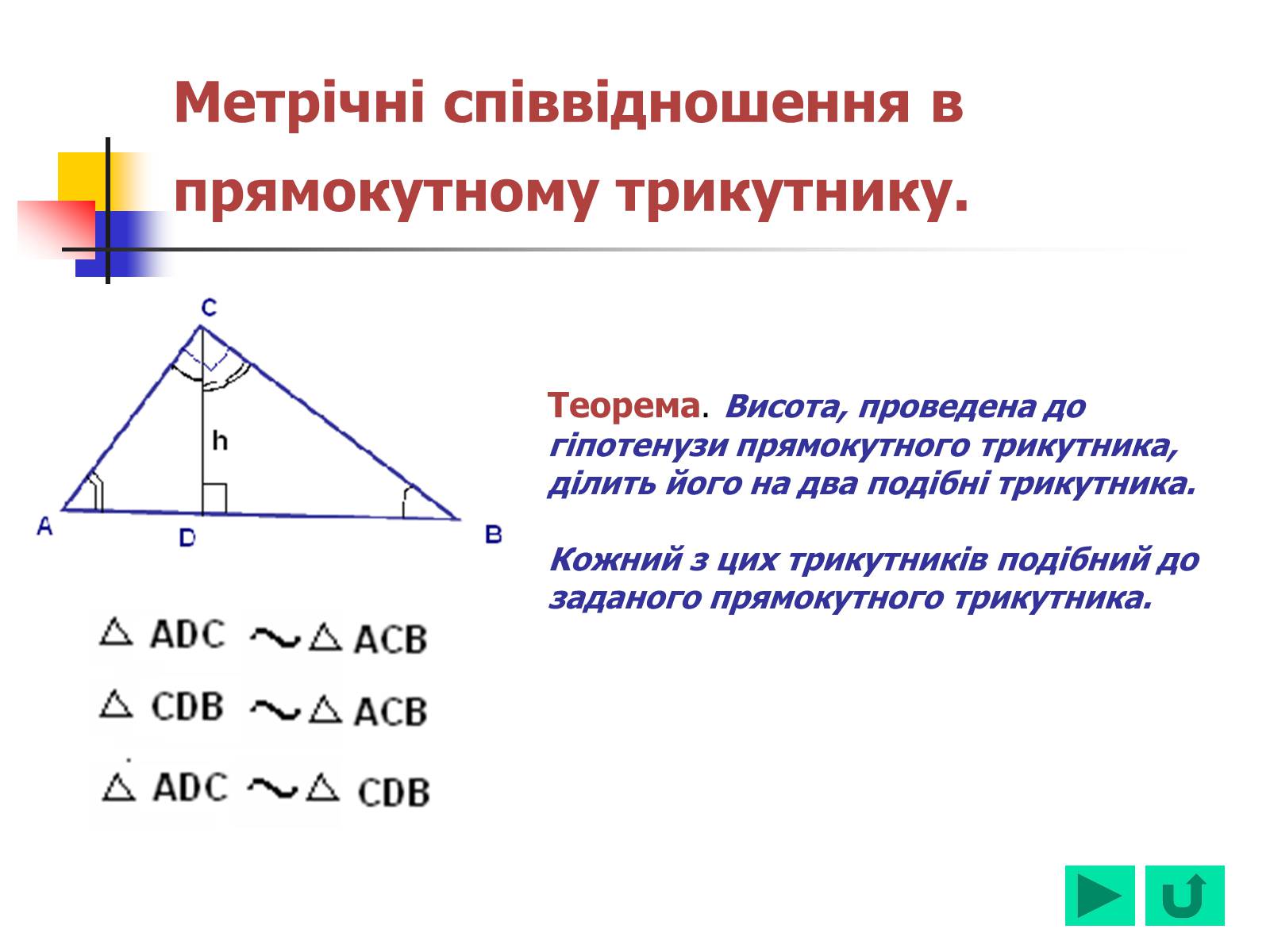
Теорема. Висота, проведена до гіпотенузи прямокутного трикутника, ділить його на два подібні трикутника.
Кожний з цих трикутників подібний до заданого прямокутного трикутника.
Теорема. Висота, проведена до гіпотенузи прямокутного трикутника, ділить його на два подібні трикутника.
Кожний з цих трикутників подібний до заданого прямокутного трикутника.
Слайд #50
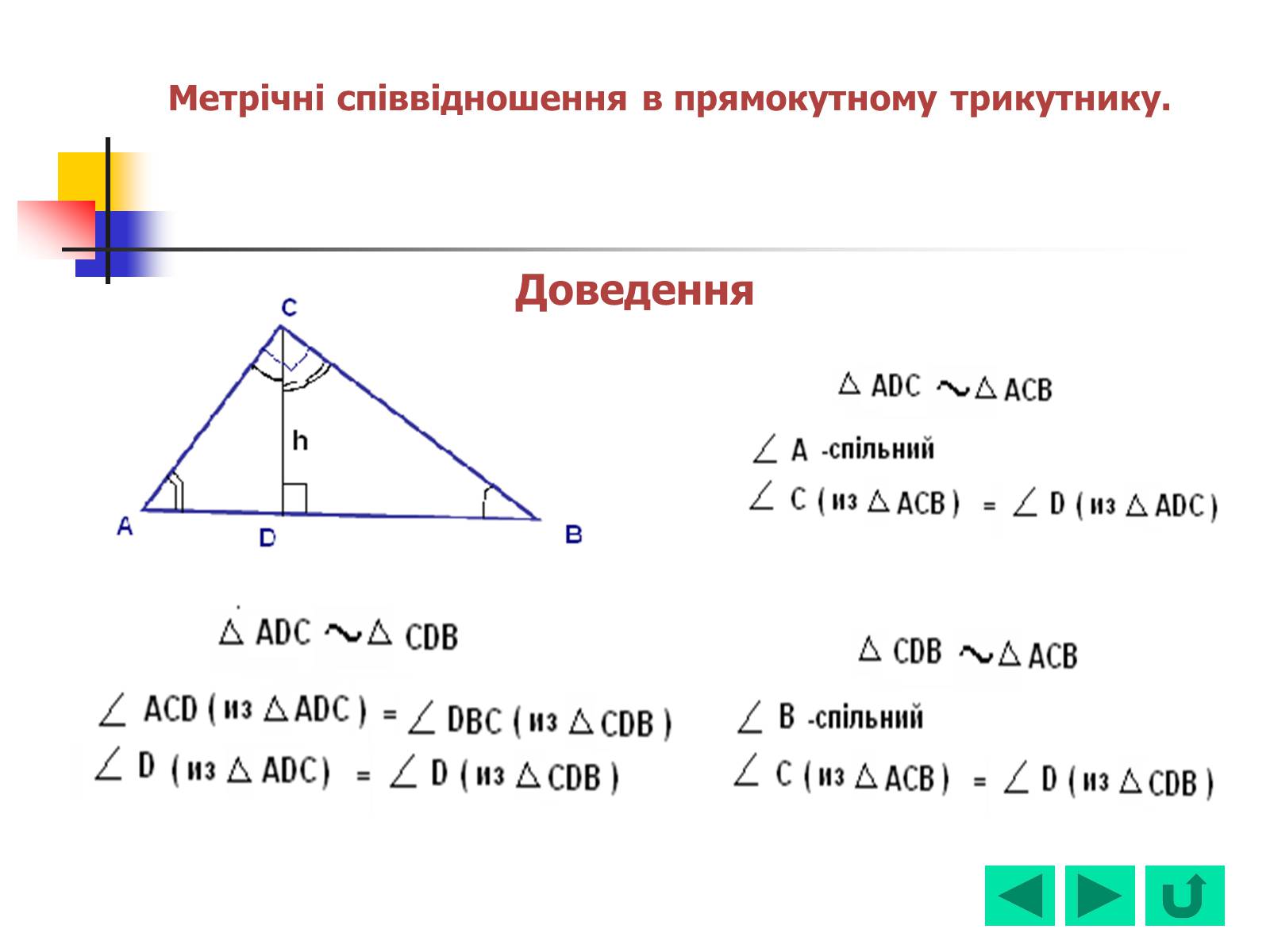
Доведення
Метрічні співвідношення в прямокутному трикутнику.
Метрічні співвідношення в прямокутному трикутнику.
Слайд #51
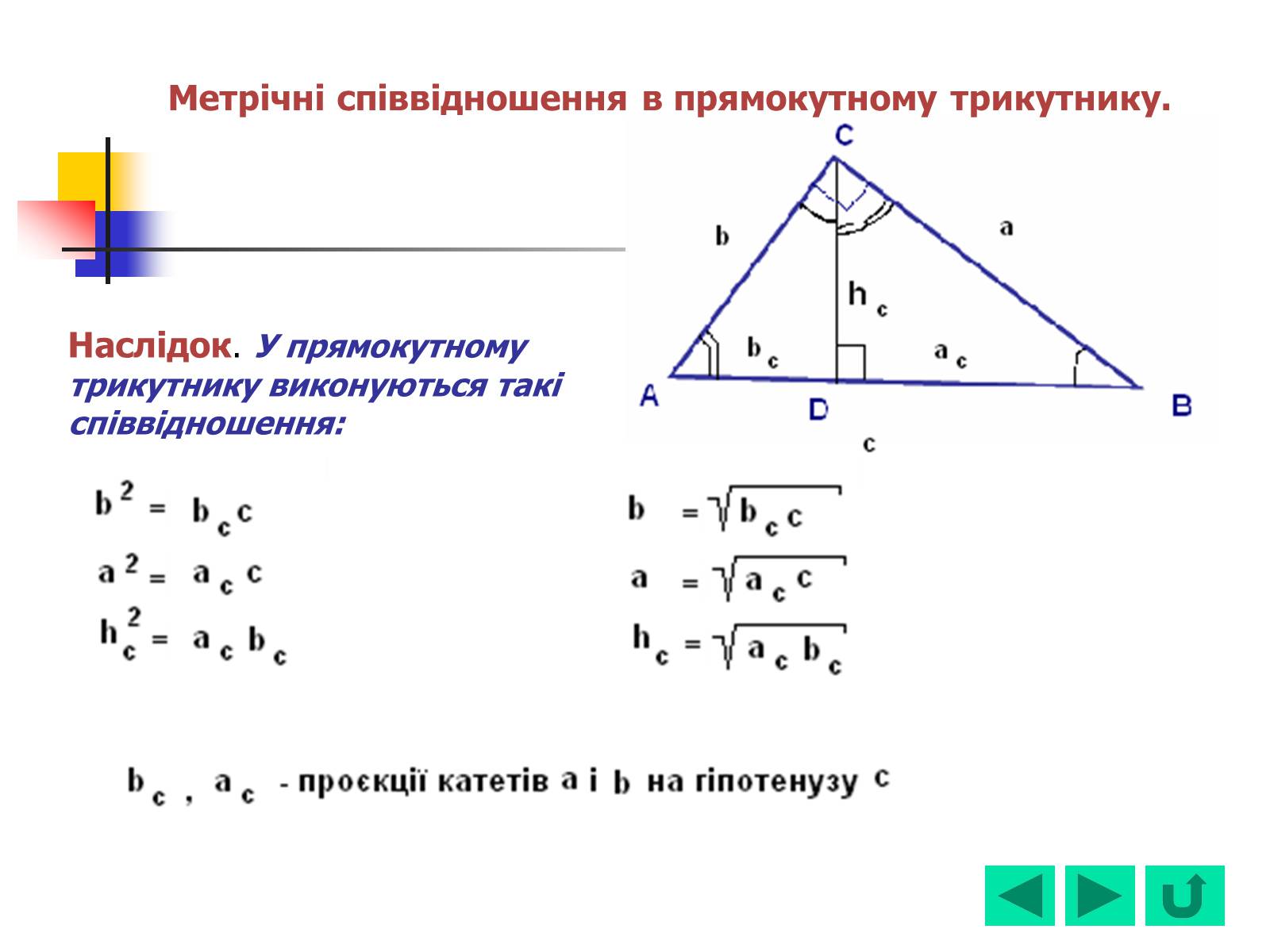
Наслідок. У прямокутному трикутнику виконуються такі співвідношення:
Метрічні співвідношення в прямокутному трикутнику.
Метрічні співвідношення в прямокутному трикутнику.
Слайд #52
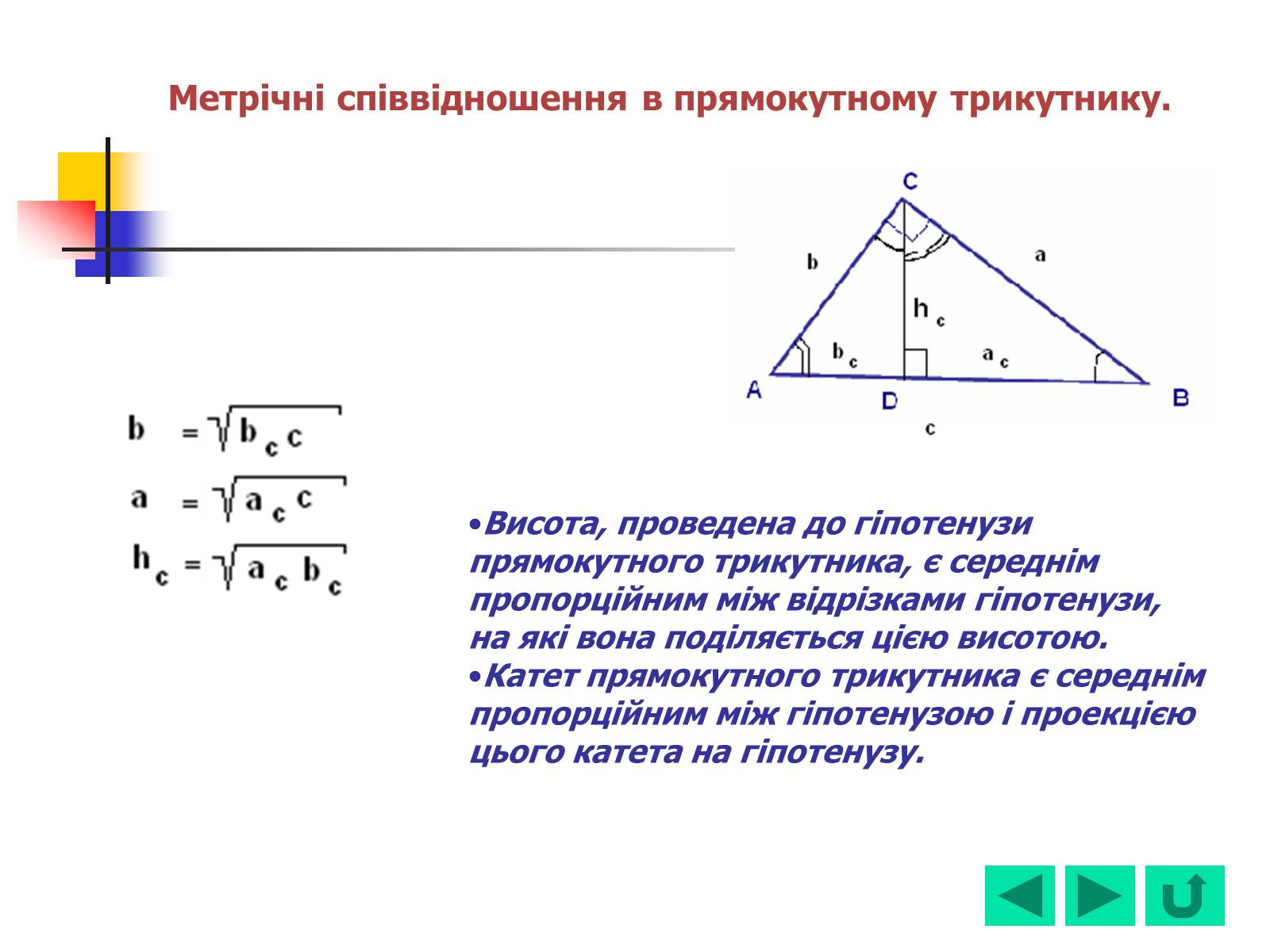
Висота, проведена до гіпотенузи прямокутного трикутника, є середнім пропорційним між відрізками гіпотенузи, на які вона поділяється цією висотою.
Катет прямокутного трикутника є середнім пропорційним між гіпотенузою і проекцією цього катета на гіпотенузу.
Метрічні співвідношення в прямокутному трикутнику.
Катет прямокутного трикутника є середнім пропорційним між гіпотенузою і проекцією цього катета на гіпотенузу.
Метрічні співвідношення в прямокутному трикутнику.
Слайд #53
Теорема 1. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів:
Теорема 2 (обернена). Якщо у трикутника зі сторонами а, в, с виконується рівність
То такий трикутник прямокутний, у якому а та в – катети, с – гіпотенуза.
Метрічні співвідношення в прямокутному трикутнику.
Теорема 2 (обернена). Якщо у трикутника зі сторонами а, в, с виконується рівність
То такий трикутник прямокутний, у якому а та в – катети, с – гіпотенуза.
Метрічні співвідношення в прямокутному трикутнику.

Слайд #54
Наслідок: Трикутник зі сторонами 3, 4,5 одиниць виміру, - прямокутний.
(Такий трикутник називають єгипетським)
Властивість єгипетського трикутника використовувався для розподілу плідних земель вздовж річки Ніл.
(Такий трикутник називають єгипетським)
Властивість єгипетського трикутника використовувався для розподілу плідних земель вздовж річки Ніл.