Презентація на тему «Перпендикулярність прямих і площин у просторі»

Презентація “ Перпендикулярність прямих і площин у просторі ”
Підготувала:
Учениця 10 класу
Прилуцької ЗОШ І-ІІІ ст. №13
Імені Святителя Іоасафа Бєлгородського

Я думаю, що ми ще ніколи не жилив такий геометричний період.Усе навколо – геометрія.Ле Корбюзьє

Переглянувши дану презентацію, ви дізнаєтеся :
Яка відмінність між властивостями перпендикулярних прямих на площині й у просторі;
як побудувати пряму, перпендикулярну до деякої площини простору;
як використовувати ознаки перпендикулярності прямих при розв'язуванні задач ;
як застосовувати ознаку перпендикулярності площин для знаходження довжини відрізка , кінці якого лежать на перпендикулярних прямих;
як пов'язана паралельність та перпендикулярність прямих і площин у просторі;
як порівняти довжини проекцій похилих , маючи довжини похили;
як визначити, чи буде пряма перпендикулярна до похилої або її проекції

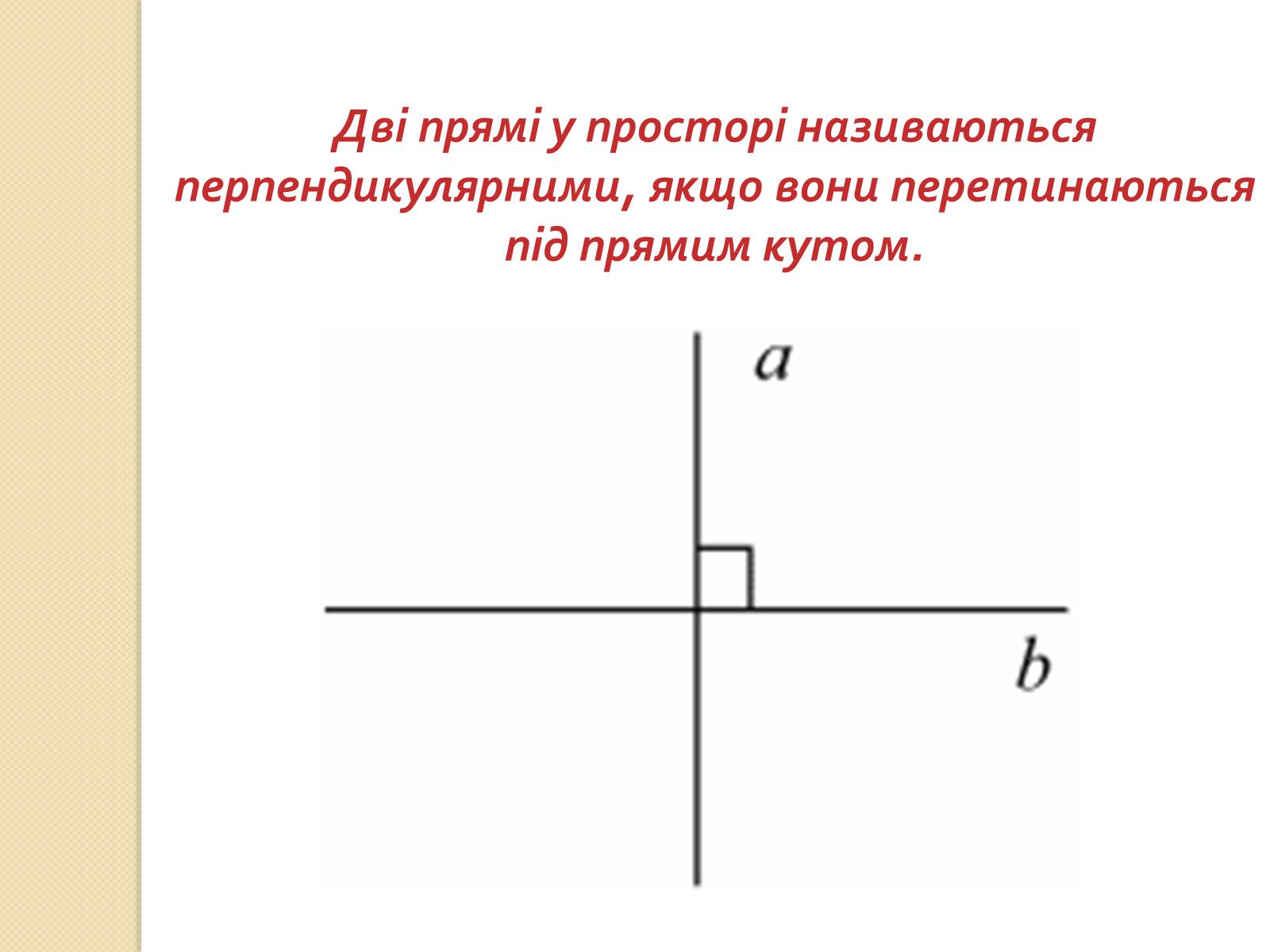
Дві прямі у просторі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

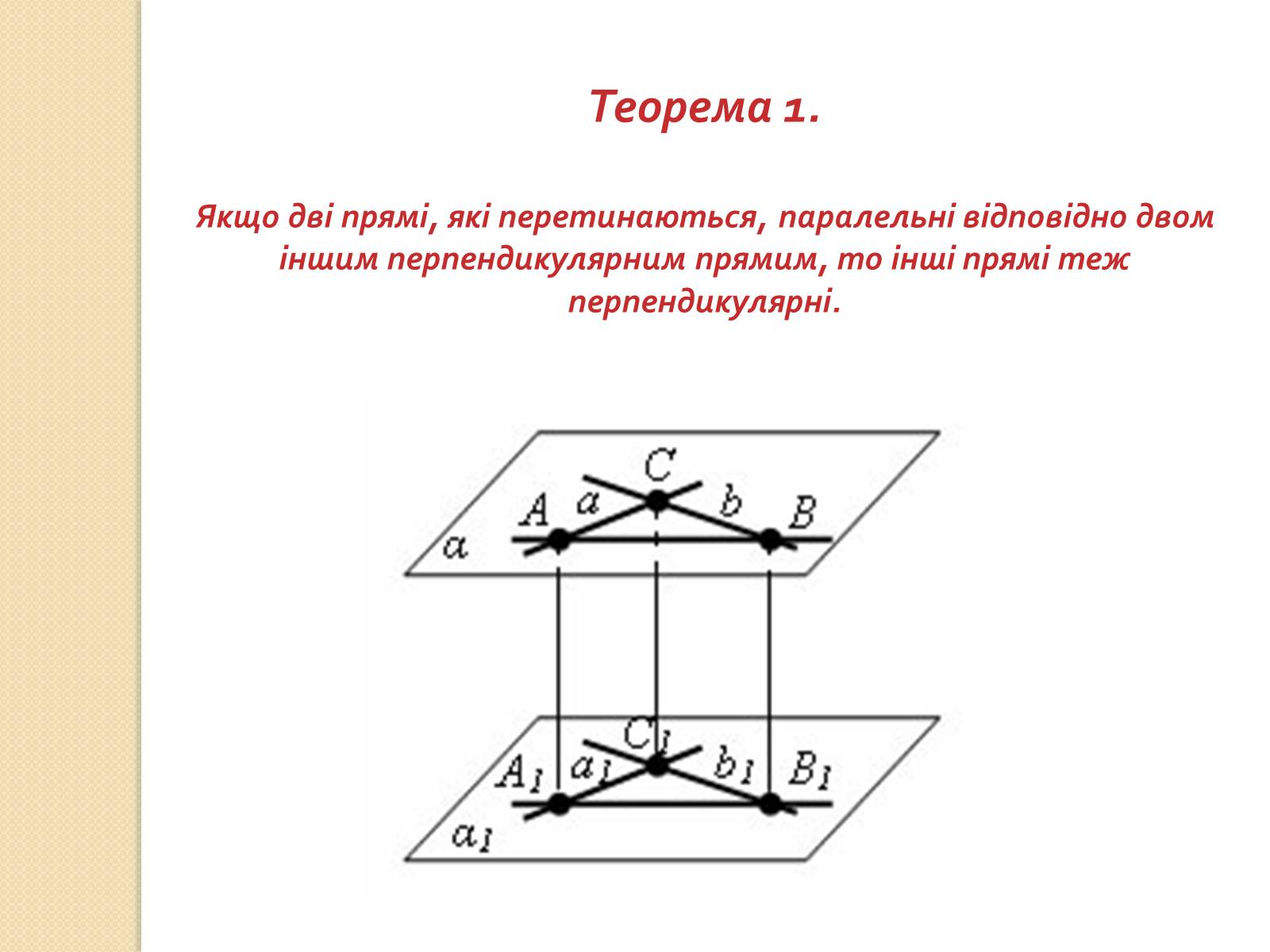
Теорема 1.
Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні.

Теорема 2.
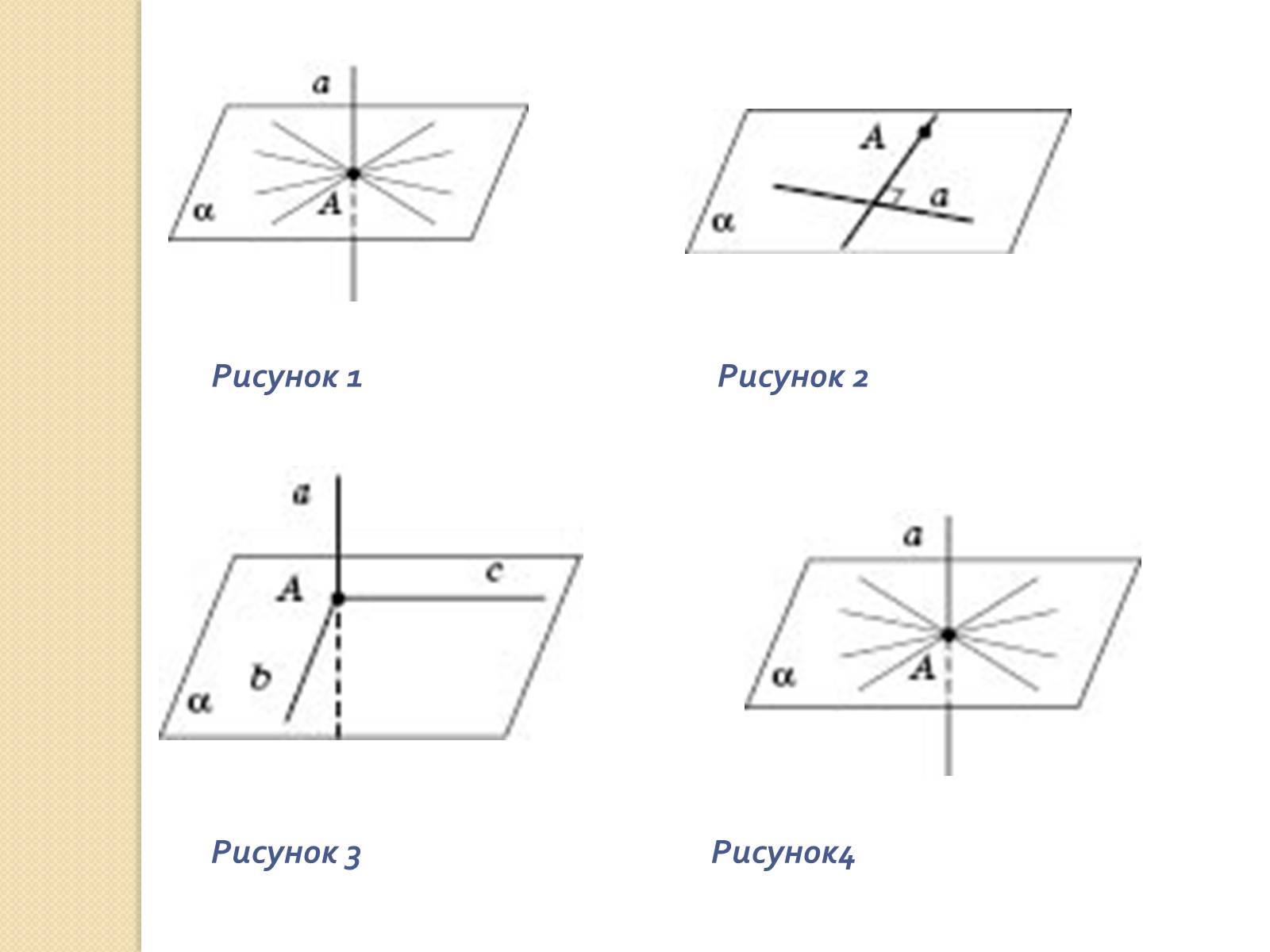
1) Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. Рисунок 1). (Усі прямі лежать у площині, яка перпендикулярна до даної прямої і перетинає її у даній точці.)
2) Через будь-яку точку в просторі, що не належить даній прямій, можна провести пряму, перпендикулярну до даної, і тільки одну. Це буде та перпендикулярна до даної прямої пряма, яка лежить у площині, визначеній даними прямою й точкою (див. Рисунок 2)
3)В просторі дві прямі, перпендикулярні до однієї і тієї самої прямої, не обов'язково паралельні між собою ( див. Рисунок 3)
4) Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину  ( див. Рисунок 4)

Рисунок 1
Рисунок 2
Рисунок 3 Рисунок4

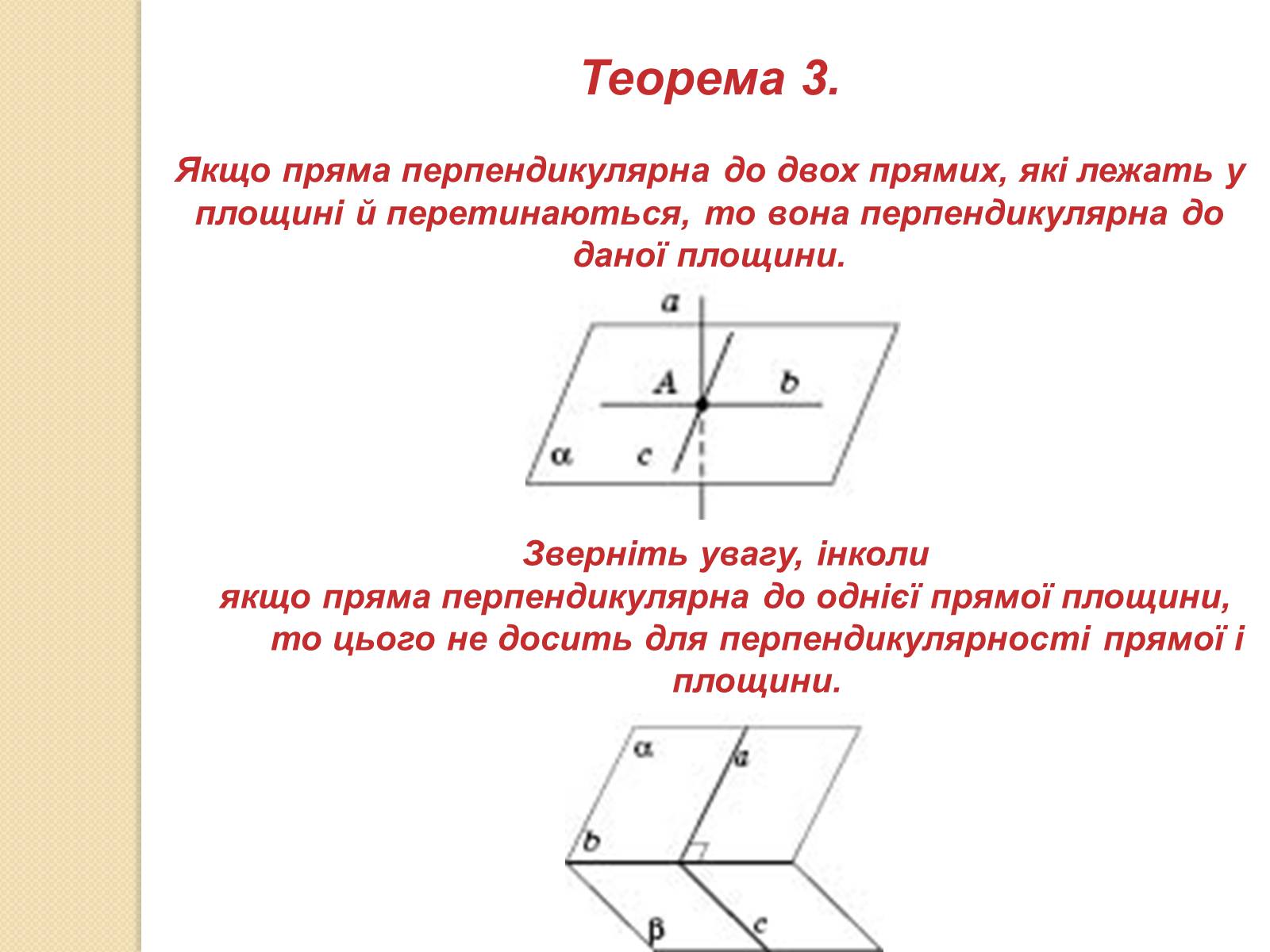
Теорема 3.
Якщо пряма перпендикулярна до двох прямих, які лежать у площині й перетинаються, то вона перпендикулярна до даної площини.
Зверніть увагу, інколи
якщо пряма перпендикулярна до однієї прямої площини, то цього не досить для перпендикулярності прямої і площини.

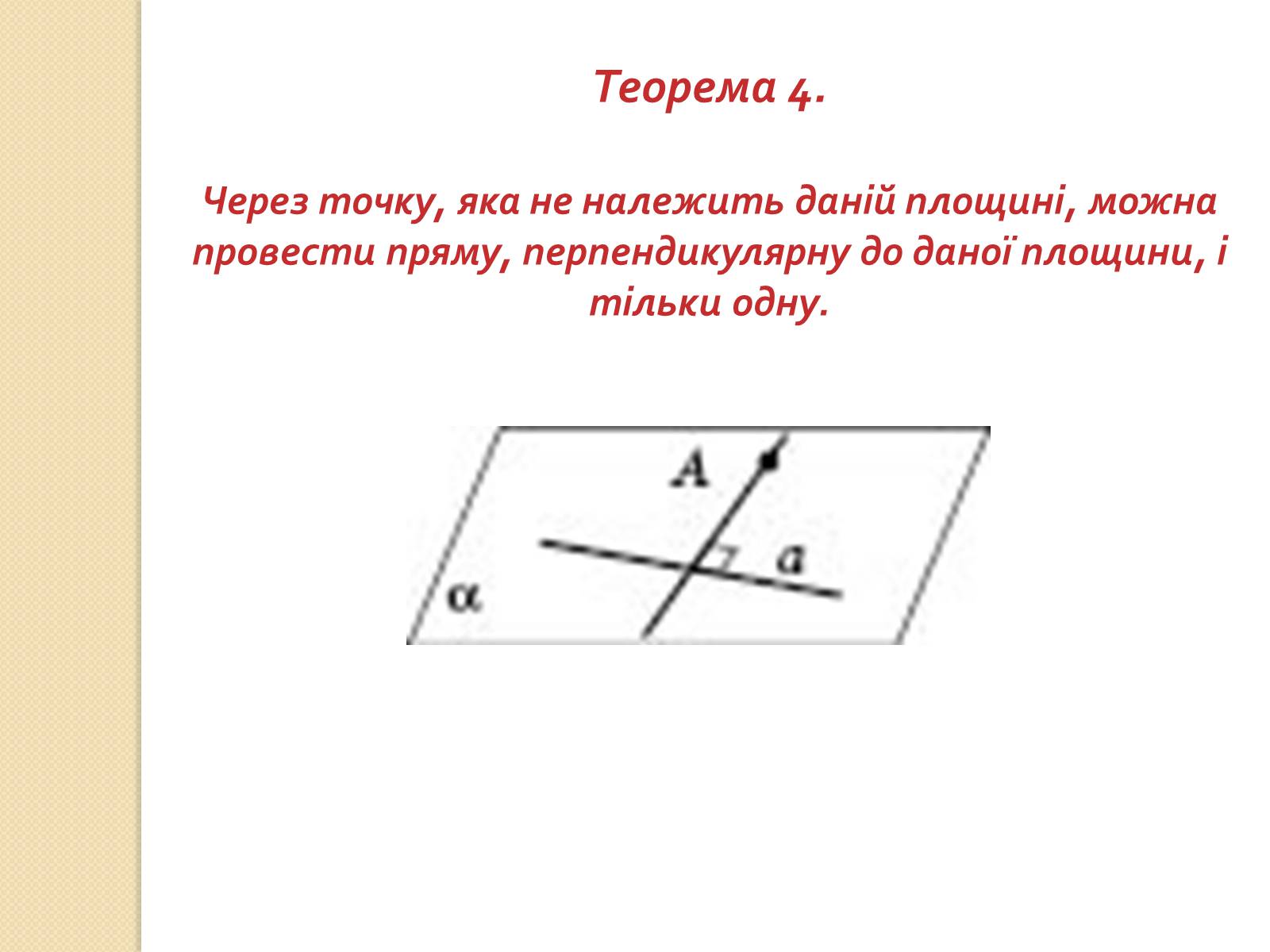
Теорема 4.
Через точку, яка не належить даній площині, можна провести пряму, перпендикулярну до даної площини, і тільки ­одну.

Теорема 5.
Якщо пряма перпендикулярна до однієї з двох паралельних прямих і лежить з ними в одній площині, то вона перпендикулярна і до другої прямої

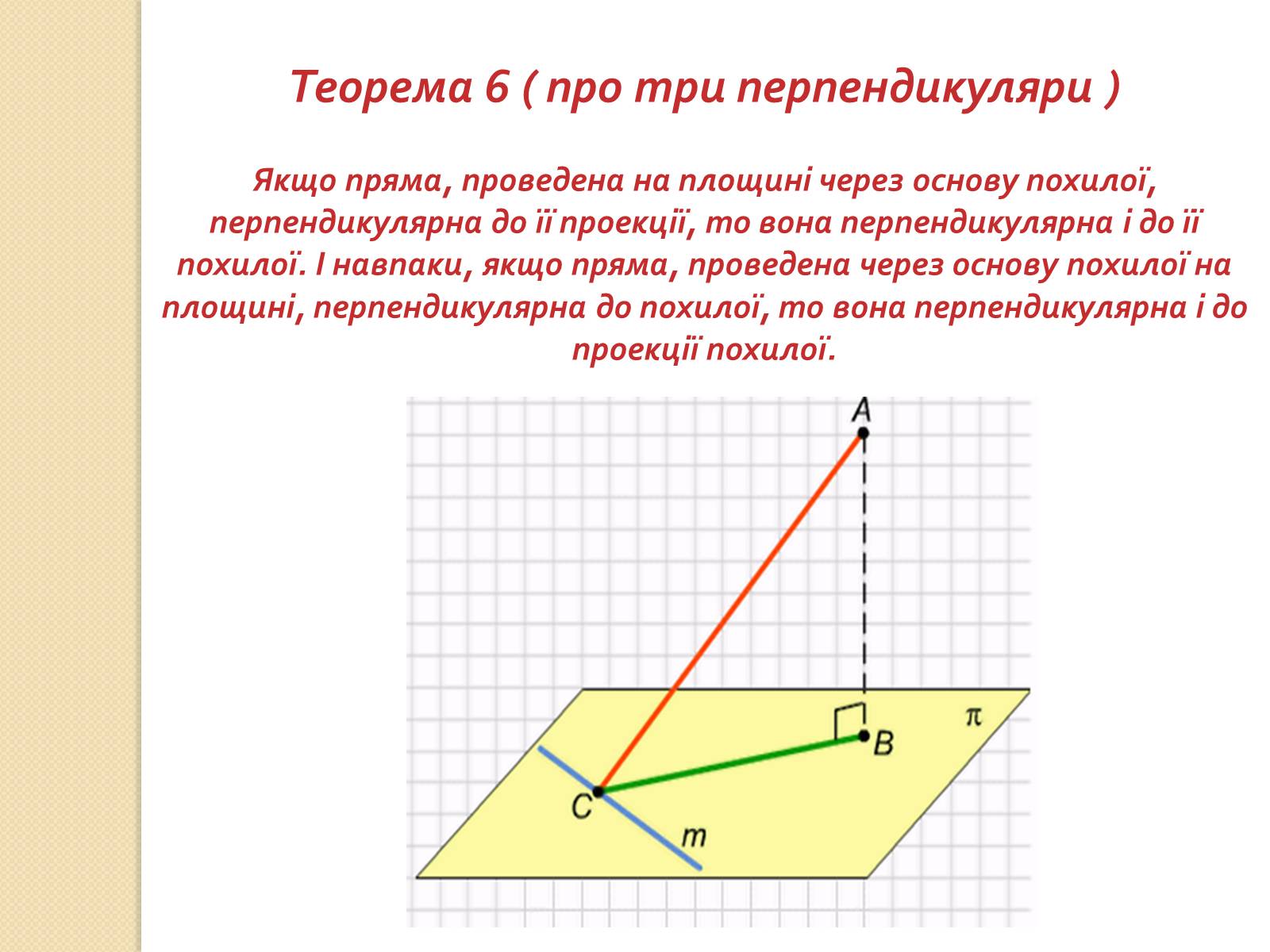
Теорема 6 ( про три перпендикуляри )
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до її похилої. І навпаки, якщо пряма, проведена через основу похилої на площині, перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.

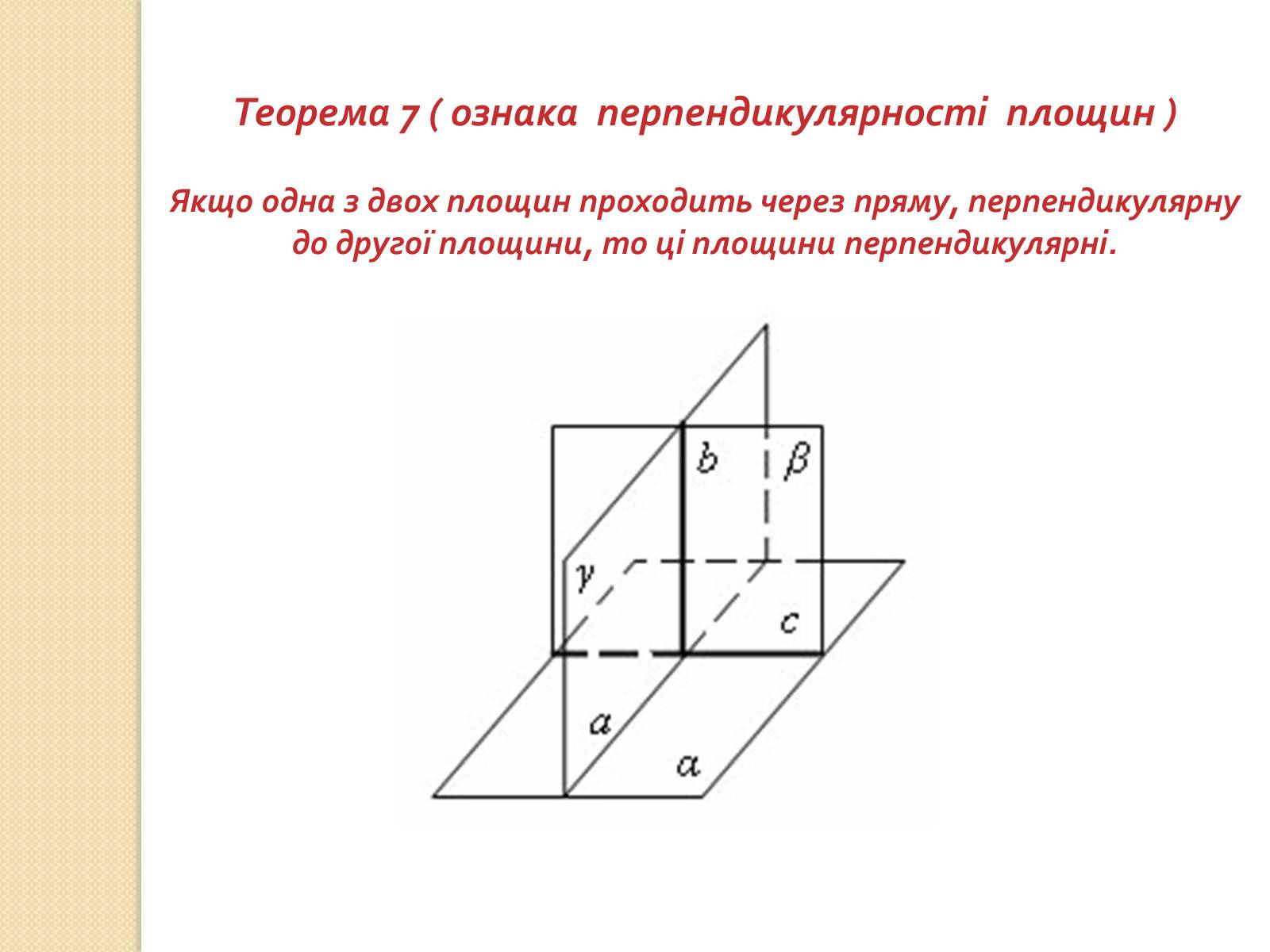
Теорема 7 ( ознака перпендикулярності площин )
Якщо одна з двох площин проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.

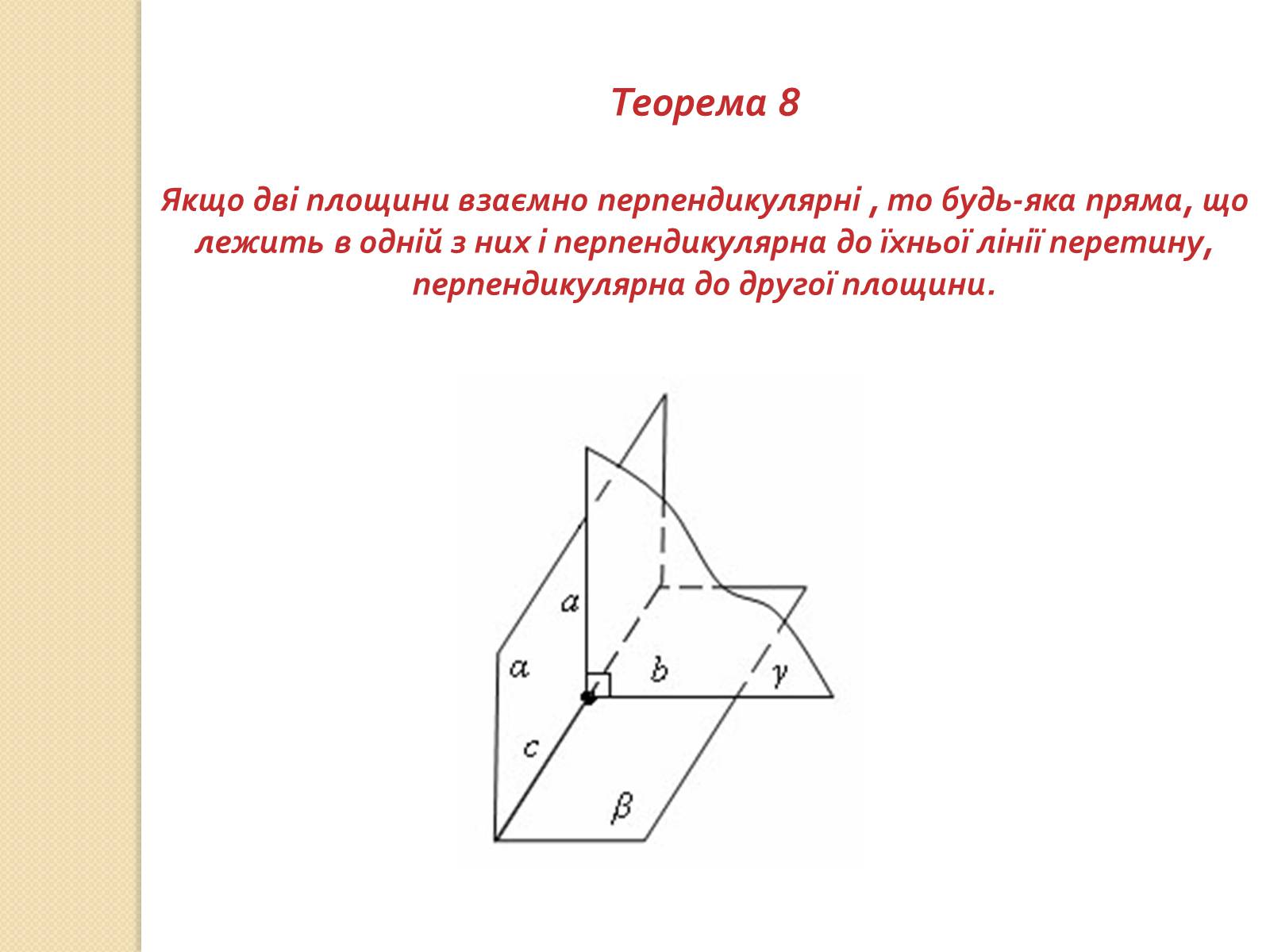
Теорема 8
Якщо дві площини взаємно перпендикулярні , то будь-яка пряма, що лежить в одній з них і перпендикулярна до їхньої лінії перетину, перпендикулярна до другої площини.

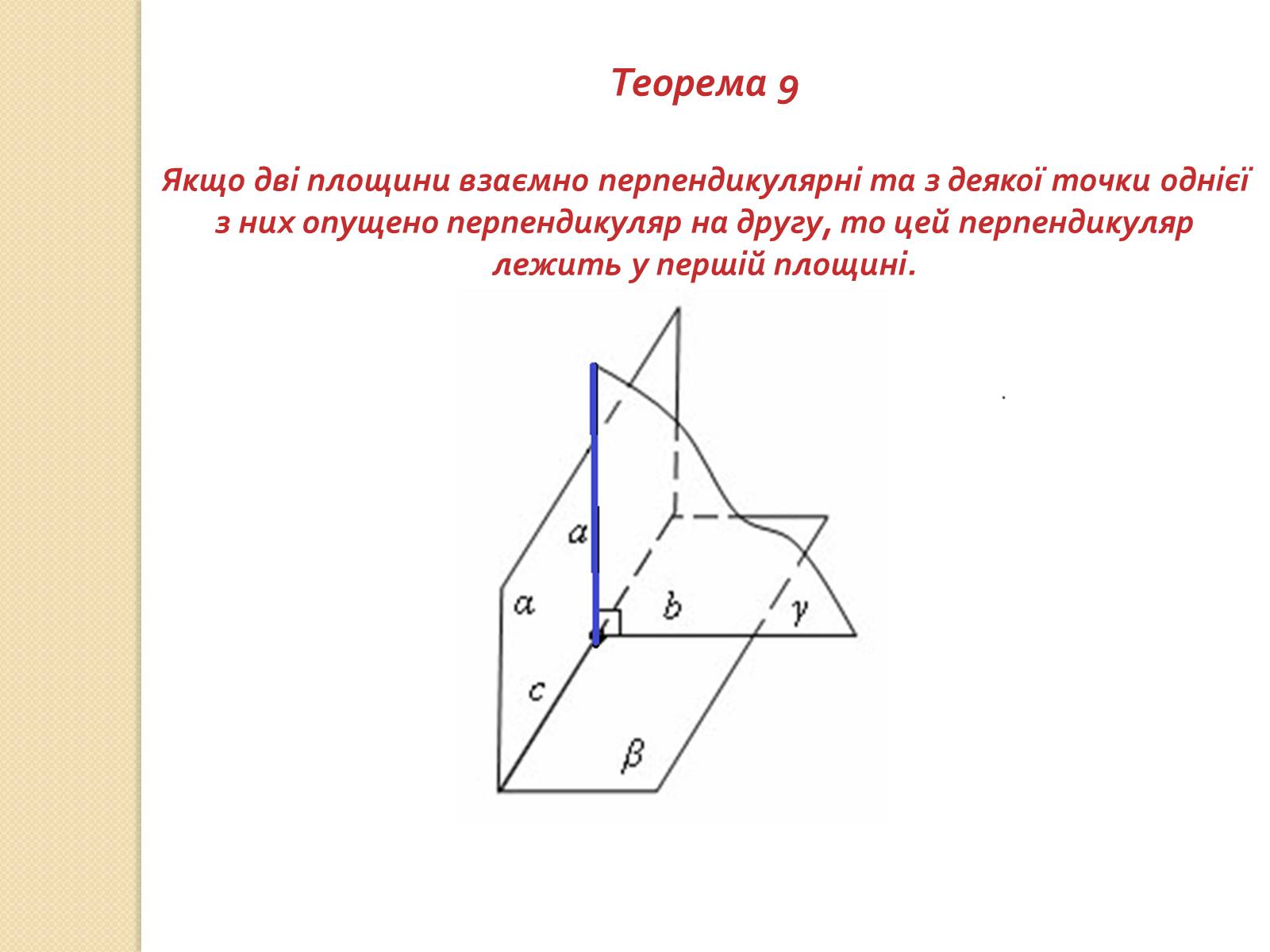
Теорема 9
Якщо дві площини взаємно перпендикулярні та з деякої точки однієї з них опущено перпендикуляр на другу, то цей перпендикуляр лежить у першій площині.

Вправа
У прямокутному паралелепіпеді ABCDA1B1C1D1 через відрізок DС1 і точку В проведено площину. Обчисліть периметр утвореного перерізу, якщо a,b,c – виміри паралелепіпеда, причому а=3см, b= 4 см, с= 6 см.

Кінець !