- Головна
- Готові шкільні презентації
- Презентація на тему «Тригонометричні функції»
Презентація на тему «Тригонометричні функції»
441
Слайд #1
Узагальнення по темі:«Тригонометричні функції»
Підготували:
Учні 10 класу
Колпакчі Яна
Федоренко Павло
Підготували:
Учні 10 класу
Колпакчі Яна
Федоренко Павло

Слайд #2
Вивчаючи матеріал цього параграфу ви дізналися:
Кутом в 1 радіан називають центральний кут кола,який спирається на дугу, довжина якого дорівнює радіусу кола;
Радіанна і градусна міра кута пов'язані формулами
Косинусом і синусом кута повороту називають відповідно абсцису x і ординату y точки P(x;y) одиничного кола,яку отримано з точки (1;0) у результаты повороту навколо початку координат на кут ;
Тангенсом кута повороту називають выдношення синусу кута до його косинуса:
Кутом в 1 радіан називають центральний кут кола,який спирається на дугу, довжина якого дорівнює радіусу кола;
Радіанна і градусна міра кута пов'язані формулами
Косинусом і синусом кута повороту називають відповідно абсцису x і ординату y точки P(x;y) одиничного кола,яку отримано з точки (1;0) у результаты повороту навколо початку координат на кут ;
Тангенсом кута повороту називають выдношення синусу кута до його косинуса:

Слайд #3
Котангенсом кута повороту називають відношення косинуса до синуса:
Значення синуса,косинуса,тангенса і котангенса кута залежно від того,кутом якої чверті є кут ,мають знаки які схематично зображені на рисунках:
Значення синуса,косинуса,тангенса і котангенса кута залежно від того,кутом якої чверті є кут ,мають знаки які схематично зображені на рисунках:

Слайд #4
Функція косинус є парною,а синус,тангес і котангес – непарними:
Функцією f називають періодичною,якщо існує таке число Т 0,що будь-якого х з області визначення функції f виконуються рівності f(х-Т)= f(х)= f(х+Т). Число Т називають періодом функції f.Якщо серед усіх періодів функції f існує додатний найменший період,то його називають головним періодом функції f;
Функцією f називають періодичною,якщо існує таке число Т 0,що будь-якого х з області визначення функції f виконуються рівності f(х-Т)= f(х)= f(х+Т). Число Т називають періодом функції f.Якщо серед усіх періодів функції f існує додатний найменший період,то його називають головним періодом функції f;

Слайд #5
Функції y=sinx і y=cosх є періодичними з головним періодом,рівним 2 ,а функція y=tgх і y=ctgх є періодичними з головним періодом рівним ;
Функції y=sinx , y=cosх , y=tgх , y=ctgх мають властивості,наведені в таблицях:
Властивості функції y=sinx
Область визначення
R
Область значень
Періодичність
Періодична з головним періодом,який дорівнює 2
Проміжки знакосталості
на кожному з проміжків виду
на кожному з проміжків
Функції y=sinx , y=cosх , y=tgх , y=ctgх мають властивості,наведені в таблицях:
Властивості функції y=sinx
Область визначення
R
Область значень
Періодичність
Періодична з головним періодом,який дорівнює 2
Проміжки знакосталості
на кожному з проміжків виду
на кожному з проміжків

Слайд #6
Парність
Непарна
Зростання/Спадання
Зростає на кожному з проміжків виду
Спадає на кожному з проміжків виду
Найбільше і найменше значення
Найбільшого значення,яке дорівнює 1,набуває в точках виду
Найменшого значення,яке дорівнює -1,набуває в точках виду
Непарна
Зростання/Спадання
Зростає на кожному з проміжків виду
Спадає на кожному з проміжків виду
Найбільше і найменше значення
Найбільшого значення,яке дорівнює 1,набуває в точках виду
Найменшого значення,яке дорівнює -1,набуває в точках виду

Слайд #7
Область визначення
R
Область значень
Періодичність
Періодична з головним періодом,який дорівнює 2
Проміжки знакосталості
на кожному з проміжків виду
на кожному з проміжків виду
Парність
Парна
Зростання/Спадання
Зростає на кожному з проміжків
Спадає на кожному з проміжків
Найбільше і найменше значення
Найбільше значення,яке дорівнює 1,набуває в точках виду
Найменше значення,яке дорівнює -1,набуває в точках виду
Власитивості функції y=cosx
R
Область значень
Періодичність
Періодична з головним періодом,який дорівнює 2
Проміжки знакосталості
на кожному з проміжків виду
на кожному з проміжків виду
Парність
Парна
Зростання/Спадання
Зростає на кожному з проміжків
Спадає на кожному з проміжків
Найбільше і найменше значення
Найбільше значення,яке дорівнює 1,набуває в точках виду
Найменше значення,яке дорівнює -1,набуває в точках виду
Власитивості функції y=cosx

Слайд #8
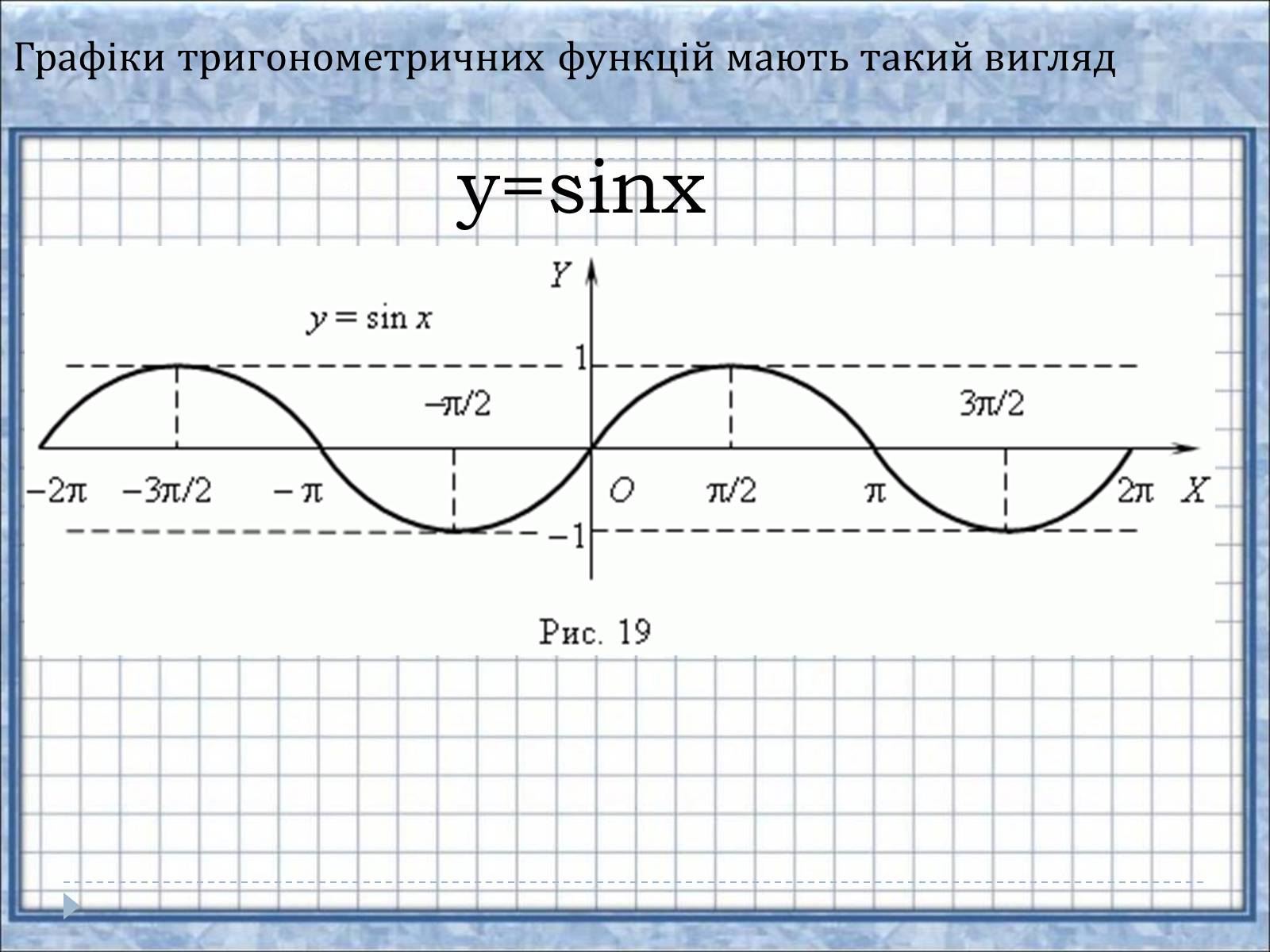
Графіки тригонометричних функцій мають такий вигляд
y=sinx
y=sinx
Слайд #9
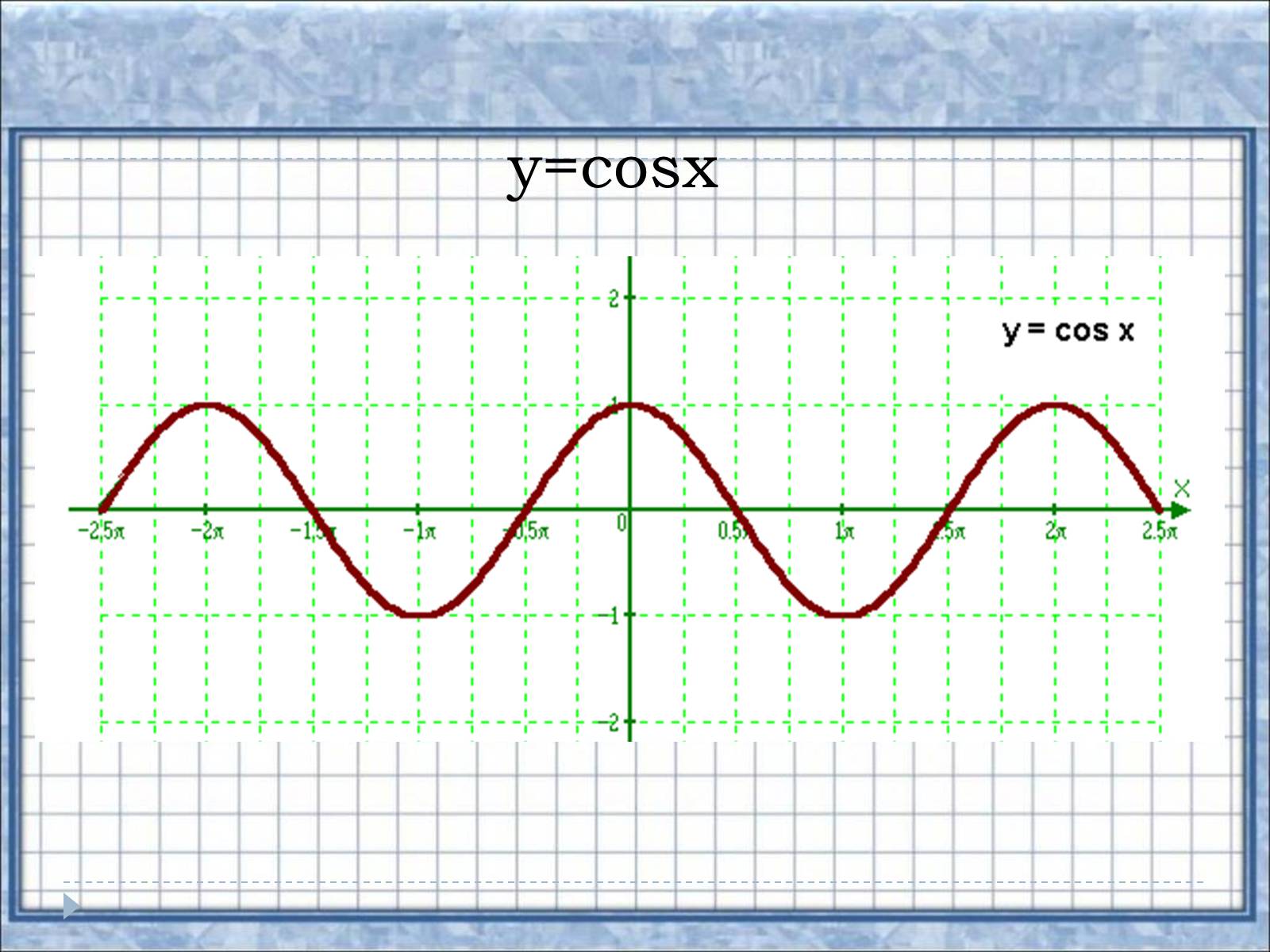
y=cosx
Слайд #10
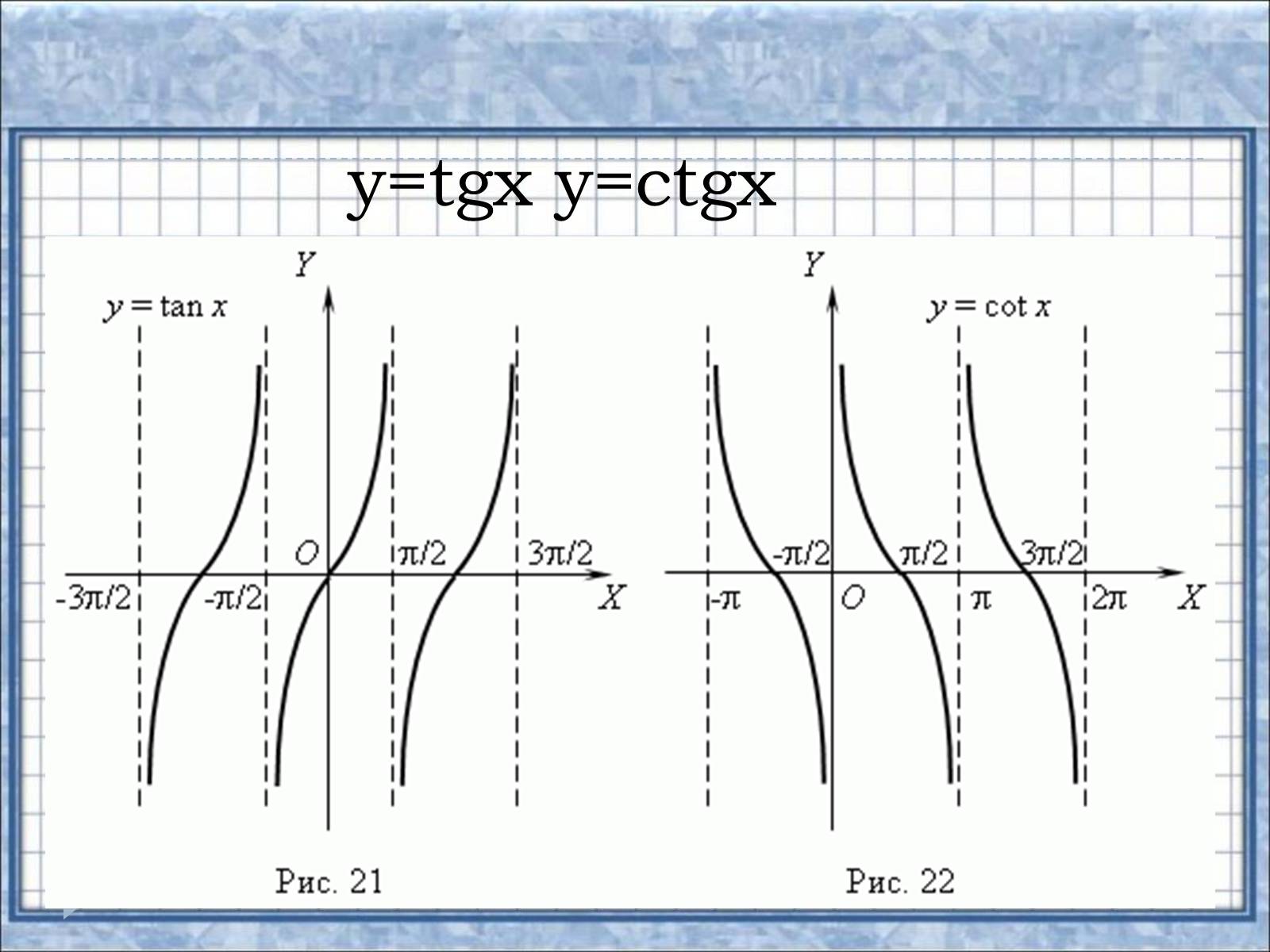
y=tgx y=ctgx
Слайд #11
Тригонометричні функції одного і того самого аргументу пов'язані формулами:

Слайд #12
Формули,які виражають через тригонометричні функції кутів і ,називають формулами додавання:

Слайд #13
Формули,які дозволяють зводити пошук значень тригонометричних функцій будь-якого кута до пошуку їх значень для кута від 0 до ,називають формулами зведення:

Слайд #14
Для того,щоб записати будь-яку з формул зведення,можна керуватися такими правилами:
У правій частині рівності ставлять той знак,який має ліва частина при
Якщо в лівій частині формули аргумент має вигляд
або ,то синус міняють на косинус,тангес на котангес і навпаки. Якщо аргумент має вигляд ,то зміни не відбувається
У правій частині рівності ставлять той знак,який має ліва частина при
Якщо в лівій частині формули аргумент має вигляд
або ,то синус міняють на косинус,тангес на котангес і навпаки. Якщо аргумент має вигляд ,то зміни не відбувається

Слайд #15
Формули,які виражають тригонометричні функції аргументу 2ἀ через тригонометричні функції аргументу ἀ,називають формули подвійного аргументу:

Слайд #16
Формули,які дозволяють знайти і , якщо відомо сos2ἀ,називать формулами понження степення:

Слайд #17
Суму або різницю тригонометричних функцій можна перетворити в добуток,використовуючи формули

Слайд #18
Добуток геометричних функцій можна перетворити в суму,використовуючи формули
