- Головна
- Готові шкільні презентації
- Презентація на тему «Об’єми і площі поверхонь геометричних тіл»
Презентація на тему «Об’єми і площі поверхонь геометричних тіл»
624
Слайд #1
Автор: Ананьєва Поліна
ГЕОМЕТРІЯ
11
Об'єми і площі поверхонь геометричних тіл
МІНІ-підручник
Об'єм та площа прямої призми і циліндра
Об'єм та площа піраміди
Об'єм та площа конуса
Об'єм та площа кулі
ГЕОМЕТРІЯ
11
Об'єми і площі поверхонь геометричних тіл
МІНІ-підручник
Об'єм та площа прямої призми і циліндра
Об'єм та площа піраміди
Об'єм та площа конуса
Об'єм та площа кулі

Слайд #2
Зміст
Поняття об'єму
Об'єм та площа
прямої призми і циліндра
Об'єм та площа
прямої піраміди і зрізаної піраміди
Об'єм та площа
прямої конуса і зрізного конуса
Об'єм та площа
прямої кулі і їїчастин
Поняття об'єму
Об'єм та площа
прямої призми і циліндра
Об'єм та площа
прямої піраміди і зрізаної піраміди
Об'єм та площа
прямої конуса і зрізного конуса
Об'єм та площа
прямої кулі і їїчастин

Слайд #3
Об'ємом геометричного тіла називається додатне число, яке характеризує частину простору, що займає геометричне тіло, і задовольняє таким умовам:
Слайд #4
Формула для об 'єму прямокутного паралелепіпеда
Теорема
Об'єм прямокутного паралелепіпеда
дорівнює добутку трьох його вимірів,
тобто якщо а, b, с — лінійні виміри
прямокутного паралелепіпеда, то
його об'єм V обчислюється за формулою
V = аbс .
Теорема
Об'єм прямокутного паралелепіпеда
дорівнює добутку трьох його вимірів,
тобто якщо а, b, с — лінійні виміри
прямокутного паралелепіпеда, то
його об'єм V обчислюється за формулою
V = аbс .

Слайд #5
Циліндром називається тіло, утворене обертанням прямокутника навколо його сторони.
Циліндр
Циліндр

Слайд #6
Призма – многогранник,
дві грані якого – рівні
n-кутники з
відповідно паралельними
сторонами, а всі інші
грані – паралелограми
Призма
дві грані якого – рівні
n-кутники з
відповідно паралельними
сторонами, а всі інші
грані – паралелограми
Призма

Слайд #7
Піраміда
P – вершина піраміди;
ABCD – основа піраміди;
∆PAB, ∆PBC, ∆PCD,
∆PDA – бічні грані;
PA, PB, PC, PD – бічні ребра;
AB, BC, CD, AD – ребра основи;
PO – висота, PO┴ABCD.
Піраміда – це многогранник, одна грань якого – довільний n-кутник, а всі інші – n граней трикутники, що мають спільну вершину.
P – вершина піраміди;
ABCD – основа піраміди;
∆PAB, ∆PBC, ∆PCD,
∆PDA – бічні грані;
PA, PB, PC, PD – бічні ребра;
AB, BC, CD, AD – ребра основи;
PO – висота, PO┴ABCD.
Піраміда – це многогранник, одна грань якого – довільний n-кутник, а всі інші – n граней трикутники, що мають спільну вершину.

Слайд #8
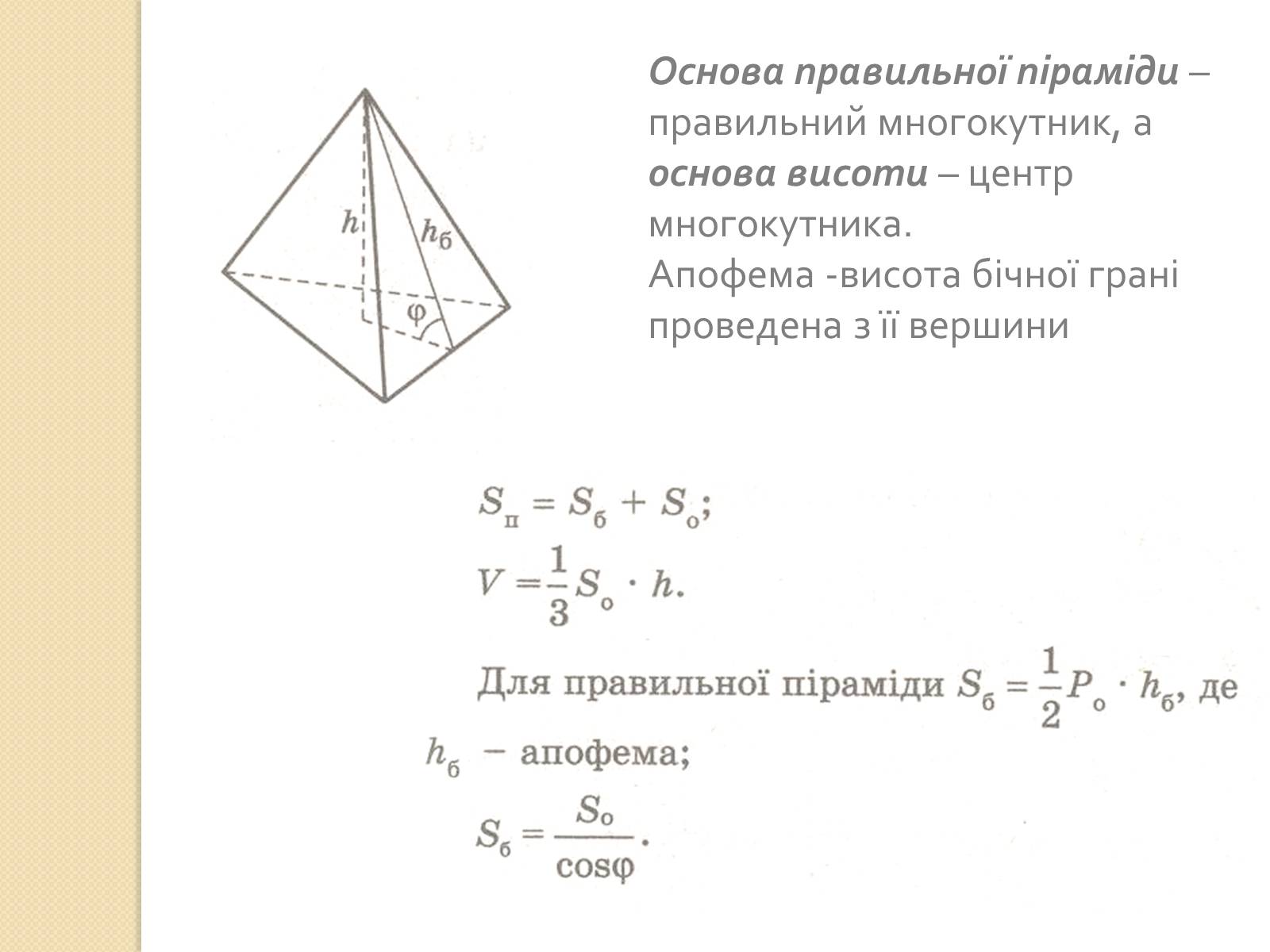
Основа правильної піраміди – правильний многокутник, а основа висоти – центр многокутника.
Апофема -висота бічної грані проведена з її вершини
Апофема -висота бічної грані проведена з її вершини
Слайд #9
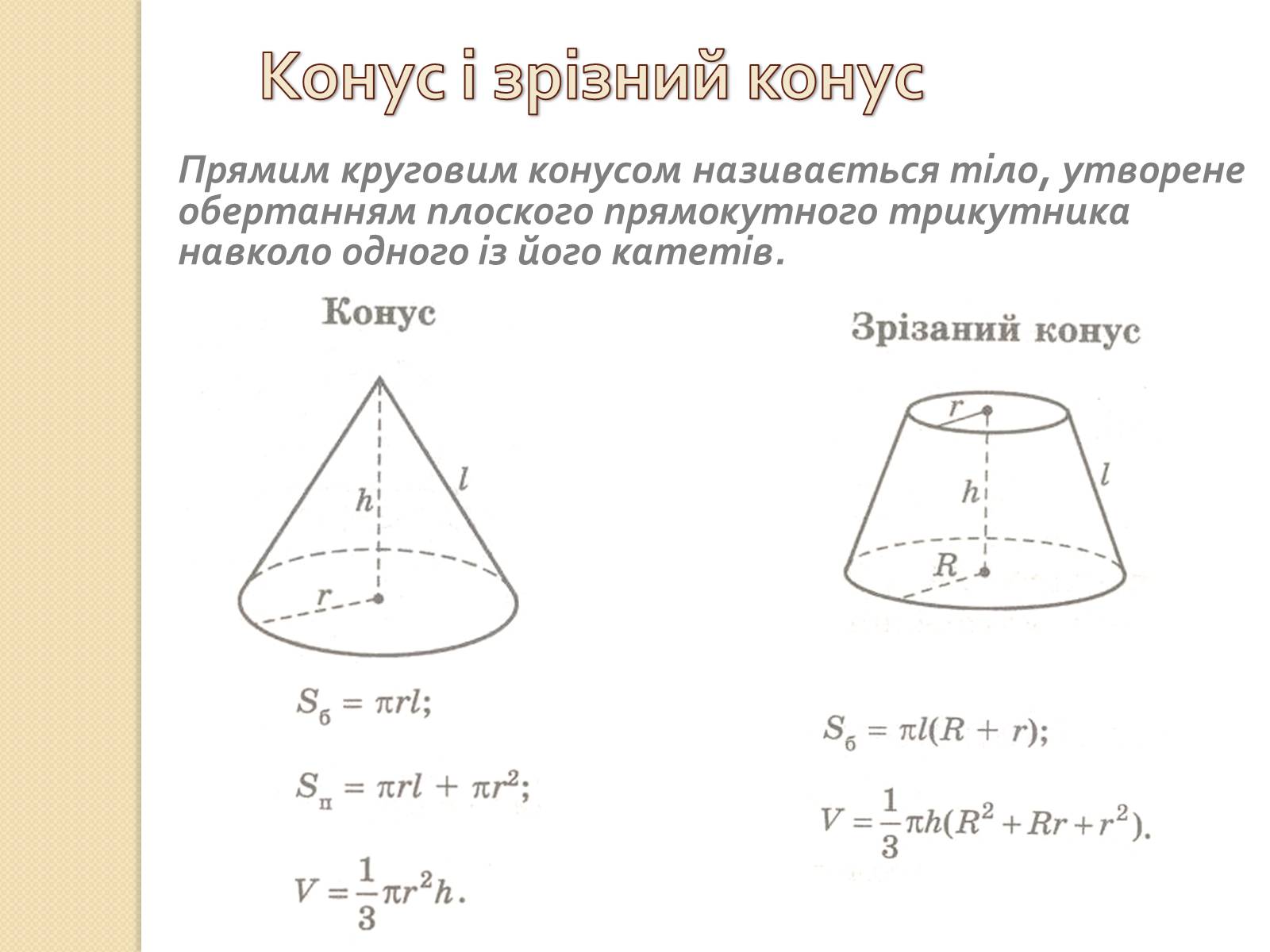
Конус і зрізний конус
Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів.
Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів.
Слайд #10
Куля і її частини
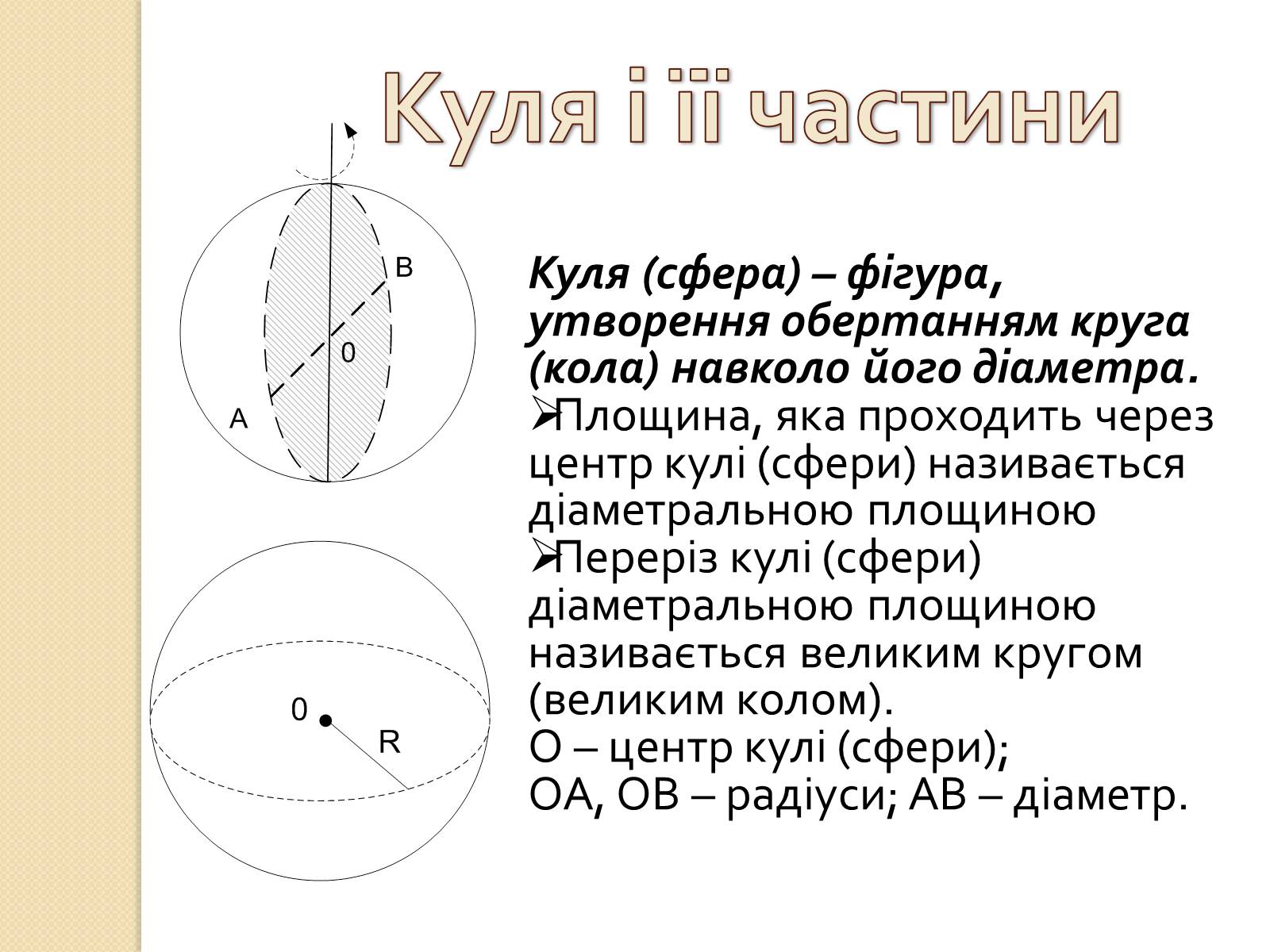
Куля (сфера) – фігура, утворення обертанням круга (кола) навколо його діаметра.
Площина, яка проходить через центр кулі (сфери) називається діаметральною площиною
Переріз кулі (сфери) діаметральною площиною називається великим кругом (великим колом).
О – центр кулі (сфери);
ОА, ОВ – радіуси; АВ – діаметр.
Куля (сфера) – фігура, утворення обертанням круга (кола) навколо його діаметра.
Площина, яка проходить через центр кулі (сфери) називається діаметральною площиною
Переріз кулі (сфери) діаметральною площиною називається великим кругом (великим колом).
О – центр кулі (сфери);
ОА, ОВ – радіуси; АВ – діаметр.
Слайд #11
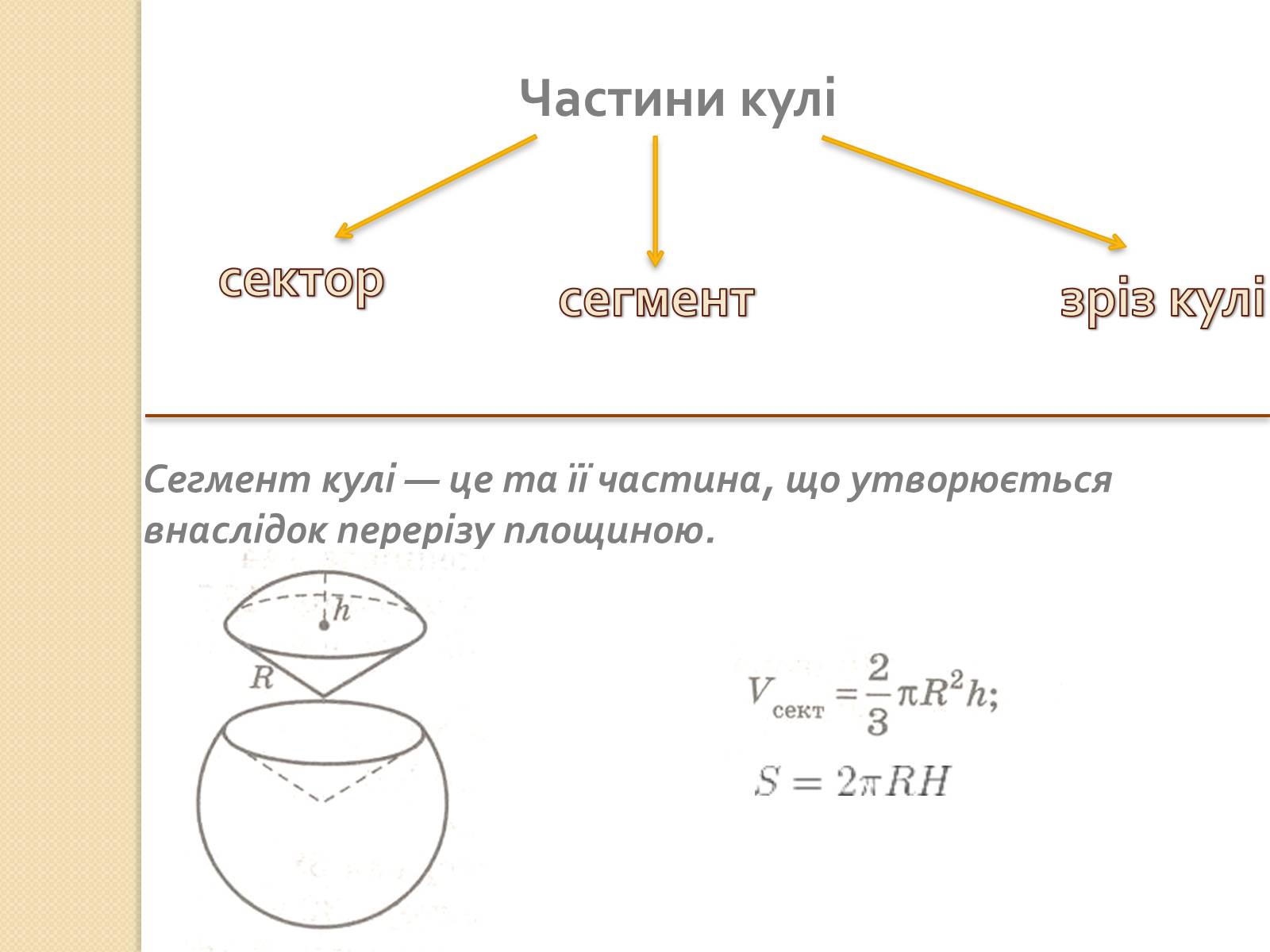
Частини кулі
Сегмент кулі — це та її частина, що утворюється внаслідок перерізу площиною.
сектор
сегмент
зріз кулі
Сегмент кулі — це та її частина, що утворюється внаслідок перерізу площиною.
сектор
сегмент
зріз кулі
Слайд #12
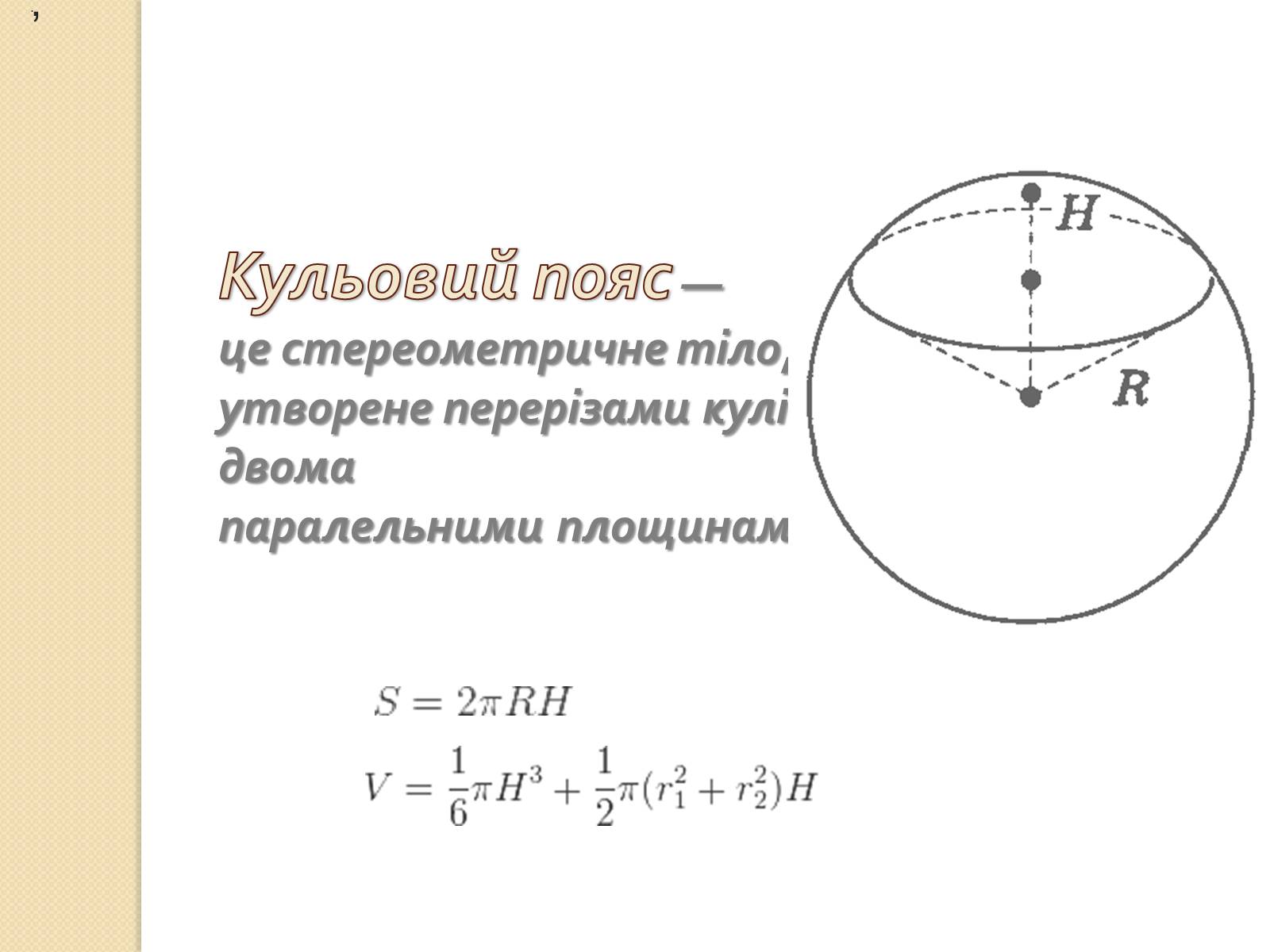
Кульовий пояс — це стереометричне тіло, утворене перерізами кулі двома паралельними площинами
,
.
,
.
Слайд #13
Сектор складається з кульового сегмента та конуса, основа якого збігається з основою сегмента, а вершина — з центром кулі.
.
S=
.
S=

Слайд #14
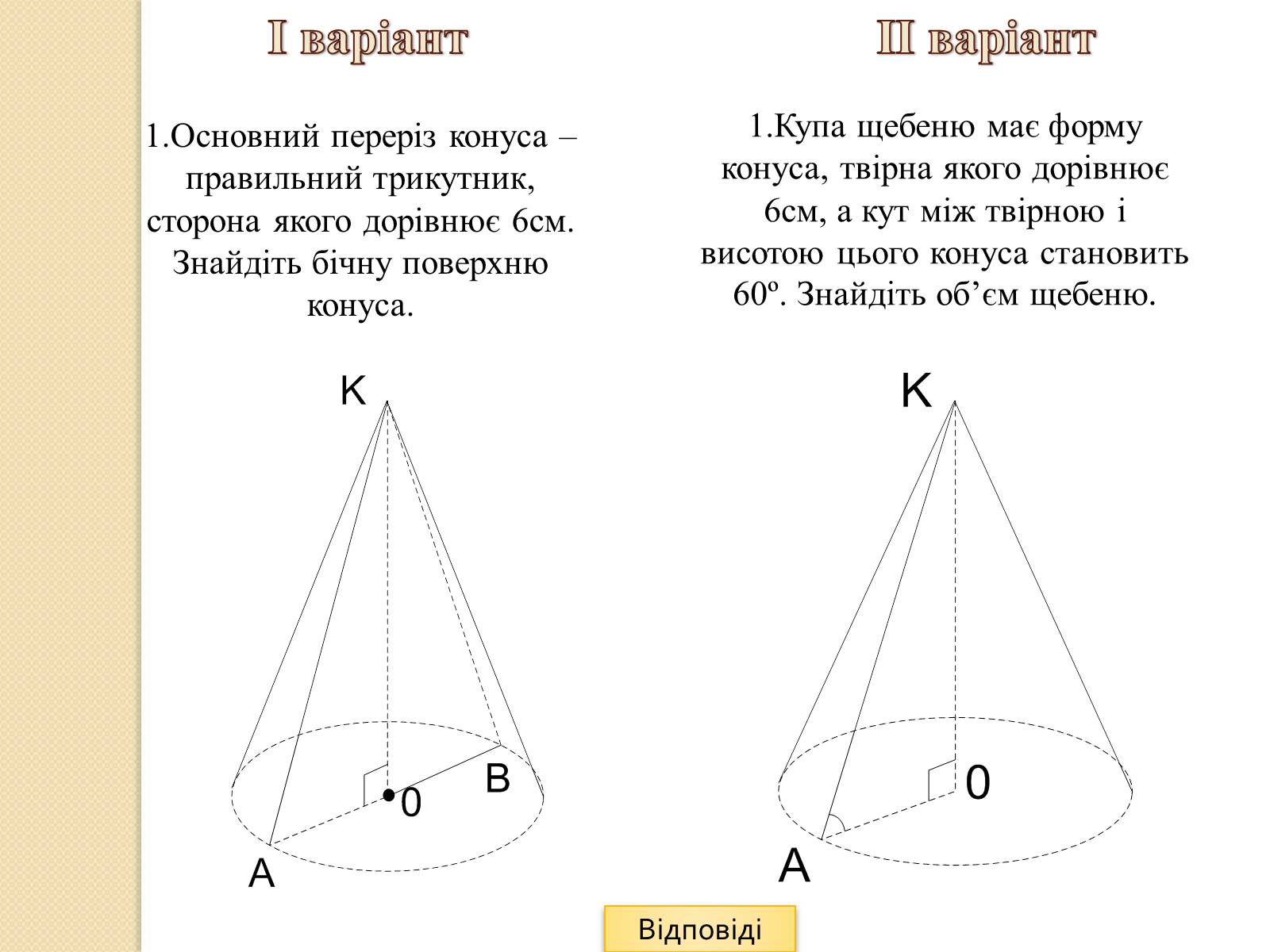
1.Основний переріз конуса – правильний трикутник, сторона якого дорівнює 6см. Знайдіть бічну поверхню конуса.
1.Купа щебеню має форму конуса, твірна якого дорівнює 6см, а кут між твірною і висотою цього конуса становить 60º. Знайдіть об'єм щебеню.
Відповіді
І варіант ІІ варіант
1.Купа щебеню має форму конуса, твірна якого дорівнює 6см, а кут між твірною і висотою цього конуса становить 60º. Знайдіть об'єм щебеню.
Відповіді
І варіант ІІ варіант
Слайд #15
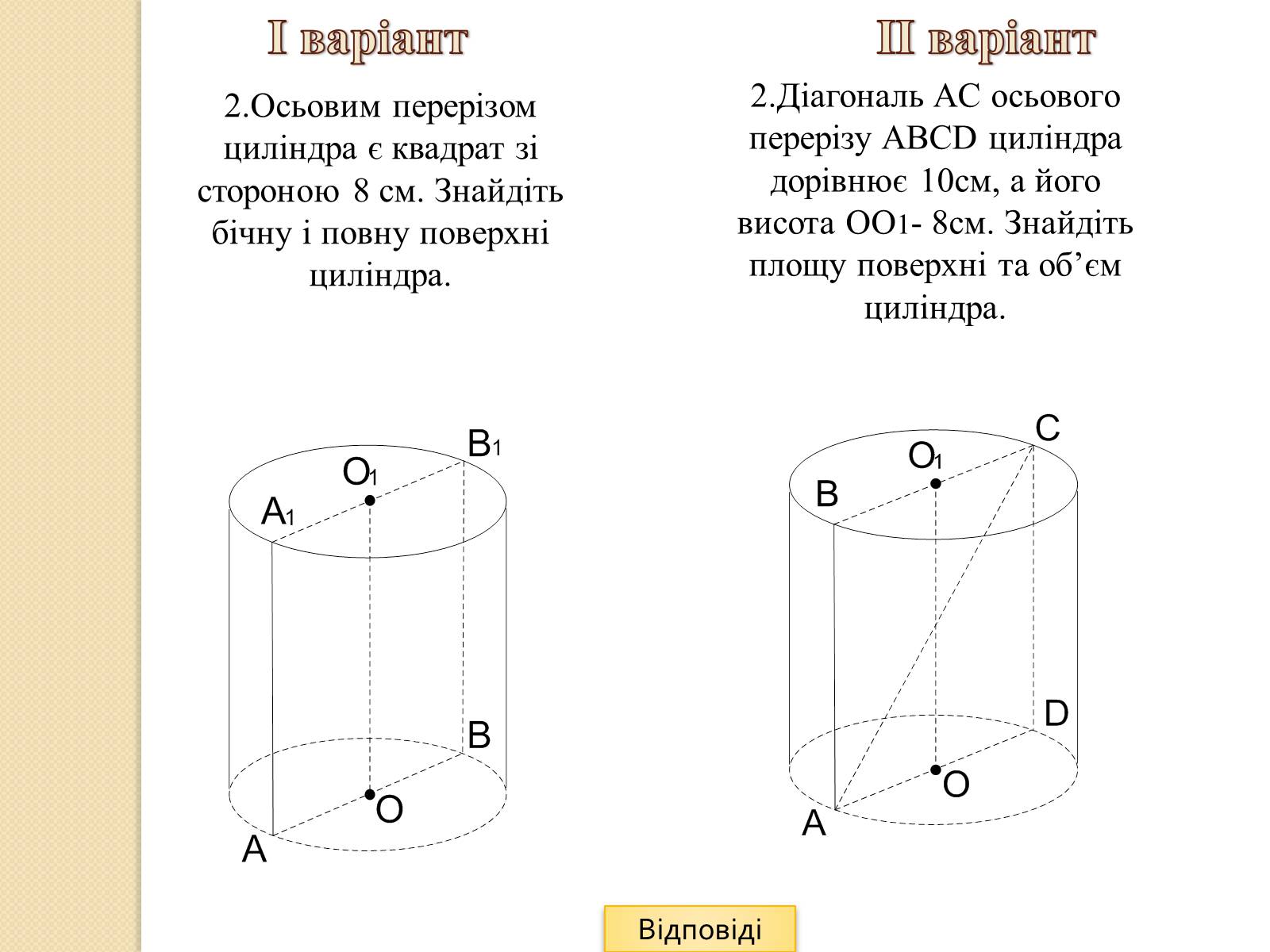
2.Діагональ AC осьового перерізу ABCD циліндра дорівнює 10см, а його висота ОО1- 8см. Знайдіть площу поверхні та об'єм циліндра.
2.Осьовим перерізом циліндра є квадрат зі стороною 8 см. Знайдіть бічну і повну поверхні циліндра.
Відповіді
І варіант ІІ варіант
2.Осьовим перерізом циліндра є квадрат зі стороною 8 см. Знайдіть бічну і повну поверхні циліндра.
Відповіді
І варіант ІІ варіант
Слайд #16
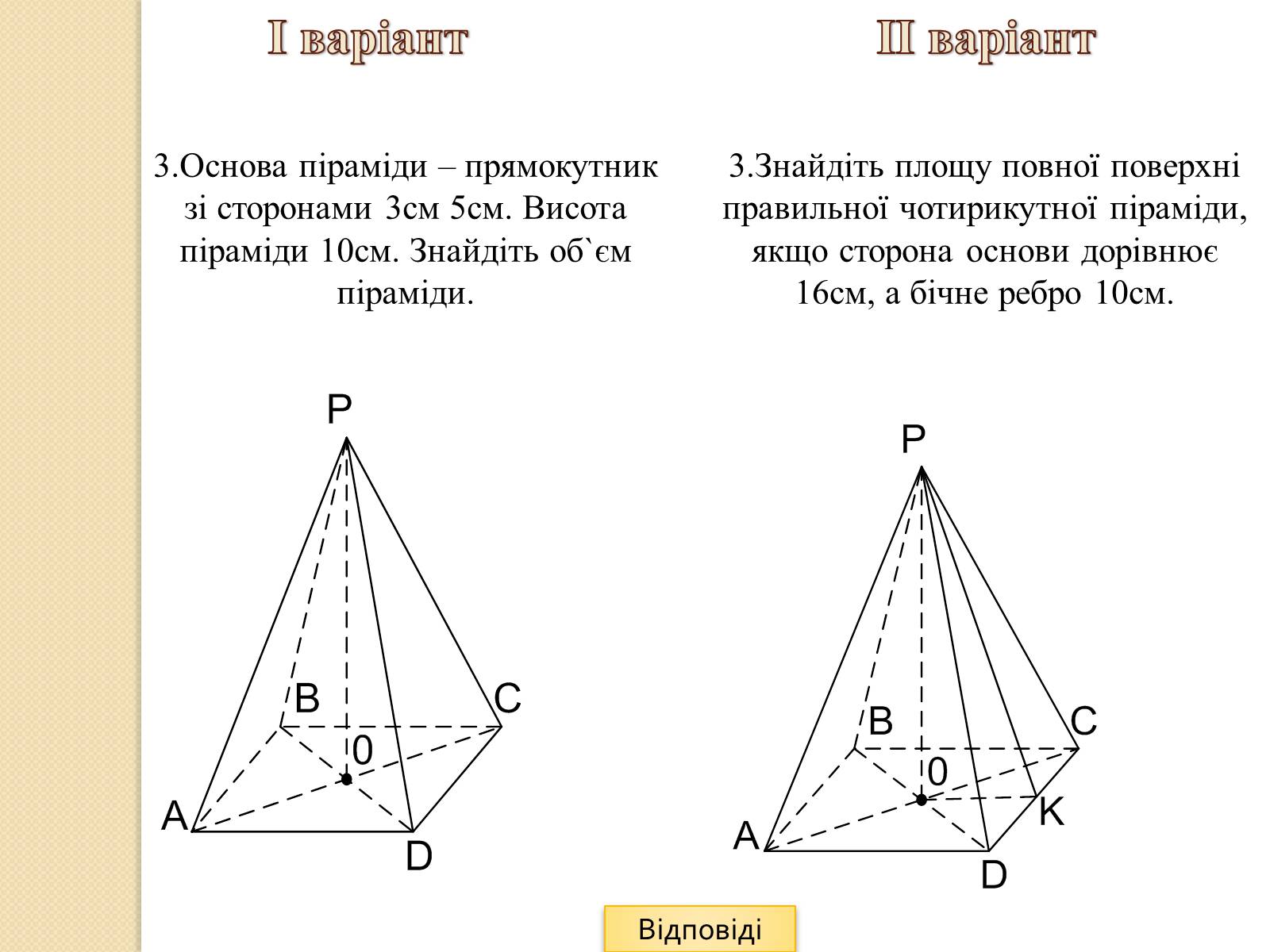
3.Основа піраміди – прямокутник зі сторонами 3см 5см. Висота піраміди 10см. Знайдіть об`єм піраміди.
3.Знайдіть площу повної поверхні правильної чотирикутної піраміди, якщо сторона основи дорівнює 16см, а бічне ребро 10см.
Відповіді
І варіант ІІ варіант
3.Знайдіть площу повної поверхні правильної чотирикутної піраміди, якщо сторона основи дорівнює 16см, а бічне ребро 10см.
Відповіді
І варіант ІІ варіант
Слайд #17
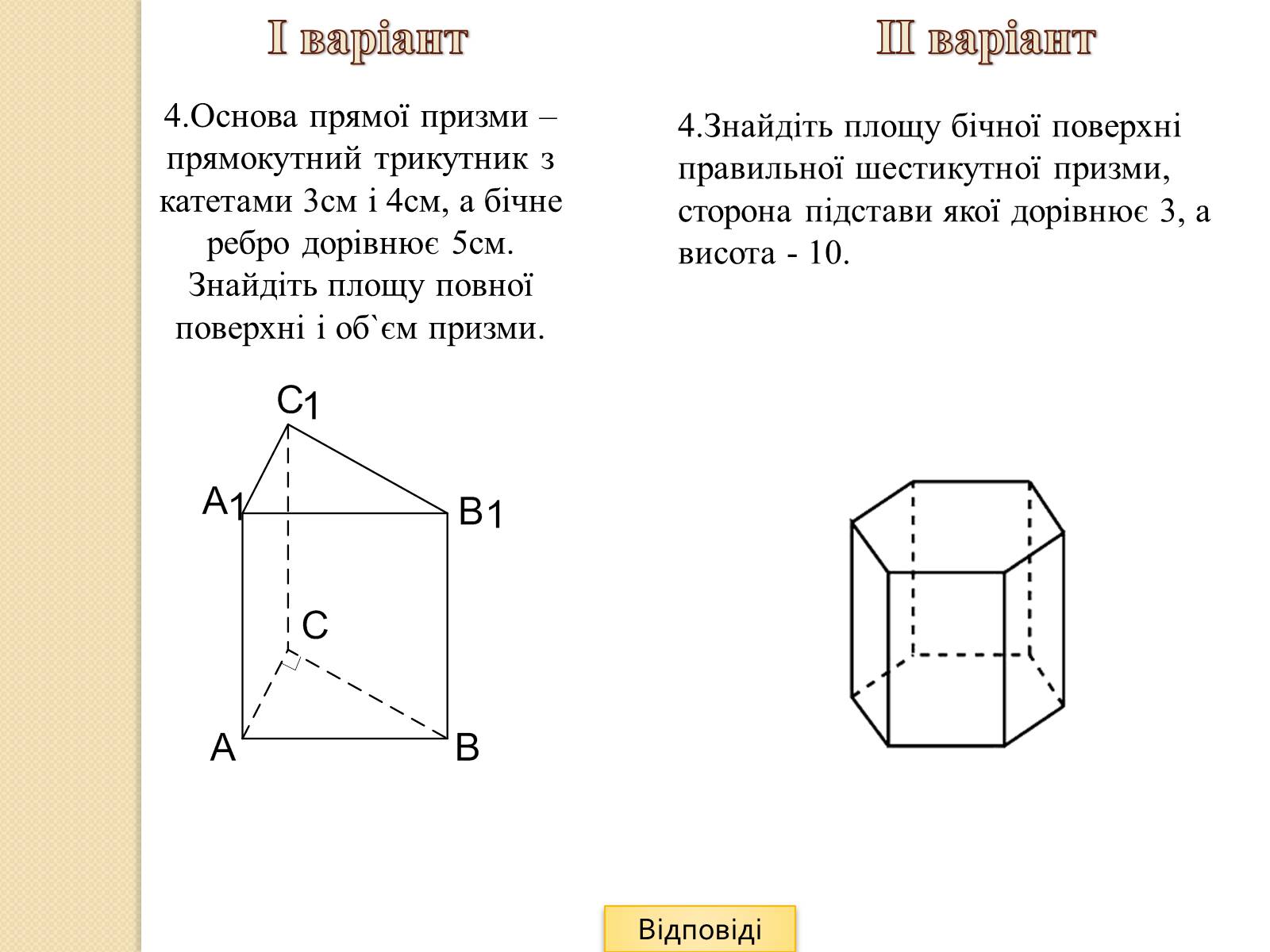
4.Основа прямої призми – прямокутний трикутник з катетами 3см і 4см, а бічне ребро дорівнює 5см. Знайдіть площу повної поверхні і об`єм призми.
4.Знайдіть площу бічної поверхні правильної шестикутної призми, сторона підстави якої дорівнює 3, а висота - 10.
Відповіді
І варіант ІІ варіант
4.Знайдіть площу бічної поверхні правильної шестикутної призми, сторона підстави якої дорівнює 3, а висота - 10.
Відповіді
І варіант ІІ варіант
Слайд #18
Дано: конус, ΔАКВ – правильний АК=КВ=АВ=6см.
Знайти: Sбічн.
Розв'язання
Sбічн.=πRL; L=KB=6см.
ΔАКВ – правильний, то КО – висота і медіана АО=ОВ=3см, R=3см.
Sбічн.=πRL=π*3*6=18π (см²)
Відповідь: 18π см²
Дано: конус, АК – твірна,
АО – висота.
ےАКО=60º, АК=6см.
Знайти: Vкон.
Розв'язання
V=1/3 πR²H
ΔАКО – прямокутний, ےАКО=60º, то ےКАО=30º.
КО=1/2*6=3(см) (катет, що лежить проти кута 30º)
За теоремою Піфагора з ΔАКО КО=√АК² – АО²=√6²-3²=√27=3√3
V=1/3πR²H=1/3π*(3√3)²*3=27π(см³)
Відповідь: 27π см³
До завдань
Знайти: Sбічн.
Розв'язання
Sбічн.=πRL; L=KB=6см.
ΔАКВ – правильний, то КО – висота і медіана АО=ОВ=3см, R=3см.
Sбічн.=πRL=π*3*6=18π (см²)
Відповідь: 18π см²
Дано: конус, АК – твірна,
АО – висота.
ےАКО=60º, АК=6см.
Знайти: Vкон.
Розв'язання
V=1/3 πR²H
ΔАКО – прямокутний, ےАКО=60º, то ےКАО=30º.
КО=1/2*6=3(см) (катет, що лежить проти кута 30º)
За теоремою Піфагора з ΔАКО КО=√АК² – АО²=√6²-3²=√27=3√3
V=1/3πR²H=1/3π*(3√3)²*3=27π(см³)
Відповідь: 27π см³
До завдань

Слайд #19
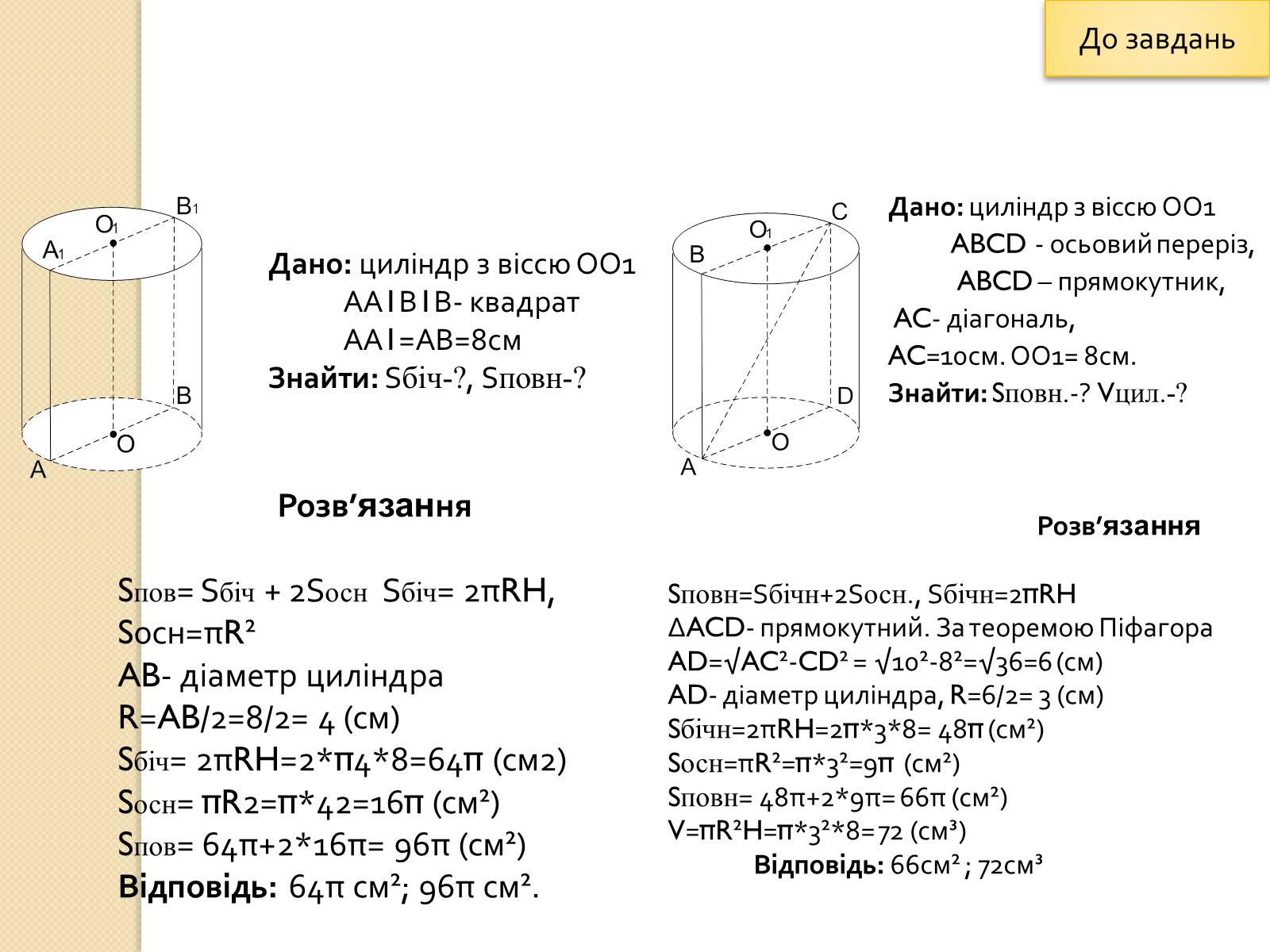
Дано: циліндр з віссю ОО1
АА1В1В- квадрат
АА1=АВ=8см
Знайти: Sбіч-?, Sповн-?
Розв'язання
Sпов= Sбіч + 2Sосн Sбіч= 2πRH, Sосн=πR²
AB- діаметр циліндра R=AB/2=8/2= 4 (см)
Sбіч= 2πRH=2*π4*8=64π (см2)
Sосн= πR2=π*42=16π (см²)
Sпов= 64π+2*16π= 96π (см²)
Відповідь: 64π см²; 96π см².
Дано: циліндр з віссю ОО1
ABCD - осьовий переріз,
ABCD – прямокутник,
AC- діагональ,
AC=10см. ОО1= 8см.
Знайти: Sповн.-? Vцил.-?
Розв'язання
Sповн=Sбічн+2Sосн., Sбічн=2πRH
∆ACD- прямокутний. За теоремою Піфагора
AD=√AC²-CD² = √10²-8²=√36=6 (см)
AD- діаметр циліндра, R=6/2= 3 (см)
Sбічн=2πRH=2π*3*8= 48π (см²)
Sосн=πR²=π*3²=9π (см²)
Sповн= 48π+2*9π= 66π (см²)
V=πR²H=π*3²*8= 72 (см³)
Відповідь: 66см² ; 72см³
До завдань
АА1В1В- квадрат
АА1=АВ=8см
Знайти: Sбіч-?, Sповн-?
Розв'язання
Sпов= Sбіч + 2Sосн Sбіч= 2πRH, Sосн=πR²
AB- діаметр циліндра R=AB/2=8/2= 4 (см)
Sбіч= 2πRH=2*π4*8=64π (см2)
Sосн= πR2=π*42=16π (см²)
Sпов= 64π+2*16π= 96π (см²)
Відповідь: 64π см²; 96π см².
Дано: циліндр з віссю ОО1
ABCD - осьовий переріз,
ABCD – прямокутник,
AC- діагональ,
AC=10см. ОО1= 8см.
Знайти: Sповн.-? Vцил.-?
Розв'язання
Sповн=Sбічн+2Sосн., Sбічн=2πRH
∆ACD- прямокутний. За теоремою Піфагора
AD=√AC²-CD² = √10²-8²=√36=6 (см)
AD- діаметр циліндра, R=6/2= 3 (см)
Sбічн=2πRH=2π*3*8= 48π (см²)
Sосн=πR²=π*3²=9π (см²)
Sповн= 48π+2*9π= 66π (см²)
V=πR²H=π*3²*8= 72 (см³)
Відповідь: 66см² ; 72см³
До завдань
Слайд #20
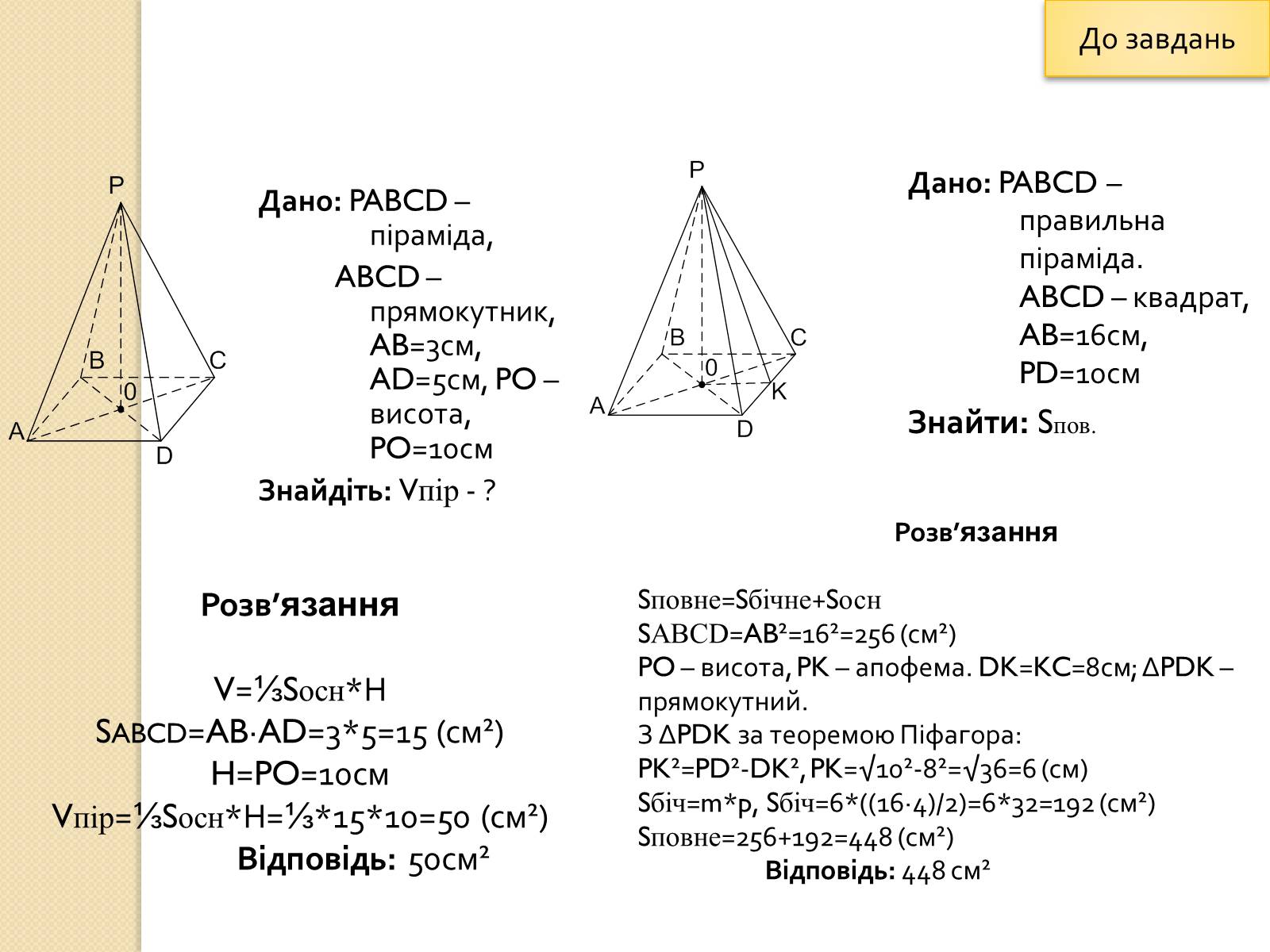
Дано: PABCD – піраміда,
ABCD – прямокутник, AB=3см, AD=5см, PO – висота, PO=10см
Знайдіть: Vпір - ?
Розв'язання
V=⅓Sосн*Н
SABCD=AB∙AD=3*5=15 (см²)
H=PO=10см
Vпір=⅓Sосн*Н=⅓*15*10=50 (см²)
Відповідь: 50см²
Дано: PABCD – правильна піраміда. ABCD – квадрат, AB=16см, PD=10см
Знайти: Sпов.
Розв'язання
Sповне=Sбічне+Sосн
SABCD=AB²=16²=256 (см²)
PO – висота, PK – апофема. DK=KC=8см; ∆PDK – прямокутний.
З ∆PDK за теоремою Піфагора:
PK²=PD²-DK², PK=√10²-8²=√36=6 (см)
Sбіч=m*p, Sбіч=6*((16∙4)/2)=6*32=192 (см²)
Sповне=256+192=448 (см²)
Відповідь: 448 см²
До завдань
ABCD – прямокутник, AB=3см, AD=5см, PO – висота, PO=10см
Знайдіть: Vпір - ?
Розв'язання
V=⅓Sосн*Н
SABCD=AB∙AD=3*5=15 (см²)
H=PO=10см
Vпір=⅓Sосн*Н=⅓*15*10=50 (см²)
Відповідь: 50см²
Дано: PABCD – правильна піраміда. ABCD – квадрат, AB=16см, PD=10см
Знайти: Sпов.
Розв'язання
Sповне=Sбічне+Sосн
SABCD=AB²=16²=256 (см²)
PO – висота, PK – апофема. DK=KC=8см; ∆PDK – прямокутний.
З ∆PDK за теоремою Піфагора:
PK²=PD²-DK², PK=√10²-8²=√36=6 (см)
Sбіч=m*p, Sбіч=6*((16∙4)/2)=6*32=192 (см²)
Sповне=256+192=448 (см²)
Відповідь: 448 см²
До завдань
Слайд #21
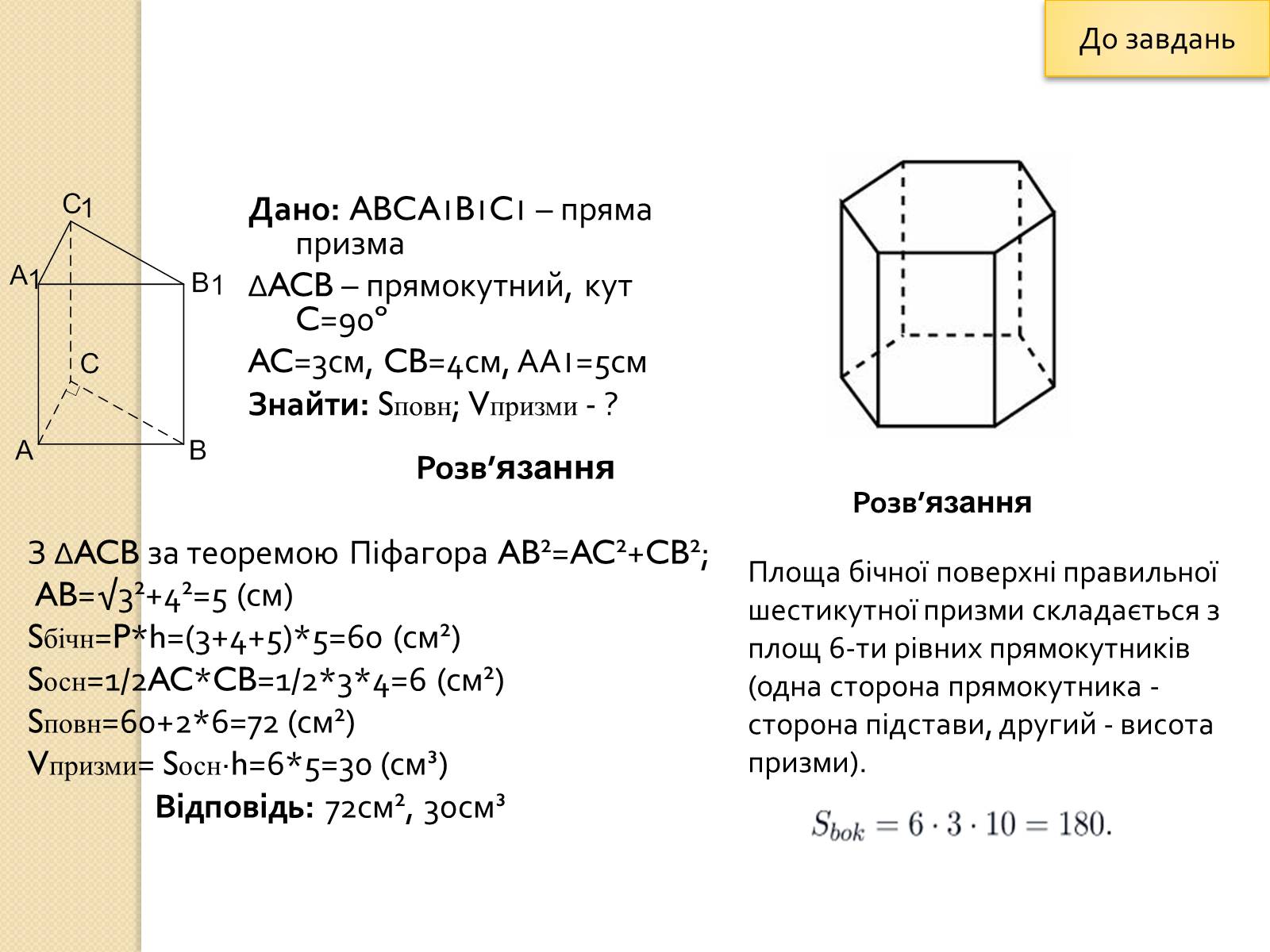
Дано: ABCA1B1C1 – пряма призма
∆ACB – прямокутний, кут C=90º
AC=3см, CB=4см, АА1=5см
Знайти: Sповн; Vпризми - ?
Розв'язання
З ∆ACB за теоремою Піфагора AB²=AC²+CB²;
AB=√3²+4²=5 (см)
Sбічн=P*h=(3+4+5)*5=60 (см²)
Sосн=1/2AC*CB=1/2*3*4=6 (см²)
Sповн=60+2*6=72 (см²)
Vпризми= Sосн∙h=6*5=30 (см³)
Відповідь: 72см², 30см³
Розв'язання
Площа бічної поверхні правильної шестикутної призми складається з площ 6-ти рівних прямокутників (одна сторона прямокутника - сторона підстави, другий - висота призми).
До завдань
∆ACB – прямокутний, кут C=90º
AC=3см, CB=4см, АА1=5см
Знайти: Sповн; Vпризми - ?
Розв'язання
З ∆ACB за теоремою Піфагора AB²=AC²+CB²;
AB=√3²+4²=5 (см)
Sбічн=P*h=(3+4+5)*5=60 (см²)
Sосн=1/2AC*CB=1/2*3*4=6 (см²)
Sповн=60+2*6=72 (см²)
Vпризми= Sосн∙h=6*5=30 (см³)
Відповідь: 72см², 30см³
Розв'язання
Площа бічної поверхні правильної шестикутної призми складається з площ 6-ти рівних прямокутників (одна сторона прямокутника - сторона підстави, другий - висота призми).
До завдань