- Головна
- Готові шкільні презентації
- Презентація на тему «Піраміда» (варіант 4)
Презентація на тему «Піраміда» (варіант 4)
256
Слайд #1
ПІРАМІДИ
Підготувала Островерх Ольга, 11-Б клас
Підготувала Островерх Ольга, 11-Б клас

Слайд #2
Піраміда — багатогранник, який складається з плоского багатокутника і точки (яка не лежить у площині основи) та всіх відрізків, що сполучають вершину піраміди з точками основи.
Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами.
Неправильна шестигранна
піраміда
Відрізки, що сполучають вершину піраміди з вершинами основи, називаються бічними ребрами.
Неправильна шестигранна
піраміда

Слайд #3
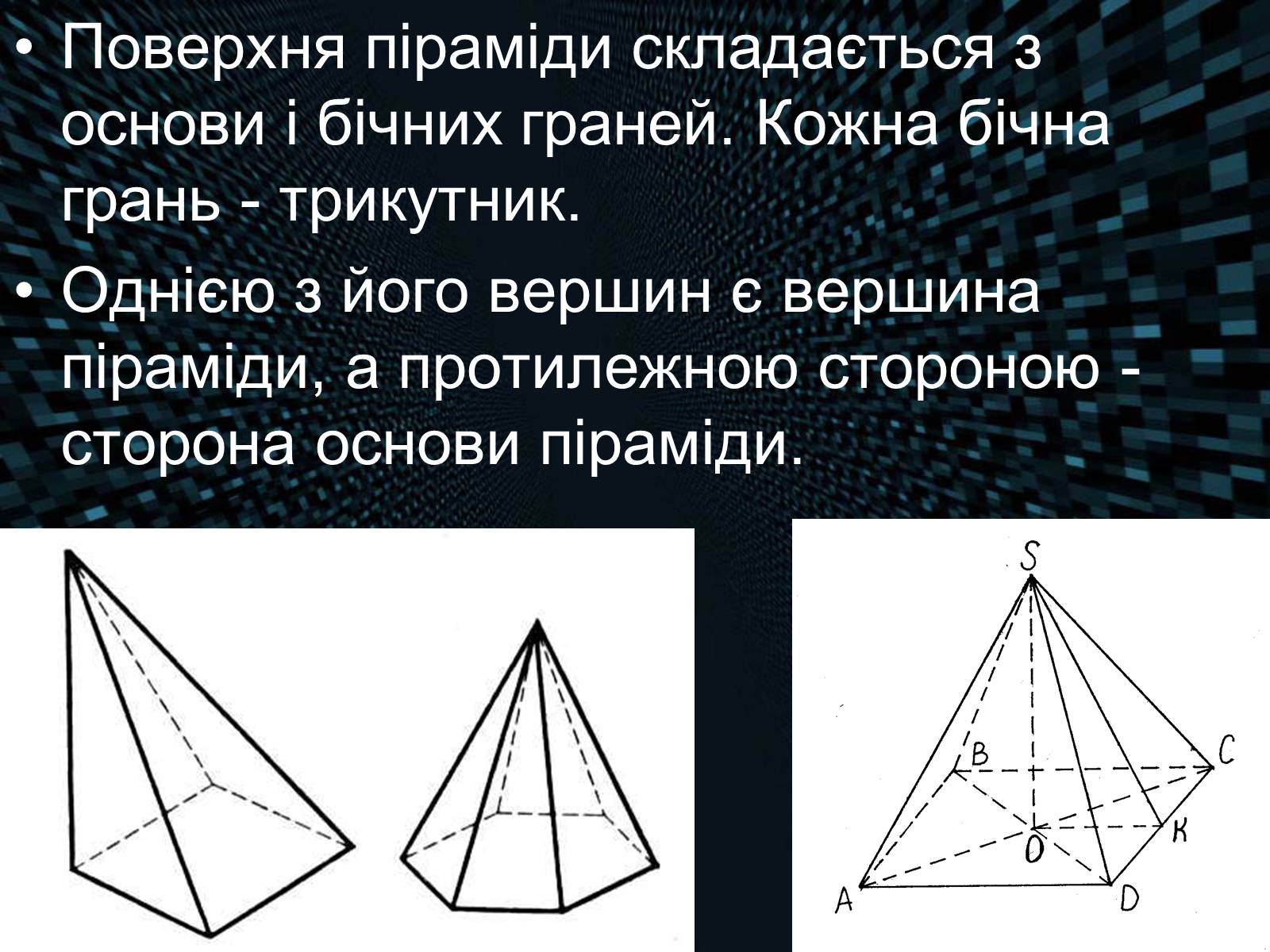
Поверхня піраміди складається з основи і бічних граней. Кожна бічна грань - трикутник.
Однією з його вершин є вершина піраміди, а протилежною стороною - сторона основи піраміди.
Однією з його вершин є вершина піраміди, а протилежною стороною - сторона основи піраміди.
Слайд #4
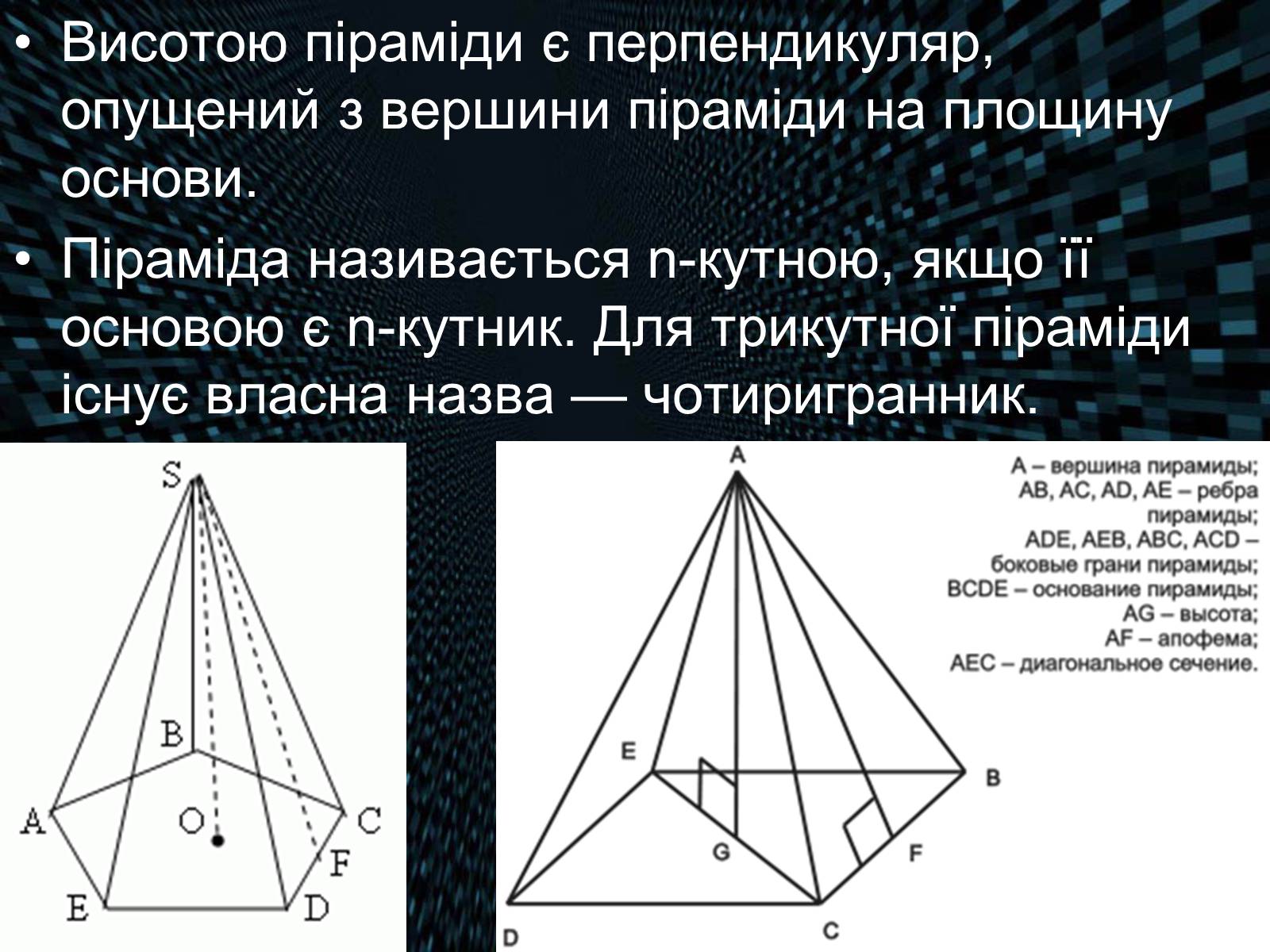
Висотою піраміди є перпендикуляр, опущений з вершини піраміди на площину основи.
Піраміда називається n-кутною, якщо її основою є n-кутник. Для трикутної піраміди існує власна назва — чотиригранник.
Піраміда називається n-кутною, якщо її основою є n-кутник. Для трикутної піраміди існує власна назва — чотиригранник.
Слайд #5
Правильна піраміда (довершена) — якщо її основою є правильний багатокутник, центр якого збігається з основою висоти піраміди.
Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.
Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.

Слайд #6
Вісь правильної піраміди — пряма, яка містить її висоту. У правильній піраміді бічні ребра рівні між собою, а бічні грані — рівні рівнобедрені трикутники.
Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Бічною поверхнею піраміди називається сума площ її бічних граней.
Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Бічною поверхнею піраміди називається сума площ її бічних граней.

Слайд #7
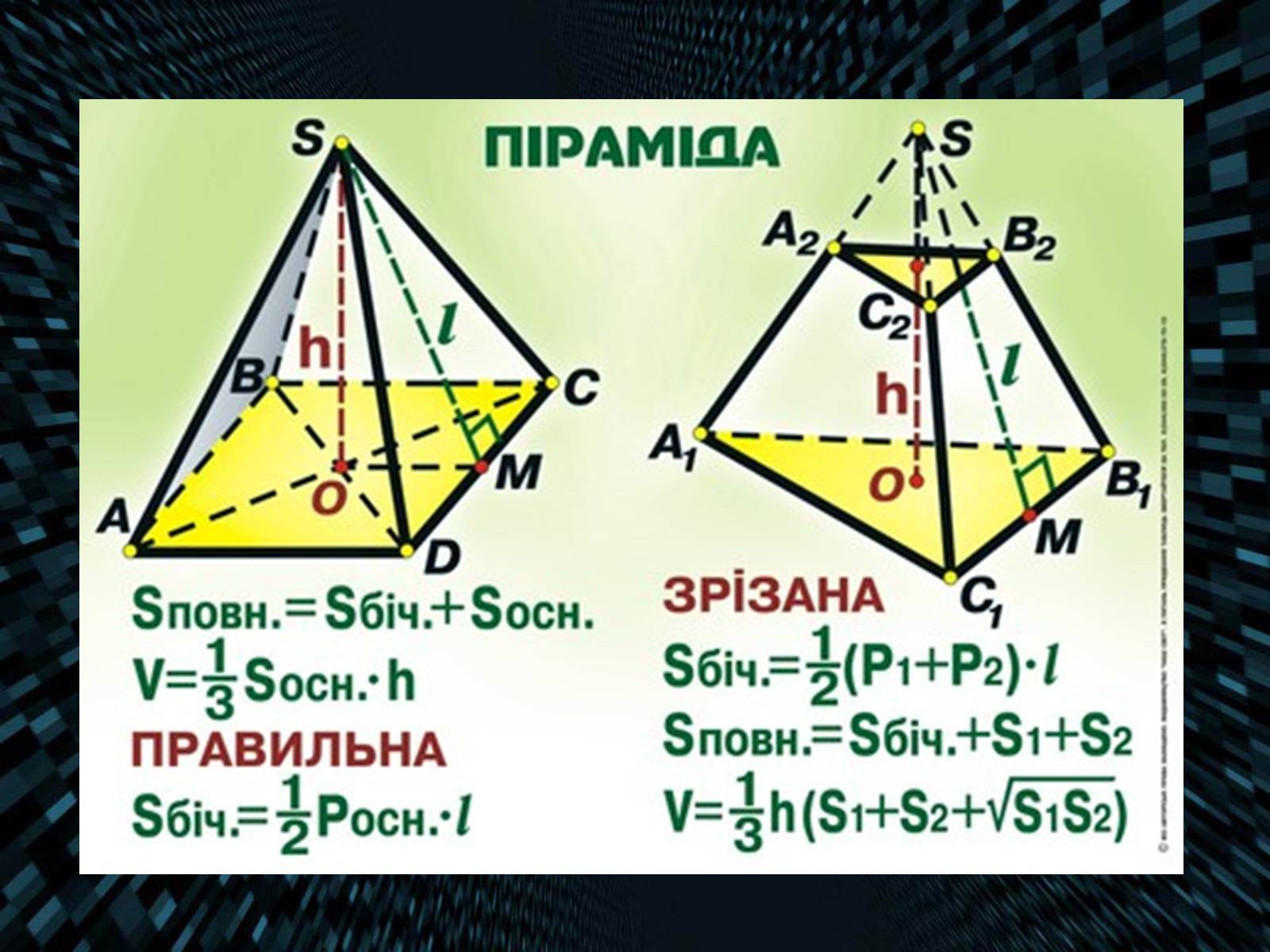
Площа бічної поверхні правильної піраміди дорівнює одній другій добутку периметра основи на апофему:
(тут Р — периметр, l — апофема, n — число сторін основи, b — бічне ребро, a — кут при вершині піраміди)
Об'єм піраміди дорівнює одній третій добутку площі її основи на висоту :
(тут Р — периметр, l — апофема, n — число сторін основи, b — бічне ребро, a — кут при вершині піраміди)
Об'єм піраміди дорівнює одній третій добутку площі її основи на висоту :

Слайд #8
Властивості правильної піраміди
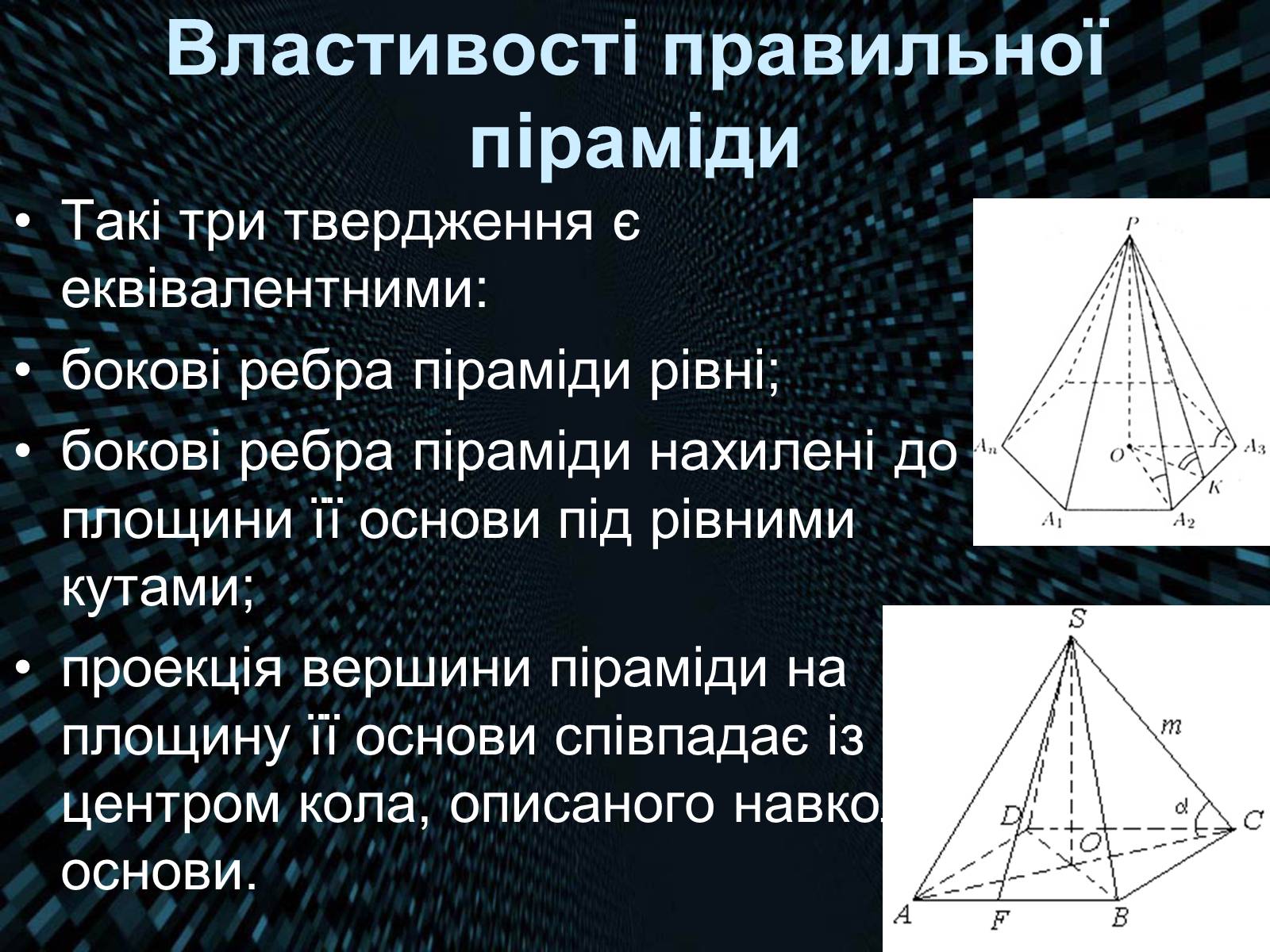
Такі три твердження є еквівалентними:
бокові ребра піраміди рівні;
бокові ребра піраміди нахилені до площини її основи під рівними кутами;
проекція вершини піраміди на площину її основи співпадає із центром кола, описаного навколо основи.
Такі три твердження є еквівалентними:
бокові ребра піраміди рівні;
бокові ребра піраміди нахилені до площини її основи під рівними кутами;
проекція вершини піраміди на площину її основи співпадає із центром кола, описаного навколо основи.
Слайд #9
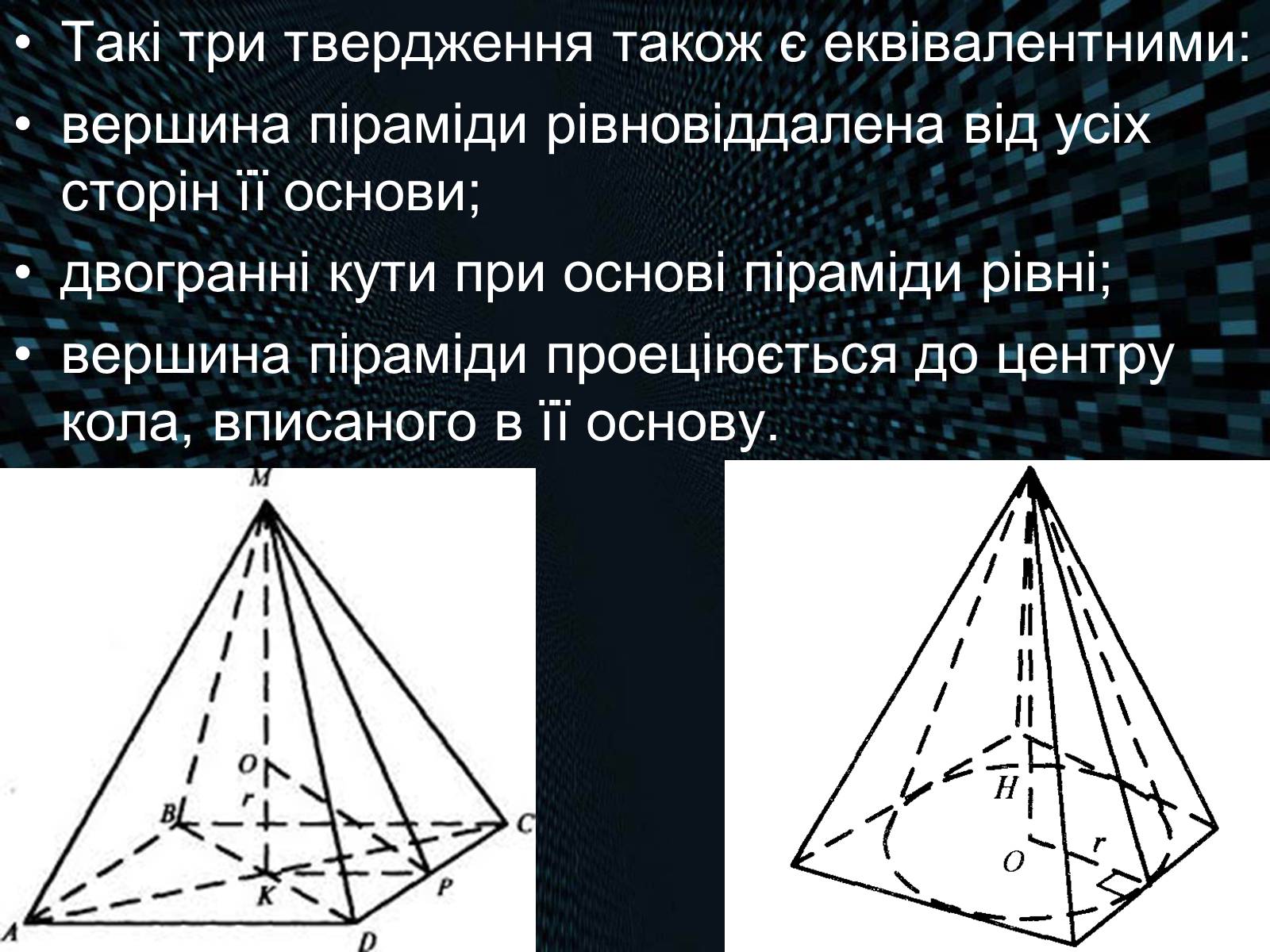
Такі три твердження також є еквівалентними:
вершина піраміди рівновіддалена від усіх сторін її основи;
двогранні кути при основі піраміди рівні;
вершина піраміди проеціюється до центру кола, вписаного в її основу.
вершина піраміди рівновіддалена від усіх сторін її основи;
двогранні кути при основі піраміди рівні;
вершина піраміди проеціюється до центру кола, вписаного в її основу.
Слайд #10
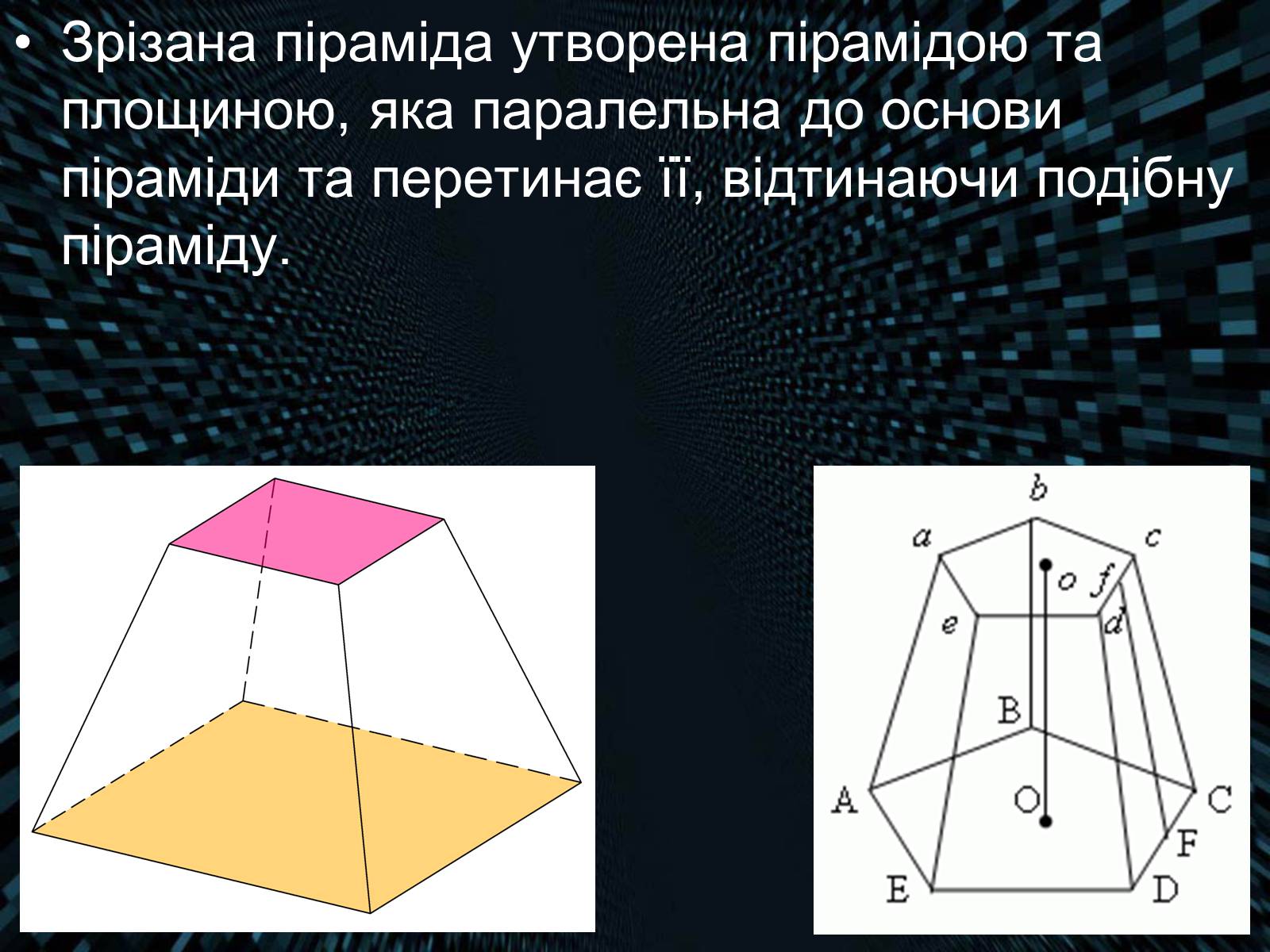
Зрізана піраміда утворена пірамідою та площиною, яка паралельна до основи піраміди та перетинає її, відтинаючи подібну піраміду.
Слайд #11
Зрізана піраміда утворена пірамідою та площиною, яка паралельна до основи піраміди та перетинає її, відтинаючи подібну піраміду.
Слайд #12
Піраміди в нашому житті
Піраміди в Мексиці - приклад зрізаної піраміди
Пакетик чая - приклад піраміди
Піраміди в Мексиці - приклад зрізаної піраміди
Пакетик чая - приклад піраміди

Слайд #13
Піраміда біля Лувра в Парижі

Слайд #14
Єгипетські піраміди
Пакет молока
Пакет молока

Слайд #15
Трикутний кубік Рубіка Горщик для квітів

Слайд #16
Урна Вуличний ліхтар

Слайд #17
Дитяча піраміда
