Презентація на тему «Правильні многогранники» (варіант 4)

…
«Правильні многогранники»

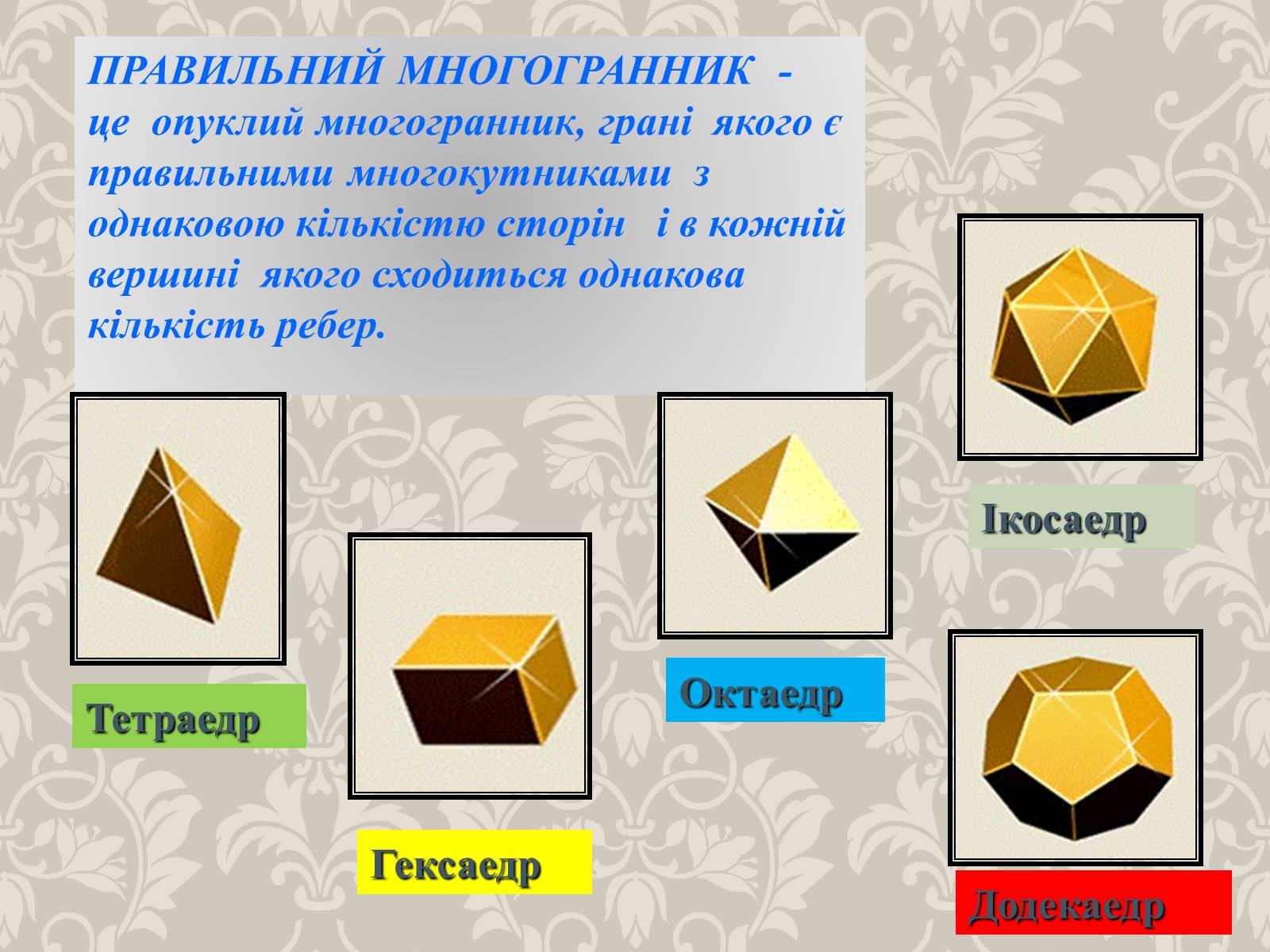
ПРАВИЛЬНИЙ МНОГОГРАННИК - це опуклий многогранник, грані якого є правильними многокутниками з однаковою кількістю сторін і в кожній вершині якого сходиться однакова кількість ребер.
Тетраедр
Гексаедр
Октаедр
Ікосаедр
Додекаедр

ТЕТРАЕДР
Правильним тетраедром називається многранник у якого всі грані – правильні трикутники і в кожній вершині сходиться 3 ребра.
Кількісні характеристики:
Вершин – 4
Ребер – 6
Граней – 4

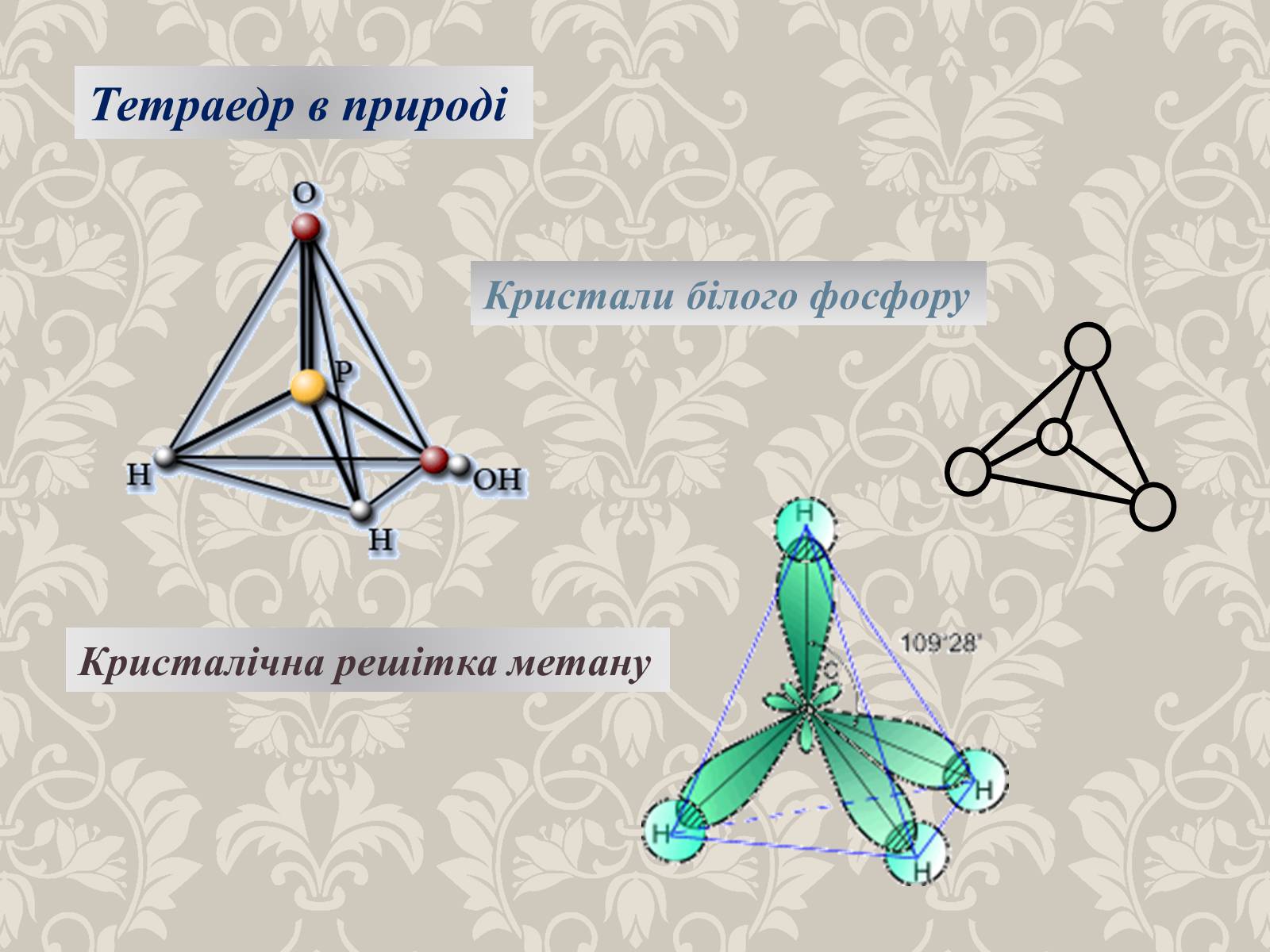
Тетраедр в природі
Кристали білого фосфору
Кристалічна решітка метану

ГЕКСАЕДР
У куба всі грані – квадрати, у кожній вершині сходиться по три ребра.
Куб – це прямокутний паралелепіпед, у якого всі ребра рівні.
Граней – 6
Ребер – 12
Вершин - 8
Кількісні характеристики:

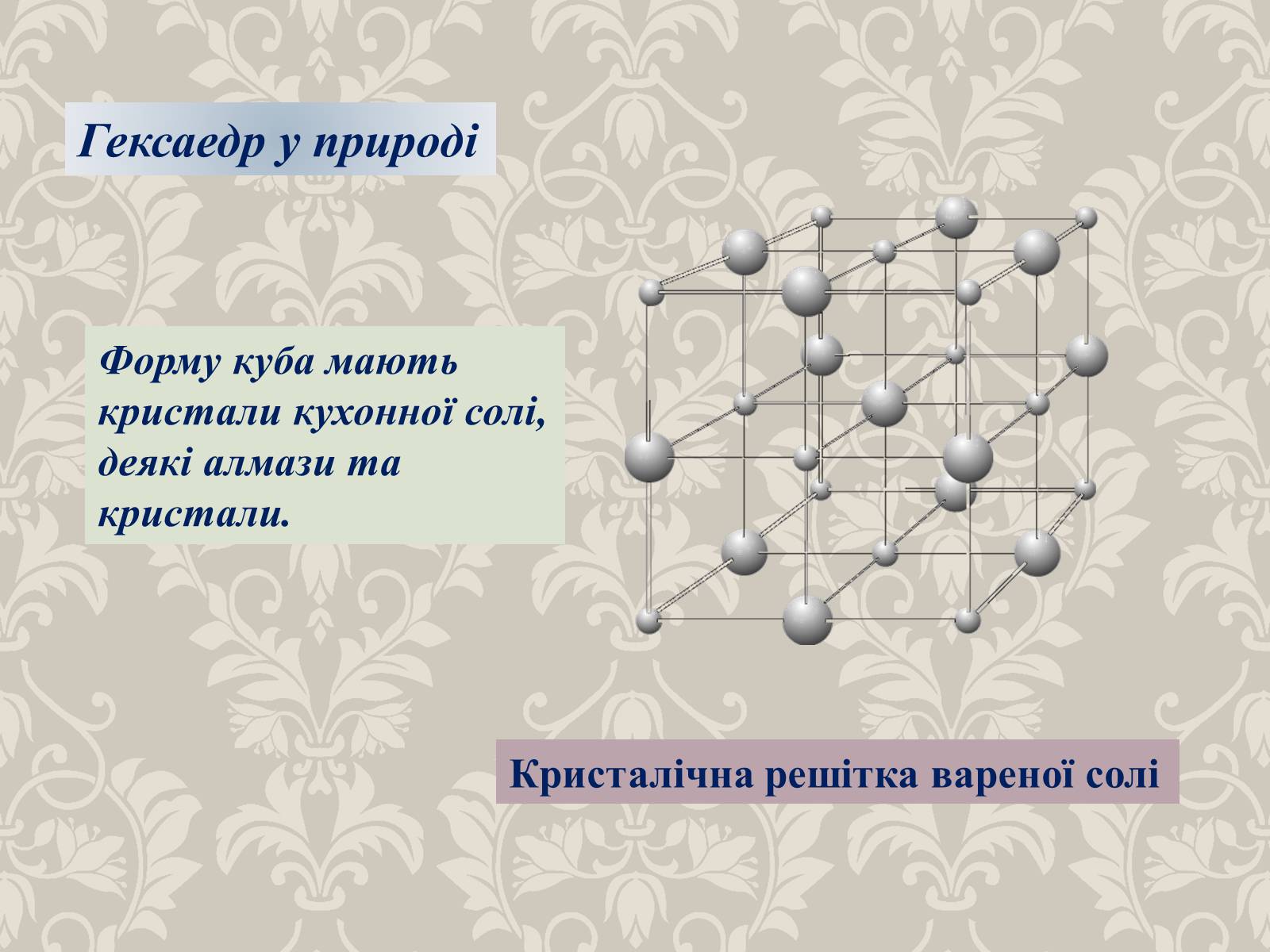
Гексаедр у природі
Кристалічна решітка вареної солі
Форму куба мають кристали кухонної солі, деякі алмази та кристали.

ОКТАЕДР
Октаедр – це правильний многогранник, у якого грані – правильні трикутники і в кожній вершині сходяться чотири ребра.
Кількісні характеристики:
Граней – 8
Вершин – 6
Ребер - 12

Октаедр в природі
Вуглець С характеризується структурою октаедра
Кристали алмаза

ІКОСАЕДР
Ікосаедр – правильний многогранник, грані якого – правильні трикутники і в кожній вершині сходиться по 5 ребер.
Кількісні характеристики
Вершин – 12
Ребер – 30
Граней - 20

Ікосаедр в природі
Кристал бору має форму ікосаедра
У біології німецький біолог
початку ХХ століття Еге Геккель
дослідив,що одноклітинні
організми – феодарії, точно
передають форму ікосаедра

ДОДЕКАЕДР
Додекаедр – це такий правильний многогранник, грані якого – правильні п'ятикутники і в кожній вершині сходиться по 3 ребра.
Кількісні характеристики:
Вершин – 20
Ребер – 30
Граней - 12

Додекаедр в природі
Вірус поліомієліту
Молекула ДНК складається з взаємовідносин ікосаедрів та додекаедрів

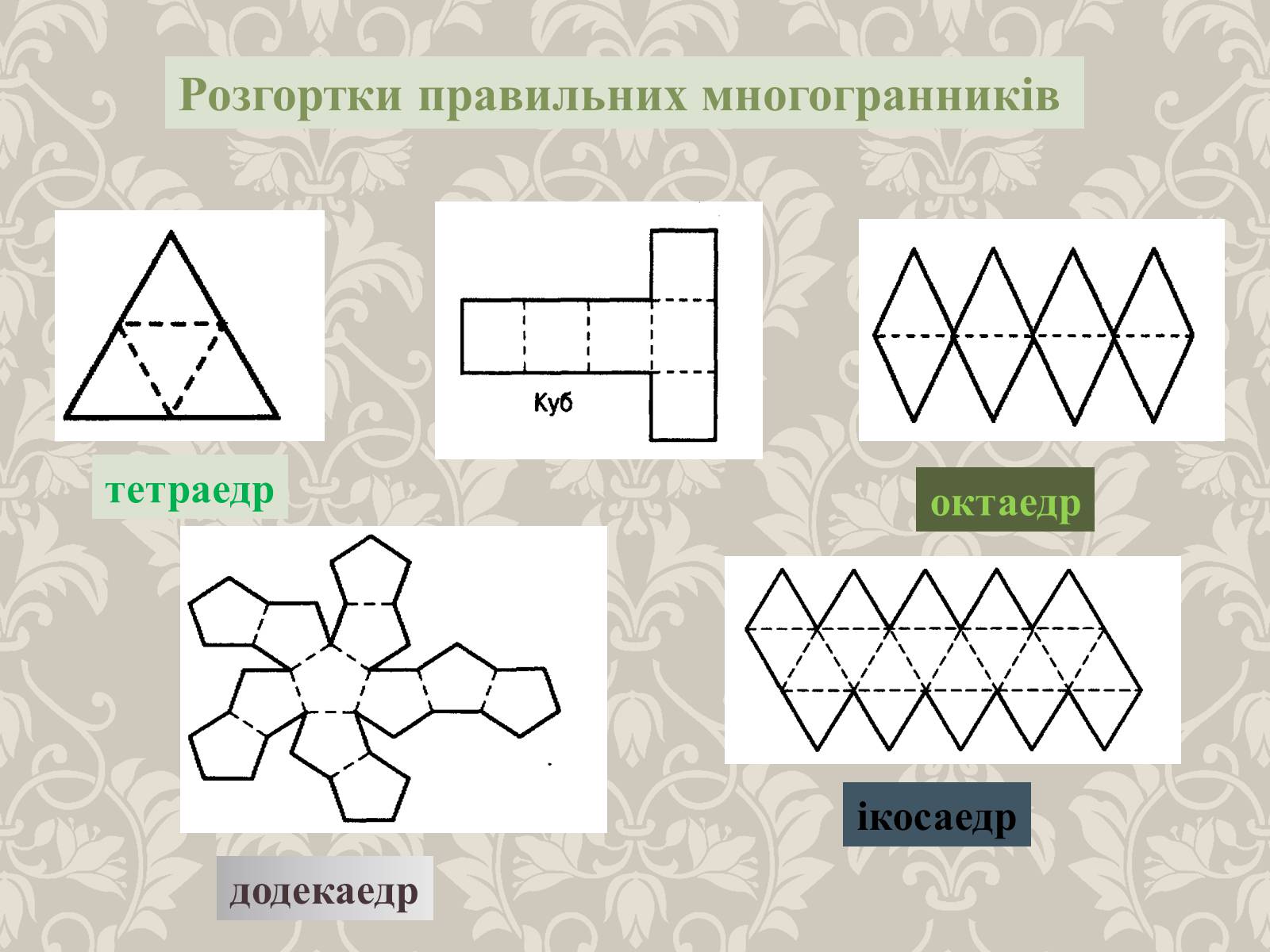
Розгортки правильних многогранників
тетраедр
октаедр
додекаедр
ікосаедр

Великий давньогрецький вчений Платон , що жив у IV -V ст. до н. е. . , вважав , що ці тіла уособлюють сутність природи . Людству були відомі чотири сутності: вогонь , вода , земля і повітря . На думку Платона їх атоми мали вигляд правильних багатогранників : вогню - тетраедр , землі - гексаедр , повітря - октаедр , води - ікосаедр . Ця теорія була викладена в роботі "Діалог Тімей " . Платон припустив , що існує ще одна сутність- світовий ефір , атоми якого мають вигляд додекаедра . Платон і його учні в своїх роботах приділяли велику увагу правильних багатогранників , і їх тому ще називають " Платоновими тілами "

Геометрія з її прозорою логікою, чіткістю побудов відкрила
зовсім нове бачення правильних многогранників та їх
нове застосування.