Презентація на тему «Пирамида»

Пирамида

Что такое пирамида?
Пирамида  — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.

История развития пирамиды в геометрии.
Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Первый, кто установил, чему равен объем пирамиды, был Демокрит, а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды:
Телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.
Демокрит
Евдокс Книдский
Евклид

Элементы пирамиды
апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины;
боковые грани (1) — треугольники сходящиеся в вершине
боковые ребра (2)
вершина пирамиды (3) — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;
высота (4)— отрезок перпендикуляра, проведённого
через вершину пирамиды к плоскости её основания
(концами этого отрезка являются вершина
пирамиды и основание перпендикуляра);
диагональное сечение пирамиды — сечение
пирамиды, проходящее через вершину и
диагональ основания;
основание (5) — многоугольник, которому не
принадлежит вершина пирамиды;

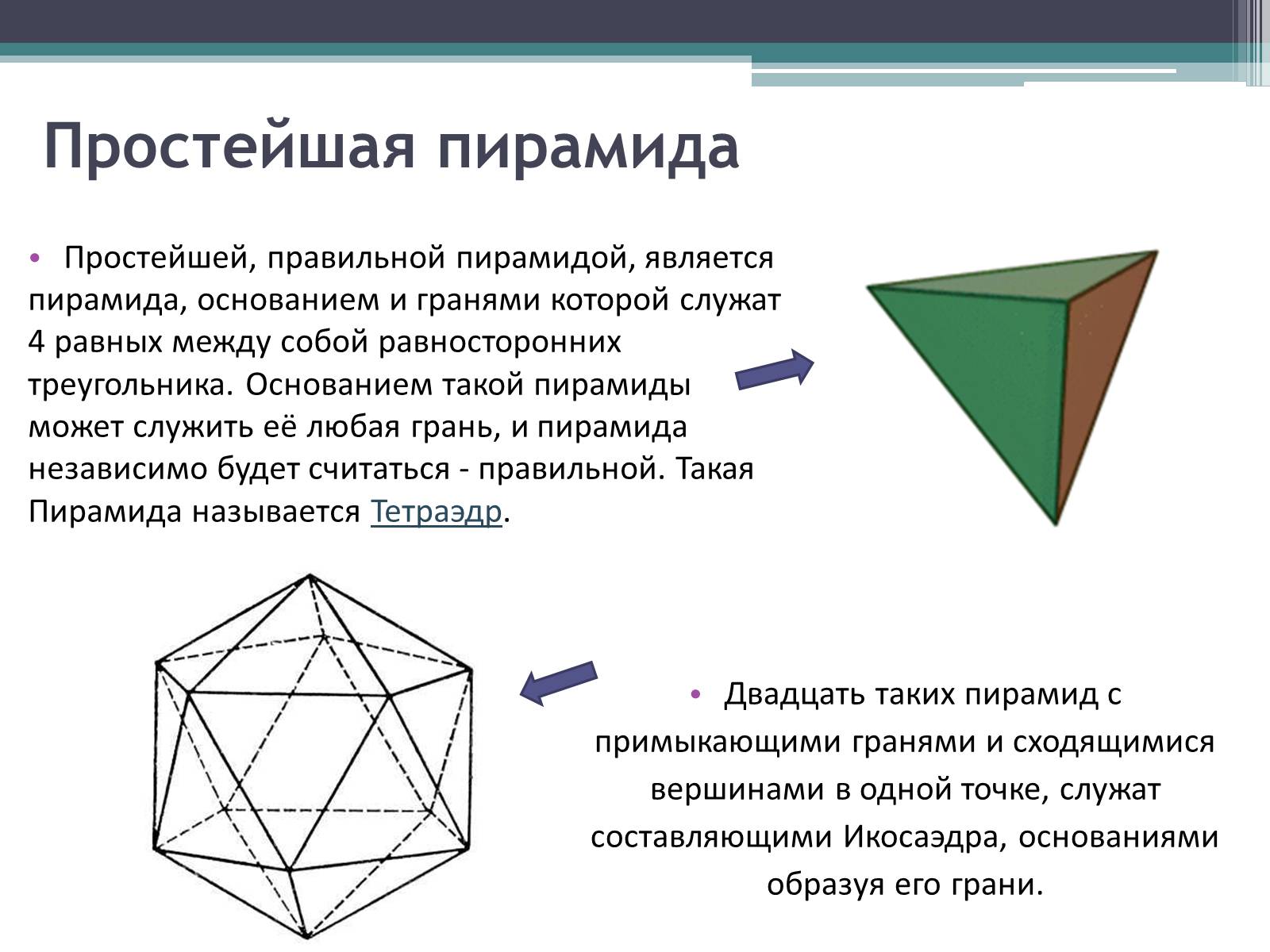
Простейшая пирамида
Простейшей, правильной пирамидой, является
пирамида, основанием и гранями которой служат
4 равных между собой равносторонних
треугольника. Основанием такой пирамиды
может служить её любая грань, и пирамида
независимо будет считаться - правильной. Такая
Пирамида называется Тетраэдр.
Двадцать таких пирамид с
примыкающими гранями и сходящимися
вершинами в одной точке, служат
составляющими Икосаэдра, основаниями
образуя его грани.

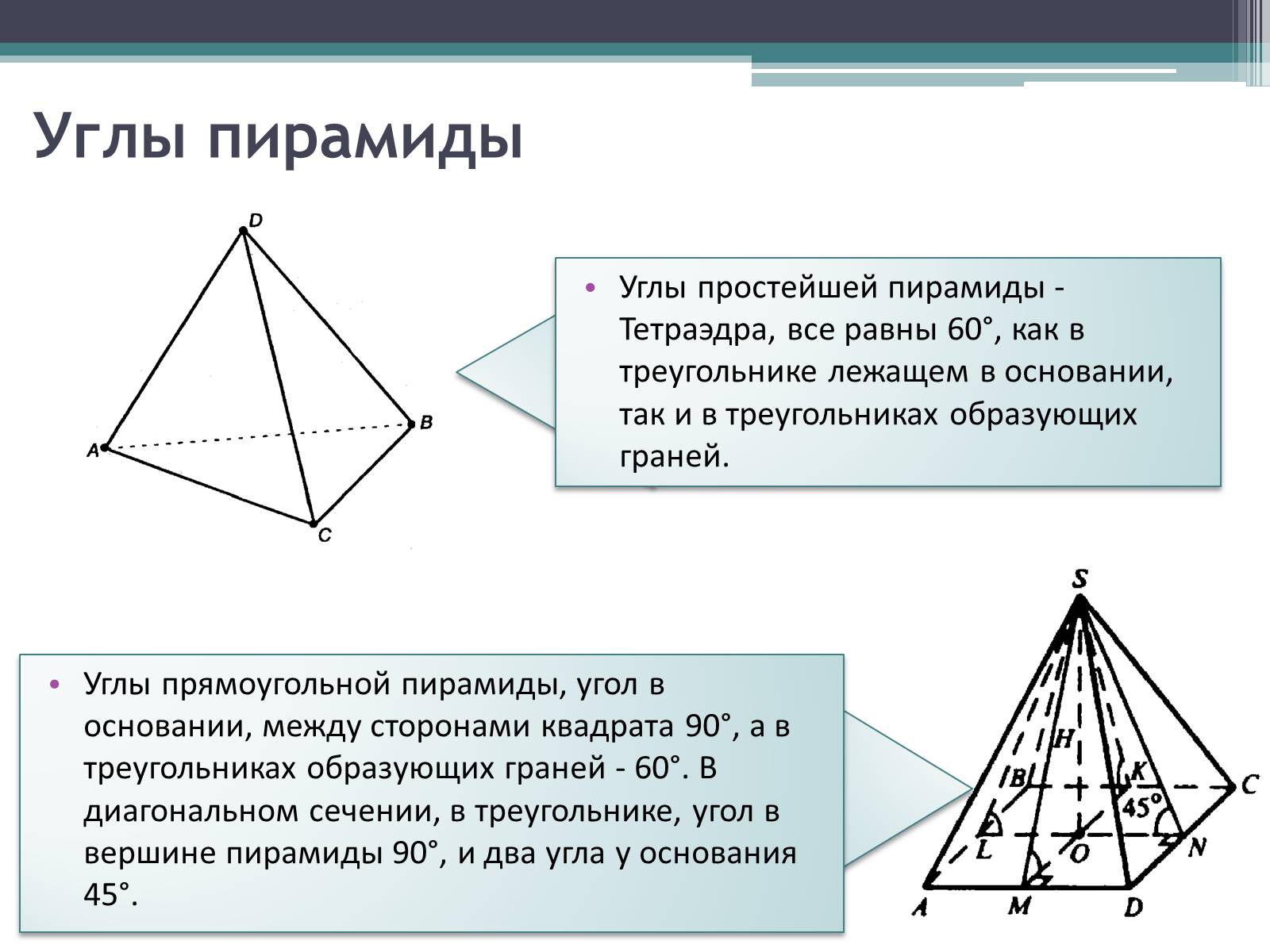
Углы пирамиды
Углы простейшей пирамиды - Тетраэдра, все равны 60°, как в треугольнике лежащем в основании, так и в треугольниках образующих граней.
Углы прямоугольной пирамиды, угол в основании, между сторонами квадрата 90°, а в треугольниках образующих граней - 60°. В диагональном сечении, в треугольнике, угол в вершине пирамиды 90°, и два угла у основания 45°.

Развёртка пирамиды
Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с плоскостью. Если отсек фигуры поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру — ее разверткой.
Разверткой Тетраэдра, будет равносторонний как основание, и такие же равносторонние присоединенные обшей стороной к сторонам основания.
Разверткой правильной прямоугольной пирамиды, будет основание, и четыре равносторонних (грани), имеющие с основанием общую сторону с основанием.
Разверткой правильной пятигранной пирамиды, будет правильный пятиугольник в основании, и 5 равнобедренных , имеющих общую сторону с основанием.

Свойства пирамиды
Если все боковые ребра равны, то:
около основания пирамиды можно описать окружность,
вершина пирамиды проецируется в её центр;
боковые ребра образуют с плоскостью основания равные
углы.
также верно и обратное, т. е. если боковые ребра образуют
с плоскостью основания равные углы или если около основания
пирамиды можно описать окружность, причём вершина пирамиды проецируется
в её центр, то все боковые ребра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом, то:
около основания пирамиды можно описать окружность, вершина пирамиды проецируется в её центр;
боковые ребра образуют с плоскостью основания равные углы.
также верно и обратное, т. е. если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

Формулы, связанные с пирамидой
Объём пирамиды может быть вычислен по формуле:
где S — площадь основания и  h — высота;
Также объём треугольной пирамиды (тетраэдра) может быть вычислен по формуле:
где a1,a2— скрещивающиеся рёбра, d — расстояние между a1 и a2 , — угол между a1 и a2;
 
Боковая поверхность — это сумма площадей боковых граней:

Формулы, связанные с пирамидой
Полная поверхность — это сумма площади боковой поверхности и площади основания:
Для нахождения боковой поверхности в правильной пирамиде можно использовать формулы:
где  a — апофема, P — периметр основания, n — число сторон основания, b — боковое ребро,  — плоский угол при вершине пирамиды.

Особые случаи пирамиды
Правильная пирамида
Пирамида называется правильной, если
основанием её является правильный многоугольник, а вершина
проецируется в центр основания.
Тогда она обладает такими свойствами:
боковые ребра правильной пирамиды равны;
в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;
в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;
если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна , а каждый из них соответственно , где n — количество сторон многоугольника основания;
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Прямоугольная пирамида
Пирамида называется прямоугольной, если одно из боковых
рёбер пирамиды перпендикулярно основанию. В данном
случае, это ребро и является высотой пирамиды.
Особые случаи пирамиды

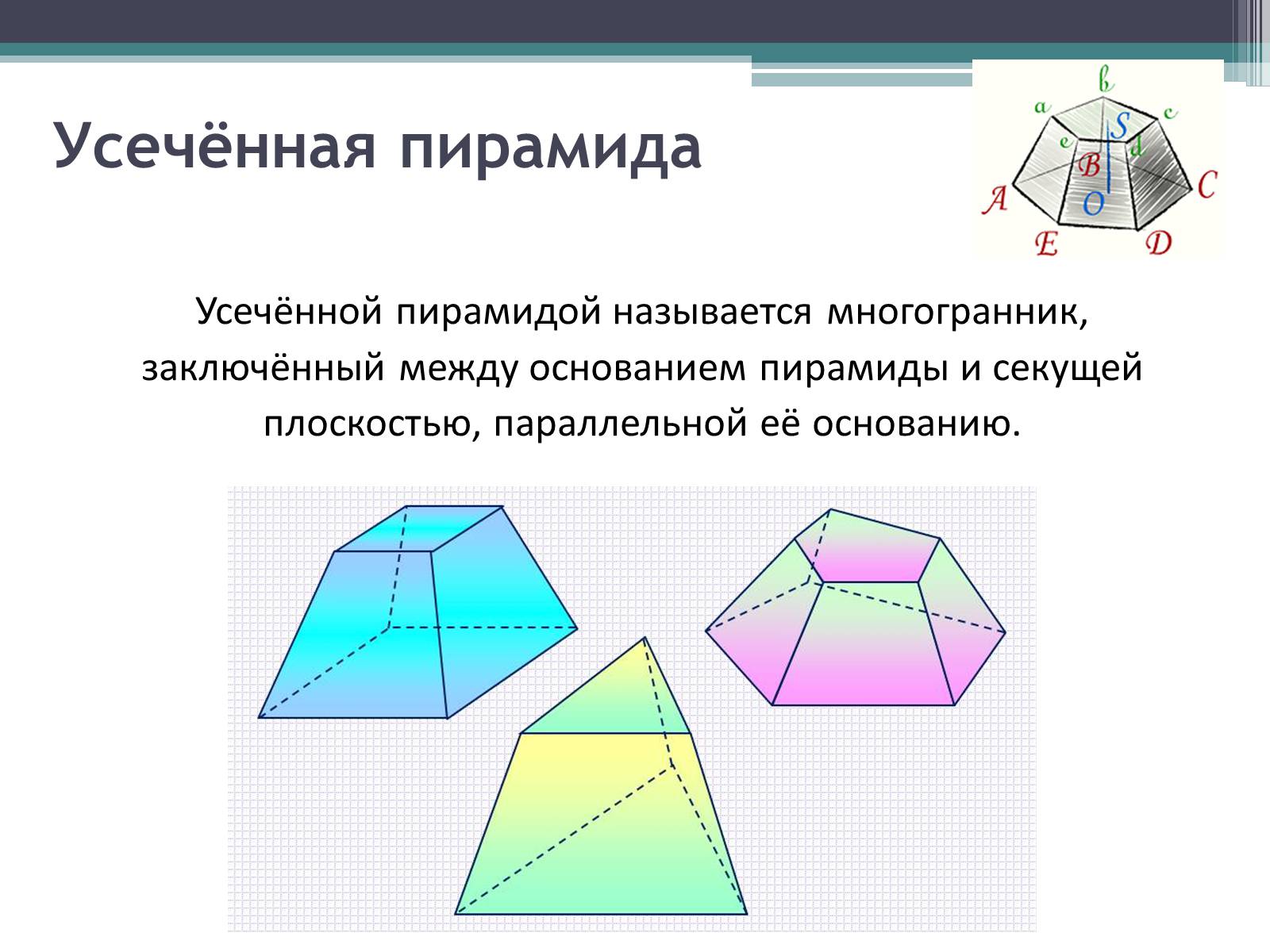
Усечённая пирамида
Усечённой пирамидой называется многогранник,
заключённый между основанием пирамиды и секущей
плоскостью, параллельной её основанию.

Интересные факты
Формула для расчёта объёма усечённой пирамиды была выведена раньше, чем для полной.

Пирамиды в жизни

СПАСИБО ЗА ВНИМАНИЕ!