- Головна
- Готові шкільні презентації
- Презентація на тему «Комбинации и бином Ньютона»
Презентація на тему «Комбинации и бином Ньютона»
497
Слайд #1
Комбинации и бином Ньютона
Выполнили:
Выполнили:

Слайд #2
Комбинации
Мы иногда делаем выбор из множества без учета порядка . Такой выбор называется комбинацией. Если вы играете в карты, например, вы знаете, что в большинстве ситуаций порядок, в котором вы держите карты, не имеет значения.
Существуют 3 вида комбинаций составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству (например, буквы алфавита, книги в библиотеке, машины на стоянке и т.д.):
Перестановки
Размещения
Сочетания
Мы иногда делаем выбор из множества без учета порядка . Такой выбор называется комбинацией. Если вы играете в карты, например, вы знаете, что в большинстве ситуаций порядок, в котором вы держите карты, не имеет значения.
Существуют 3 вида комбинаций составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству (например, буквы алфавита, книги в библиотеке, машины на стоянке и т.д.):
Перестановки
Размещения
Сочетания

Слайд #3
Перестановки
Возьмём n различных элементов: a1 , a2 , a3 , …, an . Будем переставлять их всеми возможными способами, сохраняя их количество и меняя лишь порядок их расположения. Каждая из полученных таким образом комбинаций называется перестановкой. Общее количество перестановок из n элементов обозначается Pn . Это число равно произведению всех целых чисел от 1 до n :
Символ n! ( называется факториал ) - сокращённая запись произведения: 1 · 2 · 3 · … · ( n – 1 ) · n .
П р и м е р 1. Найти число перестановок из трёх элементов: a, b, c.
Р е ш е н и е . В соответствии с приведенной формулой: P3 = 1 · 2 · 3 =6.
Действительно, мы имеем 6 перестановок: abc, acb, bac, bca, cab, cba.
Возьмём n различных элементов: a1 , a2 , a3 , …, an . Будем переставлять их всеми возможными способами, сохраняя их количество и меняя лишь порядок их расположения. Каждая из полученных таким образом комбинаций называется перестановкой. Общее количество перестановок из n элементов обозначается Pn . Это число равно произведению всех целых чисел от 1 до n :
Символ n! ( называется факториал ) - сокращённая запись произведения: 1 · 2 · 3 · … · ( n – 1 ) · n .
П р и м е р 1. Найти число перестановок из трёх элементов: a, b, c.
Р е ш е н и е . В соответствии с приведенной формулой: P3 = 1 · 2 · 3 =6.
Действительно, мы имеем 6 перестановок: abc, acb, bac, bca, cab, cba.

Слайд #4
Размещения
Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, располагая эти m взятых элементов в различном порядке. Полученные комбинации называются размещениями из n элементов по m .
Их общее количество обозначается: и равно произведению:
П р и м е р 2. Найти число размещений из четырёх элементов a, b, c, d по два.
Р е ш е н и е . В соответствии с формулой получим:
Вот эти размещения: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.
Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, располагая эти m взятых элементов в различном порядке. Полученные комбинации называются размещениями из n элементов по m .
Их общее количество обозначается: и равно произведению:
П р и м е р 2. Найти число размещений из четырёх элементов a, b, c, d по два.
Р е ш е н и е . В соответствии с формулой получим:
Вот эти размещения: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.

Слайд #5
Сочетания
Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, не принимая во внимание порядок расположения этих m элементов. Тогда мы получим сочетания из n элементов по m .
Их общее количество обозначается и может быть вычислено по формуле:
Из этой формулы ясно, что
Заметим, что можно составить только одно сочетание из n элементов по n , которое содержит все n элементов. Формула числа сочетаний даёт это значение, если только принять, что 0! = 1, что является определением 0! .
В соответствии с этим определением получим:
Общее число сочетаний можно вычислить, пользуясь и другим выражением:
Будем составлять группы из m различных элементов, взятых из множества, состоящего из n элементов, не принимая во внимание порядок расположения этих m элементов. Тогда мы получим сочетания из n элементов по m .
Их общее количество обозначается и может быть вычислено по формуле:
Из этой формулы ясно, что
Заметим, что можно составить только одно сочетание из n элементов по n , которое содержит все n элементов. Формула числа сочетаний даёт это значение, если только принять, что 0! = 1, что является определением 0! .
В соответствии с этим определением получим:
Общее число сочетаний можно вычислить, пользуясь и другим выражением:

Слайд #6
П р и м е р 3 . Найти число сочетаний из пяти элементов: a, b, c, d, e по три.
Р е ш е н и е :
Эти сочетания: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.
Р е ш е н и е :
Эти сочетания: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

Слайд #7
Бином Ньютона.
-биномиальные коэффициенты
Это формула, представляющая выражение
( a + b ) n при положительном целом n в виде многочлена:
Заметим, что сумма показателей степеней для a и b постоянна и равна n.
-биномиальные коэффициенты
Это формула, представляющая выражение
( a + b ) n при положительном целом n в виде многочлена:
Заметим, что сумма показателей степеней для a и b постоянна и равна n.

Слайд #8
Рассмотрим следующие выражения со степенями (a + b)n, где a + b есть любой бином, а n - целое число.

Слайд #9
Каждое выражение - это полином. Во всех выражениях можно заметить особенности.
1. В каждом выражении на одно слагаемое больше, чем показатель степени n.
2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.
3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.
4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до "половины пути", а потом уменьшаются на те же значения обратно к 1.
1. В каждом выражении на одно слагаемое больше, чем показатель степени n.
2. В каждом слагаемом сумма степеней равна n, т.е. степени, в которую возводится бином.
3. Степени начинаются со степени бинома n и уменьшаются к 0. Последний член не имеет множителя a. Первый член не имеет множителя b, т.е. степени b начинаются с 0 и увеличиваются до n.
4. Коэффициенты начинаются с 1 и увеличиваются на определенные значения до "половины пути", а потом уменьшаются на те же значения обратно к 1.

Слайд #10
Давайте рассмотрим коэффициенты подробнее. Предположим, что мы хотим найти значение (a + b)6. Согласно особенности, которую мы только что заметили, здесь должно быть 7 членовa6 + c1a5b + c2a4b2 + c3a3b3 + c4a2b4 + c5ab5 + b6.Но как мы можем определить значение каждого коэффициента, ci? Мы можем сделать это двумя путями. Первый метод включает в себя написание коэффициентов треугольником, как показано ниже. Это известно как Треугольник Паскаля:

Слайд #11
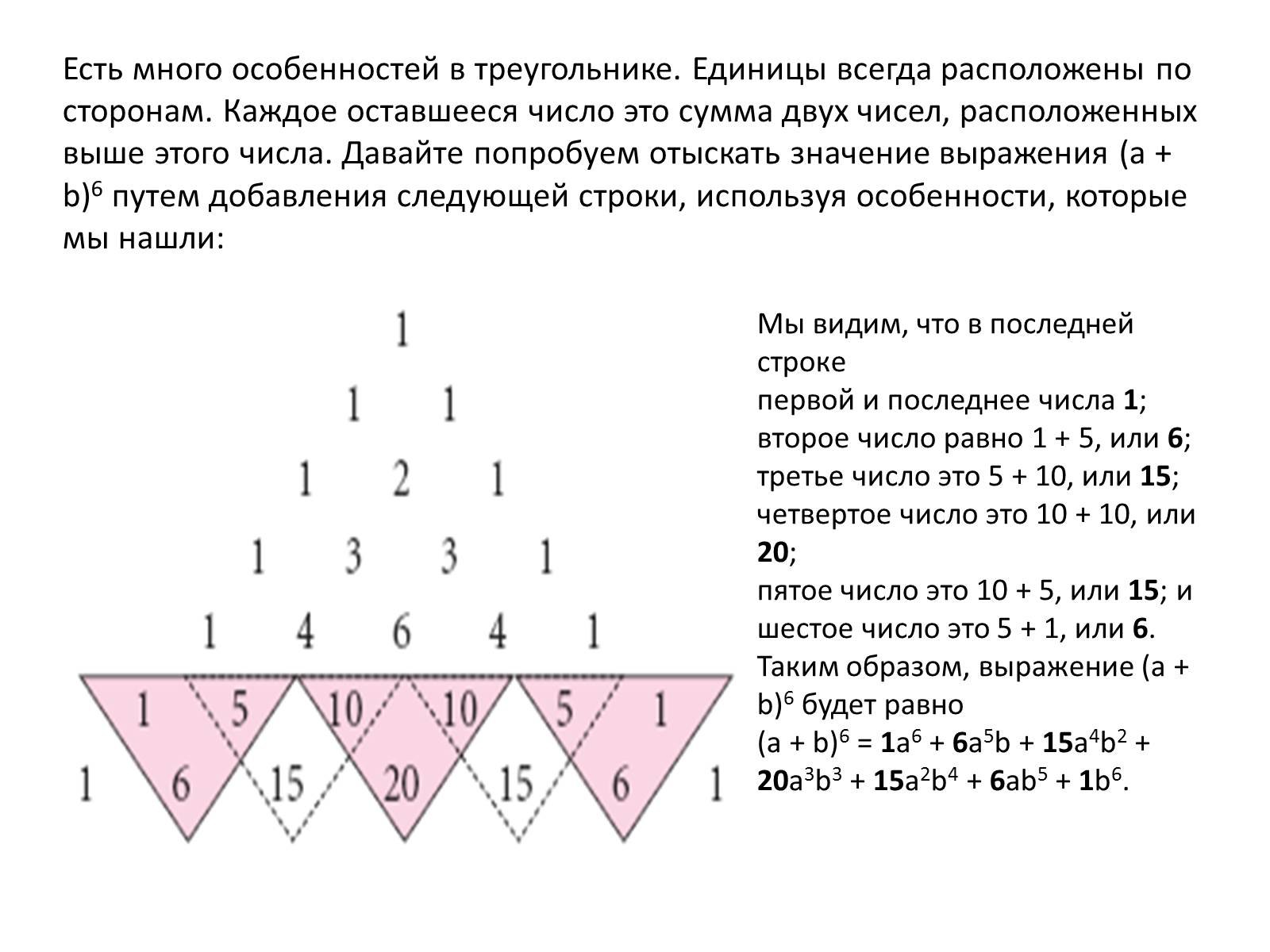
Есть много особенностей в треугольнике. Единицы всегда расположены по сторонам. Каждое оставшееся число это сумма двух чисел, расположенных выше этого числа. Давайте попробуем отыскать значение выражения (a + b)6 путем добавления следующей строки, используя особенности, которые мы нашли:
Мы видим, что в последней строке
первой и последнее числа 1;второе число равно 1 + 5, или 6;третье число это 5 + 10, или 15;четвертое число это 10 + 10, или 20;пятое число это 10 + 5, или 15; ишестое число это 5 + 1, или 6.
Таким образом, выражение (a + b)6 будет равно(a + b)6 = 1a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + 1b6.
Мы видим, что в последней строке
первой и последнее числа 1;второе число равно 1 + 5, или 6;третье число это 5 + 10, или 15;четвертое число это 10 + 10, или 20;пятое число это 10 + 5, или 15; ишестое число это 5 + 1, или 6.
Таким образом, выражение (a + b)6 будет равно(a + b)6 = 1a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + 1b6.
Слайд #12
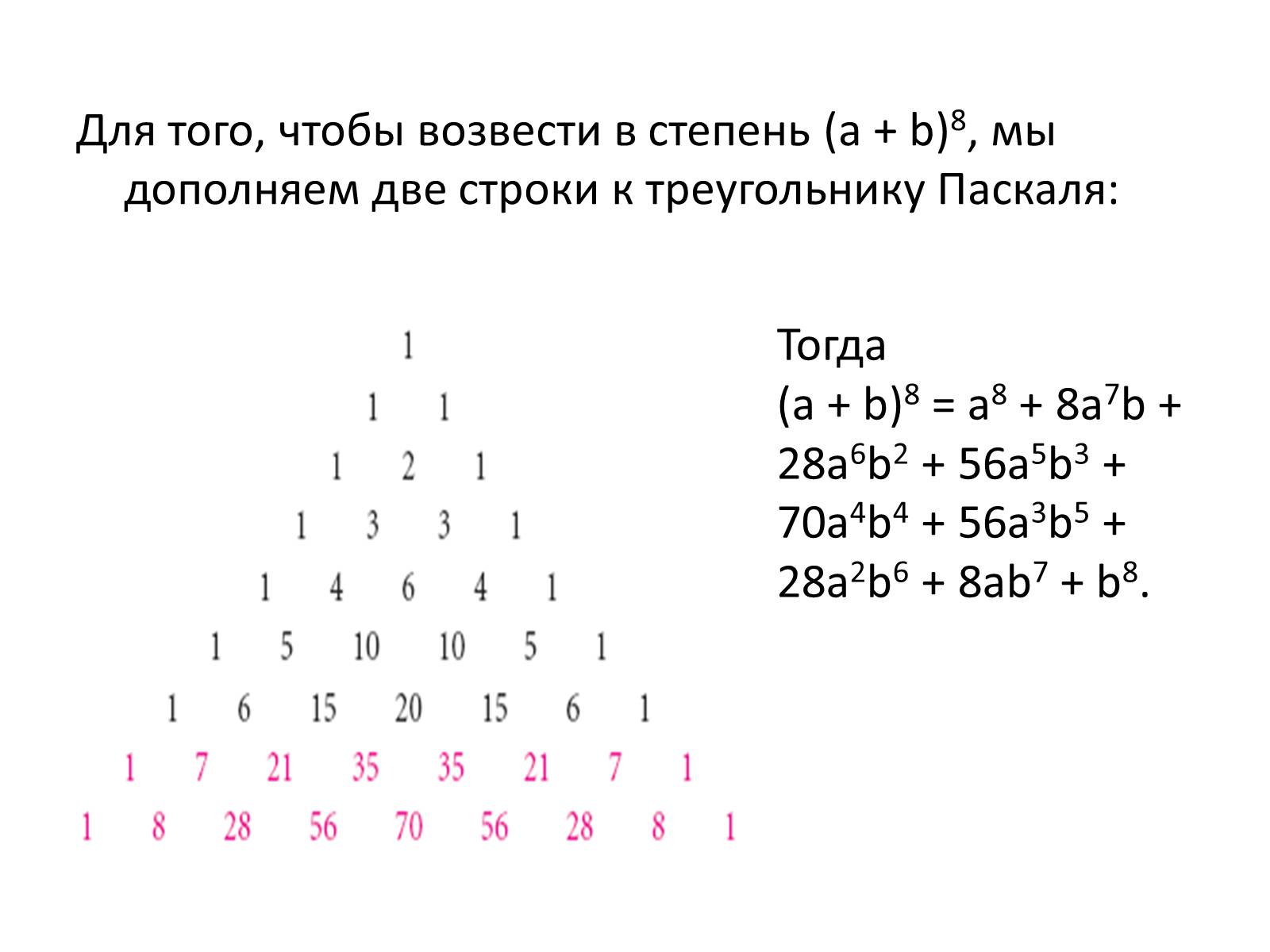
Для того, чтобы возвести в степень (a + b)8, мы дополняем две строки к треугольнику Паскаля:
Тогда (a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + 28a2b6 + 8ab7 + b8.
Тогда (a + b)8 = a8 + 8a7b + 28a6b2 + 56a5b3 + 70a4b4 + 56a3b5 + 28a2b6 + 8ab7 + b8.
Слайд #13
Пример 1 Возведите в степень: (u - v)5.
Решение У нас есть (a + b)n, где a = u, b = -v, и n = 5. Мы используем 6-й ряд треугольника Паскаля:1 5 10 10 5 1Тогда у нас есть(u - v)5 = [u + (-v)]5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5 - 5u4v + 10u3v2 - 10u2v3 + 5uv4 - v5.Обратите внимание, что знаки членов колеблются между + и -. Когда степень -v есть нечетным числом, знак -.
Решение У нас есть (a + b)n, где a = u, b = -v, и n = 5. Мы используем 6-й ряд треугольника Паскаля:1 5 10 10 5 1Тогда у нас есть(u - v)5 = [u + (-v)]5 = 1(u)5 + 5(u)4(-v)1 + 10(u)3(-v)2 + 10(u)2(-v)3 + 5(u)(-v)4 + 1(-v)5 = u5 - 5u4v + 10u3v2 - 10u2v3 + 5uv4 - v5.Обратите внимание, что знаки членов колеблются между + и -. Когда степень -v есть нечетным числом, знак -.

Слайд #14
Пример 2 Возведите в степень: (x2 - 2y)5.
Решение У нас есть (a + b)n, где a = x2, b = -2y, и n = 5. Тогда, используя бином Ньютона, мы имеем
Наконец, (x2 - 2y)5 = x10 - 10x8y + 40x6y2 - 80x4y3 + 80x2y4 - 35y5.
Решение У нас есть (a + b)n, где a = x2, b = -2y, и n = 5. Тогда, используя бином Ньютона, мы имеем
Наконец, (x2 - 2y)5 = x10 - 10x8y + 40x6y2 - 80x4y3 + 80x2y4 - 35y5.

Слайд #15
1. Сумма коэффициентов разложения ( a + b ) n равна 2 n .
Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:
2. Коэффициенты членов, равноудалённых от концов разложения, равны.
Это свойство следует из соотношения:
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна
Для доказательства воспользуемся биномом:
Здесь чётные члены имеют знак « + » , а нечётные - « - ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна:
что и требовалось доказать.
4. Коэффициенты находятся по треугольнику Паскаля.
Свойства биноминальных коэффициентов
Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:
2. Коэффициенты членов, равноудалённых от концов разложения, равны.
Это свойство следует из соотношения:
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна
Для доказательства воспользуемся биномом:
Здесь чётные члены имеют знак « + » , а нечётные - « - ». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна:
что и требовалось доказать.
4. Коэффициенты находятся по треугольнику Паскаля.
Свойства биноминальных коэффициентов
