- Головна
- Готові шкільні презентації
- Презентація на тему «Математика в медицині»
Презентація на тему «Математика в медицині»
311
Слайд #1
Математика в медицині

Слайд #2
План
Вступ
Тематичні питання:
Математичне моделювання в медицині
Математичні формули, які відображають процес передачі захворювання (Математична модель епідемії грипу)
«Золотий переріз». Здоров`я і гармонія
Висновок
Вступ
Тематичні питання:
Математичне моделювання в медицині
Математичні формули, які відображають процес передачі захворювання (Математична модель епідемії грипу)
«Золотий переріз». Здоров`я і гармонія
Висновок

Слайд #3
Вступ
Математика - це така важлива наука в нашому житті, що, практично в жодній сфері
трудової діяльності без неї не можна обійтися. Здавалося б, що математика в медицині не потрібна. Але-це не так. Щоб лікувати хворих потрібно вирахувати необхідно дозу ліків.
Доза буває разова, добова, курсова. Для того, щоб оцінити стан новонародженної
дитини і в подальшому призначити лікування, потрібно знати масово-ростовий коефіцієнт,
який визначається за допомогою математичних дій. При багатьох захворюваннях втрачається
рідина в організмі та різні мікроелементи. Щоб призначити таким хворим адекватне лікування
потрібно знати ступінь цієї втрати тобто ступінь ексікозу.
Математика - це така важлива наука в нашому житті, що, практично в жодній сфері
трудової діяльності без неї не можна обійтися. Здавалося б, що математика в медицині не потрібна. Але-це не так. Щоб лікувати хворих потрібно вирахувати необхідно дозу ліків.
Доза буває разова, добова, курсова. Для того, щоб оцінити стан новонародженної
дитини і в подальшому призначити лікування, потрібно знати масово-ростовий коефіцієнт,
який визначається за допомогою математичних дій. При багатьох захворюваннях втрачається
рідина в організмі та різні мікроелементи. Щоб призначити таким хворим адекватне лікування
потрібно знати ступінь цієї втрати тобто ступінь ексікозу.

Слайд #4
Для правильного вигодовування немовляти, потрібно вміти визначити кількість необхідної їжі та харчових добавок. В такій сфері, як травматологія за допомогою математики розраховується біомеханічні співвідношення кісток і суглобів. При лікуванні переломів потрібно правильно визначити довжину металевих пластин, гвинтів, шпиць, кути, під якими вони фіксуються. Важливо вміти розрахувати терміни імобілізації та початку фізичної активності ураженого сегменту.
Коли переломи лікуються за допомогою апарату зовнішньої фіксації, математично визначаються відстані між стержнями, величини компресії або дистракції . При накладанні гіпсових пов'язок необхідно правильно визначати кути фіксації кінцівок. Коли хвороби приводять до викривленя руки або ноги, проводяться корегуючі операції по усуненню цих деформацій. Перед цим математично розраховуються величина і кути необхідних трансплантатів.
Ось чому математику потрібно знати і лікарям.
Коли переломи лікуються за допомогою апарату зовнішньої фіксації, математично визначаються відстані між стержнями, величини компресії або дистракції . При накладанні гіпсових пов'язок необхідно правильно визначати кути фіксації кінцівок. Коли хвороби приводять до викривленя руки або ноги, проводяться корегуючі операції по усуненню цих деформацій. Перед цим математично розраховуються величина і кути необхідних трансплантатів.
Ось чому математику потрібно знати і лікарям.

Слайд #5
Тематичні питаннЯ
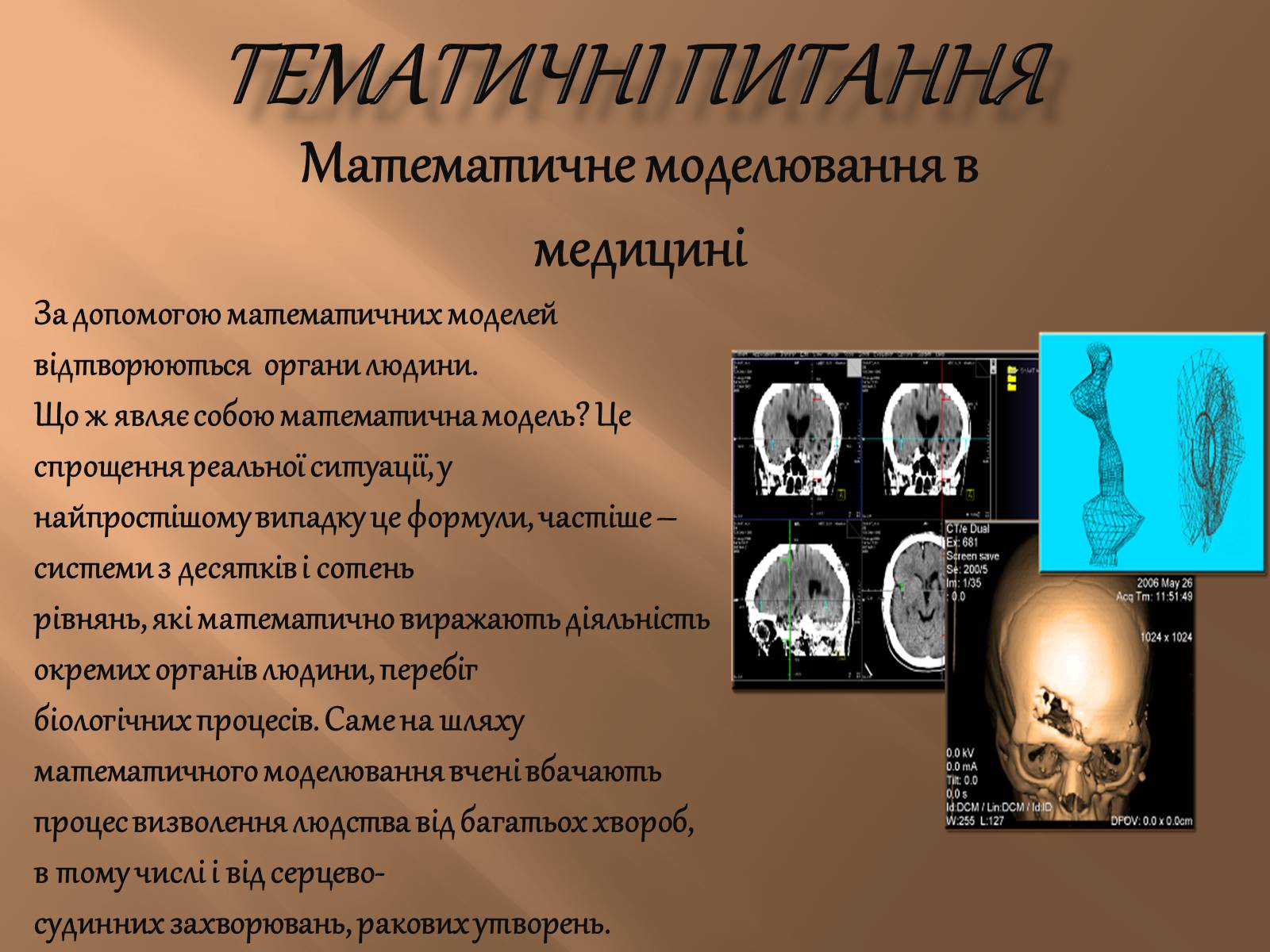
Математичне моделювання в медицині
За допомогою математичних моделей відтворюються органи людини.
Що ж являє собою математична модель? Це спрощення реальної ситуації, у
найпростішому випадку це формули, частіше – системи з десятків і сотень
рівнянь, які математично виражають діяльність окремих органів людини, перебіг
біологічних процесів. Саме на шляху математичного моделювання вчені вбачають
процес визволення людства від багатьох хвороб, в тому числі і від серцево-
судинних захворювань, ракових утворень.
Математичне моделювання в медицині
За допомогою математичних моделей відтворюються органи людини.
Що ж являє собою математична модель? Це спрощення реальної ситуації, у
найпростішому випадку це формули, частіше – системи з десятків і сотень
рівнянь, які математично виражають діяльність окремих органів людини, перебіг
біологічних процесів. Саме на шляху математичного моделювання вчені вбачають
процес визволення людства від багатьох хвороб, в тому числі і від серцево-
судинних захворювань, ракових утворень.
Слайд #6
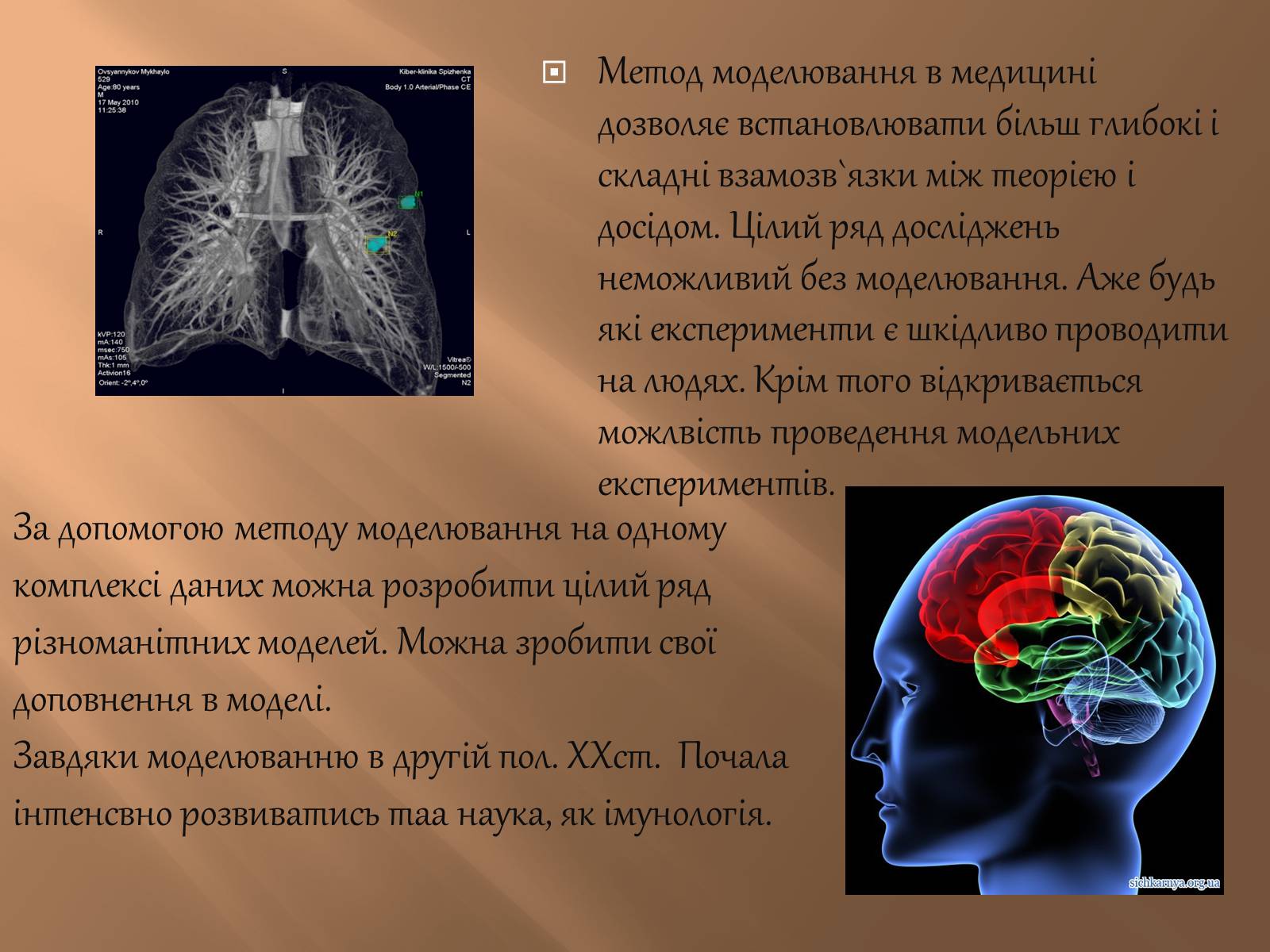
Метод моделювання в медицині дозволяє встановлювати більш глибокі і складні взамозв`язки між теорією і досідом. Цілий ряд досліджень неможливий без моделювання. Аже будь які експерименти є шкідливо проводити на людях. Крім того відкривається можлвість проведення модельних експериментів.
За допомогою методу моделювання на одному комплексі даних можна розробити цілий ряд різноманітних моделей. Можна зробити свої доповнення в моделі.
Завдяки моделюванню в другій пол. ХХст. Почала інтенсвно розвиватись таа наука, як імунологія.
За допомогою методу моделювання на одному комплексі даних можна розробити цілий ряд різноманітних моделей. Можна зробити свої доповнення в моделі.
Завдяки моделюванню в другій пол. ХХст. Почала інтенсвно розвиватись таа наука, як імунологія.
Слайд #7
Математичні формули, які відображають процес передачі захворювання
Це формули з кількома десятками інтегралів , які відображають весь процес передачі захворювання від хворої до здорової людини. За допомогою таких формул можна визначити, коли хвора людина стане найбільш небезпечною для оточуючих, коли і які ліки потрібно давати хворим тощо. Використовуючи теорію ймовірностей і методи математичної статистики, медики разом з математиками можуть враховувати, яка кількість мешканців певного регіону буде охоплена черговим спалахом грипу чи іншого інфекційного захворювання. Такий діагноз допоможе медикам заздалегідь підготувати відповідні лікувальні та профілактичні засоби.
Це формули з кількома десятками інтегралів , які відображають весь процес передачі захворювання від хворої до здорової людини. За допомогою таких формул можна визначити, коли хвора людина стане найбільш небезпечною для оточуючих, коли і які ліки потрібно давати хворим тощо. Використовуючи теорію ймовірностей і методи математичної статистики, медики разом з математиками можуть враховувати, яка кількість мешканців певного регіону буде охоплена черговим спалахом грипу чи іншого інфекційного захворювання. Такий діагноз допоможе медикам заздалегідь підготувати відповідні лікувальні та профілактичні засоби.

Слайд #8
Математична модель епідемії грипу
Вчені Київського науково-дослідного інституту епідеміології та мікробіології створили математичну модель епідемії грипу.
Детерміністична модель
Розглянемо однорідно-змішану групу, що складається із n+1 індивідуумів. Нехай в момент t в цій групі наявні x схильних до зараження індивідуумів і y джерел інфекції, тобто x+y=n+1. Припустимо що середнє число нових
випадків захворювання, що з'являються в інтервалі ∆t, будуть пропорційні як до числа y джерел інфекції. Так і до числа x схильних до заражень індивідуумів .
Вчені Київського науково-дослідного інституту епідеміології та мікробіології створили математичну модель епідемії грипу.
Детерміністична модель
Розглянемо однорідно-змішану групу, що складається із n+1 індивідуумів. Нехай в момент t в цій групі наявні x схильних до зараження індивідуумів і y джерел інфекції, тобто x+y=n+1. Припустимо що середнє число нових
випадків захворювання, що з'являються в інтервалі ∆t, будуть пропорційні як до числа y джерел інфекції. Так і до числа x схильних до заражень індивідуумів .

Слайд #9
Якщо частота контактів між членами цієї групи дорівнює β, то середнє числонових випадків захворювання,що з'являються в інтервалів ∆t, буде дорівнювати βxy∆t, тобто
∆x=-βxy∆t. Введемо змінну τ=βt
Ми передбачаємо, що зображений індивідуум стає заразним для решти
схильних індивідуумів відразу після того, як він сам заразиться, тобто що
латентний період дорівнює нулю.
Розв'язок рівняння має вигляд .
∆x=-βxy∆t. Введемо змінну τ=βt
Ми передбачаємо, що зображений індивідуум стає заразним для решти
схильних індивідуумів відразу після того, як він сам заразиться, тобто що
латентний період дорівнює нулю.
Розв'язок рівняння має вигляд .

Слайд #10
«Золотий переріз». Здоров`я і гармонія
В Інституті нормальної фізіології ім. Анохіна були піддані обстеженню кілька сотень здорових і хворих людей. У кожного вимірювали артеріальний тиск, температуру, стан легень, судин - всього більше 20 параметрів. Ці показники автоматично оброблялися на ЕОМ і відкладалися на радіусах одного кругаю. Коли сполучили ці показники однією лінією, вийшла крива – геометричне зображення стану здоров'я людини. Виявилось, чим кращий стан здоров'я, тим більше наближується крива до кола, а значення фізіологічних параметрів не виходить за межі круга.
В Інституті нормальної фізіології ім. Анохіна були піддані обстеженню кілька сотень здорових і хворих людей. У кожного вимірювали артеріальний тиск, температуру, стан легень, судин - всього більше 20 параметрів. Ці показники автоматично оброблялися на ЕОМ і відкладалися на радіусах одного кругаю. Коли сполучили ці показники однією лінією, вийшла крива – геометричне зображення стану здоров'я людини. Виявилось, чим кращий стан здоров'я, тим більше наближується крива до кола, а значення фізіологічних параметрів не виходить за межі круга.

Слайд #11
І навпаки. Коли радіуси не вміщуються в круг, час починати лікування.
Подальше дослідження показало, що співвідношення математичних значень
параметрів у тій моделі, яка може служити еталоном здоров'я, близьке до
«золотого перерізу», тієї божественної пропорції, яку вважають мірилом краси й гармонії в усіх видах мистецтв.
Золотим цей переріз називається тому, що скрізь, де він присутній, відчувається краса і гармонія. Пропорції добре розвинутого людського тіла підпорядковуються законам золотого перерізу. Перевірено, що відношення середніх значень лінійних розмірів певних частин тіла людини близьке до числа. Грецький скульптор Леохар (IV ст. до н.с.) створив статую Аполлона Бельведерського, якого в Стародавній Греції вважали ідеалом чоловічої краси.
Подальше дослідження показало, що співвідношення математичних значень
параметрів у тій моделі, яка може служити еталоном здоров'я, близьке до
«золотого перерізу», тієї божественної пропорції, яку вважають мірилом краси й гармонії в усіх видах мистецтв.
Золотим цей переріз називається тому, що скрізь, де він присутній, відчувається краса і гармонія. Пропорції добре розвинутого людського тіла підпорядковуються законам золотого перерізу. Перевірено, що відношення середніх значень лінійних розмірів певних частин тіла людини близьке до числа. Грецький скульптор Леохар (IV ст. до н.с.) створив статую Аполлона Бельведерського, якого в Стародавній Греції вважали ідеалом чоловічої краси.

Слайд #12
Аполлон Бельведерський

Слайд #13
Висновок
У даній презентації хотілося показати, що математика в медицині відіграє
важливу роль, оскільки тут присутні багато речей, які залежать від математичних обчислень.
Проте, математику недаремно називають «царицею наук», оскільки вона присутня і в астрономії, і в фізиці, і навіть у музиці….
«Ніякі людські дослідження не можна назвати справжньою наукою, якщо вони не пройшли через математичні доведення.»
Леонардо да Вінчі
У даній презентації хотілося показати, що математика в медицині відіграє
важливу роль, оскільки тут присутні багато речей, які залежать від математичних обчислень.
Проте, математику недаремно називають «царицею наук», оскільки вона присутня і в астрономії, і в фізиці, і навіть у музиці….
«Ніякі людські дослідження не можна назвати справжньою наукою, якщо вони не пройшли через математичні доведення.»
Леонардо да Вінчі
