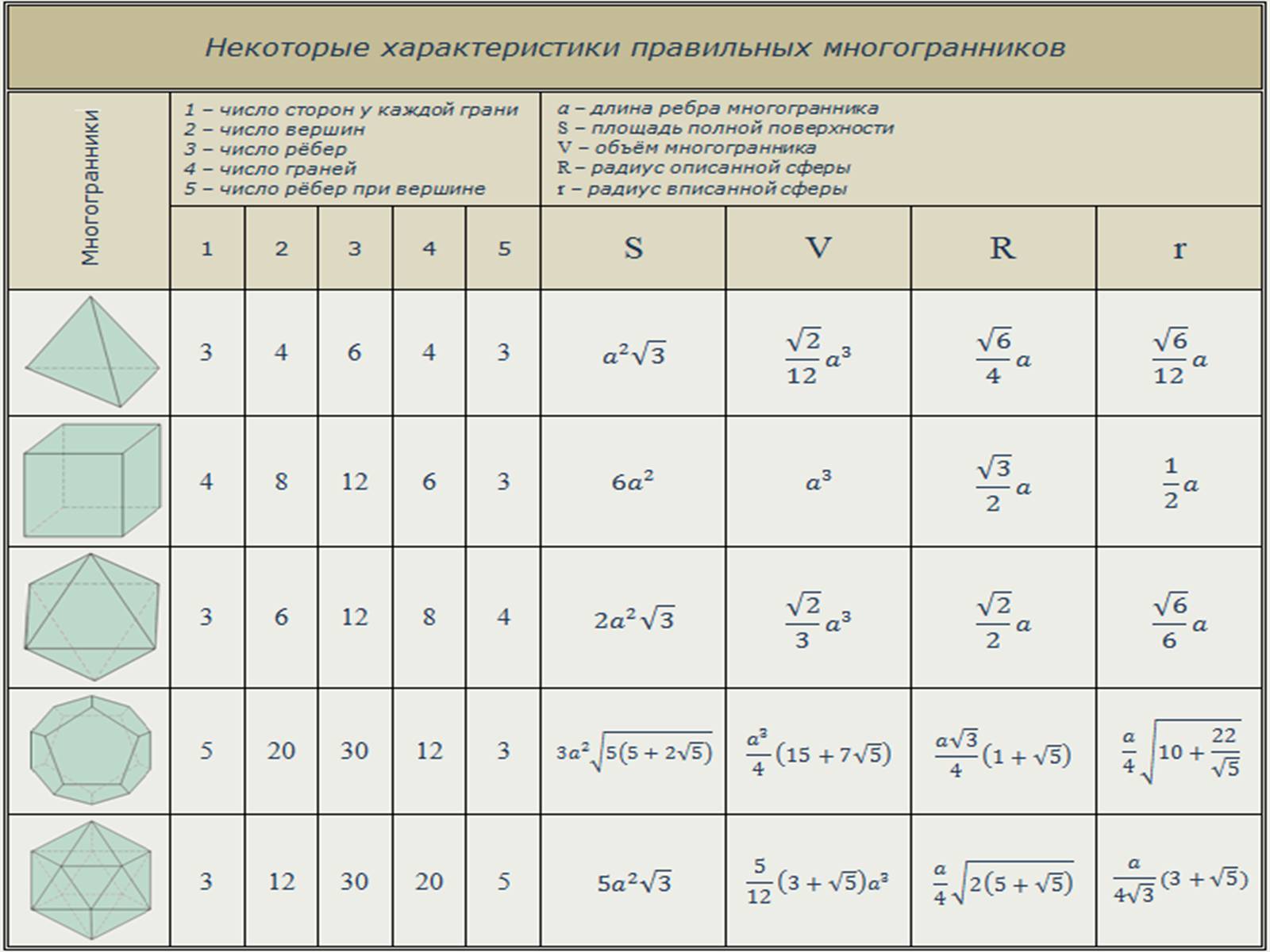
- Головна
- Готові шкільні презентації
- Презентація на тему «Многогранники» (варіант 3)
Презентація на тему «Многогранники» (варіант 3)
786
Слайд #1
КЛАС
“Многогранні кути. Многогранники”
Автор: Ананьєва Поліна
МІНІ
ПІДРУЧНИК
З ТЕМИ :
11
“Многогранні кути. Многогранники”
Автор: Ананьєва Поліна
МІНІ
ПІДРУЧНИК
З ТЕМИ :
11

Слайд #2
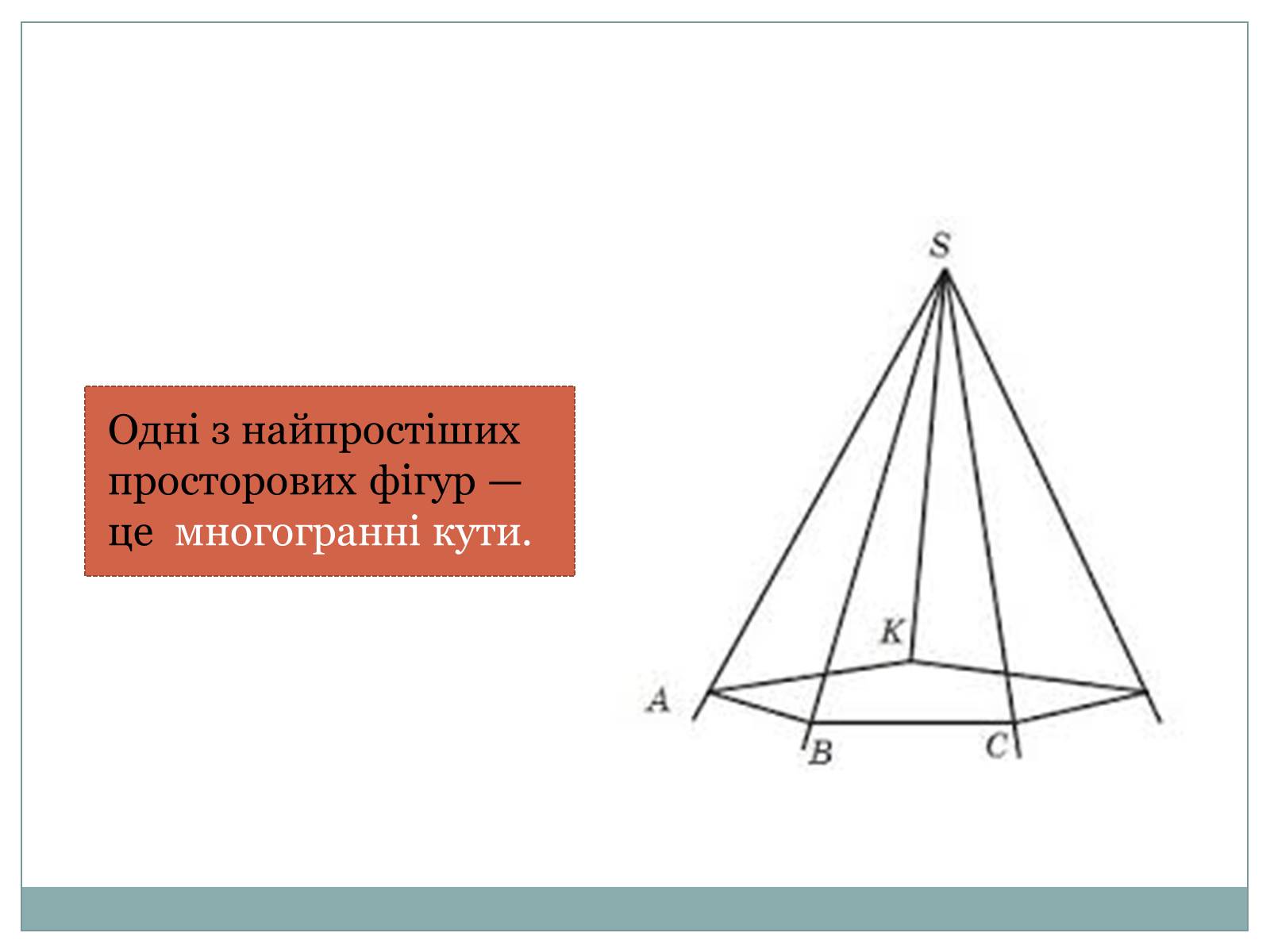
Одні з найпростіших просторових фігур — це многогранні кути.
Слайд #3
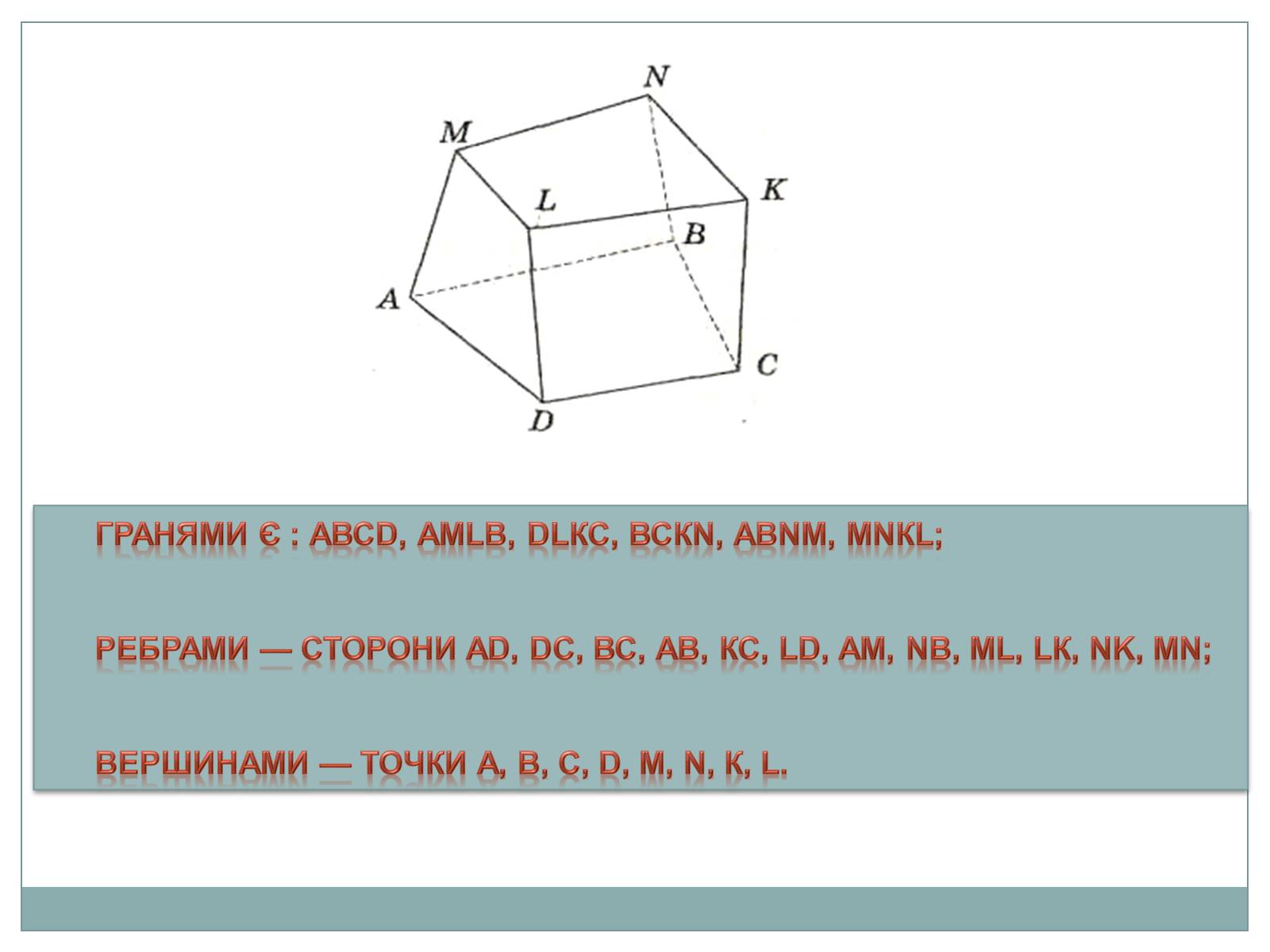
Гранями є : АВСD, АМLВ, DLКС, ВСКN, АВNМ, МNКL;
ребрами — сторони АD, DС, ВС, АВ, КС, LD, АМ, NB, МL, LК, NK, МN;
вершинами — точки А, В, С, D, М, N, К, L.
ребрами — сторони АD, DС, ВС, АВ, КС, LD, АМ, NB, МL, LК, NK, МN;
вершинами — точки А, В, С, D, М, N, К, L.
Слайд #4
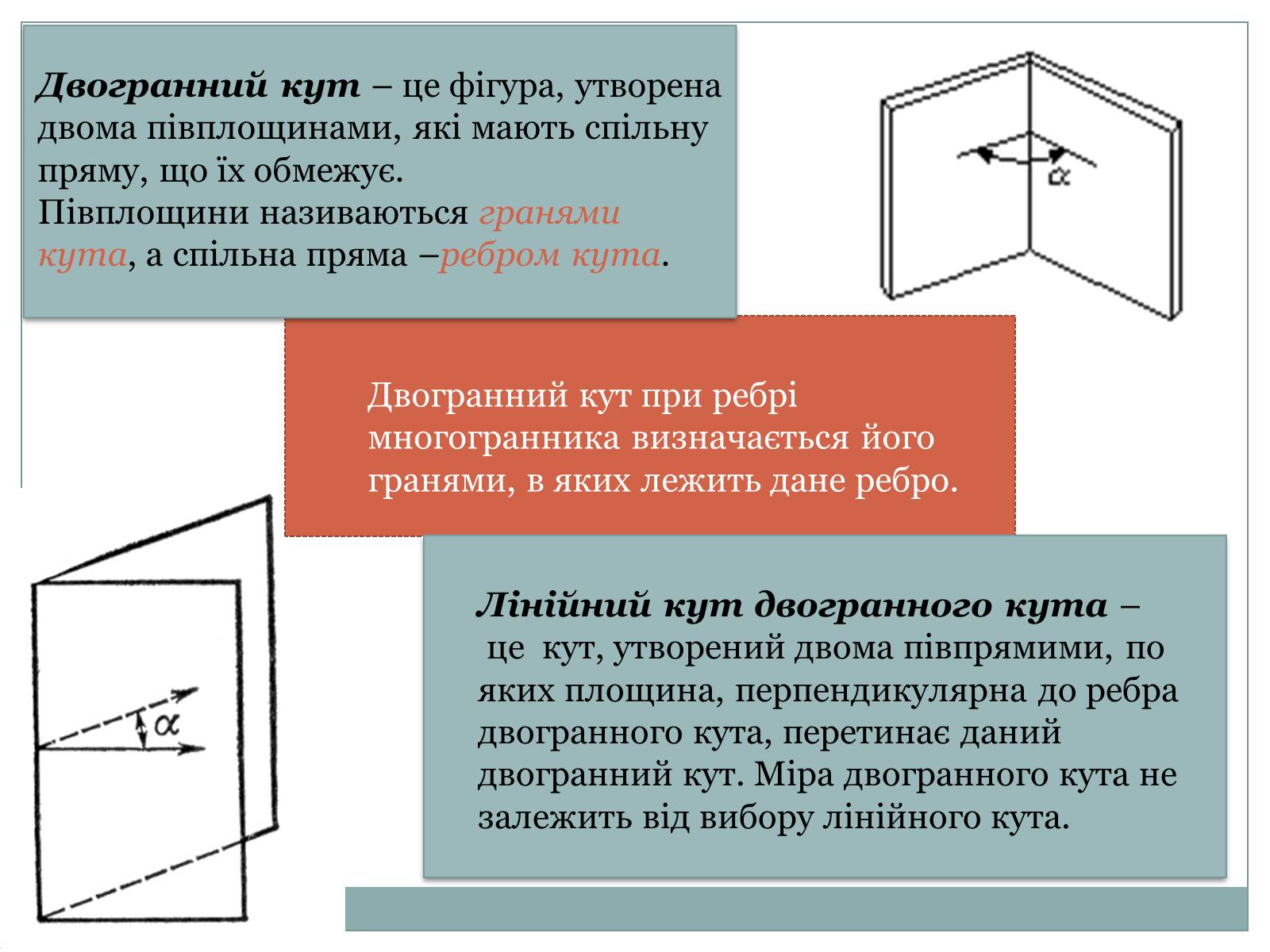
Двогранний кут – це фігура, утворена двома півплощинами, які мають спільну пряму, що їх обмежує. Півплощини називаються гранями кута, а спільна пряма –ребром кута.
Лінійний кут двогранного кута – це кут, утворений двома півпрямими, по яких площина, перпендикулярна до ребра двогранного кута, перетинає даний двогранний кут. Міра двогранного кута не залежить від вибору лінійного кута.
Двогранний кут при ребрі многогранника визначається його гранями, в яких лежить дане ребро.
Лінійний кут двогранного кута – це кут, утворений двома півпрямими, по яких площина, перпендикулярна до ребра двогранного кута, перетинає даний двогранний кут. Міра двогранного кута не залежить від вибору лінійного кута.
Двогранний кут при ребрі многогранника визначається його гранями, в яких лежить дане ребро.
Слайд #5
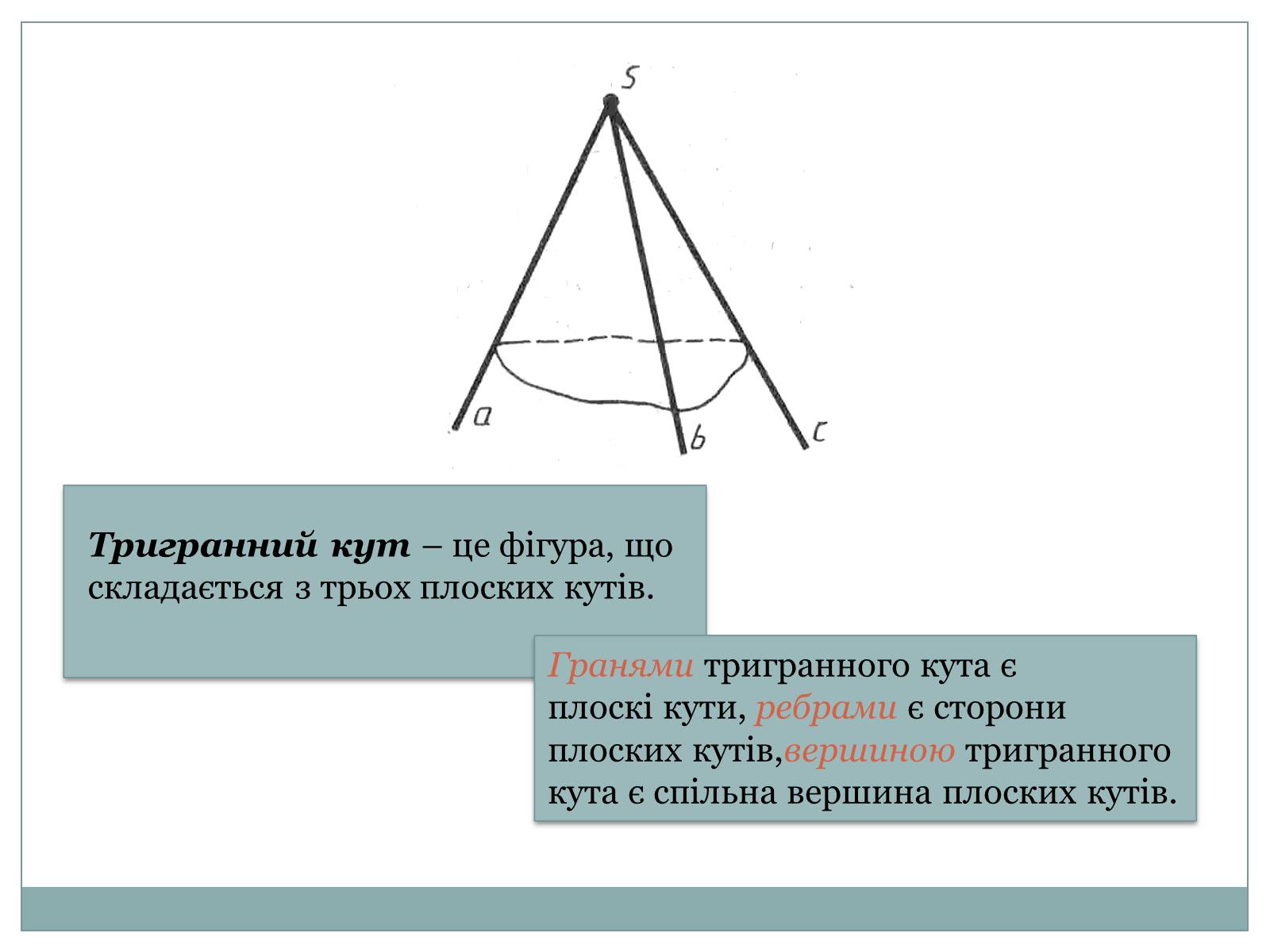
Тригранний кут – це фігура, що складається з трьох плоских кутів.
Гранями тригранного кута є плоскі кути, ребрами є сторони плоских кутів,вершиною тригранного кута є спільна вершина плоских кутів.
Гранями тригранного кута є плоскі кути, ребрами є сторони плоских кутів,вершиною тригранного кута є спільна вершина плоских кутів.
Слайд #6
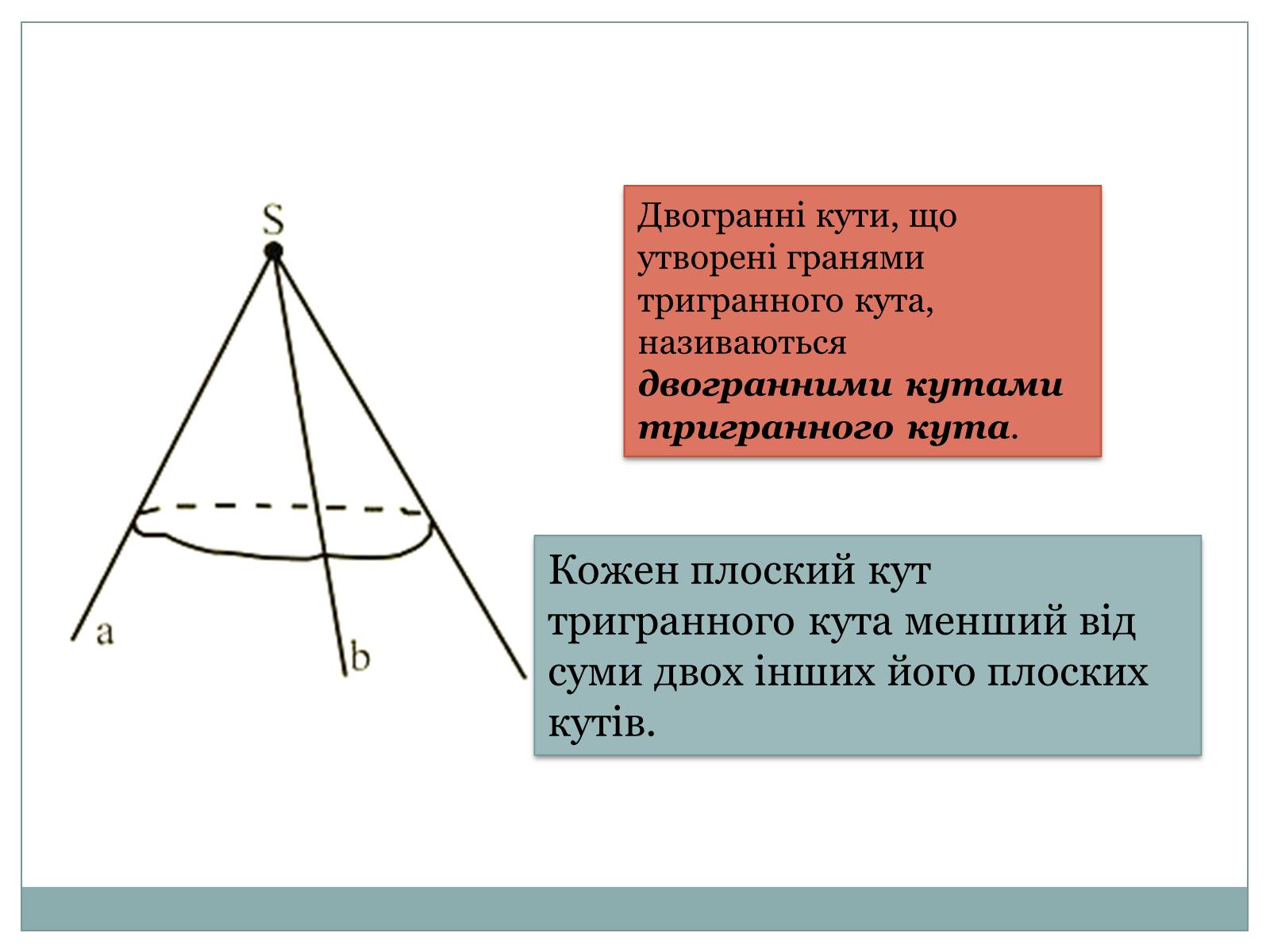
Двогранні кути, що утворені гранями тригранного кута, називаються двогранними кутами тригранного кута.
Кожен плоский кут тригранного кута менший від суми двох інших його плоских кутів.
Кожен плоский кут тригранного кута менший від суми двох інших його плоских кутів.
Слайд #7
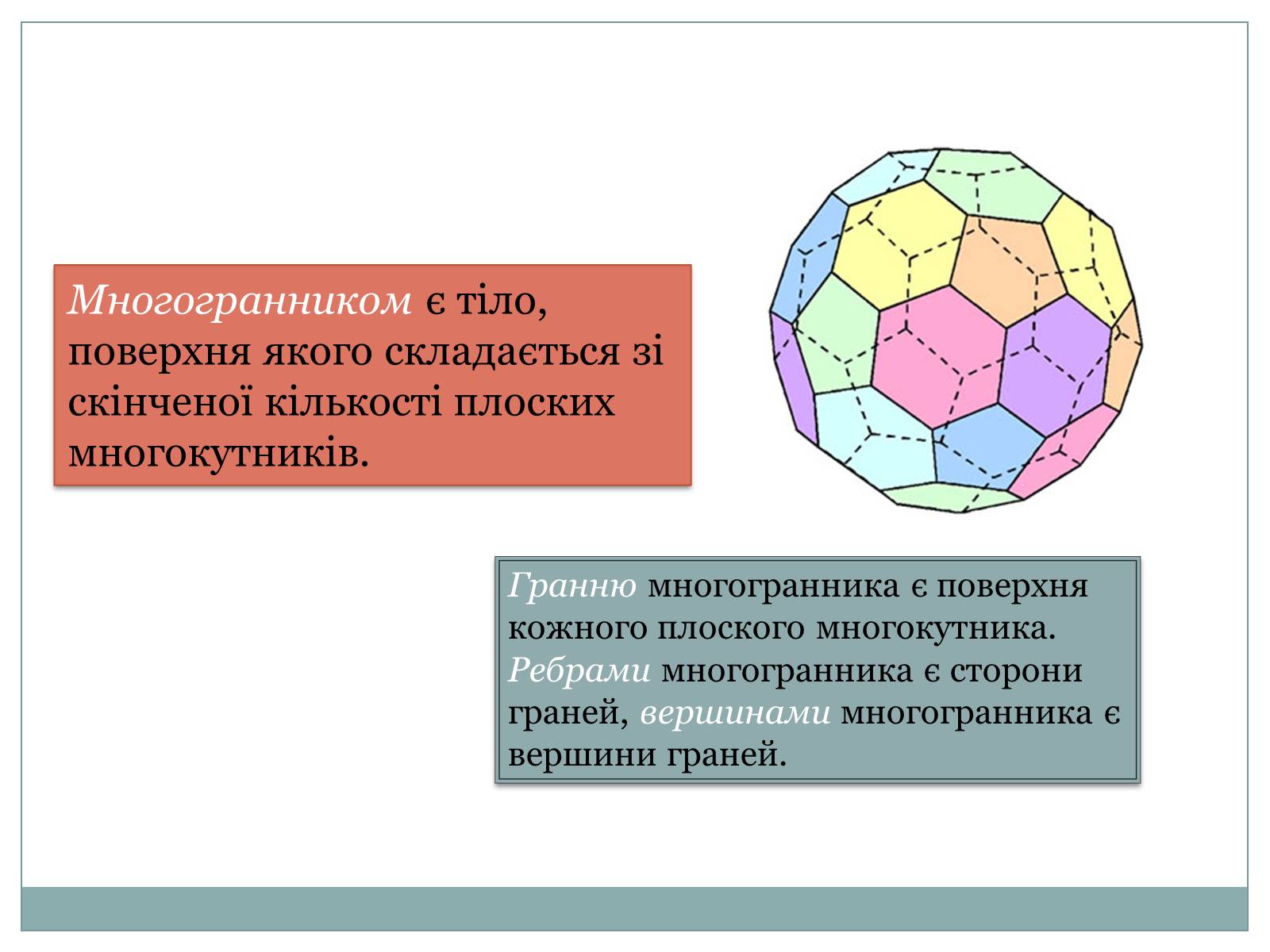
Многогранником є тіло, поверхня якого складається зі скінченої кількості плоских многокутників.
Гранню многогранника є поверхня кожного плоского многокутника.
Ребрами многогранника є сторони граней, вершинами многогранника є вершини граней.
Гранню многогранника є поверхня кожного плоского многокутника.
Ребрами многогранника є сторони граней, вершинами многогранника є вершини граней.
Слайд #8
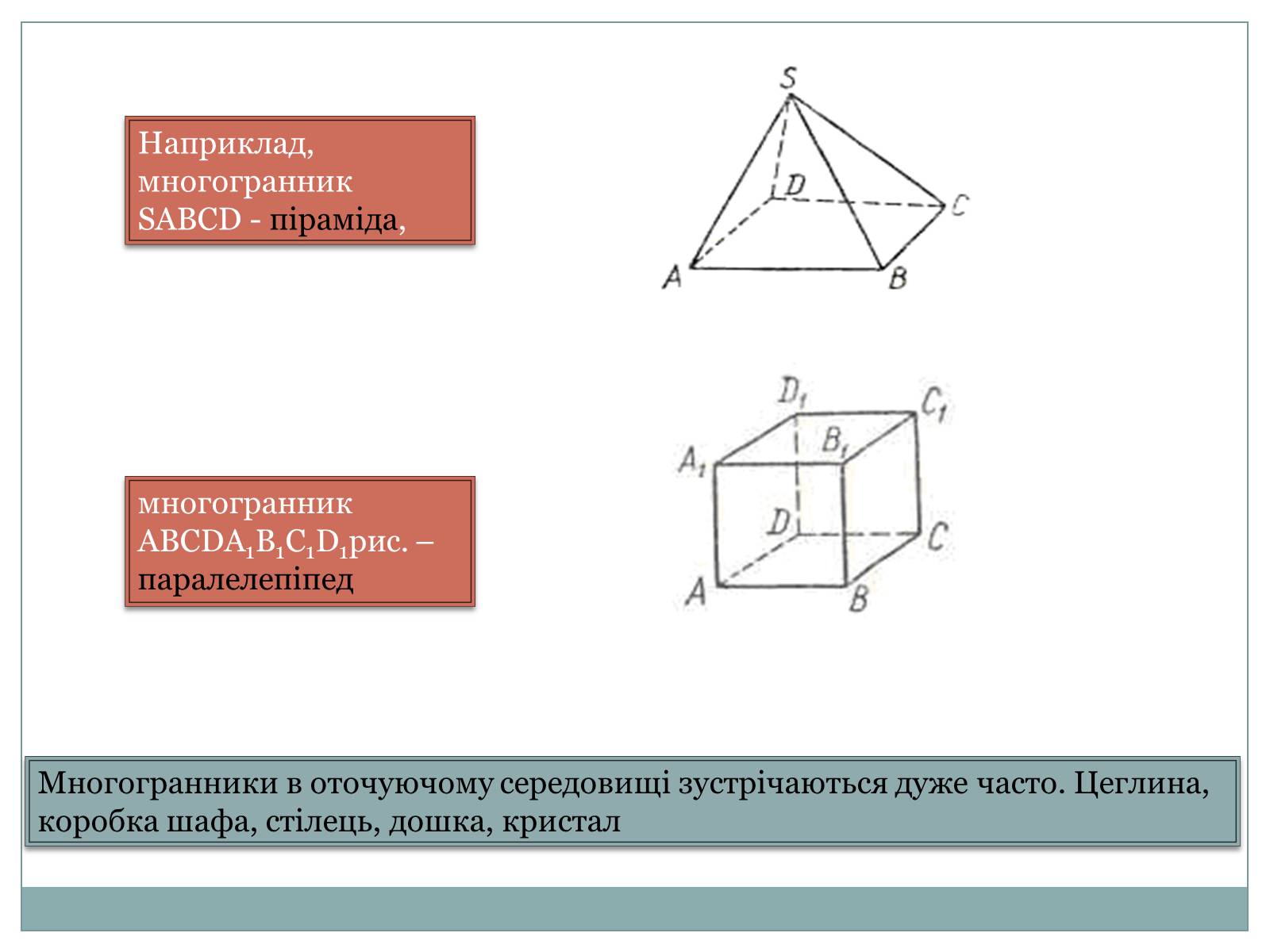
Наприклад, многогранник SАВСD - піраміда,
многогранник АВСDA1B1C1D1рис. – паралелепіпед
Многогранники в оточуючому середовищі зустрічаються дуже часто. Цеглина, коробка шафа, стілець, дошка, кристал
многогранник АВСDA1B1C1D1рис. – паралелепіпед
Многогранники в оточуючому середовищі зустрічаються дуже часто. Цеглина, коробка шафа, стілець, дошка, кристал
Слайд #9
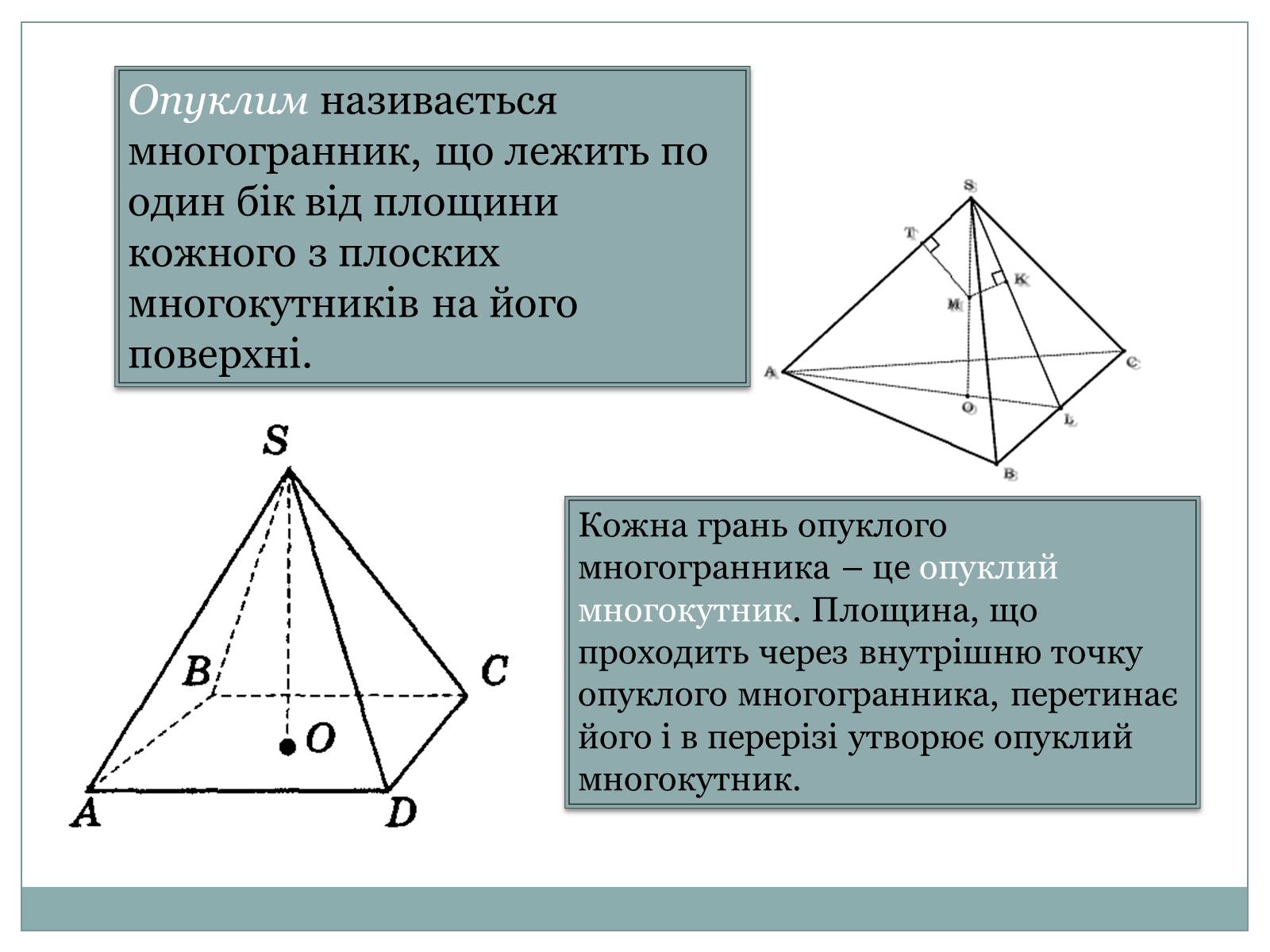
Опуклим називається многогранник, що лежить по один бік від площини кожного з плоских многокутників на його поверхні.
Кожна грань опуклого многогранника – це опуклий многокутник. Площина, що проходить через внутрішню точку опуклого многогранника, перетинає його і в перерізі утворює опуклий многокутник.
Кожна грань опуклого многогранника – це опуклий многокутник. Площина, що проходить через внутрішню точку опуклого многогранника, перетинає його і в перерізі утворює опуклий многокутник.
Слайд #10
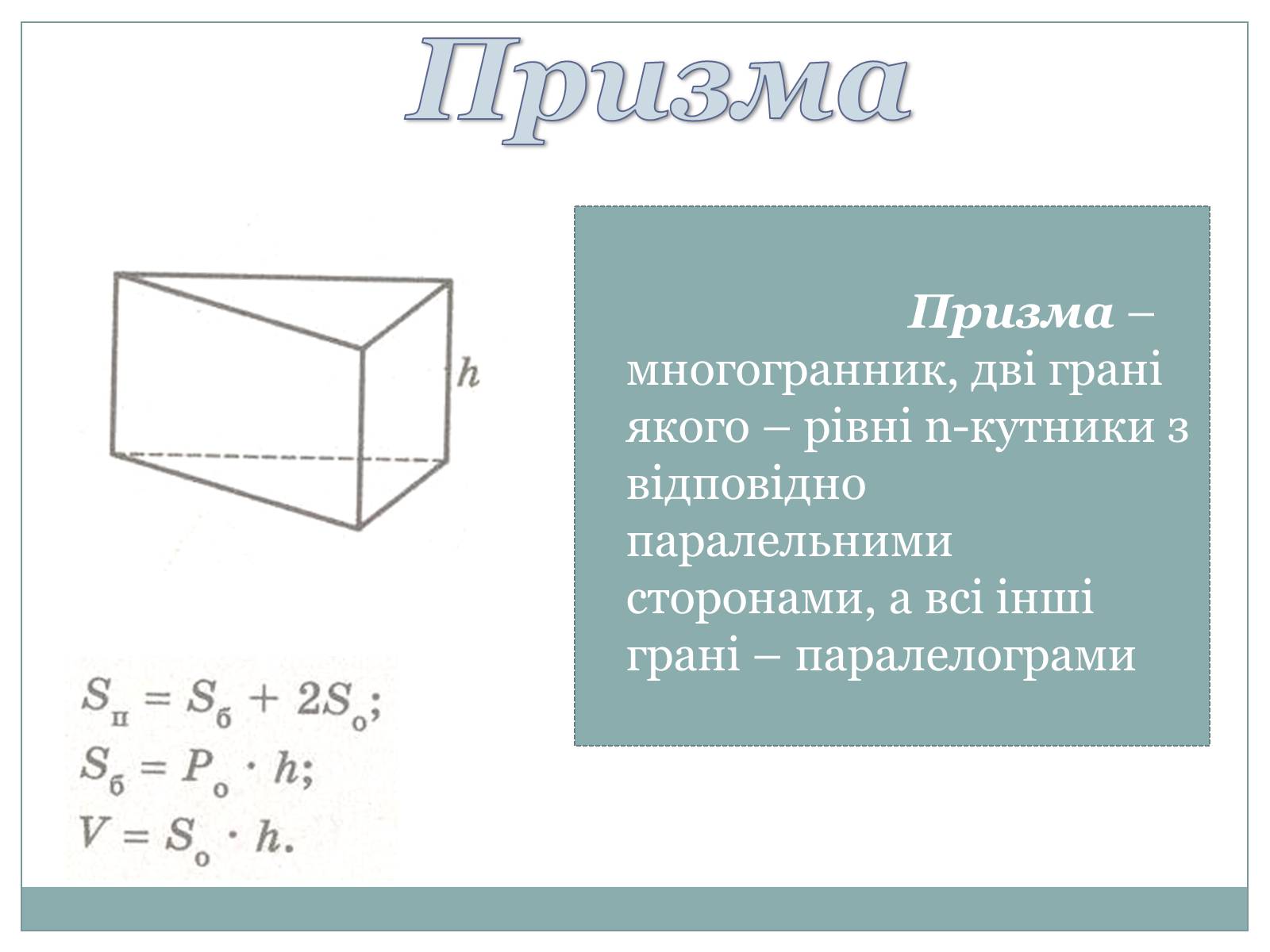
Призма – многогранник, дві грані якого – рівні n-кутники з відповідно паралельними сторонами, а всі інші грані – паралелограми
Призма
Призма
Слайд #11
Піраміда
P – вершина піраміди;
ABCD – основа піраміди;
∆PAB, ∆PBC, ∆PCD,
∆PDA – бічні грані;
PA, PB, PC, PD – бічні ребра;
AB, BC, CD, AD – ребра основи;
PO – висота, PO┴ABCD.
Піраміда – це многогранник, одна грань якого – довільний n-кутник, а всі інші – n граней трикутники, що мають спільну вершину.
P – вершина піраміди;
ABCD – основа піраміди;
∆PAB, ∆PBC, ∆PCD,
∆PDA – бічні грані;
PA, PB, PC, PD – бічні ребра;
AB, BC, CD, AD – ребра основи;
PO – висота, PO┴ABCD.
Піраміда – це многогранник, одна грань якого – довільний n-кутник, а всі інші – n граней трикутники, що мають спільну вершину.

Слайд #12
Піраміда
P – вершина піраміди;
ABCD – основа піраміди;
∆PAB, ∆PBC, ∆PCD,
∆PDA – бічні грані;
PA, PB, PC, PD – бічні ребра;
AB, BC, CD, AD – ребра основи;
PO – висота, PO┴ABCD.
Піраміда – це многогранник, одна грань якого – довільний n-кутник, а всі інші – n граней трикутники, що мають спільну вершину.
P – вершина піраміди;
ABCD – основа піраміди;
∆PAB, ∆PBC, ∆PCD,
∆PDA – бічні грані;
PA, PB, PC, PD – бічні ребра;
AB, BC, CD, AD – ребра основи;
PO – висота, PO┴ABCD.
Піраміда – це многогранник, одна грань якого – довільний n-кутник, а всі інші – n граней трикутники, що мають спільну вершину.
Слайд #13
Обчисліть площу бічної поверхні прямої призми, основою якої є паралелограм зі
сторонами 8 см і 22 см, а висота призми дорівнює 15 см.
Основою прямої призми є прямокутний трикутник із катетами 5 см і 12 см.
Висота призми дорівнює 8 см. Обчисліть площу бічної поверхні призми
У скільки разів збільшиться площа бічної поверхні правильної трикутної піраміди,
якщо сторону основи збільшити у 2 рази а апофему — в 3рази?
Основою прямої призми є чотирикутник зі сторонами 6 см, 7 см, 8 см, 9 см.
Бічне ребро призми дорівнює 10 см. Обчисліть площу бічної поверхні призми
900 см2;
800 см2;
240 см2;
240 см2;
320 см2;
640 см2;
у 6 разів;
у 9 разів;
у 17 разів;
300 см2;
400 см2;
100 см2;
сторонами 8 см і 22 см, а висота призми дорівнює 15 см.
Основою прямої призми є прямокутний трикутник із катетами 5 см і 12 см.
Висота призми дорівнює 8 см. Обчисліть площу бічної поверхні призми
У скільки разів збільшиться площа бічної поверхні правильної трикутної піраміди,
якщо сторону основи збільшити у 2 рази а апофему — в 3рази?
Основою прямої призми є чотирикутник зі сторонами 6 см, 7 см, 8 см, 9 см.
Бічне ребро призми дорівнює 10 см. Обчисліть площу бічної поверхні призми
900 см2;
800 см2;
240 см2;
240 см2;
320 см2;
640 см2;
у 6 разів;
у 9 разів;
у 17 разів;
300 см2;
400 см2;
100 см2;

Слайд #14
Площа основи правильної чотирикутної піраміди дорівнює 36 см ,
а площа її бічної поверхні - 60 см2. Знайдіть довжину апофеми цієї піраміди.
Знайдіть площу бічної поверхні правильної чотирикутної піраміди,
у якої сторона основи дорівнює 10 см, а бічне ребро — 13 см.
Знайдіть площу бічної поверхні правильної трикутної піраміди,
у якої бічне ребро дорівнює 10 см, а апофема — 6 см.
Основою прямої призми є ромб з діагоналями 10 см і 24 см.
Менша діагональ призми дорівнює 26 см.
Обчисліть площу повної поверхні призми.
;
93 см;
50 см;
20 см;
240 см2;
230 см2;
290 см2;
25 см2;
144 см2;
170 см2;
1080 см2;
100 см2;
1890 см2;
а площа її бічної поверхні - 60 см2. Знайдіть довжину апофеми цієї піраміди.
Знайдіть площу бічної поверхні правильної чотирикутної піраміди,
у якої сторона основи дорівнює 10 см, а бічне ребро — 13 см.
Знайдіть площу бічної поверхні правильної трикутної піраміди,
у якої бічне ребро дорівнює 10 см, а апофема — 6 см.
Основою прямої призми є ромб з діагоналями 10 см і 24 см.
Менша діагональ призми дорівнює 26 см.
Обчисліть площу повної поверхні призми.
;
93 см;
50 см;
20 см;
240 см2;
230 см2;
290 см2;
25 см2;
144 см2;
170 см2;
1080 см2;
100 см2;
1890 см2;

Слайд #15
Скільки граней має n-кутник?
Розв язання: З кожноъ вершини n-кутника виходить (n-3) діагоналі. Всіх вершин nвторюється 2 рази. Наприклад: А1 А2 і А3 А1. тому всіх діагоналей у
n-кутнику буде
Розв язання: З кожноъ вершини n-кутника виходить (n-3) діагоналі. Всіх вершин nвторюється 2 рази. Наприклад: А1 А2 і А3 А1. тому всіх діагоналей у
n-кутнику буде

Слайд #16
Кількість діагоналей n-кутника на 25 більша за кількість його сторін. Знайти n
Розв язання : Використовуючи формулу попереднього
прикладу , маємо
Враховуючи n>0 , отримаємо n=10
Розв язання : Використовуючи формулу попереднього
прикладу , маємо
Враховуючи n>0 , отримаємо n=10

Слайд #17
360 см2
240 см2
+3аН
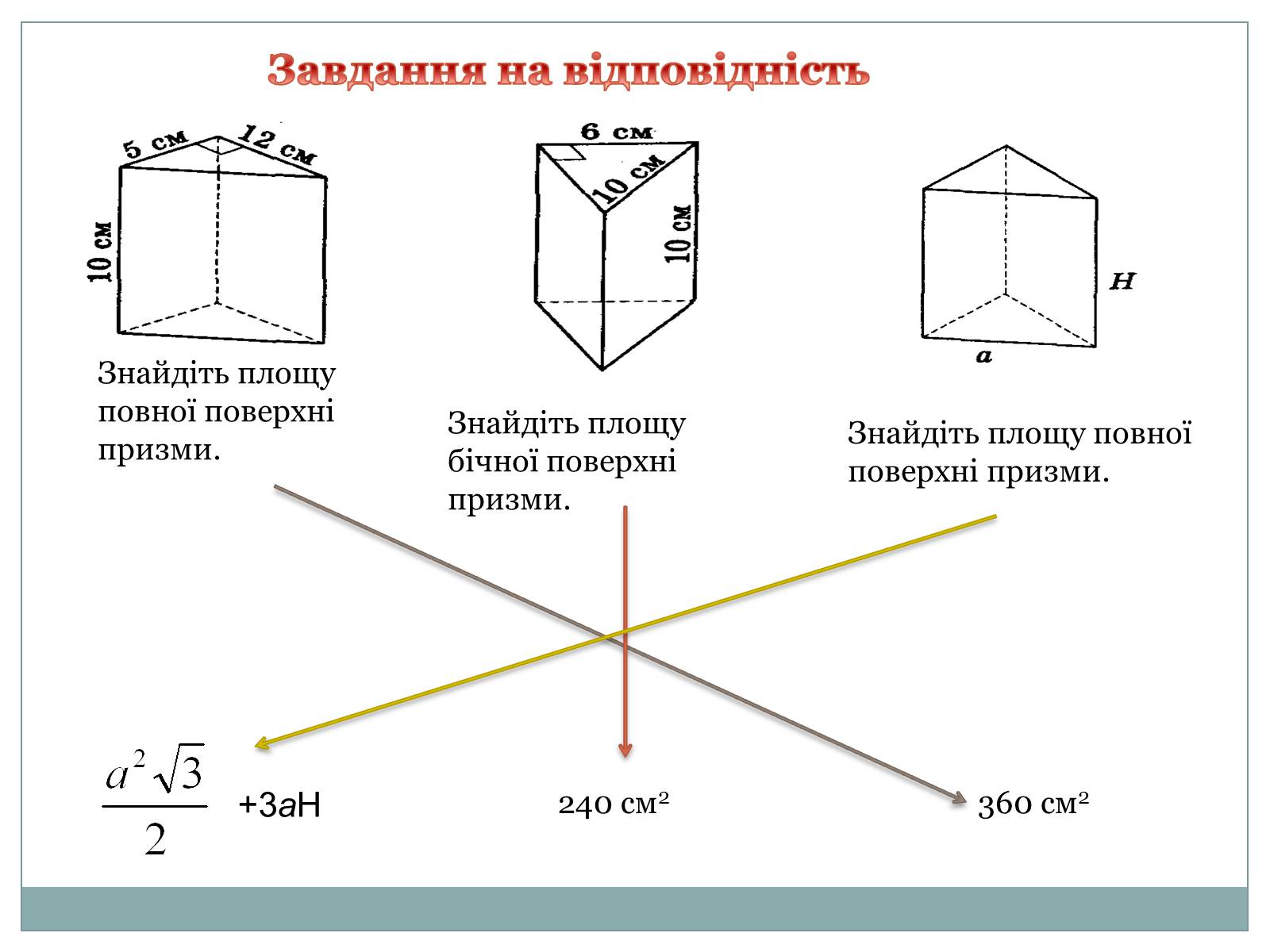
Знайдіть площу повної поверхні призми.
Знайдіть площу бічної поверхні призми.
Знайдіть площу повної поверхні призми.
Завдання на відповідність
240 см2
+3аН
Знайдіть площу повної поверхні призми.
Знайдіть площу бічної поверхні призми.
Знайдіть площу повної поверхні призми.
Завдання на відповідність
Слайд #18
4аН
l2соs
4l2·cos2
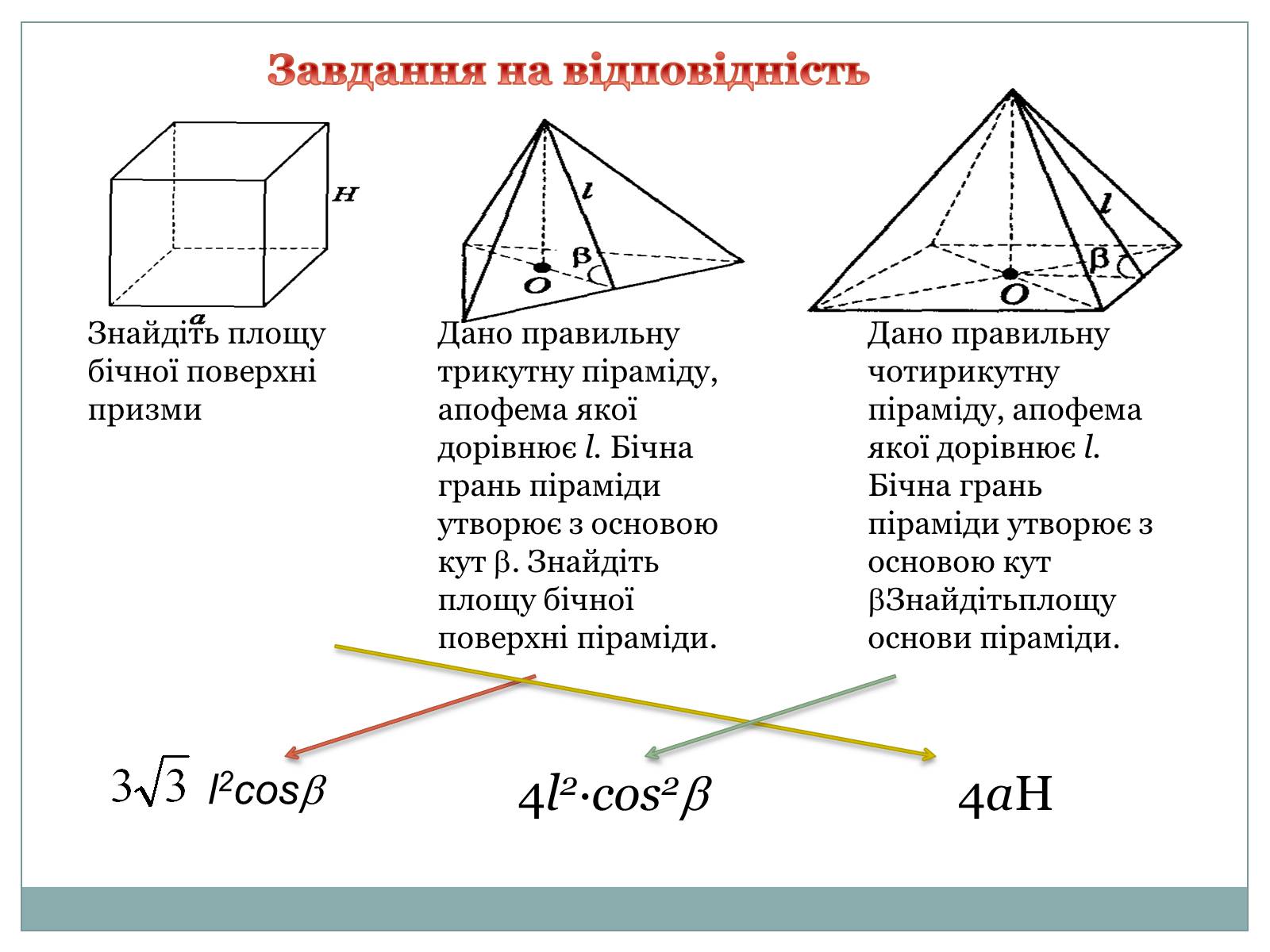
Знайдіть площу бічної поверхні призми
Дано правильну трикутну піраміду, апофема якої дорівнює l. Бічна грань піраміди утворює з основою кут . Знайдіть площу бічної поверхні піраміди.
Дано правильну чотирикутну піраміду, апофема якої дорівнює l. Бічна грань піраміди утворює з основою кут Знайдітьплощу основи піраміди.
Завдання на відповідність
l2соs
4l2·cos2
Знайдіть площу бічної поверхні призми
Дано правильну трикутну піраміду, апофема якої дорівнює l. Бічна грань піраміди утворює з основою кут . Знайдіть площу бічної поверхні піраміди.
Дано правильну чотирикутну піраміду, апофема якої дорівнює l. Бічна грань піраміди утворює з основою кут Знайдітьплощу основи піраміди.
Завдання на відповідність
Слайд #19
4аН
l2соs
4l2·cos2
Знайдіть площу бічної поверхні призми
Дано правильну трикутну піраміду, апофема якої дорівнює l. Бічна грань піраміди утворює з основою кут . Знайдіть площу бічної поверхні піраміди.
Дано правильну чотирикутну піраміду, апофема якої дорівнює l. Бічна грань піраміди утворює з основою кут Знайдітьплощу основи піраміди.
Завдання на відповідність
l2соs
4l2·cos2
Знайдіть площу бічної поверхні призми
Дано правильну трикутну піраміду, апофема якої дорівнює l. Бічна грань піраміди утворює з основою кут . Знайдіть площу бічної поверхні піраміди.
Дано правильну чотирикутну піраміду, апофема якої дорівнює l. Бічна грань піраміди утворює з основою кут Знайдітьплощу основи піраміди.
Завдання на відповідність

Слайд #20
Задача 3. У тригранному куті (abc) двогранний кут при ребрі с прямий, двогранний кут при ребрі b дорівнює κ (κ< ), а плоский кут (bc) дорівнює γ (γ < ). Знайдіть два інших плоских кути: α=ے(ab), β=ے(ac).
Дано: (abc)–тригранний кут, ےАСВ= 900, АС┴с,
АВ┴b, ےАВС= κ, ے СОВ= γ.
Знайти: ےАОВ, ے АОС.
Розв'язок.
АС┴с, АВ┴b, ےАСВ=900, то за теоремою про три
перпендикуляри СВ┴ b.
Отже ∆ОАВ, ∆ОСВ, ∆АОС і ∆АВС – прямокутні, звідси:
Відповідь: , .
Дано: (abc)–тригранний кут, ےАСВ= 900, АС┴с,
АВ┴b, ےАВС= κ, ے СОВ= γ.
Знайти: ےАОВ, ے АОС.
Розв'язок.
АС┴с, АВ┴b, ےАСВ=900, то за теоремою про три
перпендикуляри СВ┴ b.
Отже ∆ОАВ, ∆ОСВ, ∆АОС і ∆АВС – прямокутні, звідси:
Відповідь: , .

Слайд #21
Дякую за увагу !
