- Головна
- Готові шкільні презентації
- Презентація на тему «Елементи математичної логіки»
Презентація на тему «Елементи математичної логіки»
214
Слайд #1
ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ ЛОГІКИ
10 клас
10 клас

Слайд #2
«Математична логіка є логікою за предметом, математичною за методами»
Платон Порецький
(1846-1907)
(російській вчений-логік, українець за походженням)
Платон Порецький
(1846-1907)
(російській вчений-логік, українець за походженням)

Слайд #3
Що ми будемо знати ?
Висловлення та операції над ними.
Логічні закони і відношення логічного слідкування.
Предикати. Область істинності предикатів.
Операції над предикатами.
Квантори.
Теореми та їх види.
Прями й обернені теореми. Необхідні й достатні умови.
Висловлення та операції над ними.
Логічні закони і відношення логічного слідкування.
Предикати. Область істинності предикатів.
Операції над предикатами.
Квантори.
Теореми та їх види.
Прями й обернені теореми. Необхідні й достатні умови.

Слайд #4
АРІСТОТЕЛЬ(384 р.-322 р. до н.е.)
Заклав основи формальної логіки
Виклав закони логічного виведення
Розробив аксіоматичний метод
Запропонував першу формально-аксіоматичну систему логіки - силогістику
Заклав основи модальної логіки
Заклав основи формальної логіки
Виклав закони логічного виведення
Розробив аксіоматичний метод
Запропонував першу формально-аксіоматичну систему логіки - силогістику
Заклав основи модальної логіки

Слайд #5
ВИЛЬГЕЛЬМ ЛЕЙБНИЦ(1646-1716)
Розвинув ідею створення універсального логічного числення, яка далеко обігнала свій час
Склав «Азбуку думок», стислий і короткий словник символів.
Розробив ідею логічного числення.
Розмірковування позначив буквами, складні висловлювання-формулами.
В результаті вдалося змістовні міркування замінити формальними обчисленнями.
Розвинув ідею створення універсального логічного числення, яка далеко обігнала свій час
Склав «Азбуку думок», стислий і короткий словник символів.
Розробив ідею логічного числення.
Розмірковування позначив буквами, складні висловлювання-формулами.
В результаті вдалося змістовні міркування замінити формальними обчисленнями.

Слайд #6
ЗАСТОСУВАННЯ МАТЕМАТИЧНОЇ ЛОГІКИ
У теорії релейно-контактних схем і в теорії автоматів
У кібернетиці
У лінгвістиці
У економічних дослідженнях
У фізіології мозку і психології
Є основою, ядром
інтелектуальних
інформаційних систем
У теорії релейно-контактних схем і в теорії автоматів
У кібернетиці
У лінгвістиці
У економічних дослідженнях
У фізіології мозку і психології
Є основою, ядром
інтелектуальних
інформаційних систем

Слайд #7
Формальна логіка вивчає акти мислення (поняття, судження, умовиводи, доведення) з точки зору їх форми, логічної структури, абстрагуючись від конкретного змісту.
Математична логіка - наука про закони
математичного мислення.
Предметом математичної логіки є математичні теорії в цілому, які вивчаються за допомогою логіко-математичних мов.
Математична логіка вивчає способи утворення висновків з даних умов, насамперед її цікавить міркування, які використовують в математиці
Математична логіка - наука про закони
математичного мислення.
Предметом математичної логіки є математичні теорії в цілому, які вивчаються за допомогою логіко-математичних мов.
Математична логіка вивчає способи утворення висновків з даних умов, насамперед її цікавить міркування, які використовують в математиці

Слайд #8
Основні поняття логіки висловлень
Висловленням називають розповідне речення, про яке можна сказати, що воно або істинне, або хибне, але не одно й інше разом.
Розділ логіки, що вивчає висловлювання та їх властивості, називають пропозиційною логікою або логікою висловлювань (Аристотель понад 2300 років тому).
Висловленням називають розповідне речення, про яке можна сказати, що воно або істинне, або хибне, але не одно й інше разом.
Розділ логіки, що вивчає висловлювання та їх властивості, називають пропозиційною логікою або логікою висловлювань (Аристотель понад 2300 років тому).

Слайд #9
1. Сніг білий
2. Київ – столиця України
3. Х+1 = 4
4. І.Ньютон – відомий німецький математик
5. Котра година?
6. Читай уважно!
Приклади:
2. Київ – столиця України
3. Х+1 = 4
4. І.Ньютон – відомий німецький математик
5. Котра година?
6. Читай уважно!
Приклади:

Слайд #10
У математичній логіці висловлення вважають своєрідною змінною, яка може набувати лише одного з двох значень: «істина» або «хибність», такі змінні називають логічними змінними.
А= {Київ – столиця України}
В= {І.Ньютон – відомий німецький математик}
Якщо висловлення істинне то його можна позначати: Т, I, або 1.
Якщо висловлення хибне то його позначають: Х, F або 0.
А= {Київ – столиця України}
В= {І.Ньютон – відомий німецький математик}
Якщо висловлення істинне то його можна позначати: Т, I, або 1.
Якщо висловлення хибне то його позначають: Х, F або 0.

Слайд #11
Якщо задано деяку множину висловлень, то можна розглядати функцію f, областю визначення якої є ця множина, а областю значень – двоелементна множина {0,1}. Таку функцію f будемо називати функцією істинності.
Наприклад:
якщо А={16 ділиться на 2}, то f(А)=1.
Наприклад:
якщо А={16 ділиться на 2}, то f(А)=1.

Слайд #12
Логічні операції над висловленнями
Заперечення
Запереченням висловлення А називають висловлення, яке є істинним, коли висловлення А хибне, і є хибним, коли висловлення А істинне.
Позначається заперечення:Ā ,¬ А, ~А.
Читається:«не А», «неправильно, що А».
Заперечення
Запереченням висловлення А називають висловлення, яке є істинним, коли висловлення А хибне, і є хибним, коли висловлення А істинне.
Позначається заперечення:Ā ,¬ А, ~А.
Читається:«не А», «неправильно, що А».

Слайд #13
А
Ā
1
1
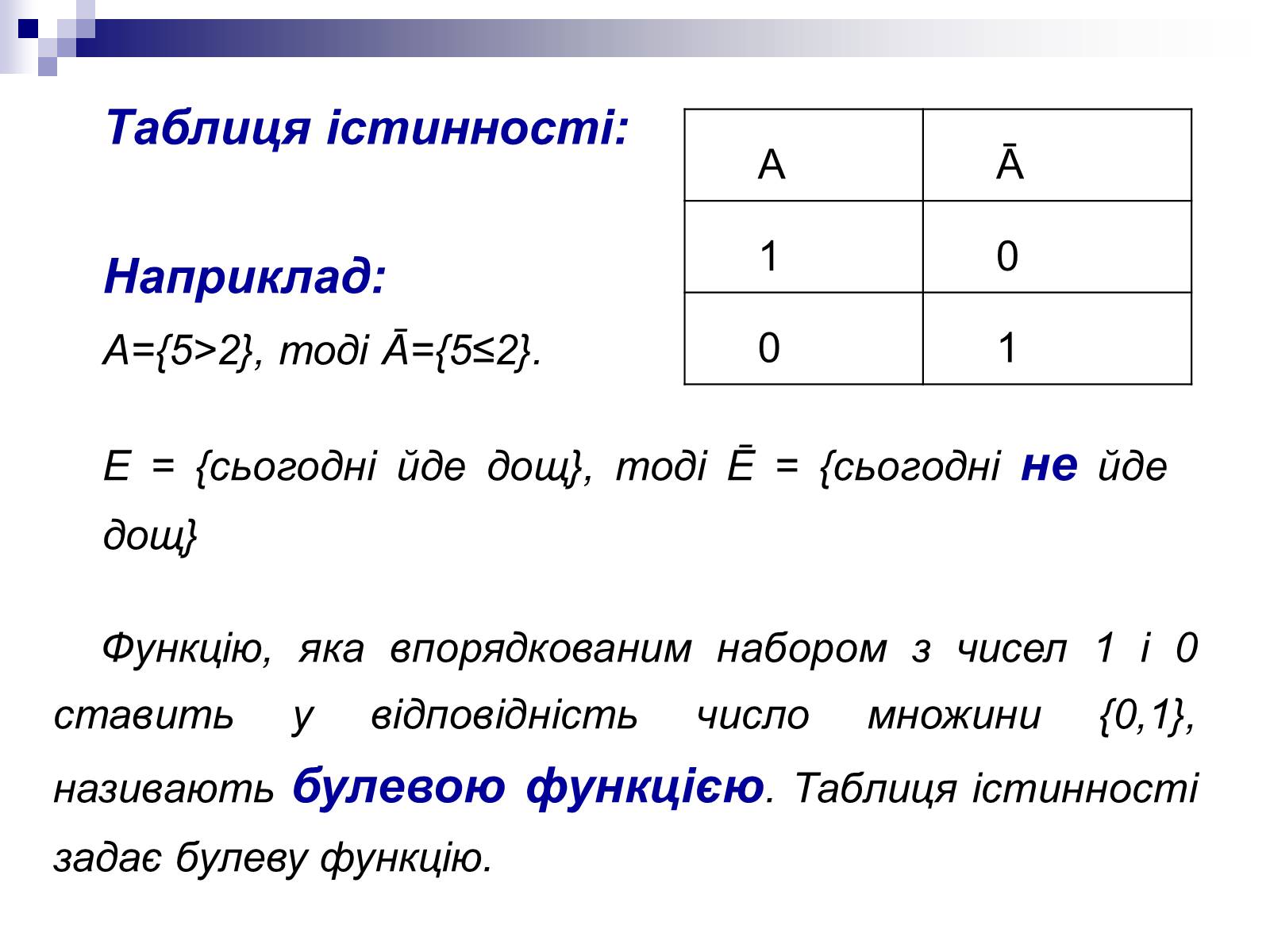
Наприклад:
А={5>2}, тоді Ā={5≤2}.
Е = {сьогодні йде дощ}, тоді Ē = {сьогодні не йде дощ}
Таблиця істинності:
Функцію, яка впорядкованим набором з чисел 1 і 0 ставить у відповідність число множини {0,1}, називають булевою функцією. Таблиця істинності задає булеву функцію.
Ā
1
1
Наприклад:
А={5>2}, тоді Ā={5≤2}.
Е = {сьогодні йде дощ}, тоді Ē = {сьогодні не йде дощ}
Таблиця істинності:
Функцію, яка впорядкованим набором з чисел 1 і 0 ставить у відповідність число множини {0,1}, називають булевою функцією. Таблиця істинності задає булеву функцію.
Слайд #14
Кон'юнкція
Кон'юнкцією (або логічним добутком) двох висловлень А і В називають висловлення, яке є істинним, коли кожне з висловлень А і В істинне, і є хибним, коли хоча б одне з них хибне.
Позначається кон'юнкція: А ^ В, А& В.
Читається:«А і В», «А кон'юнкція В».
Кон'юнкцією (або логічним добутком) двох висловлень А і В називають висловлення, яке є істинним, коли кожне з висловлень А і В істинне, і є хибним, коли хоча б одне з них хибне.
Позначається кон'юнкція: А ^ В, А& В.
Читається:«А і В», «А кон'юнкція В».

Слайд #15
А
В
А ^ В
1
1
1
1
1
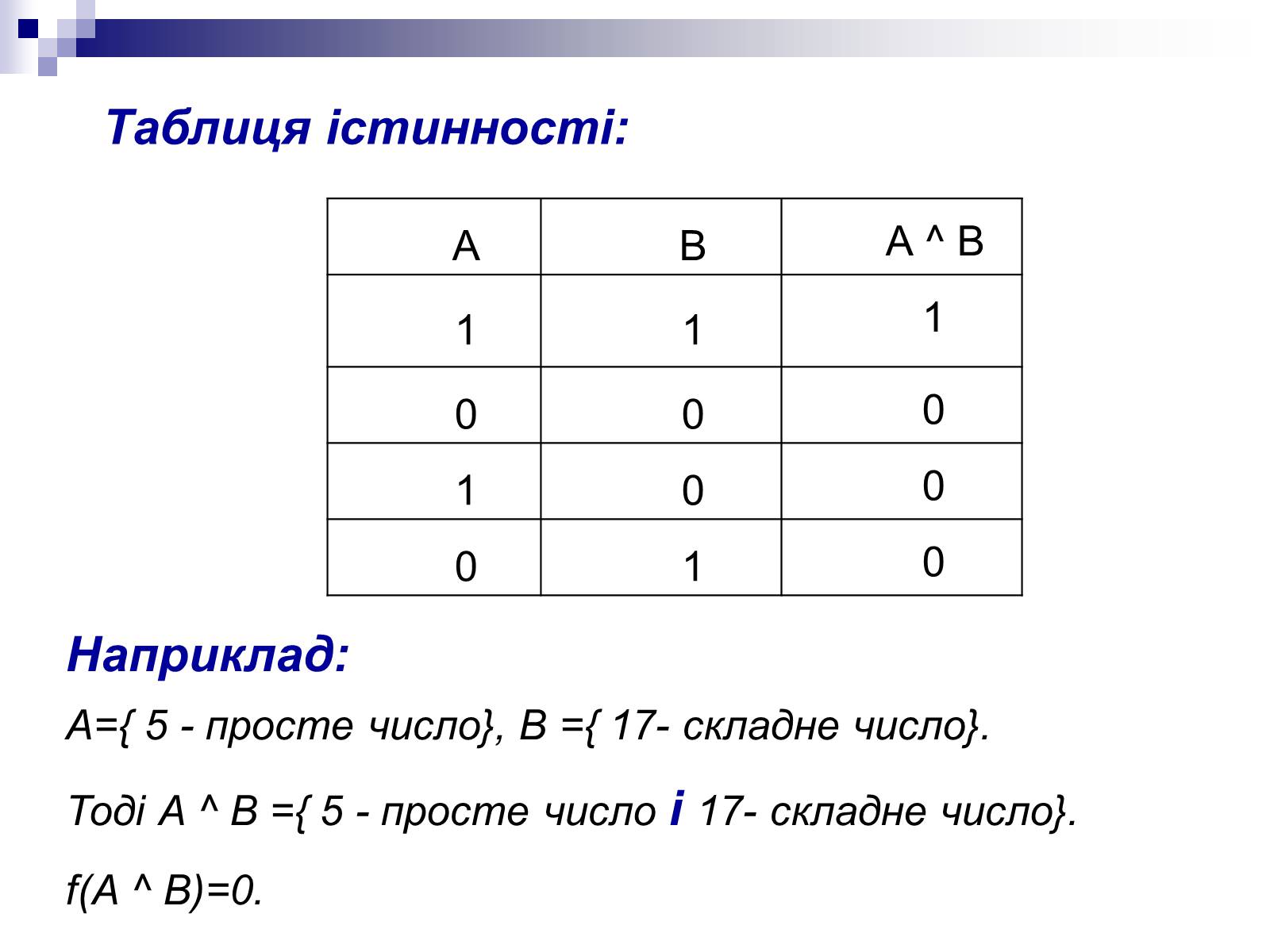
Наприклад:
А={ 5 - просте число}, В ={ 17- складне число}.
Тоді А ^ В ={ 5 - просте число і 17- складне число}.
f(А ^ В)=0.
Таблиця істинності:
В
А ^ В
1
1
1
1
1
Наприклад:
А={ 5 - просте число}, В ={ 17- складне число}.
Тоді А ^ В ={ 5 - просте число і 17- складне число}.
f(А ^ В)=0.
Таблиця істинності:
Слайд #16
Диз'юнкція
Диз'юнкцією (або логічною сумою) двох висловлень А і В називають висловлення, яке є істинним, коли хоча б одне з висловлень А або В істинне, і є хибним, коли обидва хибні.
Позначається диз'юнкція: АvВ.
Читається:«А або В», «А диз'юнкція В».
Диз'юнкцією (або логічною сумою) двох висловлень А і В називають висловлення, яке є істинним, коли хоча б одне з висловлень А або В істинне, і є хибним, коли обидва хибні.
Позначається диз'юнкція: АvВ.
Читається:«А або В», «А диз'юнкція В».

Слайд #17
А
В
А v В
1
1
1
1
1
1
1
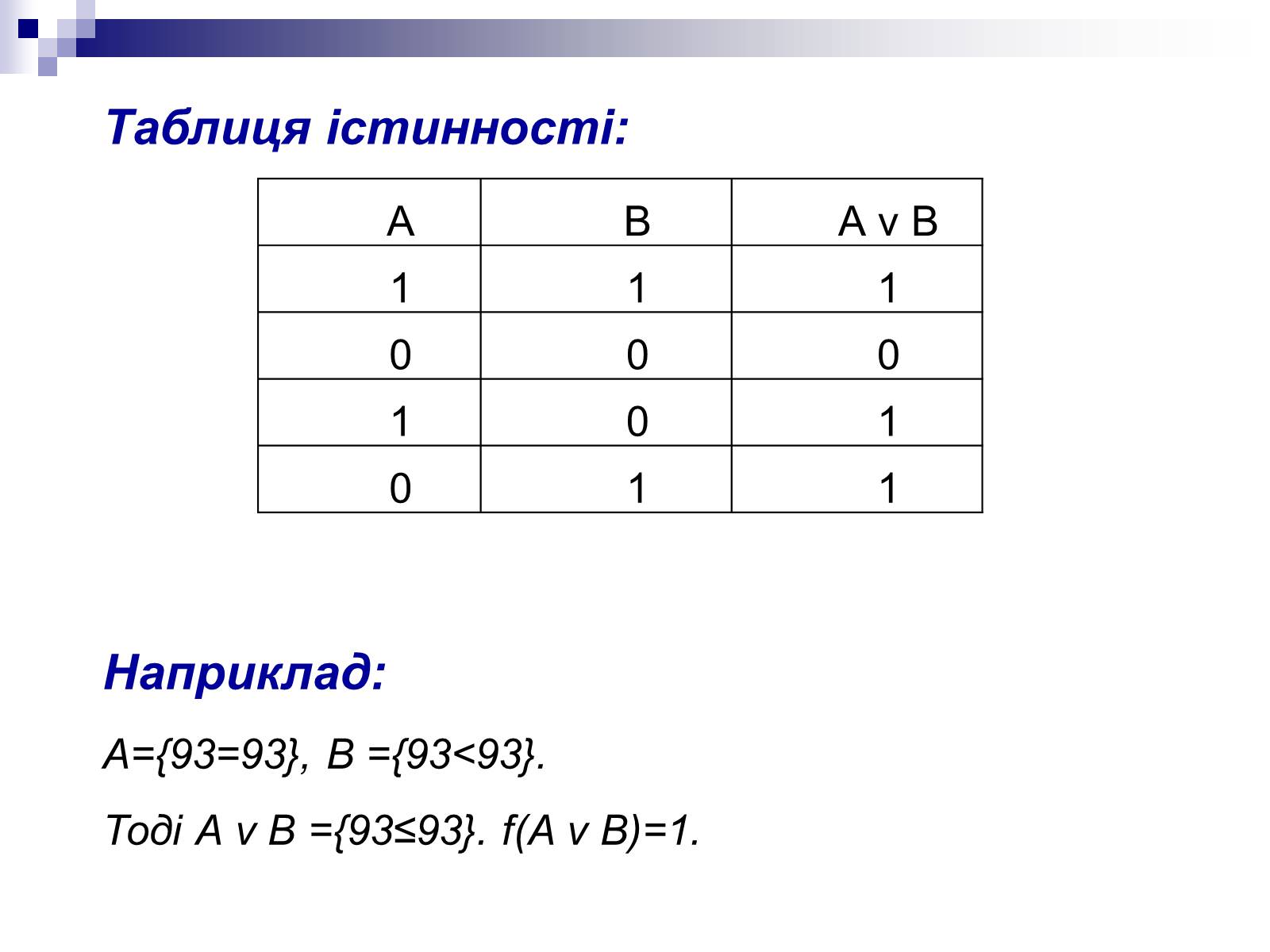
Наприклад:
А={93=93}, В ={93<93}.
Тоді А v В ={93≤93}. f(А v В)=1.
Таблиця істинності:
В
А v В
1
1
1
1
1
1
1
Наприклад:
А={93=93}, В ={93<93}.
Тоді А v В ={93≤93}. f(А v В)=1.
Таблиця істинності:
Слайд #18
Імплікація
Імплікацією (або логічним слідуванням) двох висловлень А і В називають таке висловлення А В, яке є хибним тоді і тільки тоді, коли А - істинне, а В - хибне.
Позначається імплікація: А В, А В, А В, А > В.
Читається: «якщо А, то В», «А імплікує В», «з А випливає В».
Висловлення А – називається умовою імплікації, В - наслідком імплікації.
Імплікацією (або логічним слідуванням) двох висловлень А і В називають таке висловлення А В, яке є хибним тоді і тільки тоді, коли А - істинне, а В - хибне.
Позначається імплікація: А В, А В, А В, А > В.
Читається: «якщо А, то В», «А імплікує В», «з А випливає В».
Висловлення А – називається умовою імплікації, В - наслідком імплікації.

Слайд #19
Наприклад:
А={36 ділиться на 24}, В ={36>24}. Тоді f(А В) =1,
а f(В А)=0
А
В
А В
1
1
1
1
1
1
1
Таблиця істинності:
А={36 ділиться на 24}, В ={36>24}. Тоді f(А В) =1,
а f(В А)=0
А
В
А В
1
1
1
1
1
1
1
Таблиця істинності:

Слайд #20
Еквіваленція
Еквіваленцією двох висловлень А і В називається таке висловлення, яке істинне тоді і тільки тоді, коли обидва компоненти А і В однозначно істинні або однозначно хибні.
Позначається еквіваленція: А В, А~В.
Читається: « А еквівалентне В», «А тоді і тільки тоді, коли В».
Еквіваленцією двох висловлень А і В називається таке висловлення, яке істинне тоді і тільки тоді, коли обидва компоненти А і В однозначно істинні або однозначно хибні.
Позначається еквіваленція: А В, А~В.
Читається: « А еквівалентне В», «А тоді і тільки тоді, коли В».

Слайд #21
Наприклад:
А={585 ділиться на 9}, В ={сума цифр числа 585 ділиться на 9}. Тоді f(А В)=1.
А
В
А В
1
1
1
1
1
1
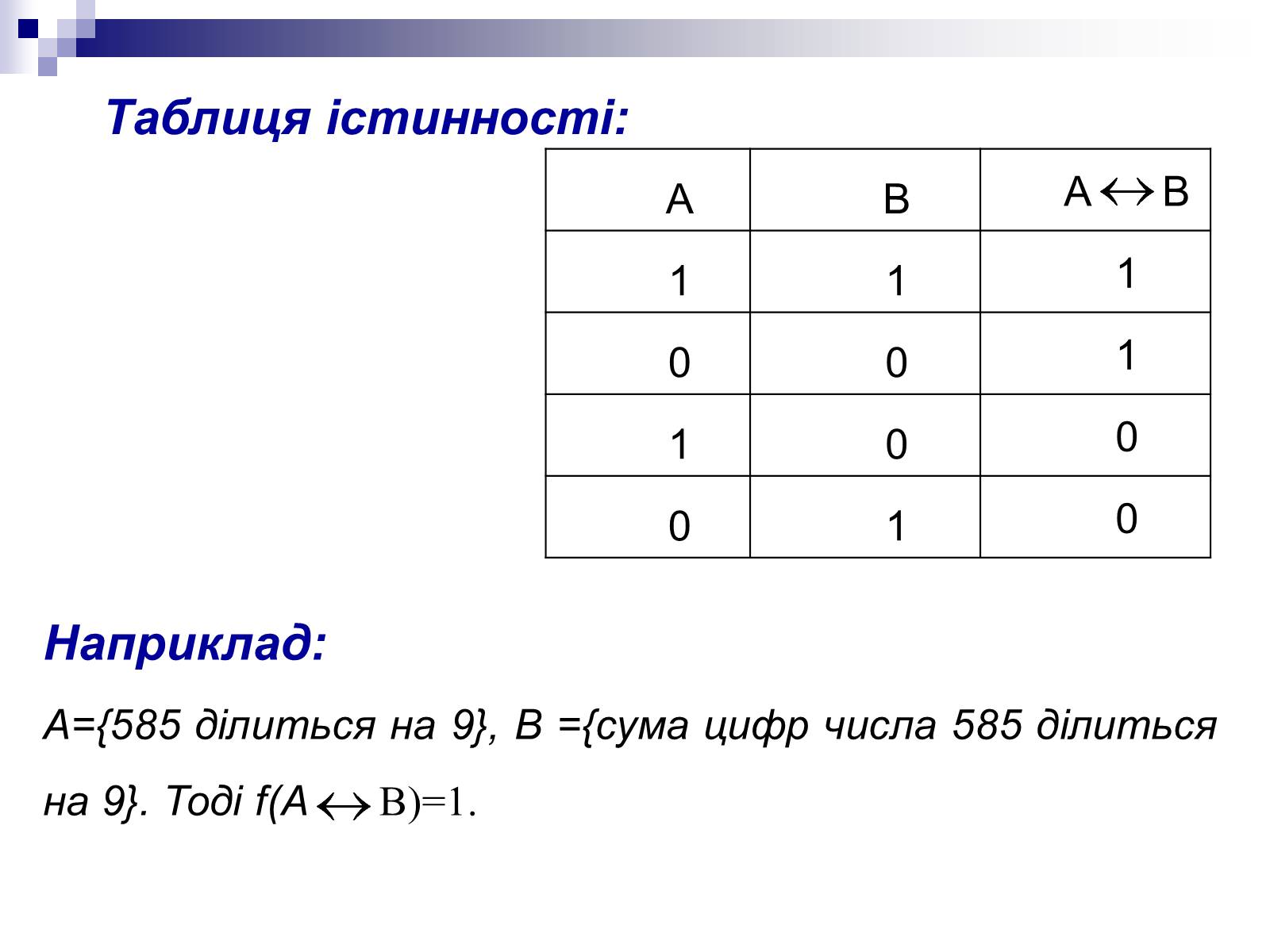
Таблиця істинності:
А={585 ділиться на 9}, В ={сума цифр числа 585 ділиться на 9}. Тоді f(А В)=1.
А
В
А В
1
1
1
1
1
1
Таблиця істинності:
Слайд #22
ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ ЛОГІКИ
2 урок
2 урок

Слайд #23
«Недостатньо мати гарний розум. Головне правильно його використовувати.»
Рене Декарт
Рене Декарт

Слайд #24
Домашнє завдання:
Опрацювати записи конспекту.
Вивчити основні означення.
Виконати завдання:
№1: Навести кілька прикладів висловлень та їх заперечень.
№2: Навести кілька прикладів диз'юнкції двох висловлень.
№3: Навести кілька прикладів кон'юнкції двох висловлень.
№4: Навести кілька прикладів імплікації двох висловлень.
№5:Навести кілька прикладів еквіваленції двох висловлень.
Опрацювати записи конспекту.
Вивчити основні означення.
Виконати завдання:
№1: Навести кілька прикладів висловлень та їх заперечень.
№2: Навести кілька прикладів диз'юнкції двох висловлень.
№3: Навести кілька прикладів кон'юнкції двох висловлень.
№4: Навести кілька прикладів імплікації двох висловлень.
№5:Навести кілька прикладів еквіваленції двох висловлень.

Слайд #25
Усне розв'язування завдань:
1. Наведіть кілька прикладів речень, які:
а) будуть висловленнями;
б) не будуть висловленнями.
2. Наведіть кілька прикладів істинних і хибних висловлень.
1. Наведіть кілька прикладів речень, які:
а) будуть висловленнями;
б) не будуть висловленнями.
2. Наведіть кілька прикладів істинних і хибних висловлень.

Слайд #26
3. Які з наведених нижче висловлень істинні, а які – хибні:
а) {вирази і тотожно рівні»};
б) {сума ділиться на 200};
в) {різниця ділиться на 7};
г) {рівняння 50х =х не має коренів};
д) {рівність 18:11=7:4 є пропорцією};
е) {якщо многокутники мають рівні периметри, то їх площі також рівні};
є) {якщо трапеція вписана в коло, то вона рівнобедрена}.
а) {вирази і тотожно рівні»};
б) {сума ділиться на 200};
в) {різниця ділиться на 7};
г) {рівняння 50х =х не має коренів};
д) {рівність 18:11=7:4 є пропорцією};
е) {якщо многокутники мають рівні периметри, то їх площі також рівні};
є) {якщо трапеція вписана в коло, то вона рівнобедрена}.

Слайд #27
1. Які з наведених виразів є висловленнями? Якщо вираз є висловленням, то вказати, яким саме — істинним чи хибним.
а) 15 кратне 3, але не кратне 4.
б) Кожне дійсне число задовольняє нерівністьх20.
в) Число 168 кратне 9.
г) Ця задача легка.
д) Існує найбільше просте число.
е) Рівняння x2+ 7x+ 1= 0 має хоч один дійсний корінь.
є) Розв'язати рівняння x2 + 7x + 1= 0.
Самостійна робота:
а) 15 кратне 3, але не кратне 4.
б) Кожне дійсне число задовольняє нерівністьх20.
в) Число 168 кратне 9.
г) Ця задача легка.
д) Існує найбільше просте число.
е) Рівняння x2+ 7x+ 1= 0 має хоч один дійсний корінь.
є) Розв'язати рівняння x2 + 7x + 1= 0.
Самостійна робота:

Слайд #28
ж) Кожне парне число, більше за 2, є сумою двох простих чисел.
з) Розкрийте підручник на сторінці 23.
к) Вчитель сказав: «Розкрийте підручник на сторінці 23».
л) Всі дійсні числа задовольняють нерівність х2 9.
м) 1 є просте число.
н) Хай живе математика!
о) Якщо 3< 2, то 32 <22.
п) На дошці написано лише одне речення: «Те, що написано на дошці,- неправда».
з) Розкрийте підручник на сторінці 23.
к) Вчитель сказав: «Розкрийте підручник на сторінці 23».
л) Всі дійсні числа задовольняють нерівність х2 9.
м) 1 є просте число.
н) Хай живе математика!
о) Якщо 3< 2, то 32 <22.
п) На дошці написано лише одне речення: «Те, що написано на дошці,- неправда».

Слайд #29
2. Занумерувати послідовність виконання операцій у формулах:
а) AB(AC)BC;
б) (A((BC)D))(CB)CA.
3. Порівняти послідовність виконання логічних операцій у формулах:
а) (A(BC))((AB)(AC)) і
(A(BC)(AB))(AC);
б) (ABC)(BC) і (BC(BC).
а) AB(AC)BC;
б) (A((BC)D))(CB)CA.
3. Порівняти послідовність виконання логічних операцій у формулах:
а) (A(BC))((AB)(AC)) і
(A(BC)(AB))(AC);
б) (ABC)(BC) і (BC(BC).

Слайд #30
ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ ЛОГІКИ
Логічні закони і відношення логічного слідкування
Логічні закони і відношення логічного слідкування

Слайд #31
Употребляйте с пользой время,
Учиться надо по системе:
Сперва хочу вам в долг вменить
На курсы логики ходить.
Ваш ум, нетронутый доныне,
На них приучат к дисциплине,
Чтоб взял он направленья ось,
Не разбредаясь вкривь и вкось.
Гёте “Фауст”
Учиться надо по системе:
Сперва хочу вам в долг вменить
На курсы логики ходить.
Ваш ум, нетронутый доныне,
На них приучат к дисциплине,
Чтоб взял он направленья ось,
Не разбредаясь вкривь и вкось.
Гёте “Фауст”

Слайд #32
У математичній логіці за допомогою операцій
з одних висловлень утворюють нові, складніші висловлення.
Наприклад:
.
Такі висловлення прийнято називати формулами або логічними виразами (причому кожна буква, яка позначає висловлення, також є формулою).
з одних висловлень утворюють нові, складніші висловлення.
Наприклад:
.
Такі висловлення прийнято називати формулами або логічними виразами (причому кожна буква, яка позначає висловлення, також є формулою).

Слайд #33
Порядок виконання операцій над висловленнями регулюють дужками так, як це роблять, виконуючи операції над алгебраїчними виразами.
Якщо у виразі немає дужок, то порядок виконання операцій такий:
заперечення,
кон'юнкція,
диз'юнкція,
Імплікація,
еквіваленція
3
Наприлад:
.
Якщо у виразі немає дужок, то порядок виконання операцій такий:
заперечення,
кон'юнкція,
диз'юнкція,
Імплікація,
еквіваленція
3
Наприлад:
.

Слайд #34
А
В
С
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Наприклад: Складіть таблицю істинності для виразу
.
В
С
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
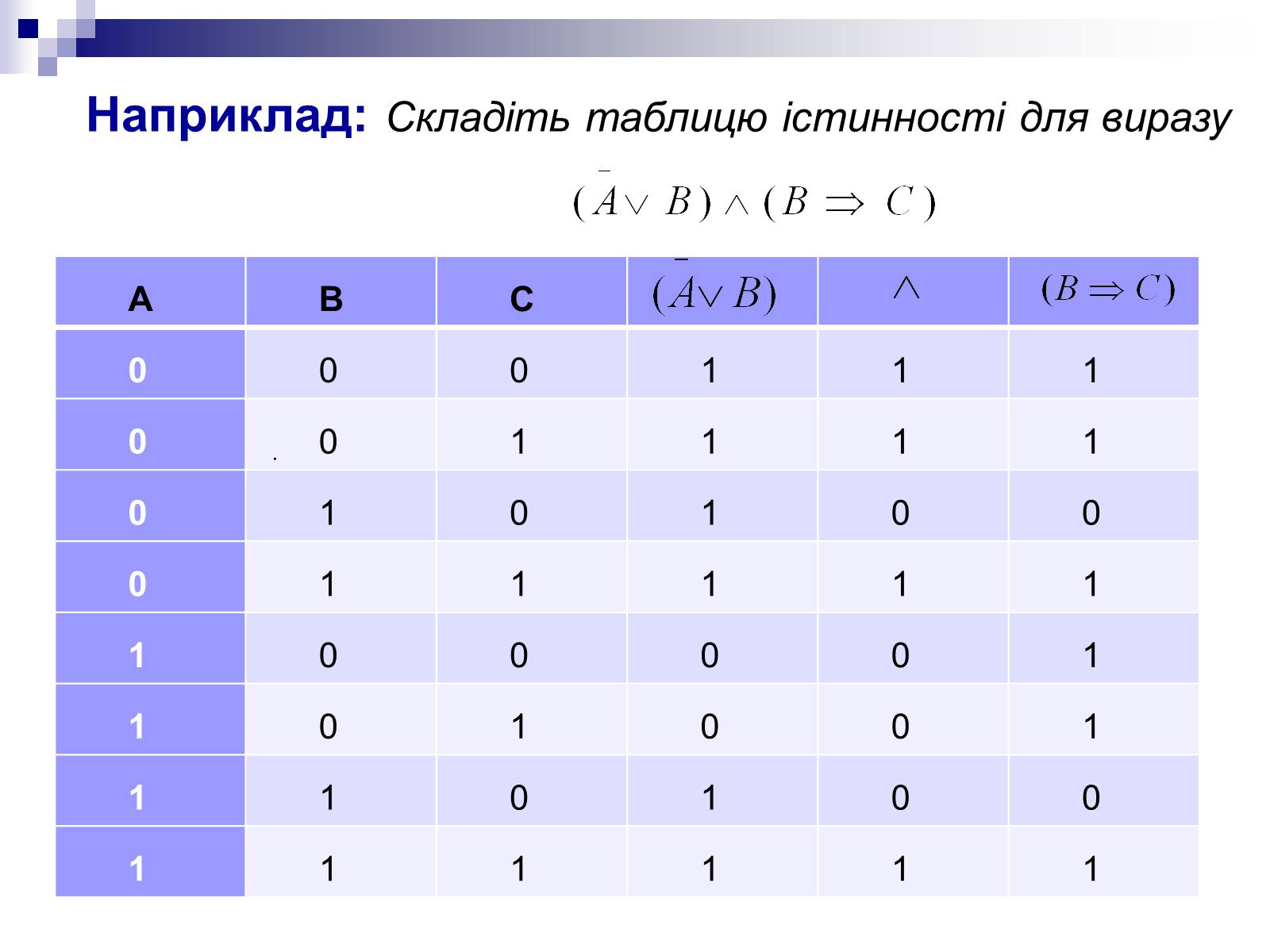
Наприклад: Складіть таблицю істинності для виразу
.
Слайд #35
Висловлювання А і В називають логічно еквівалентними, якщо вони обидва істинні, або обидва хибні ( А=В ).
Два вирази (формули) називаються рівносильними, якщо вини при однакових значеннях букв набувають однакових логічних значень ( А В).
Два вирази (формули) називаються рівносильними, якщо вини при однакових значеннях букв набувають однакових логічних значень ( А В).

Слайд #36
Важливі рівносильності:
1.
1. - закон подвійного заперечення;
переставна властивість для ;
2.
3.
4.
5.
6.
7.
сполучна властивість для
;
перша розподільна
властивість для ;
;
друга розподільна
властивість для ;
1.
1. - закон подвійного заперечення;
переставна властивість для ;
2.
3.
4.
5.
6.
7.
сполучна властивість для
;
перша розподільна
властивість для ;
;
друга розподільна
властивість для ;

Слайд #37
Важливі рівносильності:
8.
9.
10.
11.
12.
13.
14.
закон де Моргана;
- закон виключення третього;
8.
9.
10.
11.
12.
13.
14.
закон де Моргана;
- закон виключення третього;

Слайд #38
Сукупність усіх висловлень разом з визначеними на ній операціями і основними властивостями цих операцій становить алгебру висловлень.
Вирази алгебри висловлень називаються тотожно істинними ( тавтологіями ) або логічними законами, якщо для будь-яких наборів значень букв, які входять до них, ці вирази набувають тільки істинних значень.
Вирази алгебри висловлень називаються тотожно істинними ( тавтологіями ) або логічними законами, якщо для будь-яких наборів значень букв, які входять до них, ці вирази набувають тільки істинних значень.

Слайд #39
Поширені логічні закони:
- закон включення третього: кожне
висловлення або істинне або хибне, і
третього бути не може;
- закон тотожності: кожне висловлення
є логічним висновком із самого себе;
3. - закон суперечності: неправильно,
що висловлення одночасно може бути
істинним і хибним;
- правило висновку: висновок В з
імплікації є висновком з неї і
її умови А;
- закон включення третього: кожне
висловлення або істинне або хибне, і
третього бути не може;
- закон тотожності: кожне висловлення
є логічним висновком із самого себе;
3. - закон суперечності: неправильно,
що висловлення одночасно може бути
істинним і хибним;
- правило висновку: висновок В з
імплікації є висновком з неї і
її умови А;

Слайд #40
5. - правило заперечення умови
6. - правило силогізму
7. - правило контропозиції:
6. - правило силогізму
7. - правило контропозиції:

Слайд #41
Наприклад:
Визначити істинність твердження: «Якщо трикутник рівнобедрений, то дві його сторони рівні; якщо дві сторони трикутника рівні, то два кути його рівні: отже, якщо трикутник рівнобедрений, то два кути його рівні.»
Визначити істинність твердження: «Якщо трикутник рівнобедрений, то дві його сторони рівні; якщо дві сторони трикутника рівні, то два кути його рівні: отже, якщо трикутник рівнобедрений, то два кути його рівні.»

Слайд #42
Розв'язання:
У цьому твердженні можна виділити три змінні висловлення:
А= {трикутник рівнобедрений};
В = {дві сторони трикутника рівні};
С = {два кути трикутника рівні}.
Першу умову міркування запишемо:
, другу -
і висновок –
.
Дане твердження можна записати формулою:
. Ця формула є логічним законом (6), тобто твердження логічно правильне.
У цьому твердженні можна виділити три змінні висловлення:
А= {трикутник рівнобедрений};
В = {дві сторони трикутника рівні};
С = {два кути трикутника рівні}.
Першу умову міркування запишемо:
, другу -
і висновок –
.
Дане твердження можна записати формулою:
. Ця формула є логічним законом (6), тобто твердження логічно правильне.

Слайд #43
1. З висловлень А і В побудувати висловлення:
і знайти значення їх істинності, якщо:
а) А = {число 14612 ділиться на 9}, В = {сума цифр числа 14612 ділиться на 9};
б) А = {діагоналі прямокутника не рівні між собою}, В = {вертикальні кули рівні};
в) А = {існують такі значення m, для яких рівняння 5х=m, не має розв'язку в Z}, В = {рівняння mх=5 має розв'язок в Q для будь-яких значень m};
Розв'язування вправ:
і знайти значення їх істинності, якщо:
а) А = {число 14612 ділиться на 9}, В = {сума цифр числа 14612 ділиться на 9};
б) А = {діагоналі прямокутника не рівні між собою}, В = {вертикальні кули рівні};
в) А = {існують такі значення m, для яких рівняння 5х=m, не має розв'язку в Z}, В = {рівняння mх=5 має розв'язок в Q для будь-яких значень m};
Розв'язування вправ:

Слайд #44
2. Нехай А = {зараз ранок}, В = {зараз тиха погода}, С = {зараз накрапає дощ}. Записані за допомогою формул висловлення сформулювати словами:
а)
б)
в)
г)
д)
а)
б)
в)
г)
д)

Слайд #45
1. Опрацювати записи конспекту.
2. Вивчити основні означення.
3. Виконати завдання:
№ 1: Нехай А = {Микола вміє малювати}, В = {Петро пише вірші}. Записати у вигляді формул такі висловлення:
а) Микола вміє малювати і Петро пише вірші.
б) Микола не вміє малювати або Петро пише вірші.
в) Петро не пише вірші або Микола не вміє малювати.
г) Неправильно, що Микола вміє малювати або Петро не пише вірші.
д) Якщо Петро не пише вірші, то Микола вміє малювати.
Домашнє завдання:
2. Вивчити основні означення.
3. Виконати завдання:
№ 1: Нехай А = {Микола вміє малювати}, В = {Петро пише вірші}. Записати у вигляді формул такі висловлення:
а) Микола вміє малювати і Петро пише вірші.
б) Микола не вміє малювати або Петро пише вірші.
в) Петро не пише вірші або Микола не вміє малювати.
г) Неправильно, що Микола вміє малювати або Петро не пише вірші.
д) Якщо Петро не пише вірші, то Микола вміє малювати.
Домашнє завдання:

Слайд #46
№2: Записати твердження логіко-математичною символікою і визначити істинність чи хибність їх:
1) Якщо 3219 кратне 111, то 3219 кратне 37, а якщо 3219 не кратне 37, то 3219 не кратне 111.
Якщо 3221 кратне 111, то 3221 кратне 37.
3) Якщо 3256 кратне 111, то 3256 кратне 37.
4) х2> 4 тоді і тільки тоді, коли х> 2 або х< -2.
5) х2> 4 тоді і тільки тоді, коли х> 2 і х< -2.
6) х2< 4 тоді і тільки тоді, коли х< 2 іх> -2.
7) х2< 4 тоді і тільки тоді, коли х< 2 або х>-2.
1) Якщо 3219 кратне 111, то 3219 кратне 37, а якщо 3219 не кратне 37, то 3219 не кратне 111.
Якщо 3221 кратне 111, то 3221 кратне 37.
3) Якщо 3256 кратне 111, то 3256 кратне 37.
4) х2> 4 тоді і тільки тоді, коли х> 2 або х< -2.
5) х2> 4 тоді і тільки тоді, коли х> 2 і х< -2.
6) х2< 4 тоді і тільки тоді, коли х< 2 іх> -2.
7) х2< 4 тоді і тільки тоді, коли х< 2 або х>-2.

Слайд #47
ДЖОРДЖ БУЛЬ(1815-1864 гг.)
Дж.Буль автор известный произведений «Математический анализ логики»(1847г.)
Основной труд Дж. Буля «Исследование законов мысли», в ней представлен раздел логики- алгебра высказываний.
В 1844 г. Буль получает золотую медаль за работ по математическому анализу.
БиографияДж. Буль.doc
Дж.Буль автор известный произведений «Математический анализ логики»(1847г.)
Основной труд Дж. Буля «Исследование законов мысли», в ней представлен раздел логики- алгебра высказываний.
В 1844 г. Буль получает золотую медаль за работ по математическому анализу.
БиографияДж. Буль.doc

Слайд #48
БУЛЕВА АЛГЕБРА
Правила сложения (дизъюнкция) в булевой алгебре выглядят так:
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 1
Сложение обозначается «или», «+», «v».
1. Умножение классов, обозначился «·» и в настоящее время эта операция называется «конъюнкцией» или «пересечением» и обозначается символами «?» «&» «И»
Правила умножения (конъюнкция) булевой алгебре:
0 · 0 = 0
1 · 0 = 0
0 · 1= 0
1 · 1 = 1
Дополнение класса (инверсия), для обозначения класса используется «Â» «не» и называется операцией отрицанием.
Не 0 = 1
Не 1 = 0
Правила сложения (дизъюнкция) в булевой алгебре выглядят так:
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 1
Сложение обозначается «или», «+», «v».
1. Умножение классов, обозначился «·» и в настоящее время эта операция называется «конъюнкцией» или «пересечением» и обозначается символами «?» «&» «И»
Правила умножения (конъюнкция) булевой алгебре:
0 · 0 = 0
1 · 0 = 0
0 · 1= 0
1 · 1 = 1
Дополнение класса (инверсия), для обозначения класса используется «Â» «не» и называется операцией отрицанием.
Не 0 = 1
Не 1 = 0

Слайд #49
ОСНОВНОЙ ЗАКОН БУЛЯ
Основным законом алгебры Буля является закон идемпотентности, в соответствии с которым исключаются все коэффициенты и показатели степеней.
А+А+А+А=А
А·А·А=А
если заменить символ А на 2, то в булевой алгебре будет:2 + 2 = 2
Точно также и умножение :
А·А·А·А = А 2·2=2
Основным законом алгебры Буля является закон идемпотентности, в соответствии с которым исключаются все коэффициенты и показатели степеней.
А+А+А+А=А
А·А·А=А
если заменить символ А на 2, то в булевой алгебре будет:2 + 2 = 2
Точно также и умножение :
А·А·А·А = А 2·2=2

Слайд #50
ВОПРОСЫ
1.В академии какого философа учился и работал Аристотель?
2.Кто был воспитанником у Аристотеля?
3.Как называлось школа, которую создал Аристотель?
4.В каком городе находился университет, который он закончил tЛейбниц?
5.Кто из ученых ввел символы для обозначения высказываний?
6.Кому принадлежит идея логического исчисления?
7.В каких годах жил и работал Джордж Буль?
8.В каком году вышла в свет книга «Исследование законов мысли»?
. 9.Как записывается закон идемпотентности?
10.Какие основные булевы операции вы знаете? Запишите в тетрадь правила логического сложения, умножения, отрицания.
1.В академии какого философа учился и работал Аристотель?
2.Кто был воспитанником у Аристотеля?
3.Как называлось школа, которую создал Аристотель?
4.В каком городе находился университет, который он закончил tЛейбниц?
5.Кто из ученых ввел символы для обозначения высказываний?
6.Кому принадлежит идея логического исчисления?
7.В каких годах жил и работал Джордж Буль?
8.В каком году вышла в свет книга «Исследование законов мысли»?
. 9.Как записывается закон идемпотентности?
10.Какие основные булевы операции вы знаете? Запишите в тетрадь правила логического сложения, умножения, отрицания.

Слайд #51
ФОРМЫ МЫШЛЕНИЯ

Слайд #52
ЛОГИКА– это наука о формах и способах мышления
Аристотель отделил формы мышления от его содержания
Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны.
Мышления всегда существует в каких – то формах – это понятие, высказывание, умозаключение.
Аристотель отделил формы мышления от его содержания
Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны.
Мышления всегда существует в каких – то формах – это понятие, высказывание, умозаключение.

Слайд #53
ПОНЯТИЕ – это форма мышление, которая фиксирующая основные, существенные признаки объекта.
Понятие имеет две стороны: содержание и объем.
Содержание это совокупность признаков объекта.
Объем – это совокупность (количество объектов ) на которые эти признаки распространяются.
Понятие имеет две стороны: содержание и объем.
Содержание это совокупность признаков объекта.
Объем – это совокупность (количество объектов ) на которые эти признаки распространяются.

Слайд #54
ВЫСКАЗЫВАНИЕ – это форма мышления. В которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть истинно или ложно.
Свое понимание окружающего мира человек формулирует в форме высказываний.(суждений, утверждений). Высказывание строиться на основе понятий и по форме является повествовательным предложением. Высказывание об объекте может быть истинным или ложным.
Высказывание не может быть вопросительным или повелительным т.к. оценка истинности или ложности невозможна. Истинность является величиной относительной, и завесит от многих причин и обстоятельств.
Ссылка:формы_мышлен.doc
Свое понимание окружающего мира человек формулирует в форме высказываний.(суждений, утверждений). Высказывание строиться на основе понятий и по форме является повествовательным предложением. Высказывание об объекте может быть истинным или ложным.
Высказывание не может быть вопросительным или повелительным т.к. оценка истинности или ложности невозможна. Истинность является величиной относительной, и завесит от многих причин и обстоятельств.
Ссылка:формы_мышлен.doc

Слайд #55
УМОЗАКЛЮЧЕНИЕ – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение (заключение).
Умозаключение позволяет на основе известных фактов, выраженных в форме высказываний, получить заключение, т.е. новое знание.(геометр. док-ва)
Посылками умозаключения могут быть только истинные суждения, тогда заключение будет истинным, в противном случае можно прийти к ложному умозаключению.(по подробнее можно прочесть по гиперссылке формы_мышлен.doc
Умозаключение позволяет на основе известных фактов, выраженных в форме высказываний, получить заключение, т.е. новое знание.(геометр. док-ва)
Посылками умозаключения могут быть только истинные суждения, тогда заключение будет истинным, в противном случае можно прийти к ложному умозаключению.(по подробнее можно прочесть по гиперссылке формы_мышлен.doc

Слайд #56
ВОПРОСЫ
1 Определение формы понятие.
2 Чем характеризуется понятие?
3 Придумайте примеры понятий об объектах: квадрат, стол, вода.
4 Определение высказывания.
5 Какие значения принимает высказывание ?
6 Может ли суждение высказанное в повелительной форме являться высказыванием? Привести пример.
7 Придумайте и запишите в тетрадь простые высказывания.
8 Придумайте и запишите в тетрадь сложные высказывания.
1 Определение формы понятие.
2 Чем характеризуется понятие?
3 Придумайте примеры понятий об объектах: квадрат, стол, вода.
4 Определение высказывания.
5 Какие значения принимает высказывание ?
6 Может ли суждение высказанное в повелительной форме являться высказыванием? Привести пример.
7 Придумайте и запишите в тетрадь простые высказывания.
8 Придумайте и запишите в тетрадь сложные высказывания.

Слайд #57
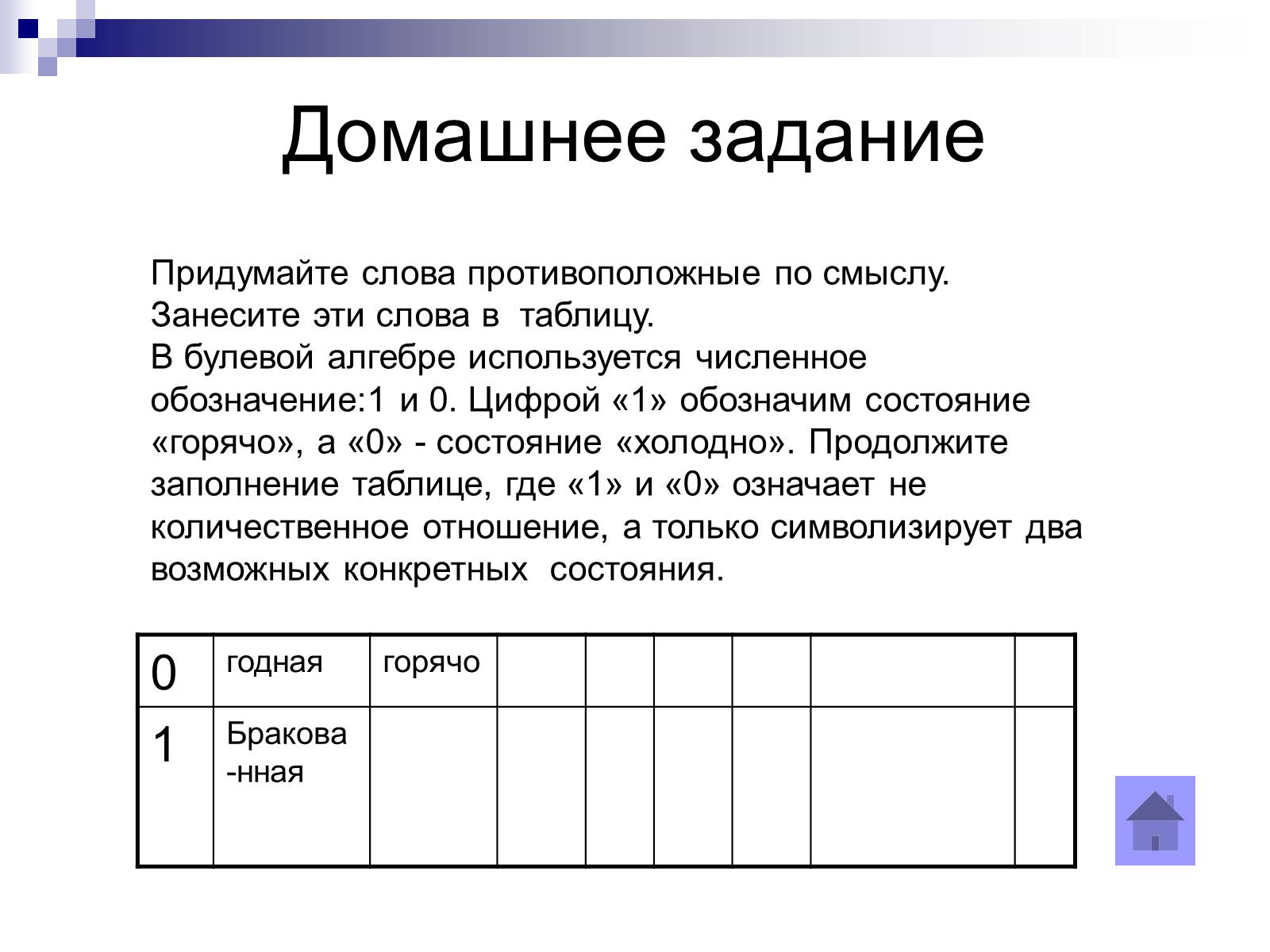
Домашнее задание
годная
горячо
1
Бракова-нная
Придумайте слова противоположные по смыслу. Занесите эти слова в таблицу.
В булевой алгебре используется численное обозначение:1 и 0. Цифрой «1» обозначим состояние «горячо», а «0» - состояние «холодно». Продолжите заполнение таблице, где «1» и «0» означает не количественное отношение, а только символизирует два возможных конкретных состояния.
годная
горячо
1
Бракова-нная
Придумайте слова противоположные по смыслу. Занесите эти слова в таблицу.
В булевой алгебре используется численное обозначение:1 и 0. Цифрой «1» обозначим состояние «горячо», а «0» - состояние «холодно». Продолжите заполнение таблице, где «1» и «0» означает не количественное отношение, а только символизирует два возможных конкретных состояния.