- Головна
- Готові шкільні презентації
- Презентація на тему «Об’єм циліндра»
Презентація на тему «Об’єм циліндра»
665
Слайд #1
Об'єм циліндра
Слайд #2
Тема уроку:
поняття про циліндр як тіло обертання, його основні елементи, формули для обчислення об'єму, площі
поняття про циліндр як тіло обертання, його основні елементи, формули для обчислення об'єму, площі

Слайд #3
Мета уроку:
формування поняття про циліндр, основи і твірні циліндра;
радіус, висоту та вісь циліндра;
перерізи циліндра
площу і об'єм циліндра;
вивчення властивостей основ і твірних циліндра;
формули для обчислення площ бічної і повної поверхні циліндра; розгляд кількох задач з теми
формування поняття про циліндр, основи і твірні циліндра;
радіус, висоту та вісь циліндра;
перерізи циліндра
площу і об'єм циліндра;
вивчення властивостей основ і твірних циліндра;
формули для обчислення площ бічної і повної поверхні циліндра; розгляд кількох задач з теми

Слайд #4
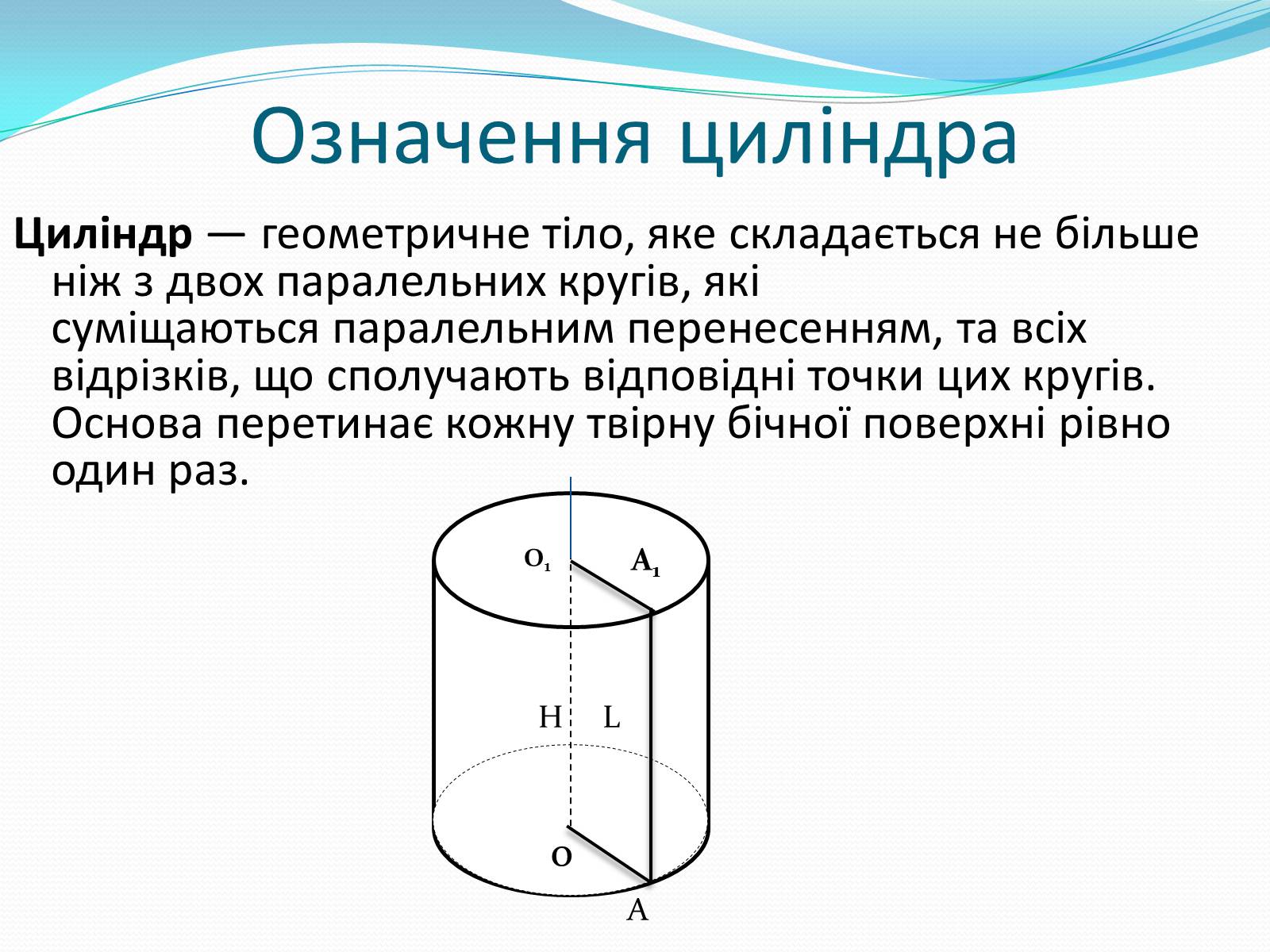
Означення циліндра
Циліндр — геометричне тіло, яке складається не більше ніж з двох паралельних кругів, які суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих кругів. Основа перетинає кожну твірну бічної поверхні рівно один раз.
о
О1
А
А1
Н
L
Циліндр — геометричне тіло, яке складається не більше ніж з двох паралельних кругів, які суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих кругів. Основа перетинає кожну твірну бічної поверхні рівно один раз.
о
О1
А
А1
Н
L
Слайд #5
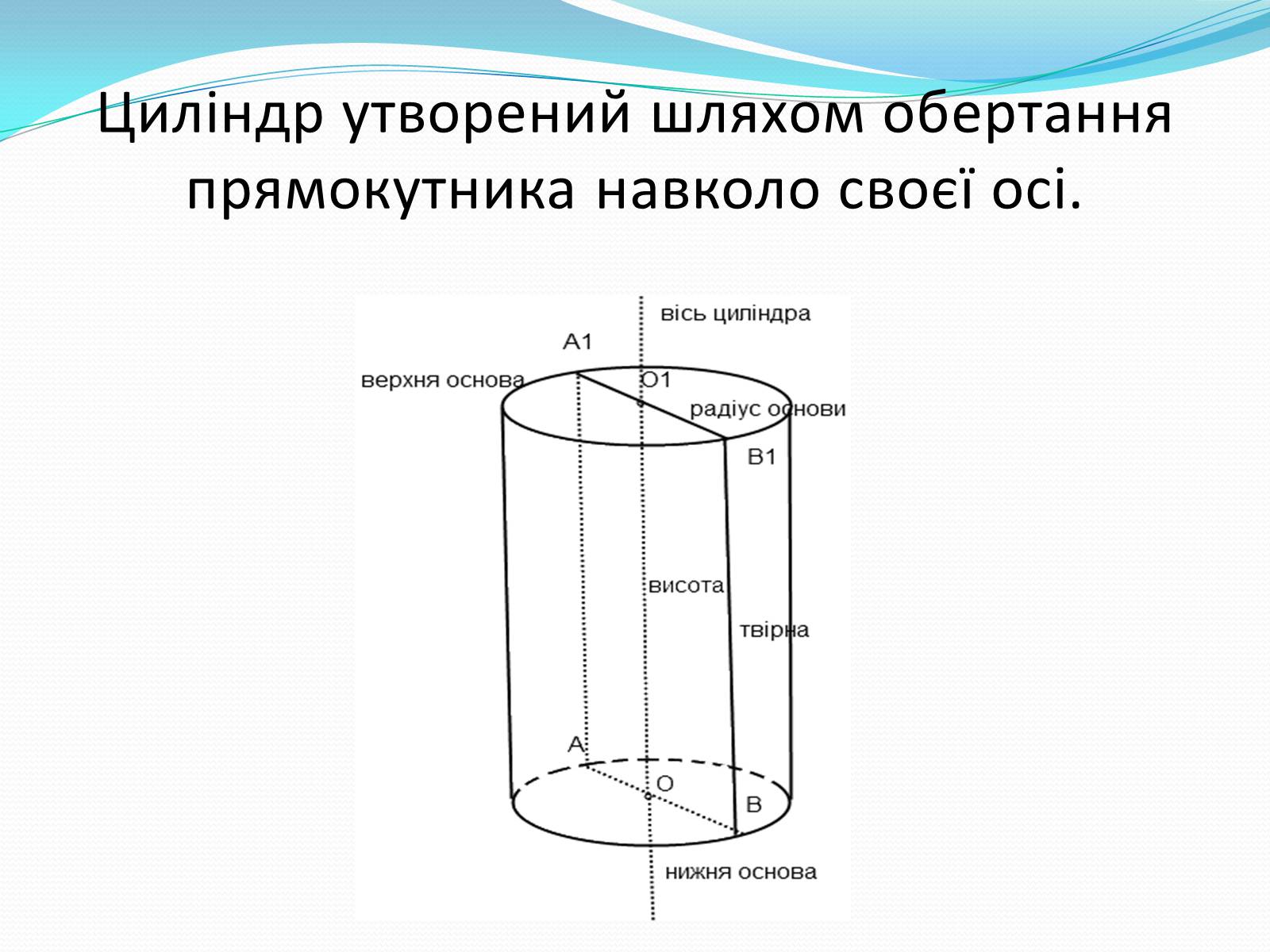
Циліндр утворений шляхом обертання прямокутника навколо своєї осі.
Слайд #6
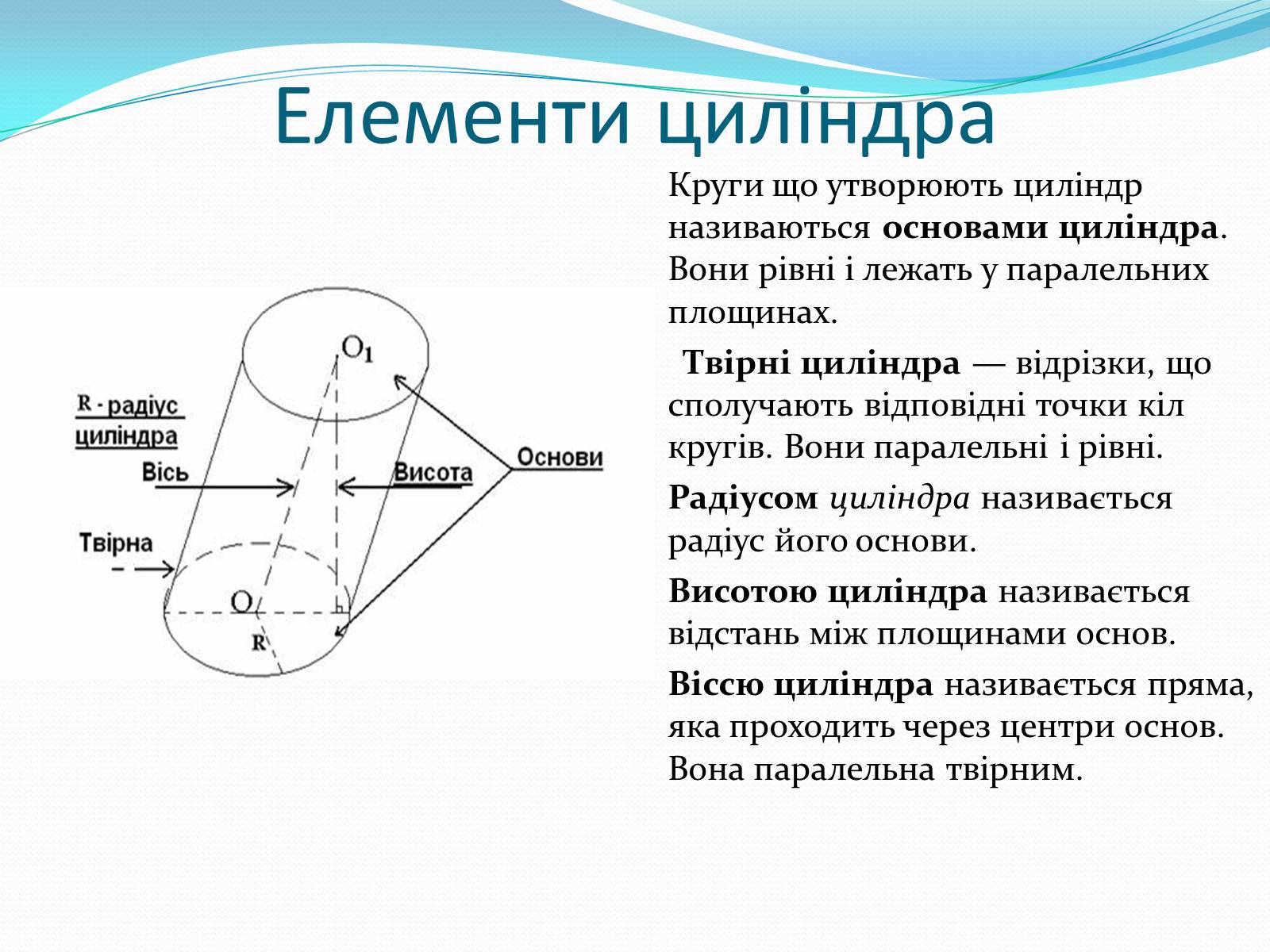
Елементи циліндра
Круги що утворюють циліндр називаються основами циліндра. Вони рівні і лежать у паралельних площинах.
Твірні циліндра — відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні і рівні.
Радіусом циліндра називається радіус його основи.
Висотою циліндра називається відстань між площинами основ.
Віссю циліндра називається пряма, яка проходить через центри основ. Вона паралельна твірним.
Круги що утворюють циліндр називаються основами циліндра. Вони рівні і лежать у паралельних площинах.
Твірні циліндра — відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні і рівні.
Радіусом циліндра називається радіус його основи.
Висотою циліндра називається відстань між площинами основ.
Віссю циліндра називається пряма, яка проходить через центри основ. Вона паралельна твірним.
Слайд #7
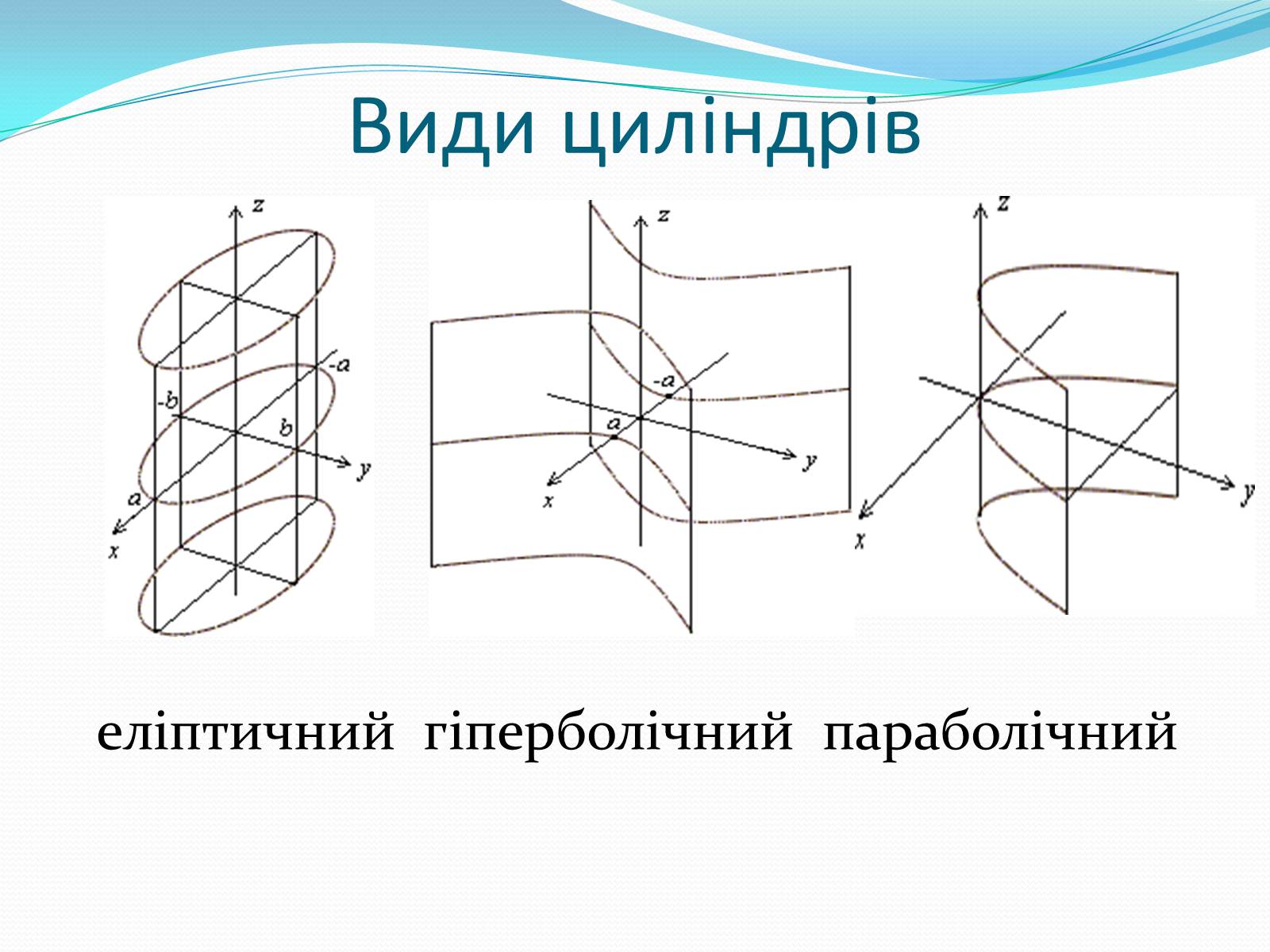
Види циліндрів
еліптичний гіперболічний параболічний
еліптичний гіперболічний параболічний
Слайд #8
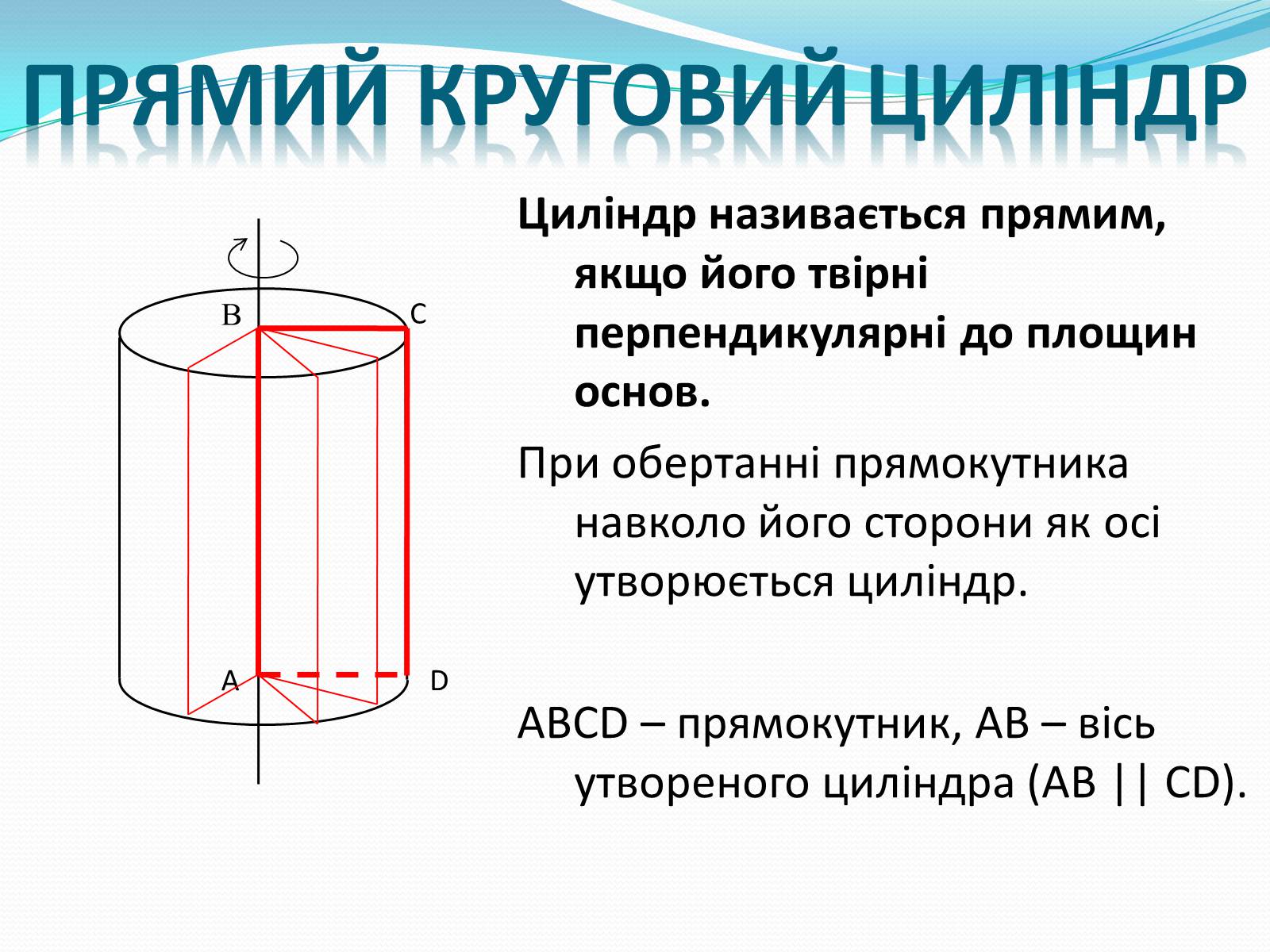
Прямий Круговий циліндр
Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ.
При обертанні прямокутника навколо його сторони як осі утворюється циліндр.
ABCD – прямокутник, АВ – вісь утвореного циліндра (AB || CD).
D
C
А
В
Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ.
При обертанні прямокутника навколо його сторони як осі утворюється циліндр.
ABCD – прямокутник, АВ – вісь утвореного циліндра (AB || CD).
D
C
А
В
Слайд #9
Площа поверхні циліндра
Площа повної поверхні циліндра дорівнює сумі площ його бічної поверхні та його основ.
Площа бічної поверхні циліндра обчислюється за формулою:
R
Площа повної поверхні циліндра дорівнює сумі площ його бічної поверхні та його основ.
Площа бічної поверхні циліндра обчислюється за формулою:
R

Слайд #10
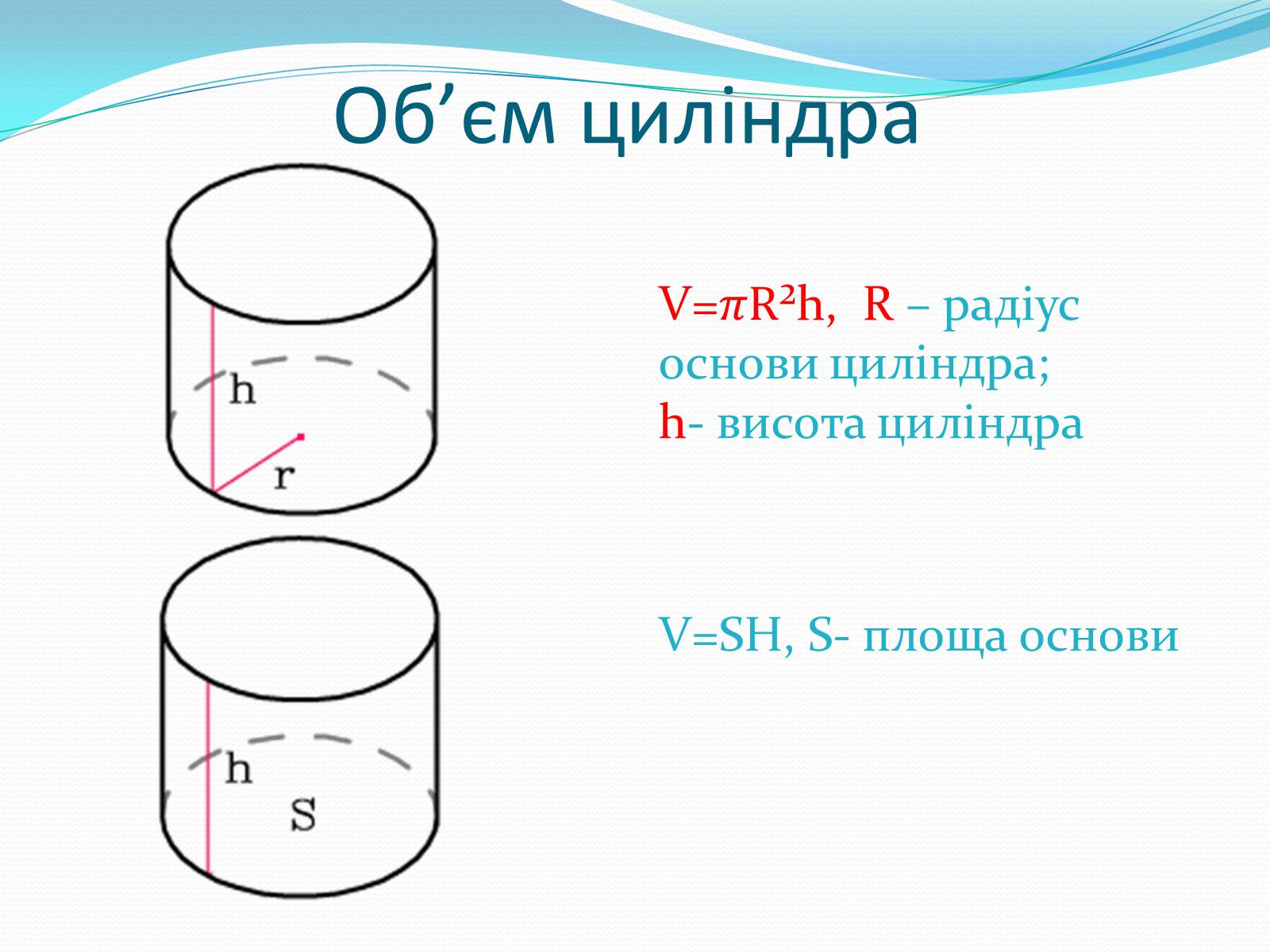
Об'єм циліндра
V=
V=
Слайд #11
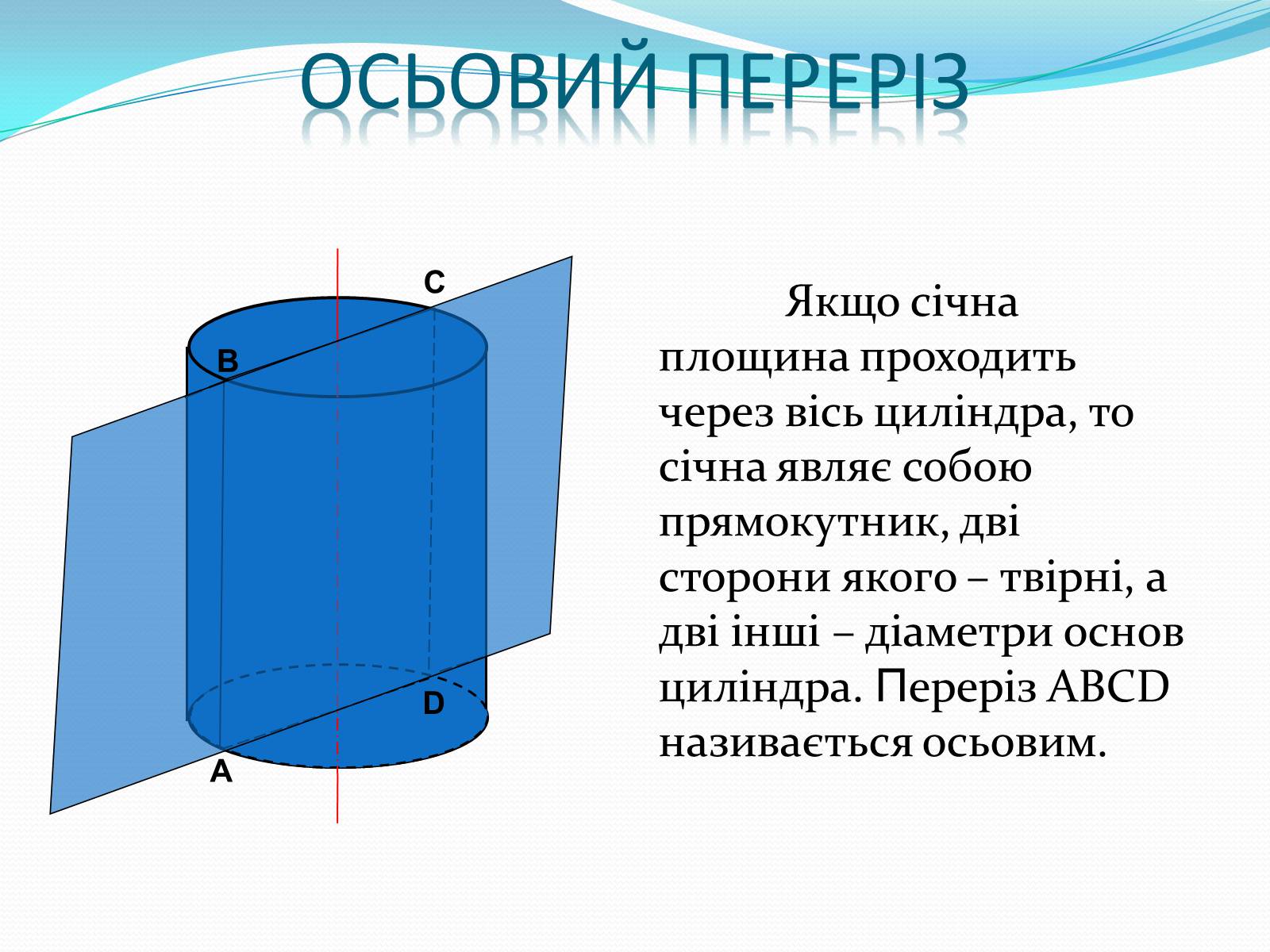
Осьовий переріз
Якщо січна площина проходить через вісь циліндра, то січна являє собою прямокутник, дві сторони якого – твірні, а дві інші – діаметри основ циліндра. Переріз ABCD називається осьовим.
A
D
C
B
Якщо січна площина проходить через вісь циліндра, то січна являє собою прямокутник, дві сторони якого – твірні, а дві інші – діаметри основ циліндра. Переріз ABCD називається осьовим.
A
D
C
B
Слайд #12
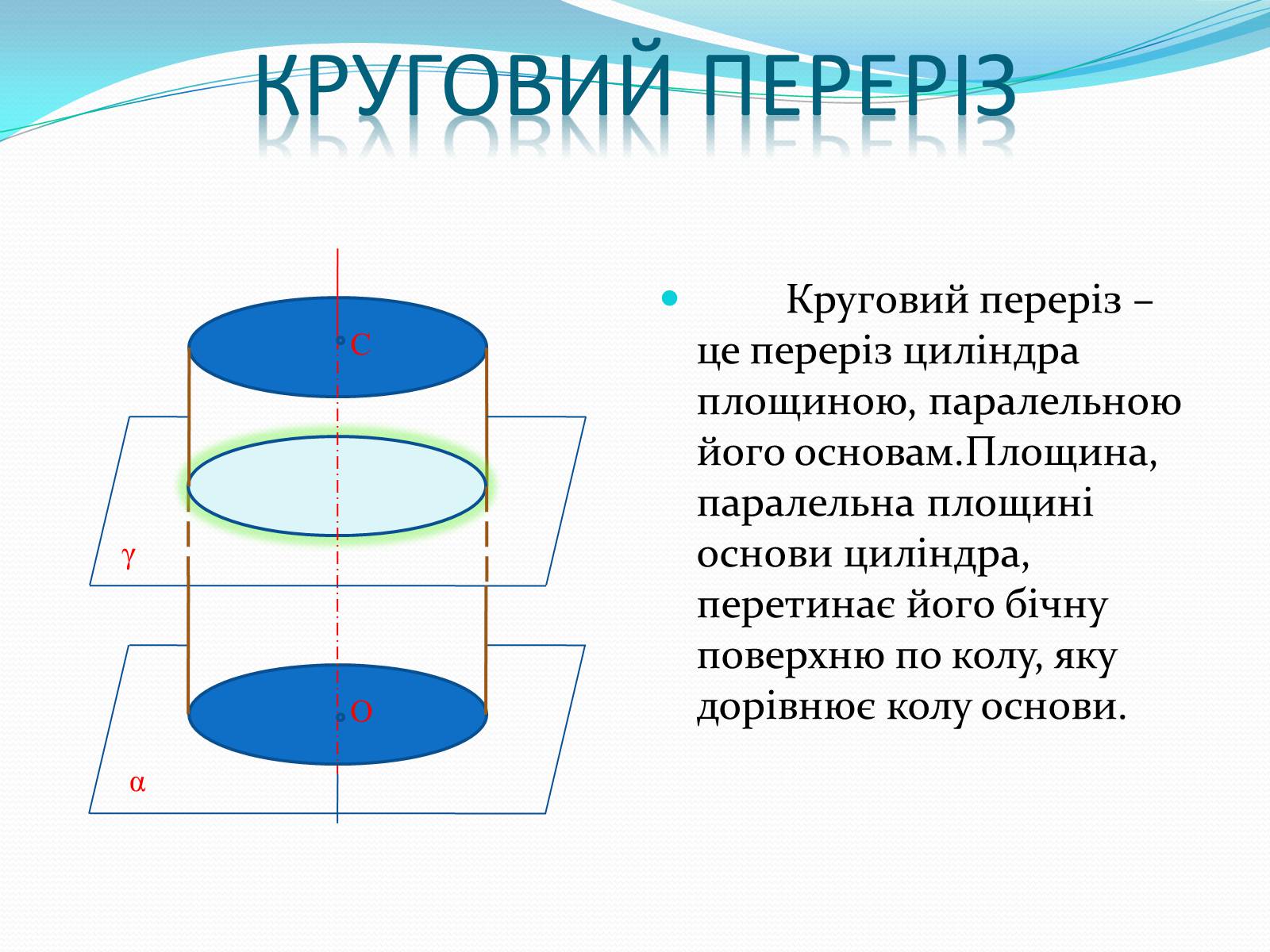
Круговий переріз
Круговий переріз – це переріз циліндра площиною, паралельною його основам.Площина, паралельна площині основи циліндра, перетинає його бічну поверхню по колу, яку дорівнює колу основи.
С
О
γ
α
Круговий переріз – це переріз циліндра площиною, паралельною його основам.Площина, паралельна площині основи циліндра, перетинає його бічну поверхню по колу, яку дорівнює колу основи.
С
О
γ
α
Слайд #13
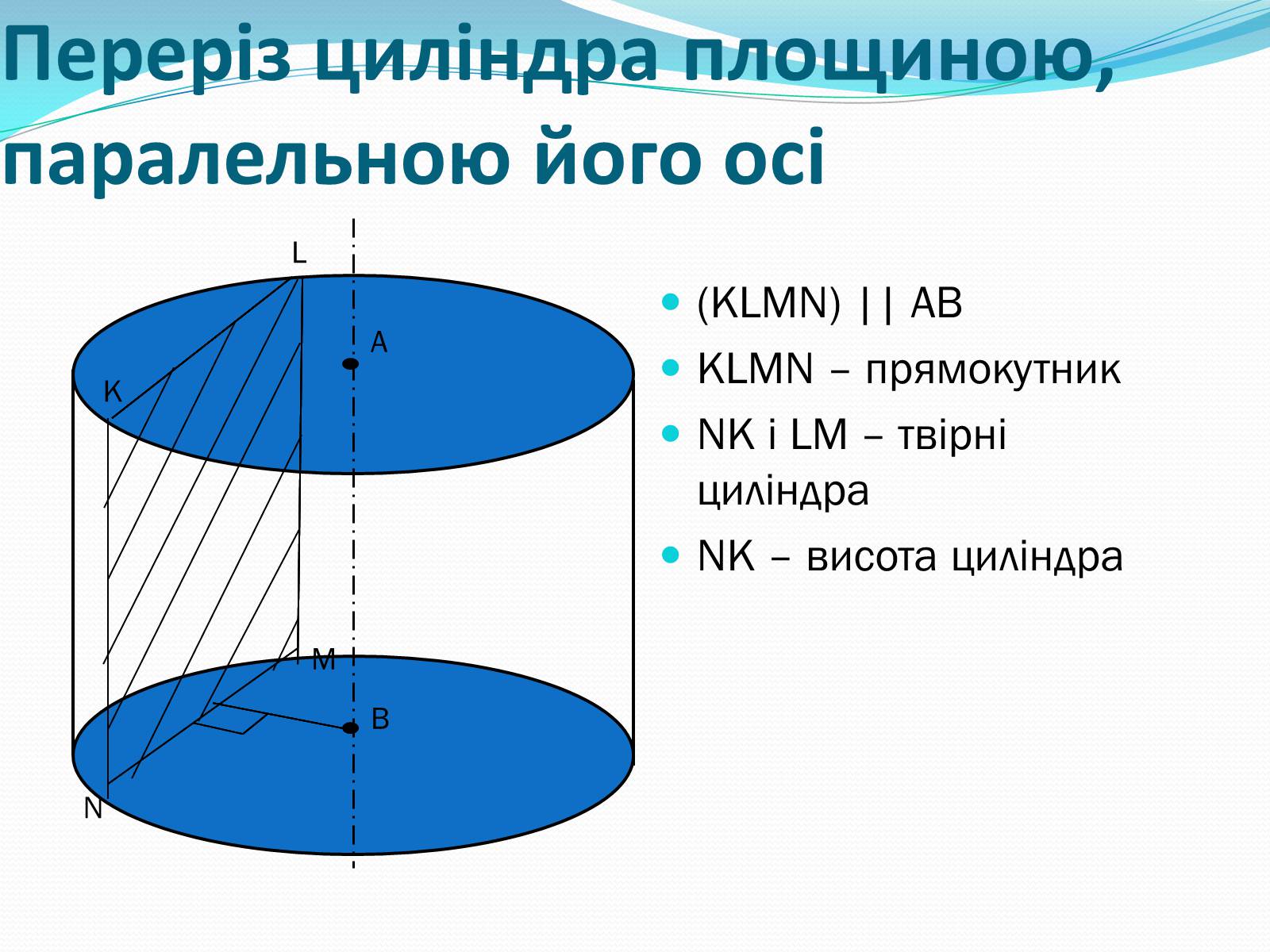
Переріз циліндра площиною, паралельною його осі
(KLMN) || AB
KLMN – прямокутник
NK і LM – твірні циліндра
NK – висота циліндра
A
B
M
K
L
N
(KLMN) || AB
KLMN – прямокутник
NK і LM – твірні циліндра
NK – висота циліндра
A
B
M
K
L
N
Слайд #14
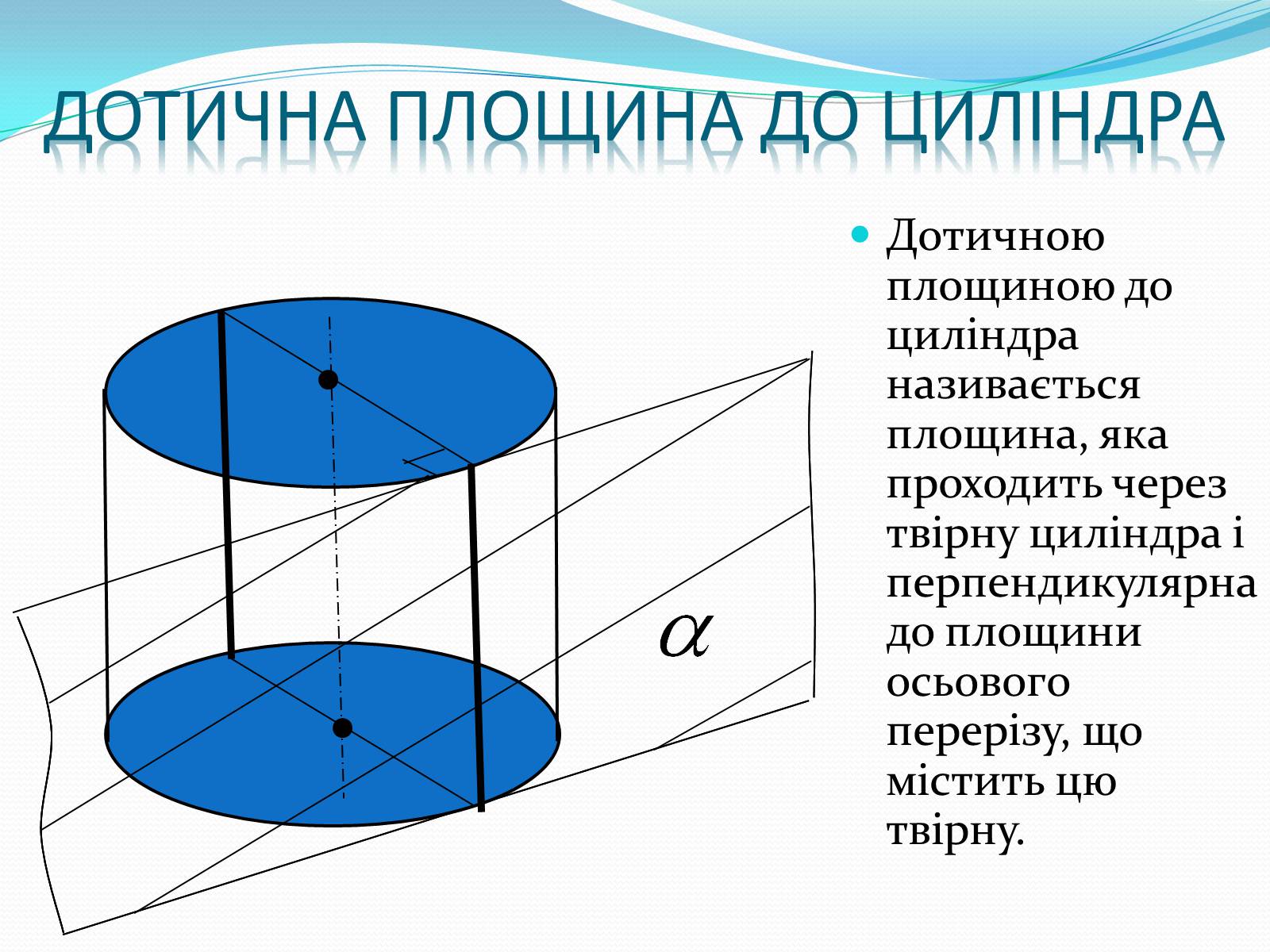
Дотична площина до циліндра
Дотичною площиною до циліндра називається площина, яка проходить через твірну циліндра і перпендикулярна до площини осьового перерізу, що містить цю твірну.
Дотичною площиною до циліндра називається площина, яка проходить через твірну циліндра і перпендикулярна до площини осьового перерізу, що містить цю твірну.
Слайд #15
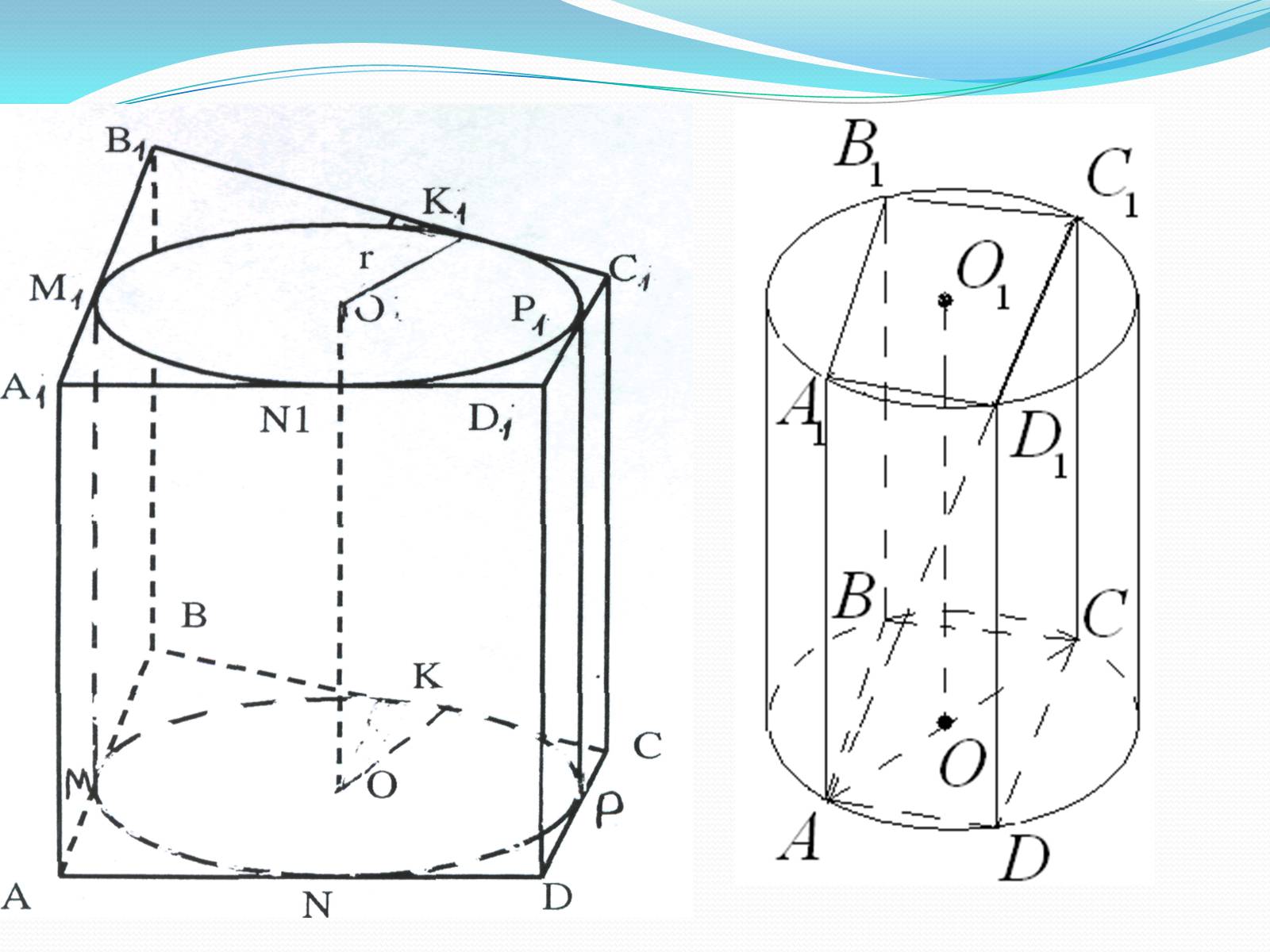
Вписані і описані циліндри
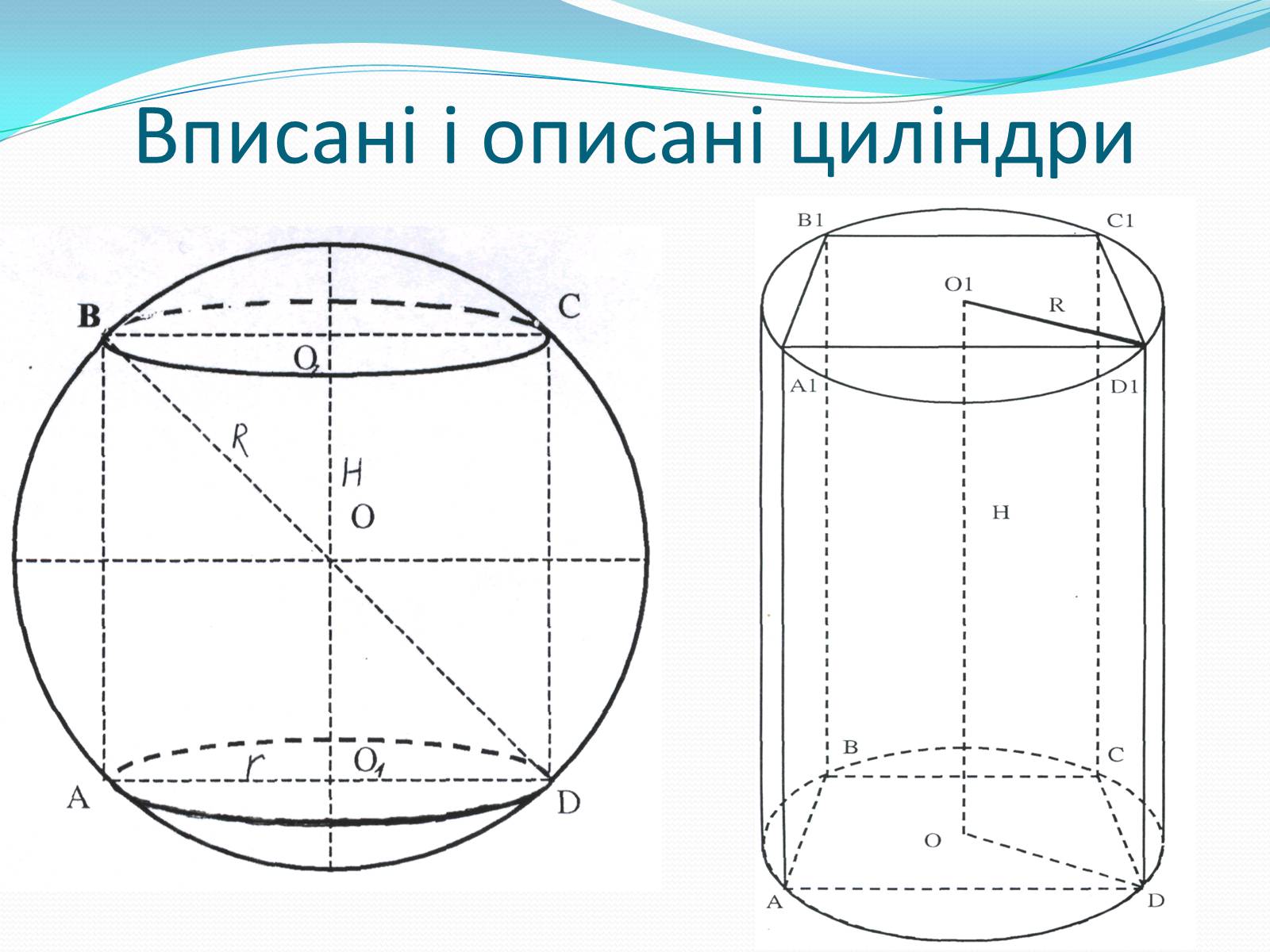
Слайд #16
Вписані і описані циліндри
Слайд #17
Задача №1 В циліндр площа основи дорівнює Q, а площа осьового перерізу S. Визначити повну поверхню циліндра.
Розв'язанння:
Відповідь:
D
A
C
O1
O
Розв'язанння:
Відповідь:
D
A
C
O1
O

Слайд #18
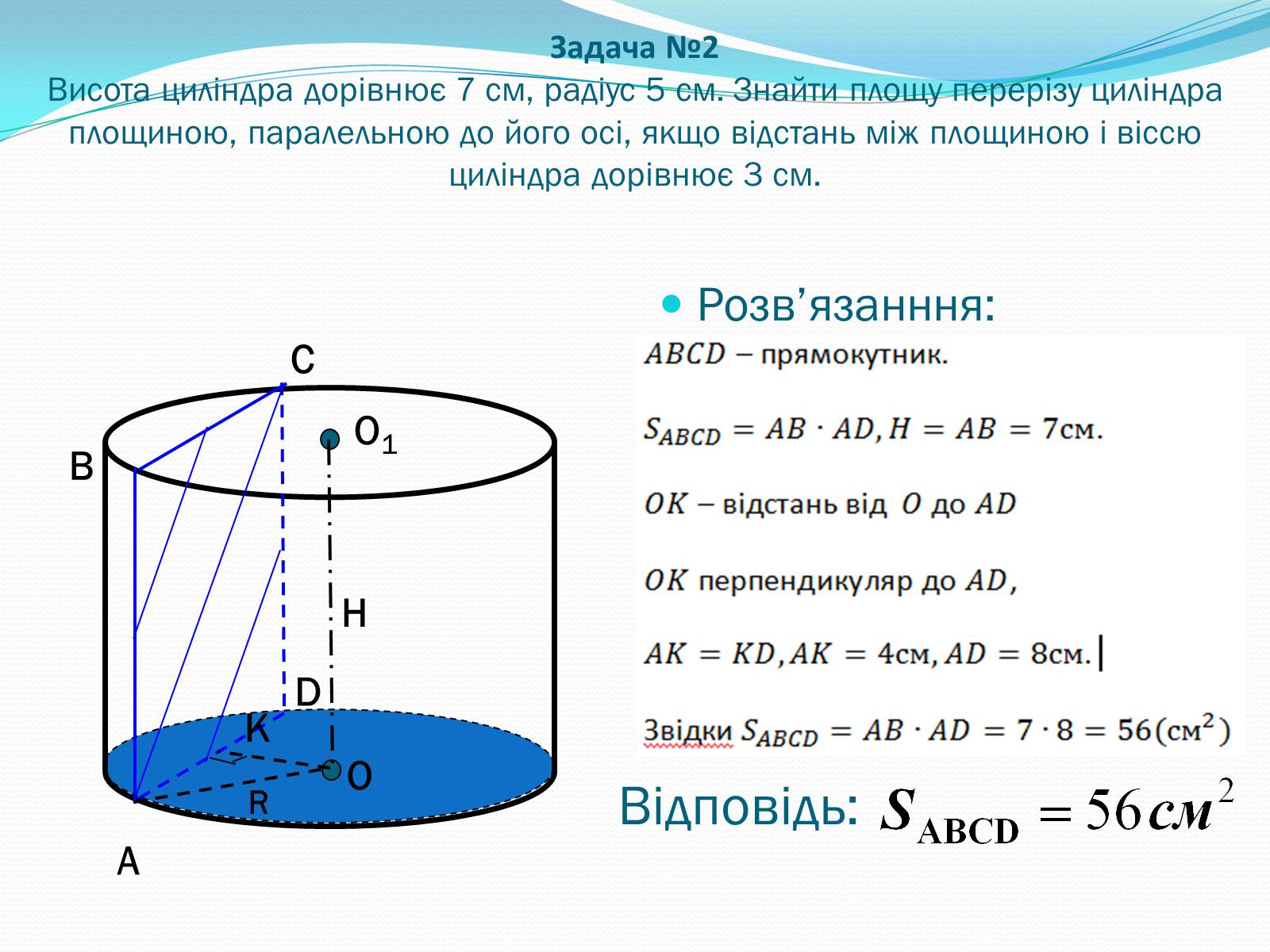
Задача №2Висота циліндра дорівнює 7 см, радіус 5 см. Знайти площу перерізу циліндра площиною, паралельною до його осі, якщо відстань між площиною і віссю циліндра дорівнює 3 см.
Розв'язанння:
Відповідь:
O
O1
A
B
C
D
K
H
R
Розв'язанння:
Відповідь:
O
O1
A
B
C
D
K
H
R
Слайд #19
Використання циліндрів

Слайд #20
Використання циліндрів

Слайд #21
Використання циліндрів

Слайд #22
Використання циліндрів

Слайд #23
Використання циліндрів

Слайд #24
Використання циліндрів

Слайд #25
Висновки
Отже, ми закріпили поняття про циліндр, його основні елементи, види, перерізи,
навчились обчислювати площу поверхні і об'єм циліндра,
побачили приклади його використання в нашому житті
Отже, ми закріпили поняття про циліндр, його основні елементи, види, перерізи,
навчились обчислювати площу поверхні і об'єм циліндра,
побачили приклади його використання в нашому житті
