- Головна
- Готові шкільні презентації
- Презентація на тему «Двугранный и трехгранный угол»
Презентація на тему «Двугранный и трехгранный угол»
309
Слайд #1
Подготовил
Ученик 11-А класса
ЭМЛ
Потоскуев Валерий
Двугранный и трехгранный угол
Ученик 11-А класса
ЭМЛ
Потоскуев Валерий
Двугранный и трехгранный угол

Слайд #2
Двугранный угол

Слайд #3
Определение
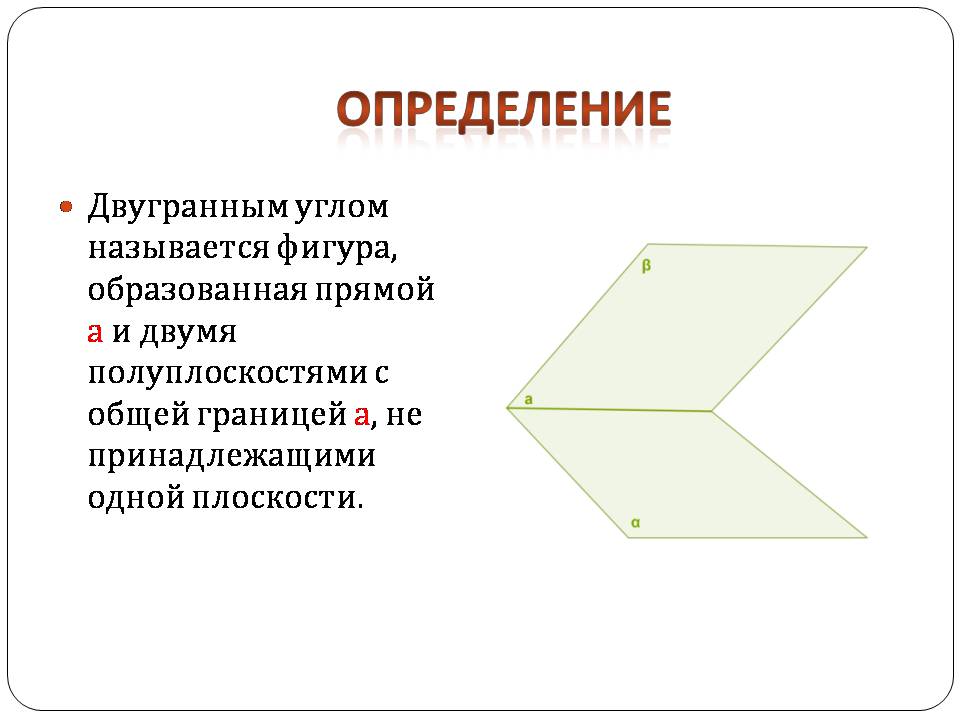
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости.
Слайд #4
Двугранный угол
Градусной мерой двугранного угла называется градусная мера любого из его линейных углов.
Величина двугранного угла находится в пределах от 0° до 180°.
Градусной мерой двугранного угла называется градусная мера любого из его линейных углов.
Величина двугранного угла находится в пределах от 0° до 180°.

Слайд #5
Линейный угол двугранного угла
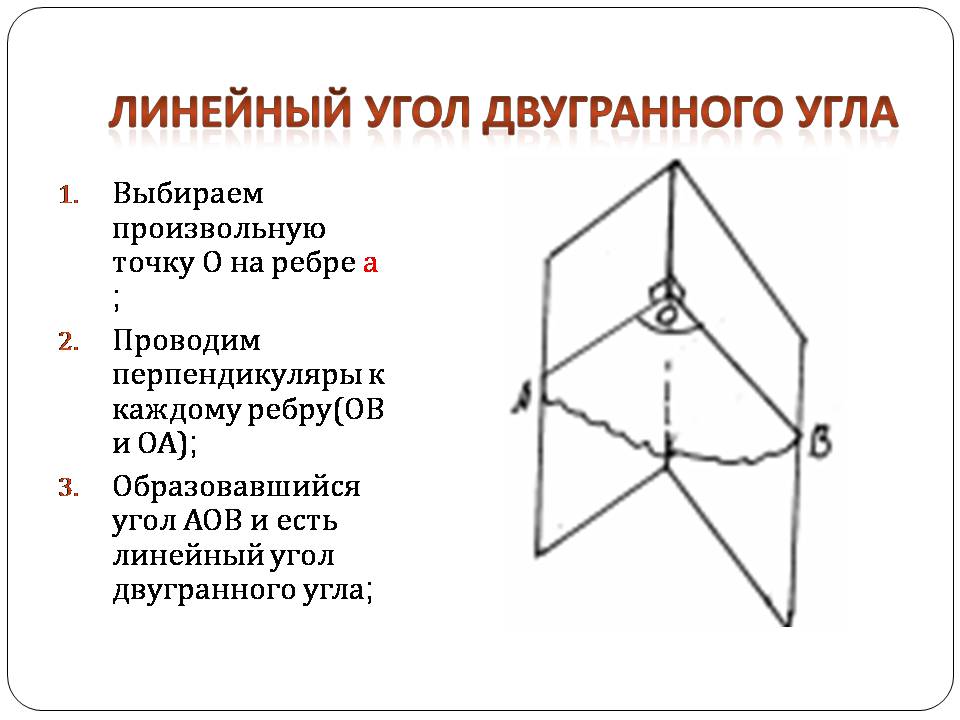
Выбираем произвольную точку О на ребре а ;
Проводим перпендикуляры к каждому ребру(ОВ и ОА);
Образовавшийся угол АОВ и есть линейный угол двугранного угла;
Выбираем произвольную точку О на ребре а ;
Проводим перпендикуляры к каждому ребру(ОВ и ОА);
Образовавшийся угол АОВ и есть линейный угол двугранного угла;
Слайд #6
Все линейные углы двугранного угла равны
Доказательство :
Имеем двугранный угол, т.е. полуплоскости a, b и ребро.
Берем точку О и произвольную точку О1. Строим линейный угол соответствующий точке О, т.е. проводим два перпендикуляра в плоскостях к ребру. Получаем угол АОВ – линейный угол двугранного угла.
Из точки О1 проводим два перпендикуляра к ребру в плоскостях a, b соответственно и получаем второй линейный угол А1О1В1.
Замечаем, что лучи О1А1 и ОА сонаправлены (т.к. Они лежат в одной полуплоскости и параллельны между собой, как два перпендикуляра к одной и той же прямой.)
Вторые лучи О1В1 и ОВ тоже сонаправлены, значит,
ÐАОВ=ÐА1О1В1, как углы с сонаправленными сторонами.
Доказательство :
Имеем двугранный угол, т.е. полуплоскости a, b и ребро.
Берем точку О и произвольную точку О1. Строим линейный угол соответствующий точке О, т.е. проводим два перпендикуляра в плоскостях к ребру. Получаем угол АОВ – линейный угол двугранного угла.
Из точки О1 проводим два перпендикуляра к ребру в плоскостях a, b соответственно и получаем второй линейный угол А1О1В1.
Замечаем, что лучи О1А1 и ОА сонаправлены (т.к. Они лежат в одной полуплоскости и параллельны между собой, как два перпендикуляра к одной и той же прямой.)
Вторые лучи О1В1 и ОВ тоже сонаправлены, значит,
ÐАОВ=ÐА1О1В1, как углы с сонаправленными сторонами.

Слайд #7
Одно из важнейших свойств
Его плоскость перпендикулярна ребру двугранного угла.
Его плоскость перпендикулярна ребру двугранного угла.

Слайд #8
Двугранный угол
Острый (0;90)
Прямой = 90
Тупой (90;180)
Острый (0;90)
Прямой = 90
Тупой (90;180)

Слайд #9
Трехгранный угол

Слайд #10
Определение
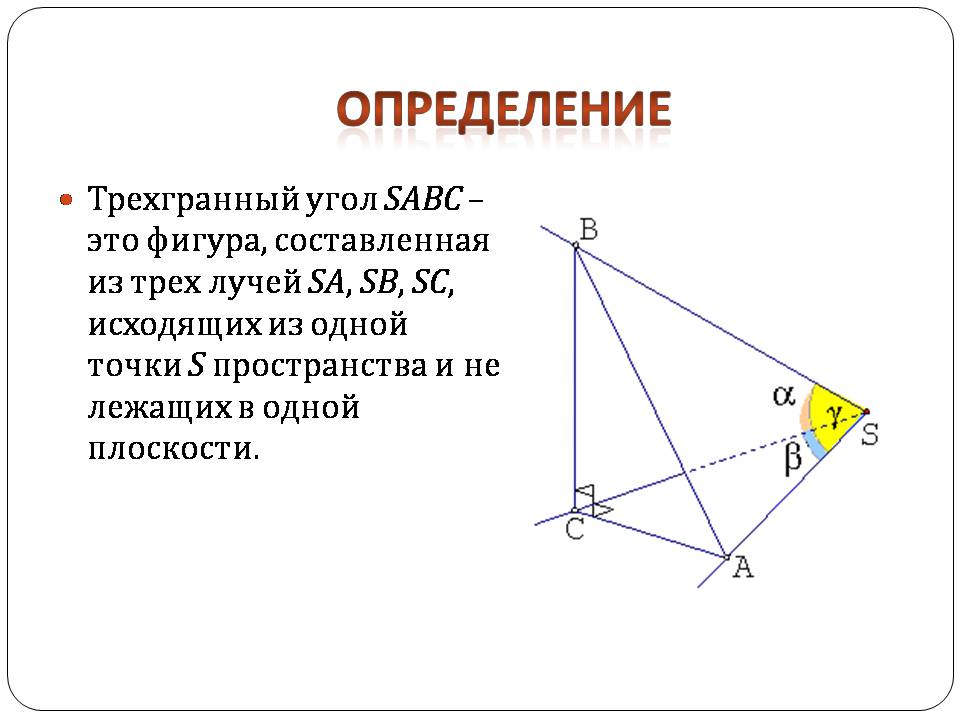
Трехгранный угол SABC – это фигура, составленная из трех лучей SA, SB, SC, исходящих из одной точки S пространства и не лежащих в одной плоскости.
Трехгранный угол SABC – это фигура, составленная из трех лучей SA, SB, SC, исходящих из одной точки S пространства и не лежащих в одной плоскости.
Слайд #11
Определение
Плоские углы ASB,BSC, CSA называются гранями трехгранного угла, их стороны – ребрами. Общая вершина Sплоских углов называется вершинойтрехгранного угла.
Плоские углы ASB,BSC, CSA называются гранями трехгранного угла, их стороны – ребрами. Общая вершина Sплоских углов называется вершинойтрехгранного угла.

Слайд #12
Трехгранный угол
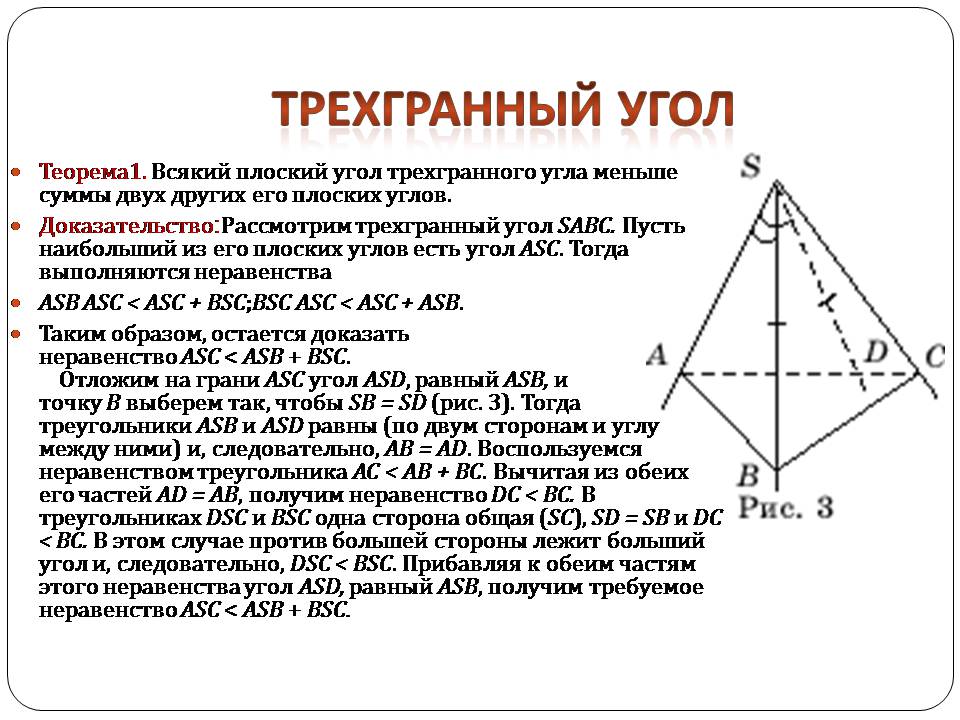
Теорема1. Всякий плоский угол трехгранного угла меньше суммы двух других его плоских углов.
Доказательство:Рассмотрим трехгранный угол SABC. Пусть наибольший из его плоских углов есть угол ASC. Тогда выполняются неравенства
ASB ASC < ASC + BSC;BSC ASC < ASC + ASB.
Таким образом, остается доказать неравенство ASС < ASB + BSC. Отложим на грани ASC угол ASD, равный ASB, и точку B выберем так, чтобы SB = SD (рис. 3). Тогда треугольники ASB и ASD равны (по двум сторонам и углу между ними) и, следовательно, AB = AD. Воспользуемся неравенством треугольника AC < AB + BC. Вычитая из обеих его частей AD = AB, получим неравенство DC < BC. В треугольниках DSC и BSC одна сторона общая (SC), SD = SB и DC < BC. В этом случае против большей стороны лежит больший угол и, следовательно, DSC < BSC. Прибавляя к обеим частям этого неравенства угол ASD, равный ASB, получим требуемое неравенство ASС < ASB + BSC.
Теорема1. Всякий плоский угол трехгранного угла меньше суммы двух других его плоских углов.
Доказательство:Рассмотрим трехгранный угол SABC. Пусть наибольший из его плоских углов есть угол ASC. Тогда выполняются неравенства
ASB ASC < ASC + BSC;BSC ASC < ASC + ASB.
Таким образом, остается доказать неравенство ASС < ASB + BSC. Отложим на грани ASC угол ASD, равный ASB, и точку B выберем так, чтобы SB = SD (рис. 3). Тогда треугольники ASB и ASD равны (по двум сторонам и углу между ними) и, следовательно, AB = AD. Воспользуемся неравенством треугольника AC < AB + BC. Вычитая из обеих его частей AD = AB, получим неравенство DC < BC. В треугольниках DSC и BSC одна сторона общая (SC), SD = SB и DC < BC. В этом случае против большей стороны лежит больший угол и, следовательно, DSC < BSC. Прибавляя к обеим частям этого неравенства угол ASD, равный ASB, получим требуемое неравенство ASС < ASB + BSC.
Слайд #13
Трехгранный угол
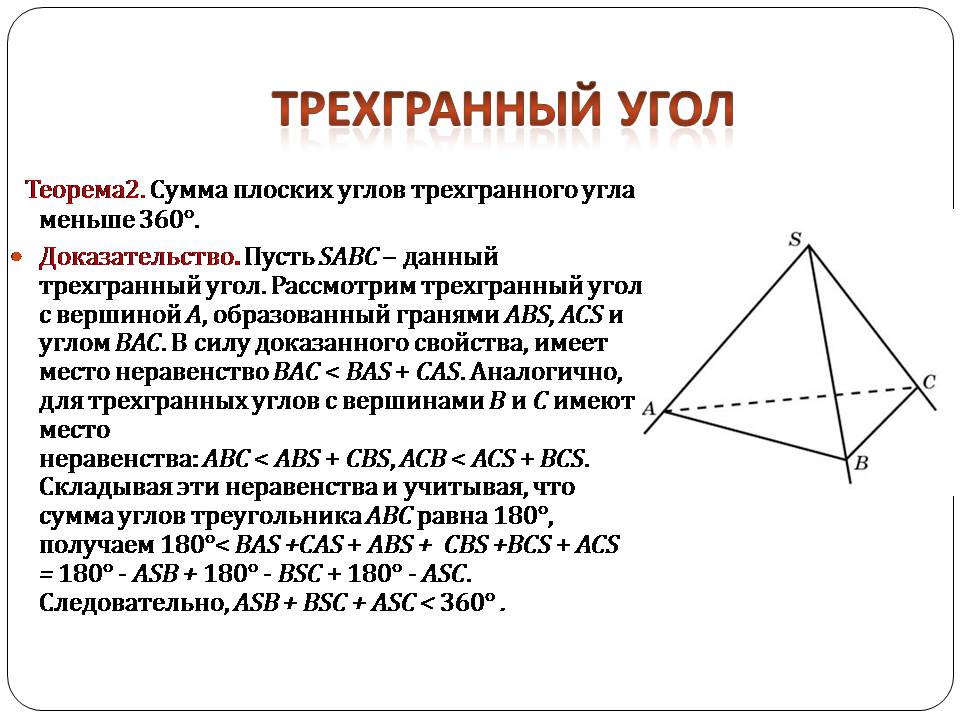
Теорема2. Сумма плоских углов трехгранного угла меньше 360°.
Доказательство. Пусть SABC – данный трехгранный угол. Рассмотрим трехгранный угол с вершиной A, образованный гранями ABS, ACS и углом BAC. В силу доказанного свойства, имеет место неравенство BAС < BAS + CAS. Аналогично, для трехгранных углов с вершинами B и С имеют место неравенства: ABС < ABS + CBS, ACB < ACS + BCS. Складывая эти неравенства и учитывая, что сумма углов треугольника ABC равна 180°, получаем 180°< BAS +CAS + ABS + CBS +BCS + ACS = 180° - ASB + 180° - BSC + 180° - ASC. Следовательно, ASB + BSC + ASC < 360° .
Теорема2. Сумма плоских углов трехгранного угла меньше 360°.
Доказательство. Пусть SABC – данный трехгранный угол. Рассмотрим трехгранный угол с вершиной A, образованный гранями ABS, ACS и углом BAC. В силу доказанного свойства, имеет место неравенство BAС < BAS + CAS. Аналогично, для трехгранных углов с вершинами B и С имеют место неравенства: ABС < ABS + CBS, ACB < ACS + BCS. Складывая эти неравенства и учитывая, что сумма углов треугольника ABC равна 180°, получаем 180°< BAS +CAS + ABS + CBS +BCS + ACS = 180° - ASB + 180° - BSC + 180° - ASC. Следовательно, ASB + BSC + ASC < 360° .
Слайд #14
Теорема 3
Каждый плоский угол многогранного угла меньше суммы всех остальных его плоских углов.
Каждый плоский угол многогранного угла меньше суммы всех остальных его плоских углов.

Слайд #15
Теорема косинусов для трехгранного угла
cos α = cos β cos γ + sin β sin γ cos A
где α, β, γ – плоские углы, A – двугранный угол, составленный плоскостями углов β и γ.
cos α = cos β cos γ + sin β sin γ cos A
где α, β, γ – плоские углы, A – двугранный угол, составленный плоскостями углов β и γ.

Слайд #16
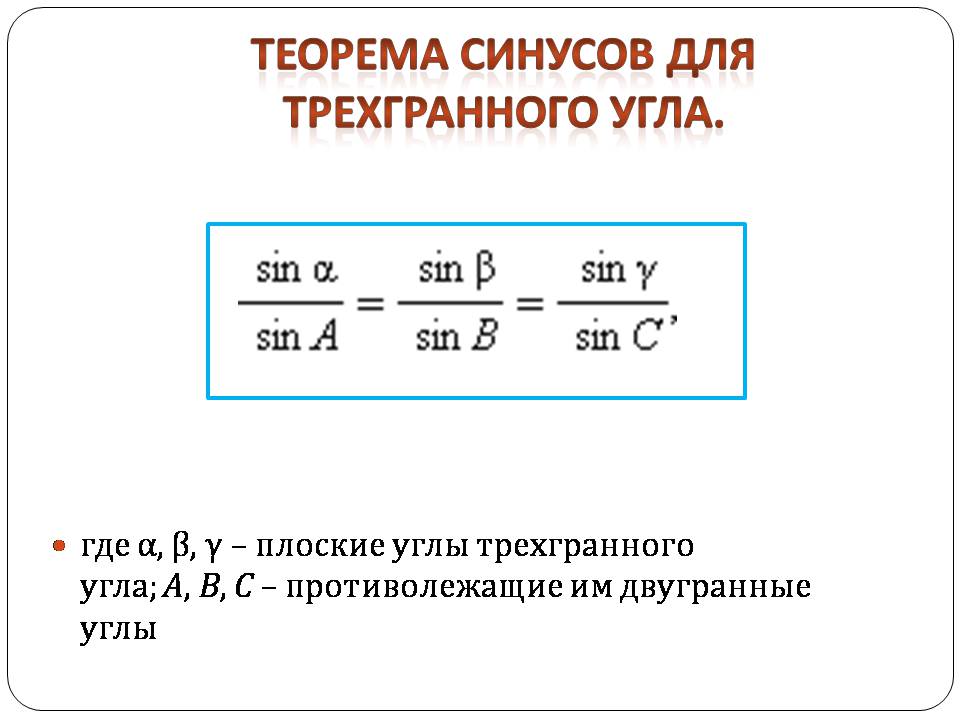
Теорема синусов для трехгранного угла.
где α, β, γ – плоские углы трехгранного угла; A, B, C – противолежащие им двугранные углы
где α, β, γ – плоские углы трехгранного угла; A, B, C – противолежащие им двугранные углы
Слайд #17
Измерение трехгранного угла
Опишем около его вершины S единичную сферу и обозначим точки пересечения ребер трехгранного угла с этой сферой A, B, C
Плоскости граней трехгранного угла разбивают эту сферу на шесть попарно равных сферических двуугольников, соответствующих двугранным углам данного трехгранного угла. Сферический треугольник ABC и симметричный ему сферический треугольник A'B'C' являются пересечением трех двуугольников. Поэтому удвоенная сумма двугранных углов равна 360° плюс учетверенная величина трехгранного угла, или
уголSAB +уголSB + уголSC = 180° + 2ÐSABC.
Опишем около его вершины S единичную сферу и обозначим точки пересечения ребер трехгранного угла с этой сферой A, B, C
Плоскости граней трехгранного угла разбивают эту сферу на шесть попарно равных сферических двуугольников, соответствующих двугранным углам данного трехгранного угла. Сферический треугольник ABC и симметричный ему сферический треугольник A'B'C' являются пересечением трех двуугольников. Поэтому удвоенная сумма двугранных углов равна 360° плюс учетверенная величина трехгранного угла, или
уголSAB +уголSB + уголSC = 180° + 2ÐSABC.

Слайд #18
Спасибо за внимание!

Слайд #19
Источники
http://school-collection.edu.ru/catalog/res/AFA328E0-1FC2-4471-9A20-9598EDB55FDF/view/
http://www.mathematics.ru/courses/stereometry/content/chapter4/section/paragraph4/theory.html#.VHTkt4usXLl
https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D1%91%D1%85%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D1%8B%D0%B9_%D1%83%D0%B3%D0%BE%D0%BB
http://geometry2006.narod.ru/Lecture/MnogUgly/MnogUgly.htm
http://school-collection.edu.ru/catalog/res/AFA328E0-1FC2-4471-9A20-9598EDB55FDF/view/
http://www.mathematics.ru/courses/stereometry/content/chapter4/section/paragraph4/theory.html#.VHTkt4usXLl
https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D1%91%D1%85%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D1%8B%D0%B9_%D1%83%D0%B3%D0%BE%D0%BB
http://geometry2006.narod.ru/Lecture/MnogUgly/MnogUgly.htm
