Презентація на тему «Інтеграли та їх застосування»
253
Слайд #1
Підготувала учениця 11-А класу
Інтеграли та їх застосування
Інтеграли та їх застосування
Слайд #2
Інтеграл виник з практичної потреби знаходити площі неплоских фігур. Найбільший внесок у вивченні інтегрального числення вніс Архімед.
Одного разу, прийшовши із рибалки, Архімед захотів визначити найбільш точно площу поверхні риби.
Одного разу, прийшовши із рибалки, Архімед захотів визначити найбільш точно площу поверхні риби.
Слайд #3
Розбивши поверхню риби на прямокутники, він знайшов їх площі, причому чим більшою була кількість прямокутників, тим точнішим було значення площі.
Слайд #4
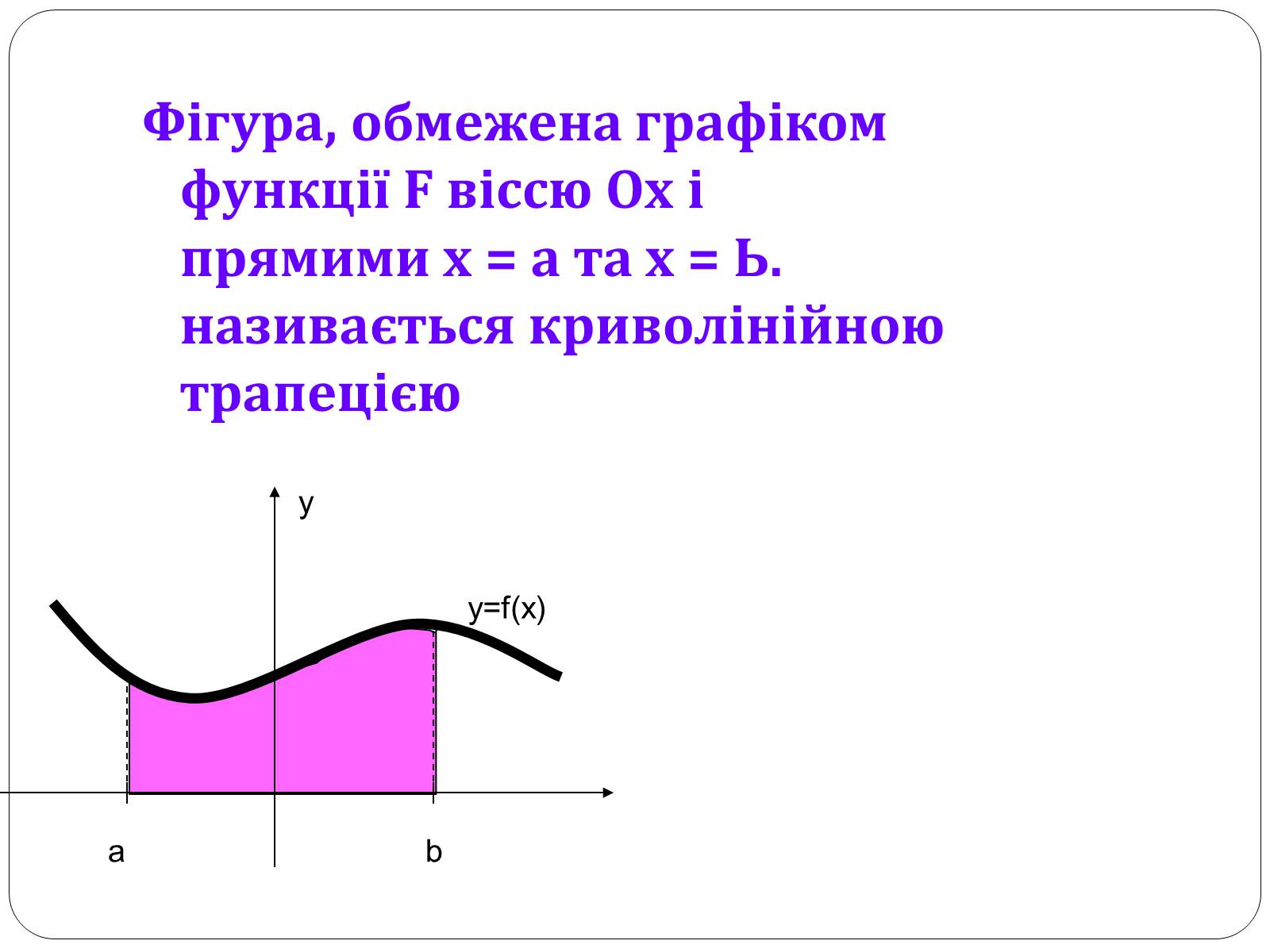
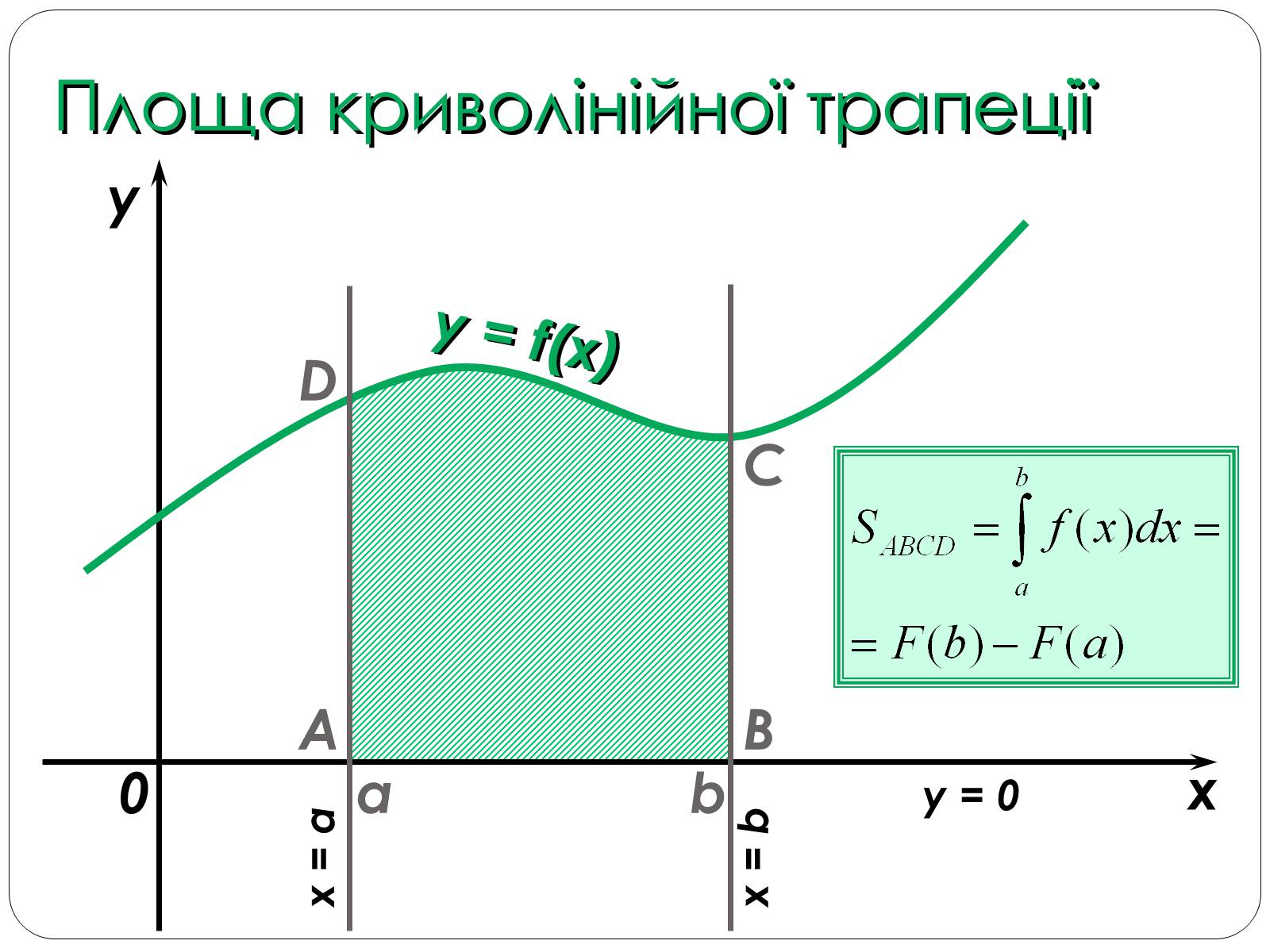
Фігура, обмежена графіком функції F віссю Ох і прямими х = а та х = Ь. називається криволінійною трапецією
a
b
y
y=f(x)
a
b
y
y=f(x)
Слайд #5
Теорема
Якщо f-неперервна
і невід'ємна на [а, b] функція, а F-її первісна на цьому відрізку, то площа S відповідної криволінійної трапеції дорівнює приросту первісної на відрізку [а, b], тобто S=F(b)-F(a)
Якщо f-неперервна
і невід'ємна на [а, b] функція, а F-її первісна на цьому відрізку, то площа S відповідної криволінійної трапеції дорівнює приросту первісної на відрізку [а, b], тобто S=F(b)-F(a)
Слайд #6
Числа а і в називають межами інтегрування:
а-нижня межу, в - верхня межа,
функцію у = f (х) - підінтегральна функція, вираз f (х) dх – підінтегральний вираз,
змінну х - змінною інтегрування
Таким чином
а-нижня межу, в - верхня межа,
функцію у = f (х) - підінтегральна функція, вираз f (х) dх – підінтегральний вираз,
змінну х - змінною інтегрування
Таким чином
Слайд #7
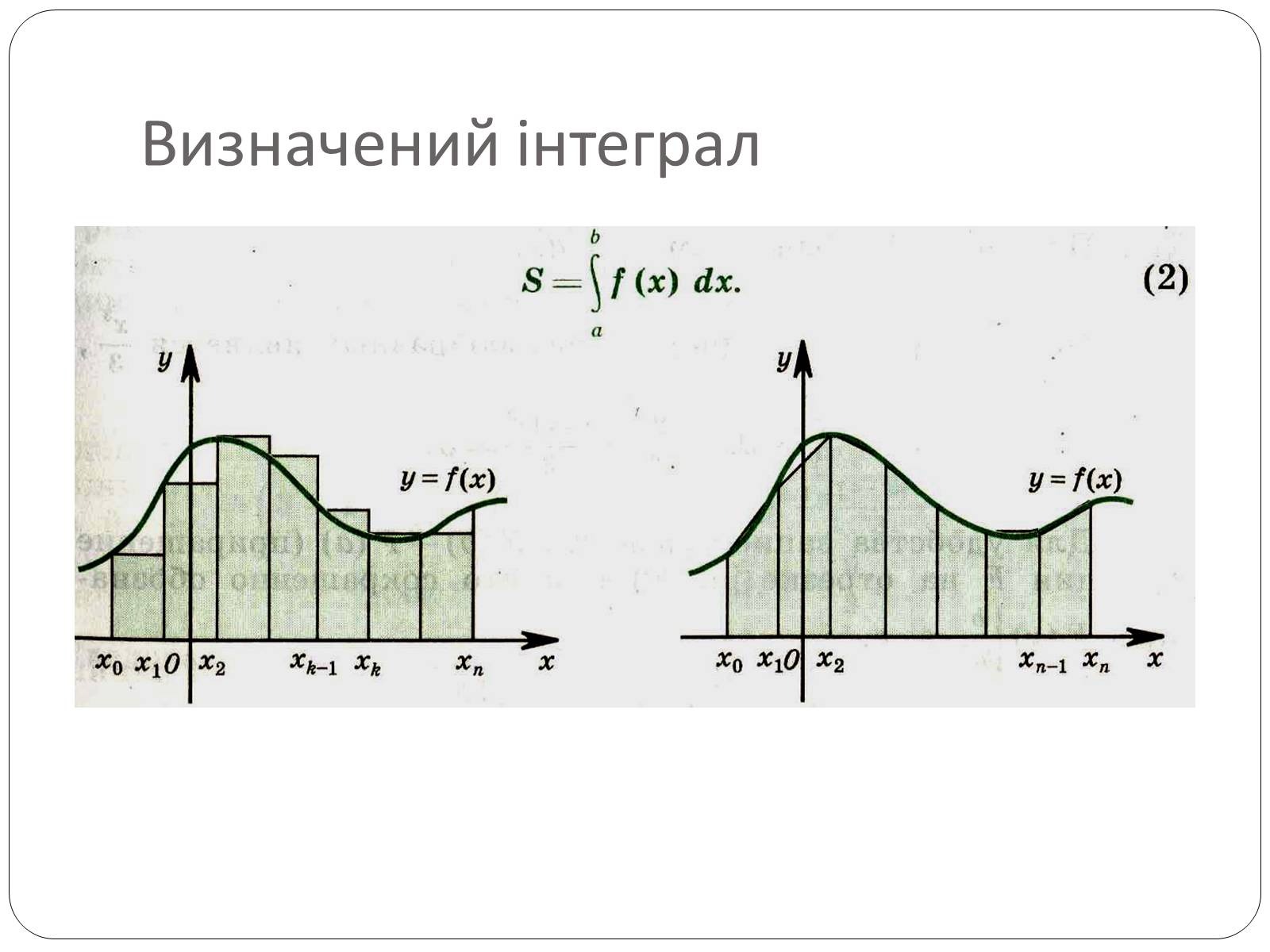
Визначений інтеграл
– формула Ньютона-Лейбніца.
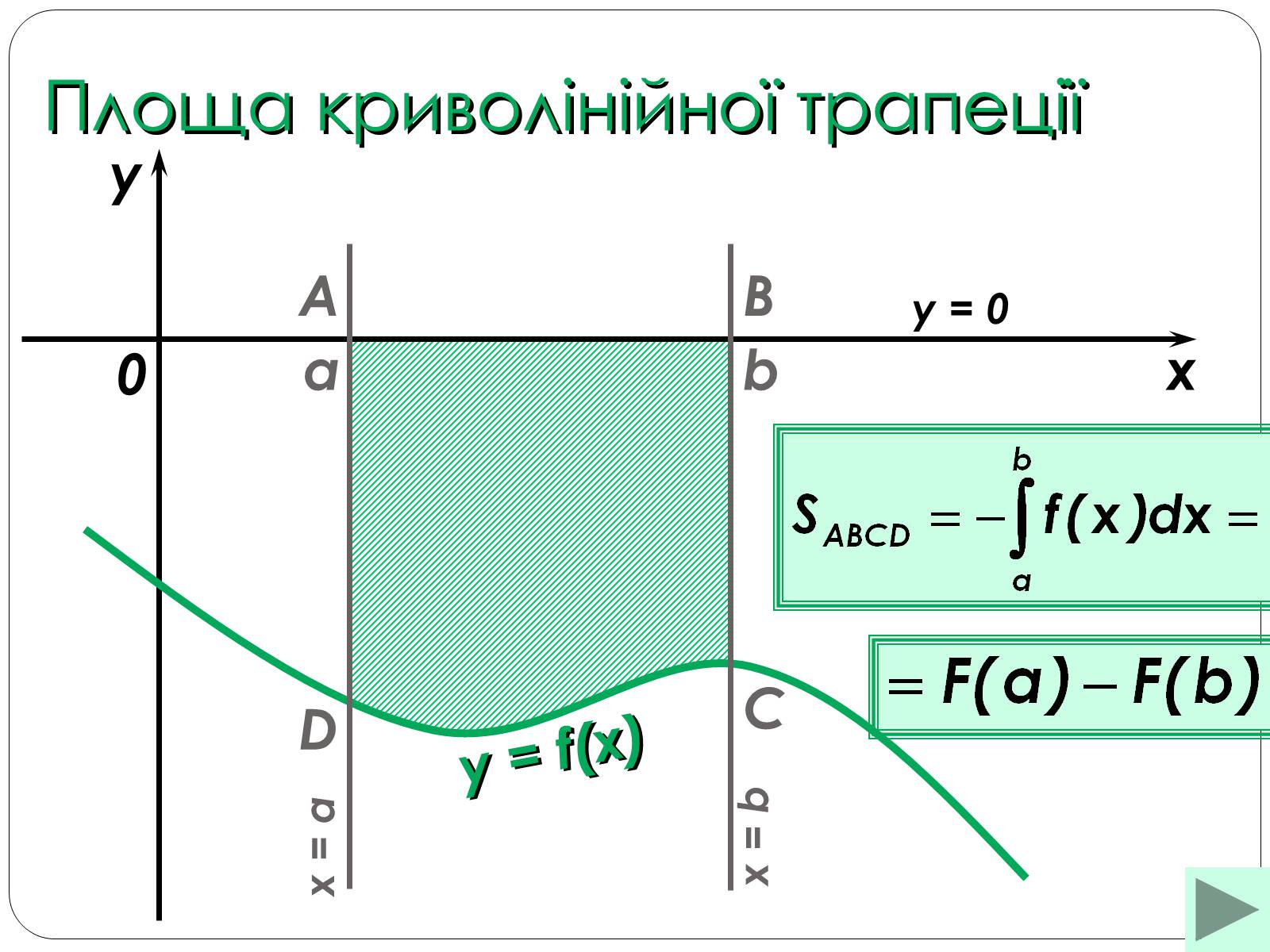
Геометричний зміст визначеного інтеграла полягає в тому, що визначений інтеграл дорівнює площі криволінійної трапеції, утвореної лініями:зверху обмеженою кривою у = f (х),і прямими у = 0, х = а, х = b.
– формула Ньютона-Лейбніца.
Геометричний зміст визначеного інтеграла полягає в тому, що визначений інтеграл дорівнює площі криволінійної трапеції, утвореної лініями:зверху обмеженою кривою у = f (х),і прямими у = 0, х = а, х = b.
Слайд #8
Визначений інтеграл
Слайд #9
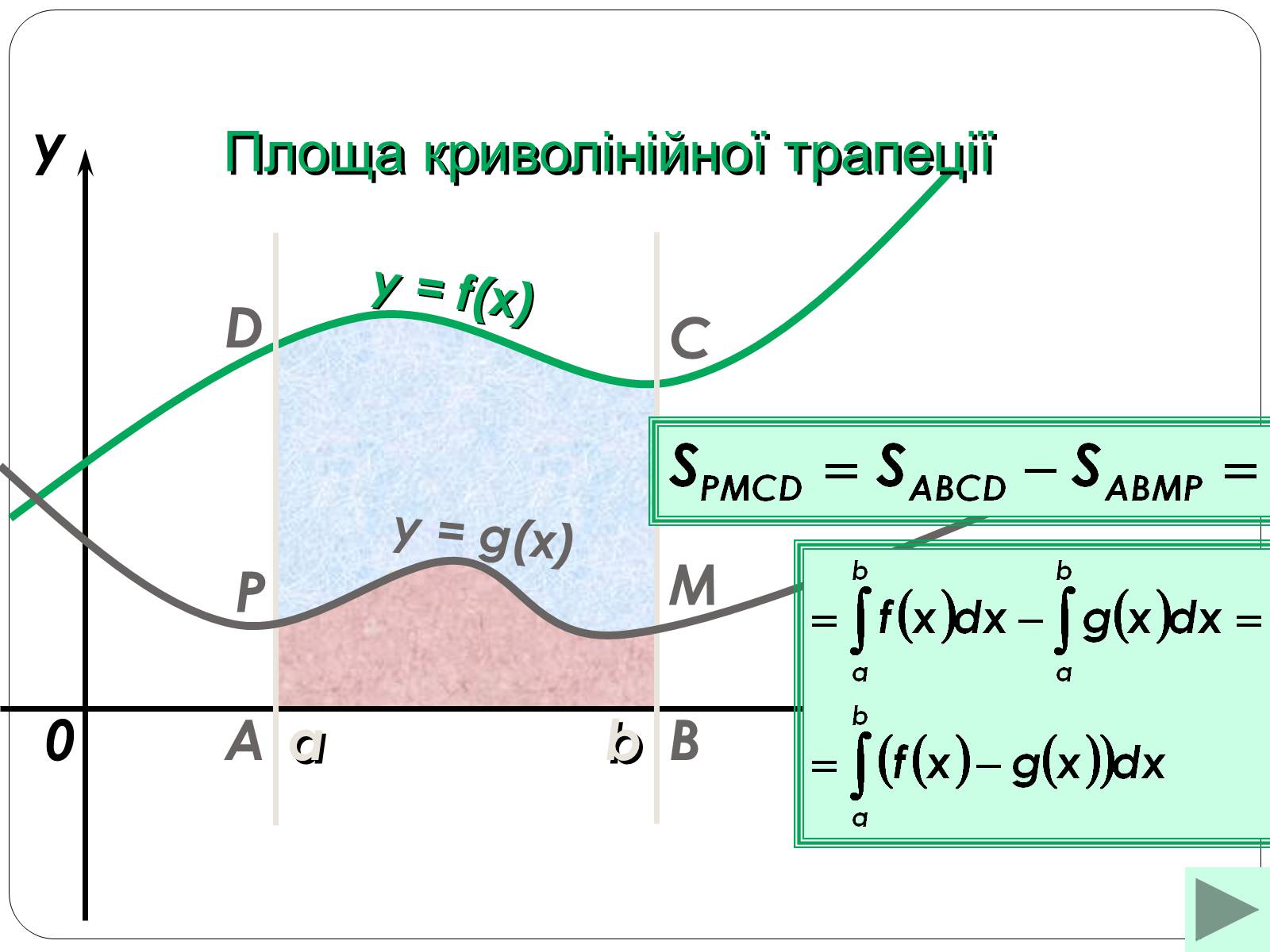
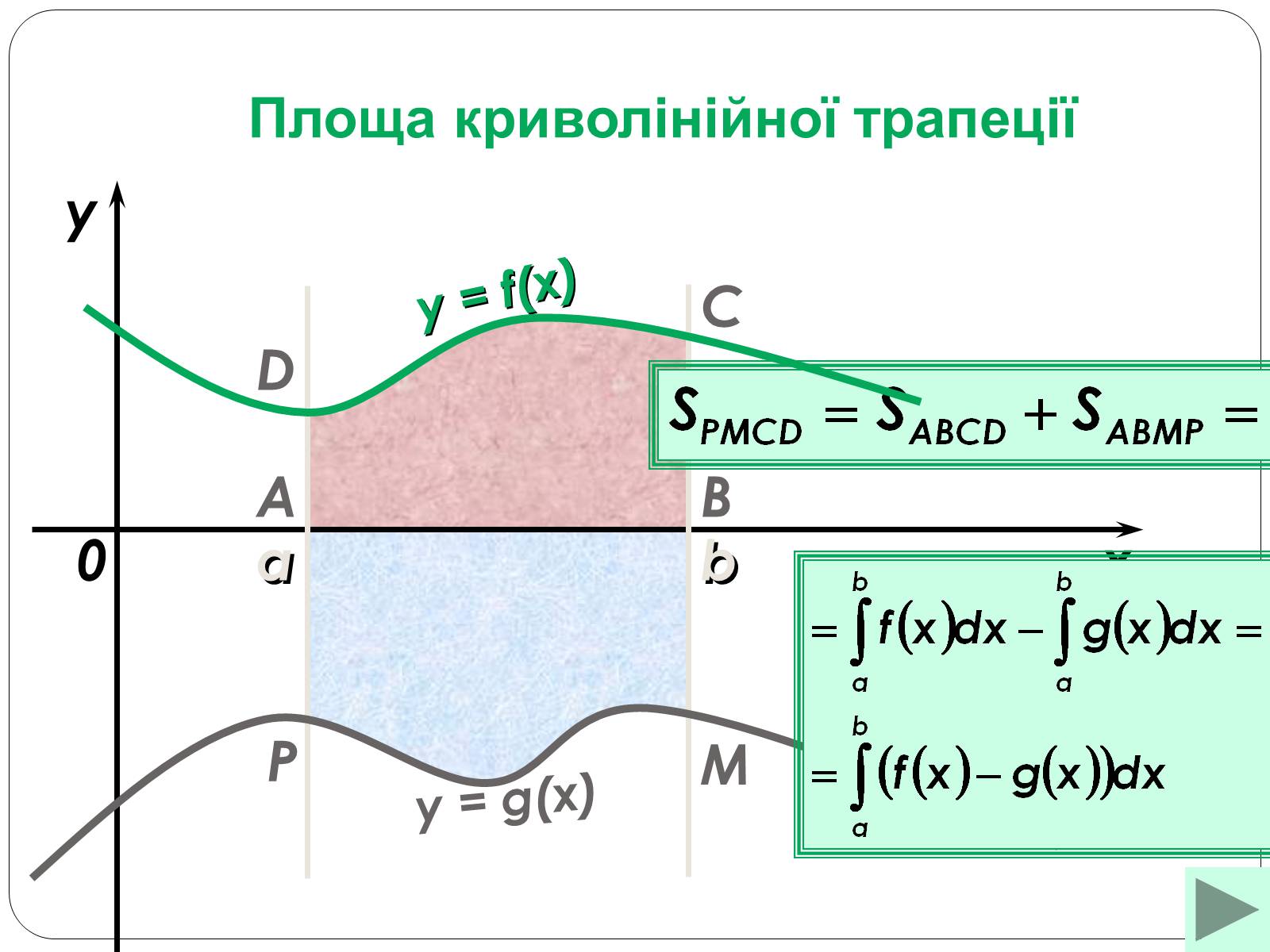
Знаходження площі криволінійної трапеції, обмеженої графіком ДВОХ НЕПЕРЕРВНИХ ФУНКЦІЙ
Існує багато випадків, ми роглянемо деякі з них
Існує багато випадків, ми роглянемо деякі з них
Слайд #10
Площа криволінійної трапеції
a
b
x
y
y = f(x)
A
B
C
D
x = a
x = b
y = 0
a
b
x
y
y = f(x)
A
B
C
D
x = a
x = b
y = 0
Слайд #11
Площа криволінійної трапеції
a
b
x
y
y = f(x)
A
B
C
D
x = a
x = b
y = 0
a
b
x
y
y = f(x)
A
B
C
D
x = a
x = b
y = 0
Слайд #12
a
b
x
y
y = f(x)
y = g(x)
A
B
C
D
M
P
Площа криволінійної трапеції
b
x
y
y = f(x)
y = g(x)
A
B
C
D
M
P
Площа криволінійної трапеції
Слайд #13
a
b
x
y
y = f(x)
y = g(x)
A
B
C
D
M
P
Площа криволінійної трапеції
b
x
y
y = f(x)
y = g(x)
A
B
C
D
M
P
Площа криволінійної трапеції
Слайд #14
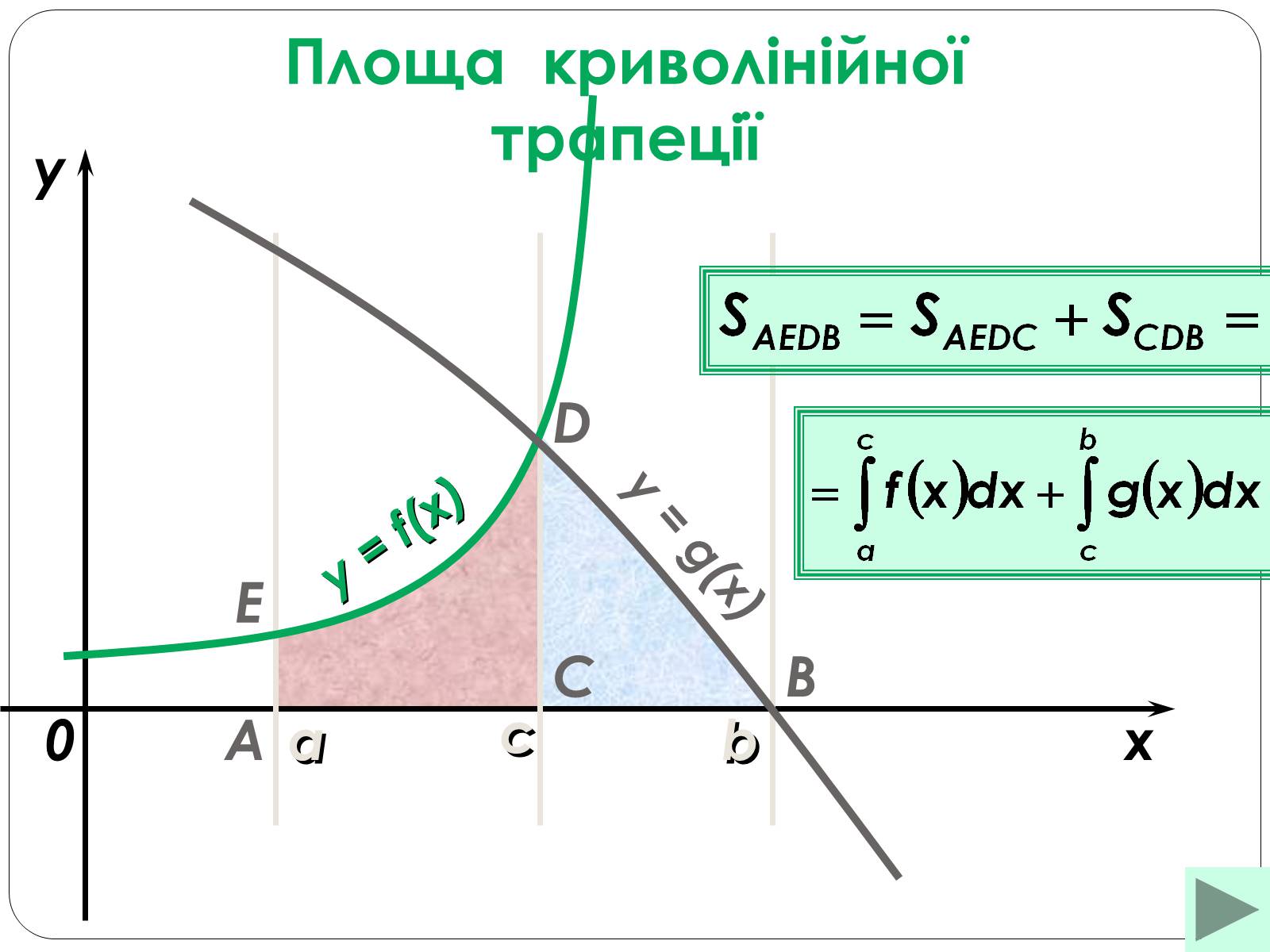
a
b
x
y
y = f(x)
y = g(x)
A
B
C
D
с
Е
Площа криволінійної трапеції
b
x
y
y = f(x)
y = g(x)
A
B
C
D
с
Е
Площа криволінійної трапеції
Слайд #15
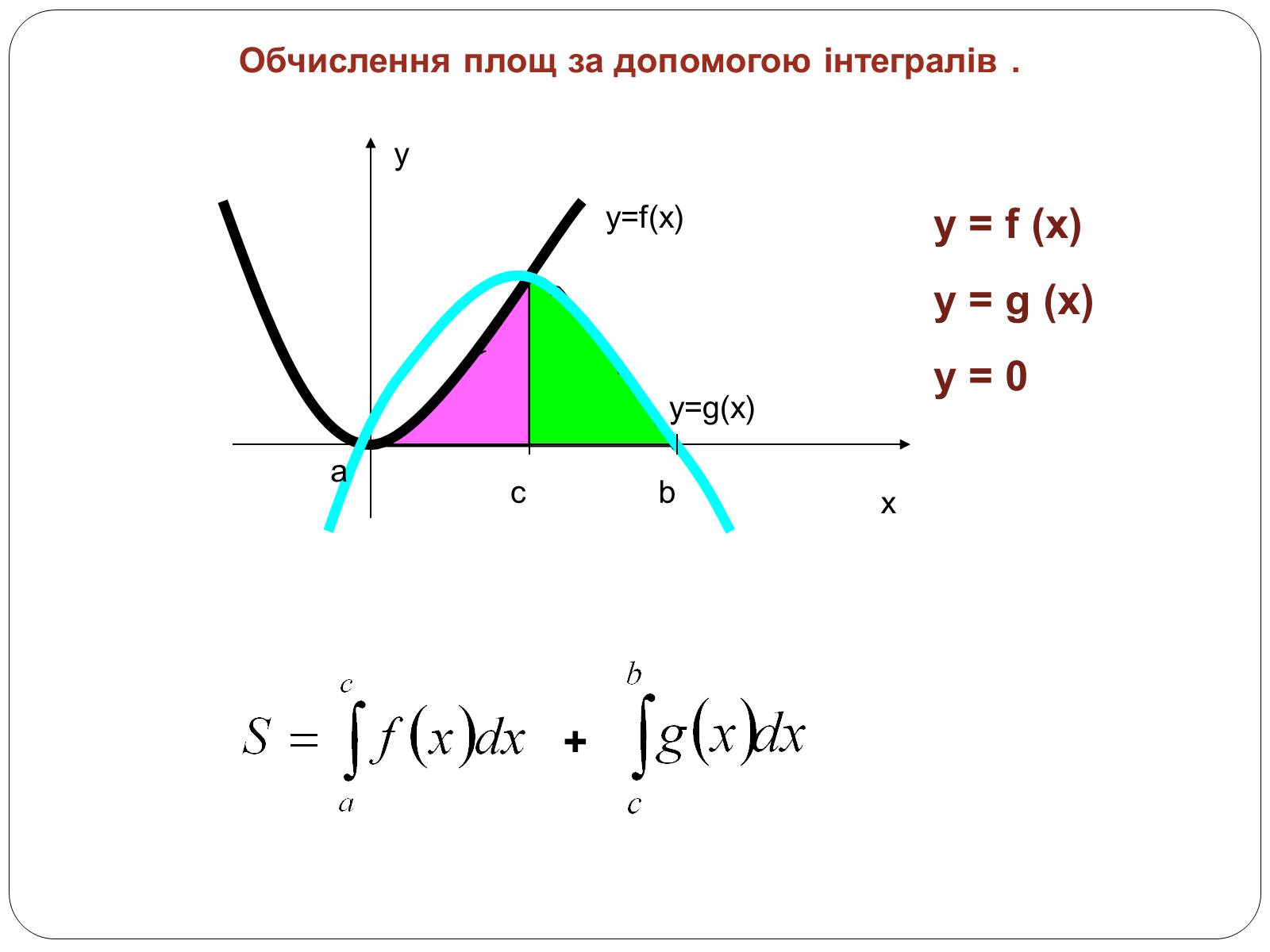
Обчислення площ за допомогою інтегралів .
y
x
y=f(x)
a
b
c
y=g(x)
+
y = f (x)
y = g (x)
y = 0
y
x
y=f(x)
a
b
c
y=g(x)
+
y = f (x)
y = g (x)
y = 0
Слайд #16
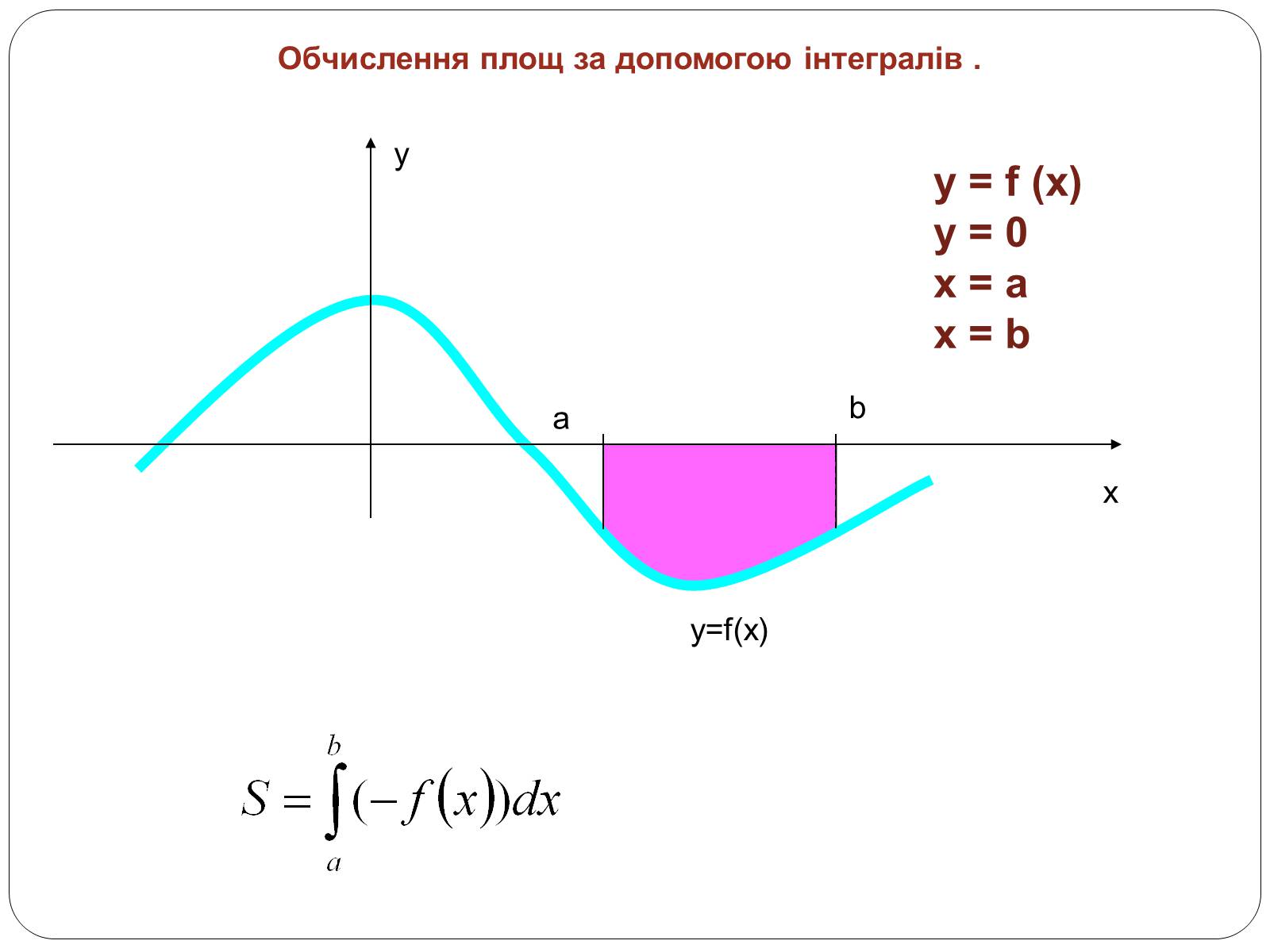
Обчислення площ за допомогою інтегралів .
y
x
y=f(x)
a
b
y = f (x)
y = 0
x = a
x = b
y
x
y=f(x)
a
b
y = f (x)
y = 0
x = a
x = b
Слайд #17
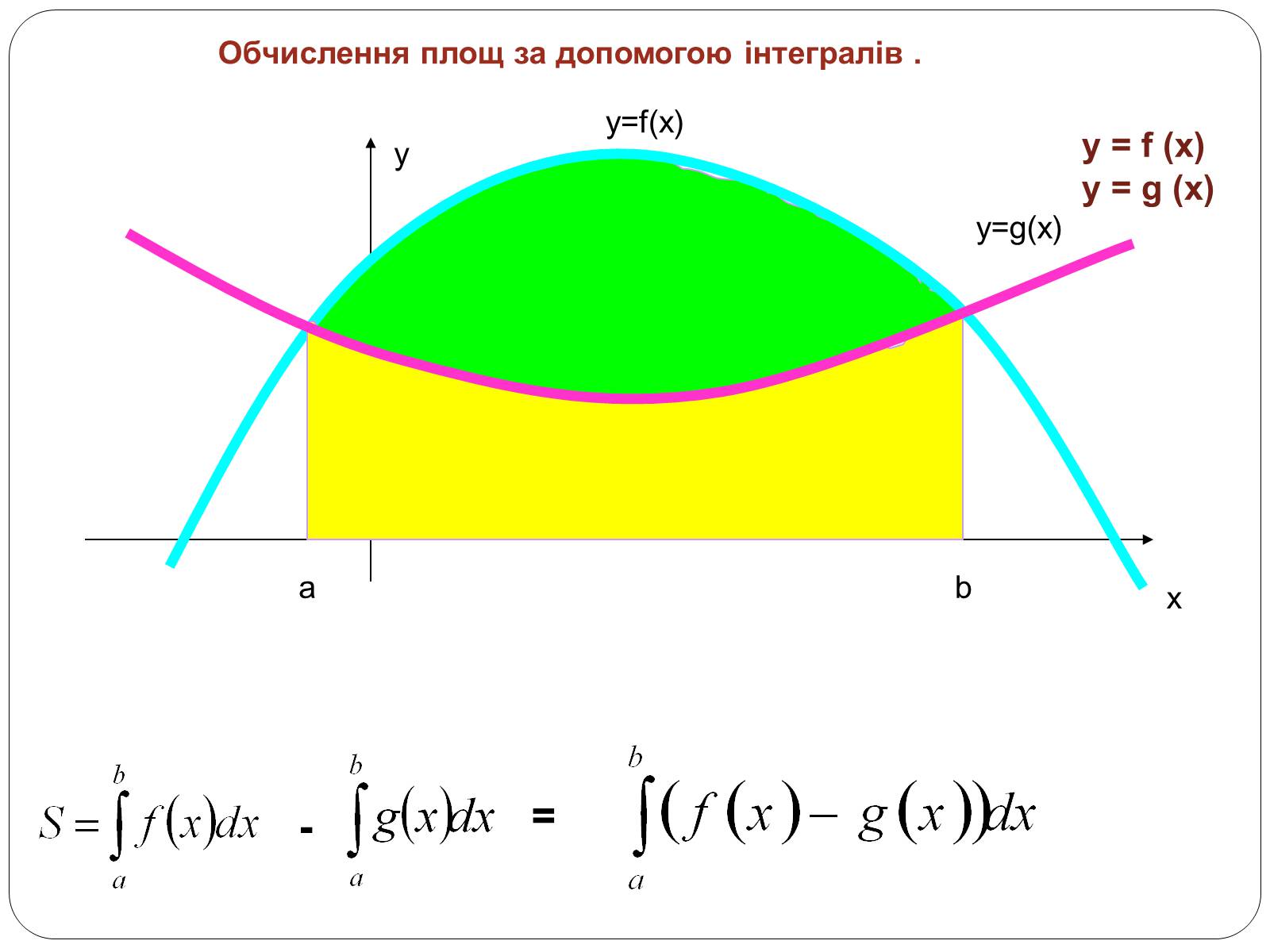
y
x
y=f(x)
a
b
y=g(x)
-
=
y = f (x)
y = g (x)
Обчислення площ за допомогою інтегралів .
x
y=f(x)
a
b
y=g(x)
-
=
y = f (x)
y = g (x)
Обчислення площ за допомогою інтегралів .
