Презентація на тему «Комбінації тіл»

Презентаціяна тему:
“Комбінації тіл”

Різні комбінації тіл

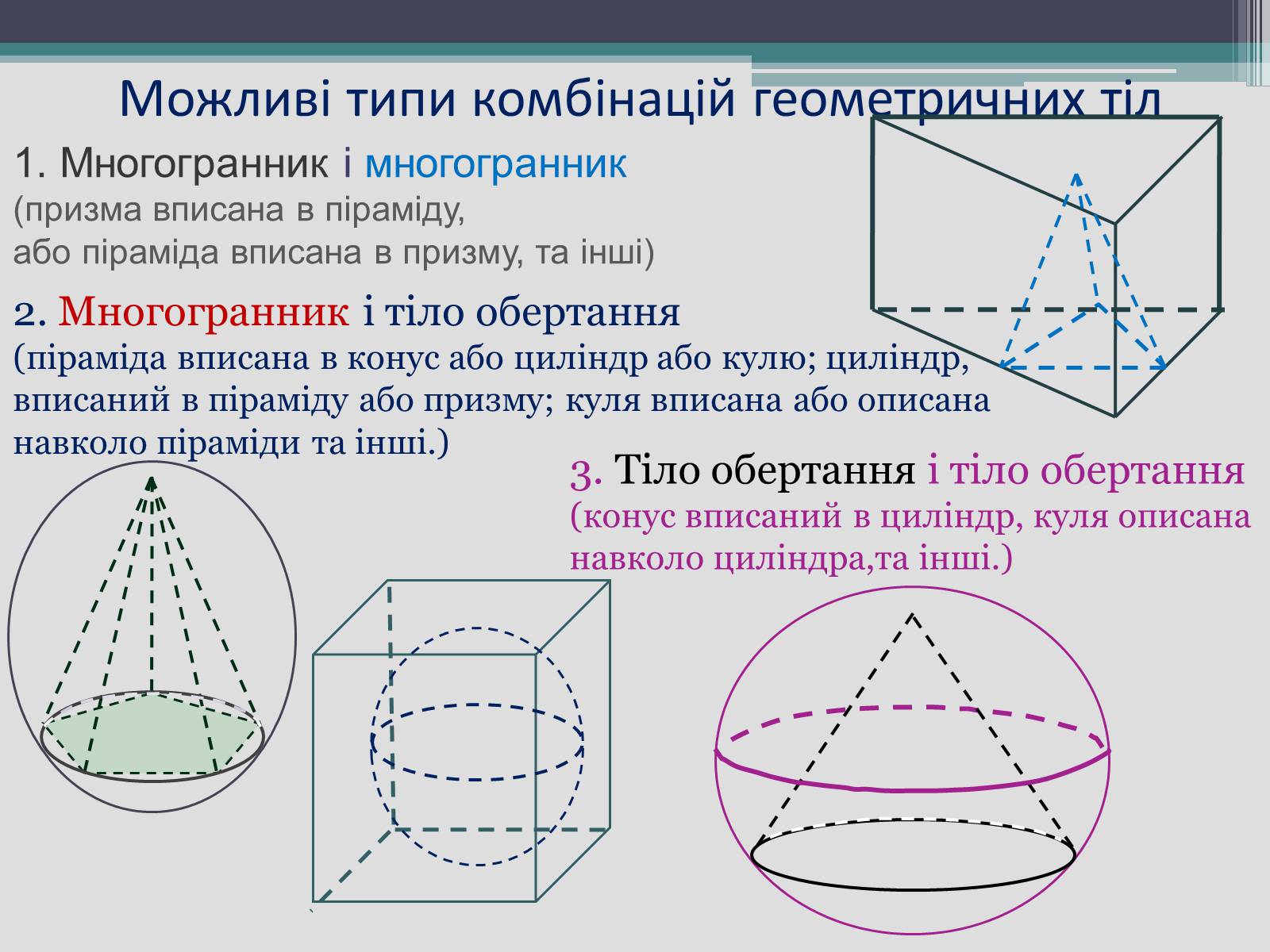
Можливі типи комбінацій геометричних тіл
1. Многогранник і многогранник (призма вписана в піраміду,
або піраміда вписана в призму, та інші)
2. Многогранник і тіло обертання
(піраміда вписана в конус або циліндр або кулю; циліндр, вписаний в піраміду або призму; куля вписана або описана навколо піраміди та інші.)
3. Тіло обертання і тіло обертання
(конус вписаний в циліндр, куля описана навколо циліндра,та інші.)

Циліндр, вписаний в призму
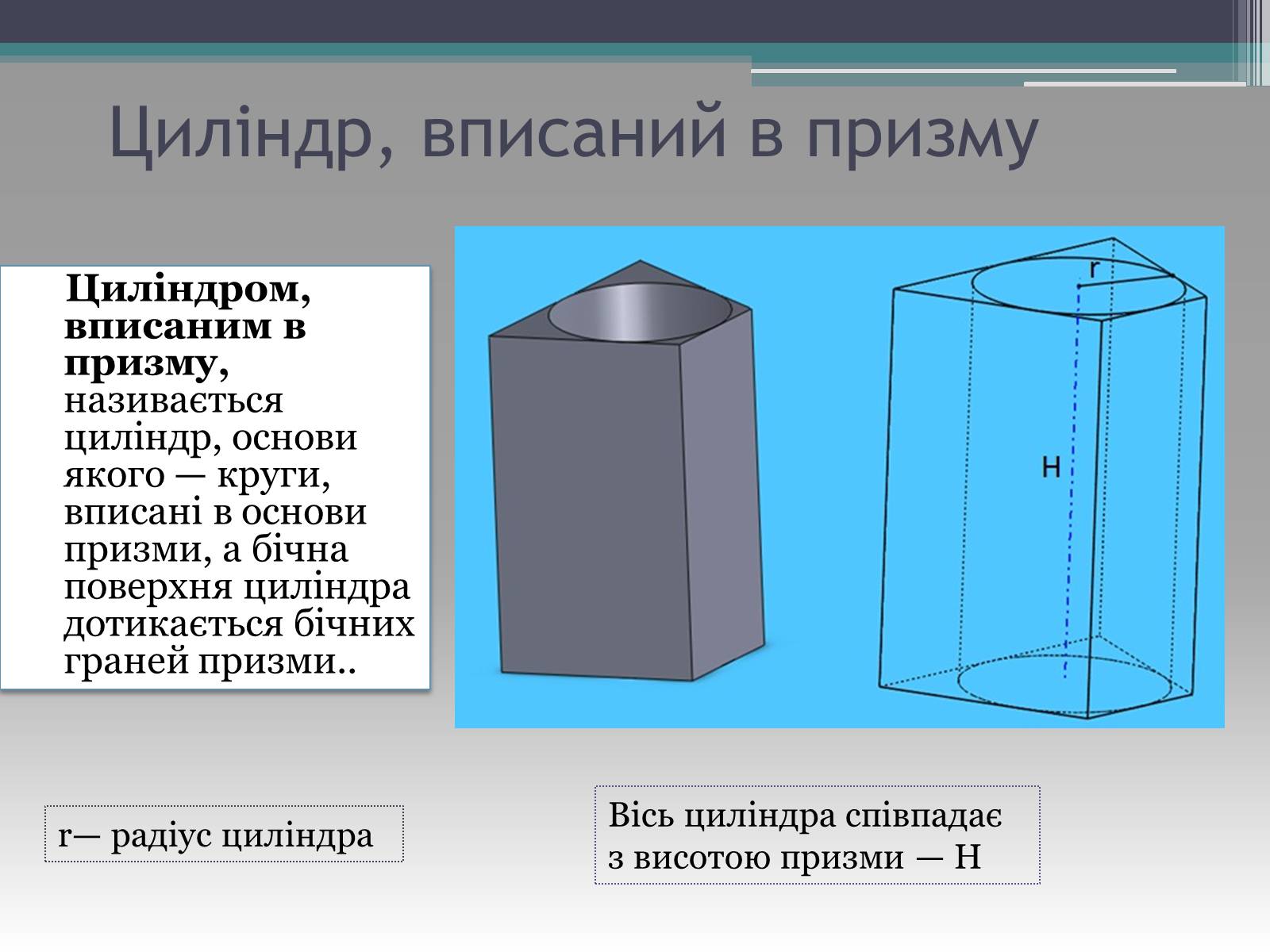
Циліндром, вписаним в призму, називається циліндр, основи якого — круги, вписані в основи призми, а бічна поверхня циліндра дотикається бічних граней призми..
r— радіус циліндра
Вісь циліндра співпадає з висотою призми — Н

Циліндр, описаний навколо призми
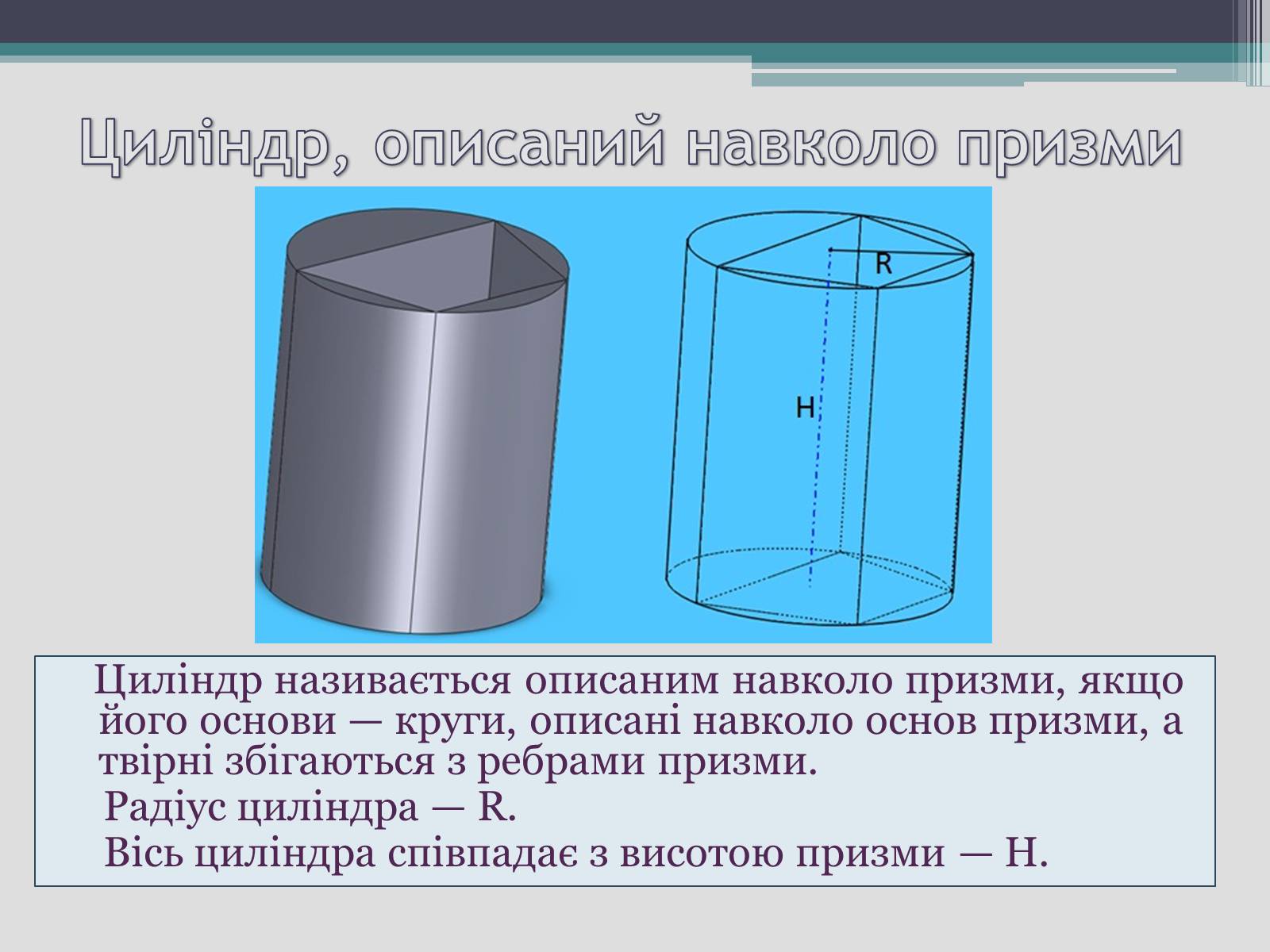
Циліндр називається описаним навколо призми, якщо його основи — круги, описані навколо основ призми, а твірні збігаються з ребрами призми.
Радіус циліндра — R.
Вісь циліндра співпадає з висотою призми — H.

Конус, вписаний в піраміду
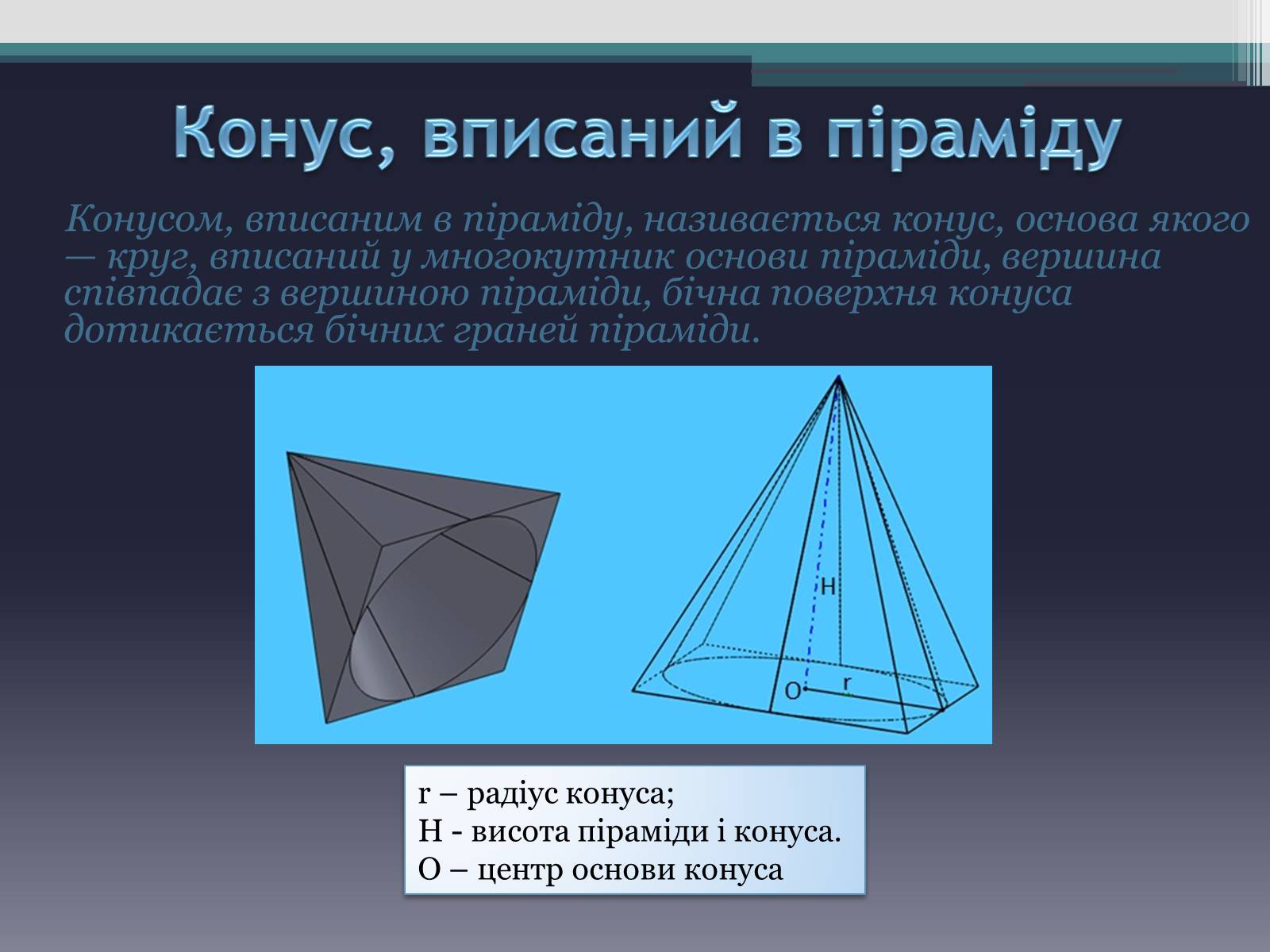
Конусом, вписаним в піраміду, називається конус, основа якого — круг, вписаний у многокутник основи піраміди, вершина співпадає з вершиною піраміди, бічна поверхня конуса дотикається бічних граней піраміди.
r – радіус конуса;
Н - висота піраміди і конуса.
О – центр основи конуса

Конус, описаний навколо піраміди
Конус називається описаним навколо піраміди, якщо його основа — круг, описаний навколо піраміди, вершина співпадає з вершиною піраміди, а твірні збігаються з ребрами піраміди. Висоти конуса і піраміди збігаються на основі єдності прямої, перпендикулярної до площини і проведеної через точку, яка не лежить у даній площині. Радіус вписаного в основу піраміди кола (круга) перпендикулярний стороні многокутника, який лежить в основі піраміди, і є проекцією твірної конуса на площину основи.
R – радіус конуса
Н - висота піраміди і конуса.
О – центр основи конуса

Куля, вписана в многогранник
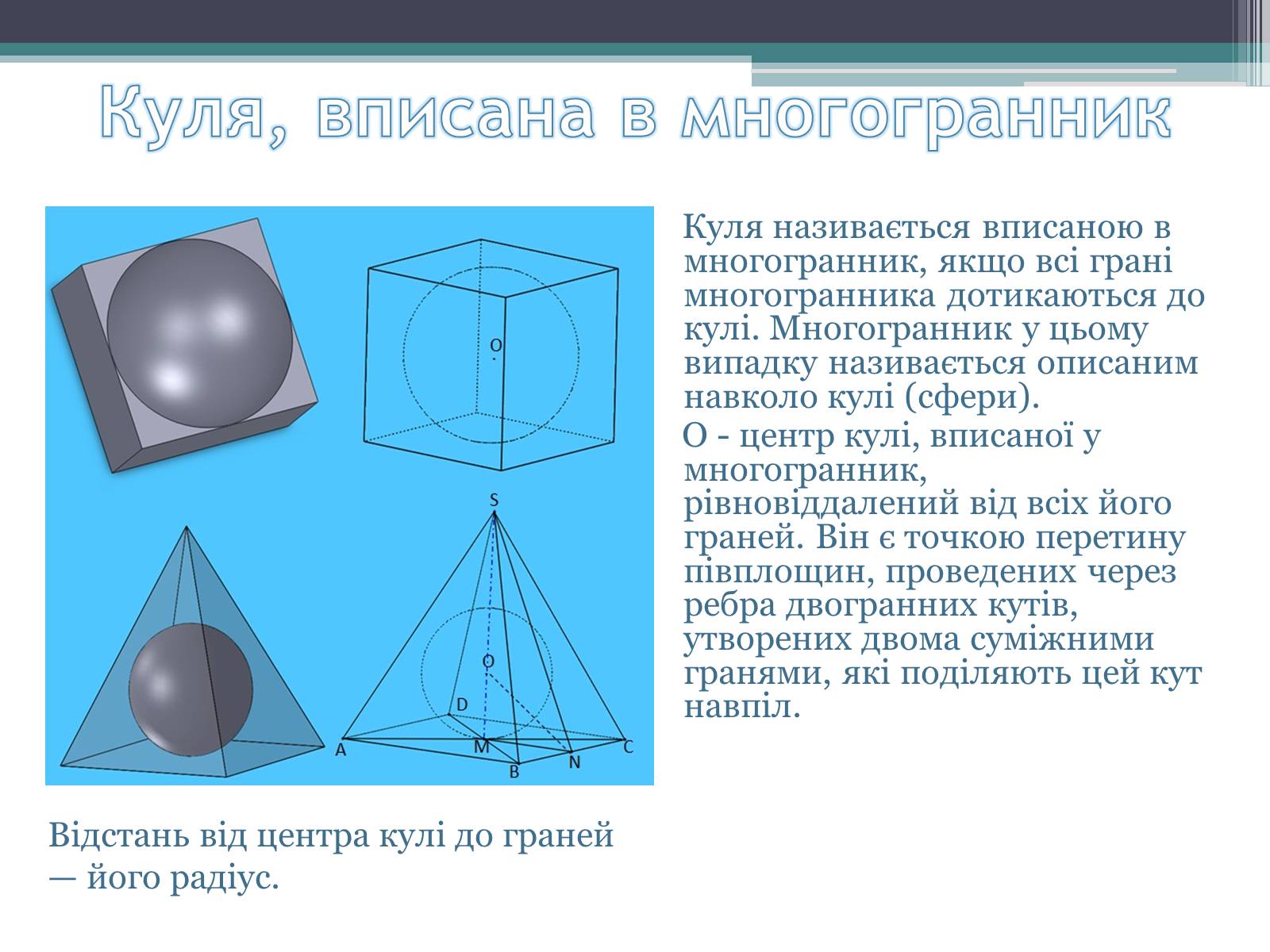
Куля називається вписаною в многогранник, якщо всі грані многогранника дотикаються до кулі. Многогранник у цьому випадку називається описаним навколо кулі (сфери).
О - центр кулі, вписаної у многогранник, рівновіддалений від всіх його граней. Він є точкою перетину півплощин, проведених через ребра двогранних кутів, утворених двома суміжними гранями, які поділяють цей кут навпіл.
Відстань від центра кулі до граней — його радіус.

Куля, описана навколо многогранника
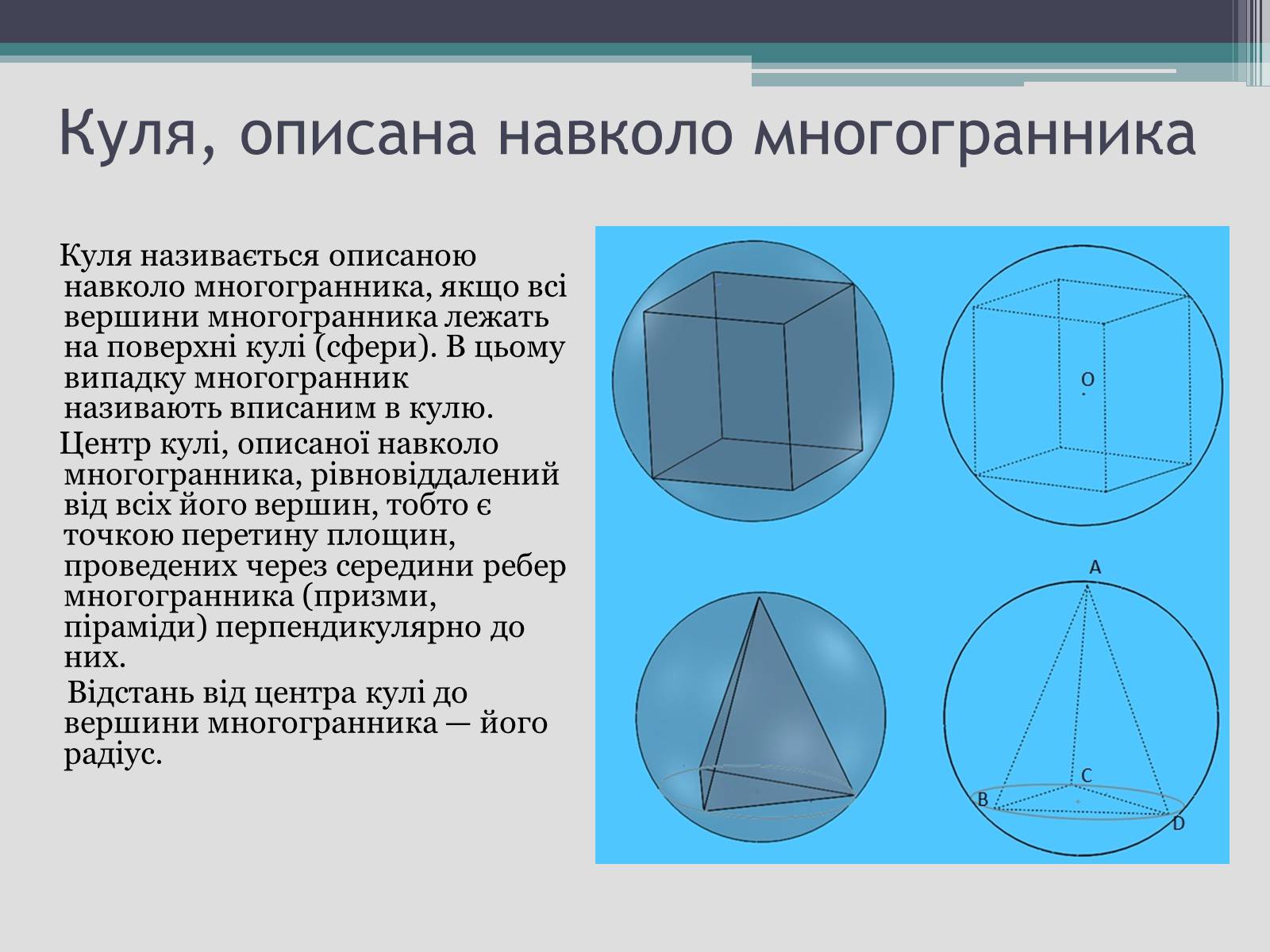
Куля називається описаною навколо многогранника, якщо всі вершини многогранника лежать на поверхні кулі (сфери). В цьому випадку многогранник називають вписаним в кулю.
Центр кулі, описаної навколо многогранника, рівновіддалений від всіх його вершин, тобто є точкою перетину площин, проведених через середини ребер многогранника (призми, піраміди) перпендикулярно до них.
Відстань від центра кулі до вершини многогранника — його радіус.

Куля, описана навколо призми
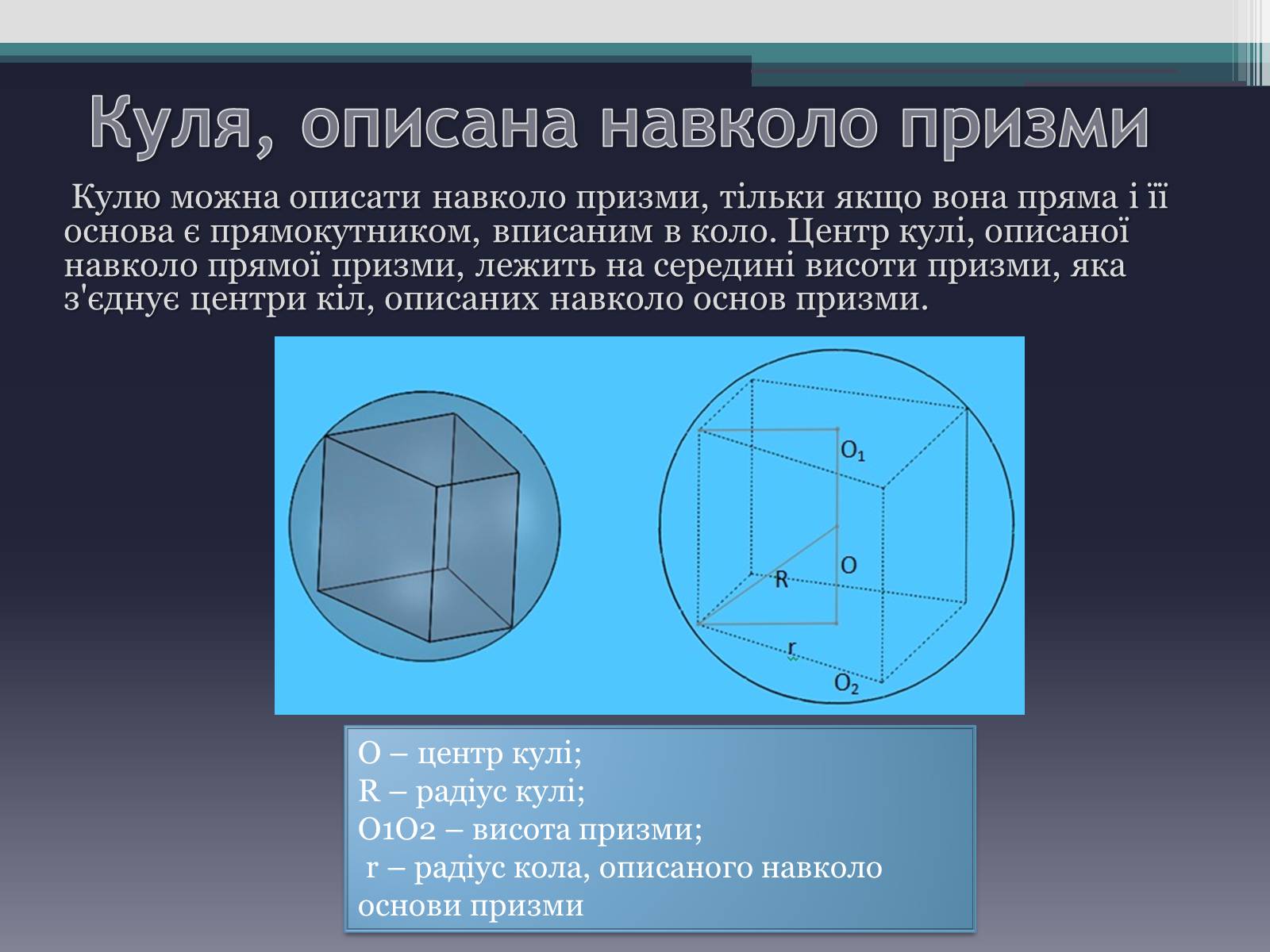
Кулю можна описати навколо призми, тільки якщо вона пряма і її основа є прямокутником, вписаним в коло. Центр кулі, описаної навколо прямої призми, лежить на середині висоти призми, яка з'єднує центри кіл, описаних навколо основ призми.
O – центр кулі;
R – радіус кулі;
O1O2 – висота призми;
r – радіус кола, описаного навколо основи призми

Куля, вписана в пряму призму
Кулю можна вписати в пряму призму, якщо її основи є многокутниками, описаними навколо кола, а висота призми дорівнює діаметру кулі і діаметру цього кола. Центр кулі, вписаної в пряму призму, лежить на середині відрізка, який з'єднує центри кіл, вписаних в основи призми. Причому, радіус кулі дорівнює радіусу кола, вписаного в основу призми, а діаметр кулі дорівнює висоті призми.
O – центр кулі;
R – радіус кулі;
O1O2 – висота призми і діаметр кулі;
r – радіус кола, вписаного в основу призми;
R=r=H/2.

Куля, описана навколо піраміди
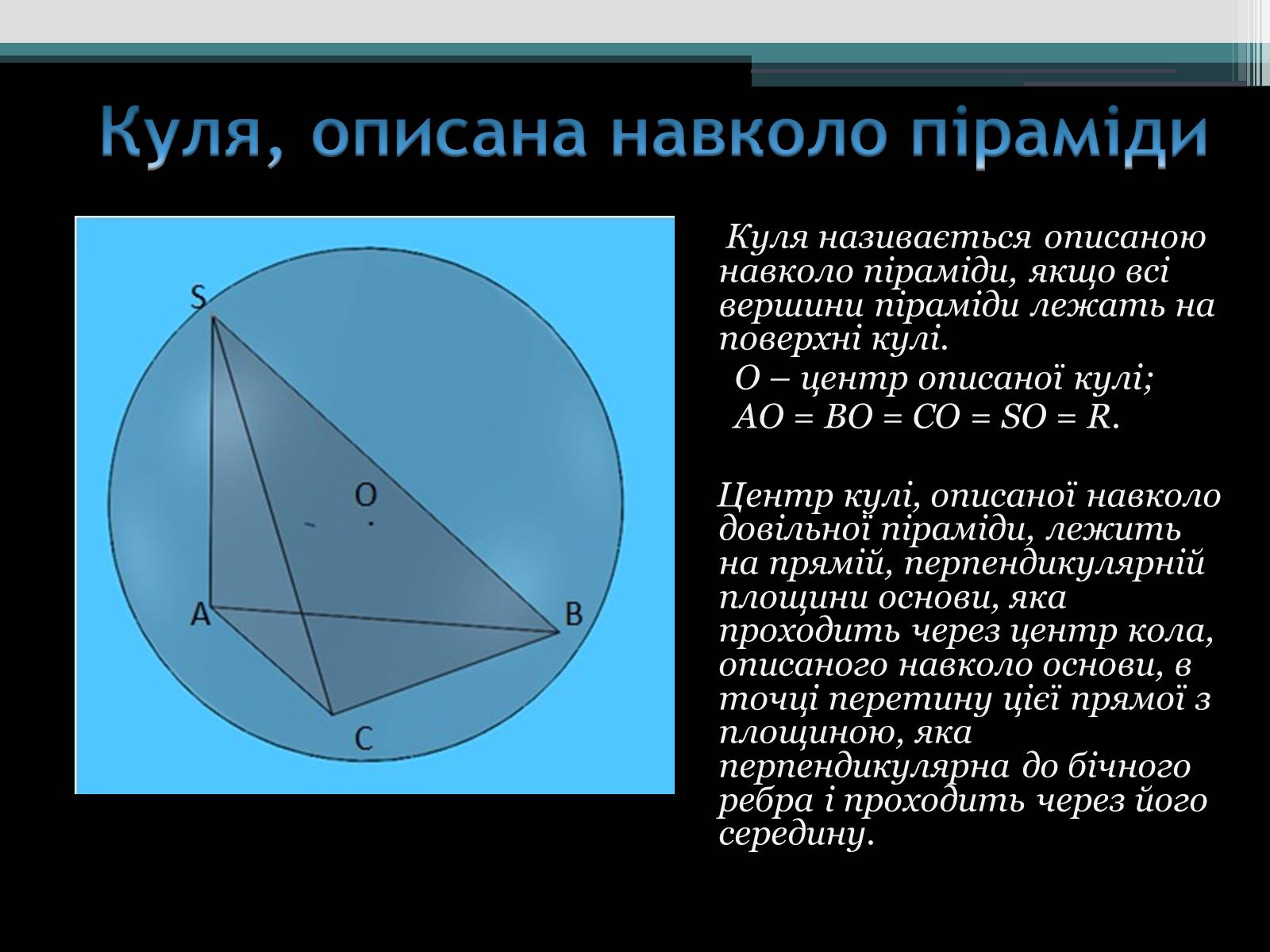
Куля називається описаною навколо піраміди, якщо всі вершини піраміди лежать на поверхні кулі.
O – центр описаної кулі;
AO = BO = CO = SO = R.
Центр кулі, описаної навколо довільної піраміди, лежить на прямій, перпендикулярній площини основи, яка проходить через центр кола, описаного навколо основи, в точці перетину цієї прямої з площиною, яка перпендикулярна до бічного ребра і проходить через його середину.

Куля, вписана в піраміду
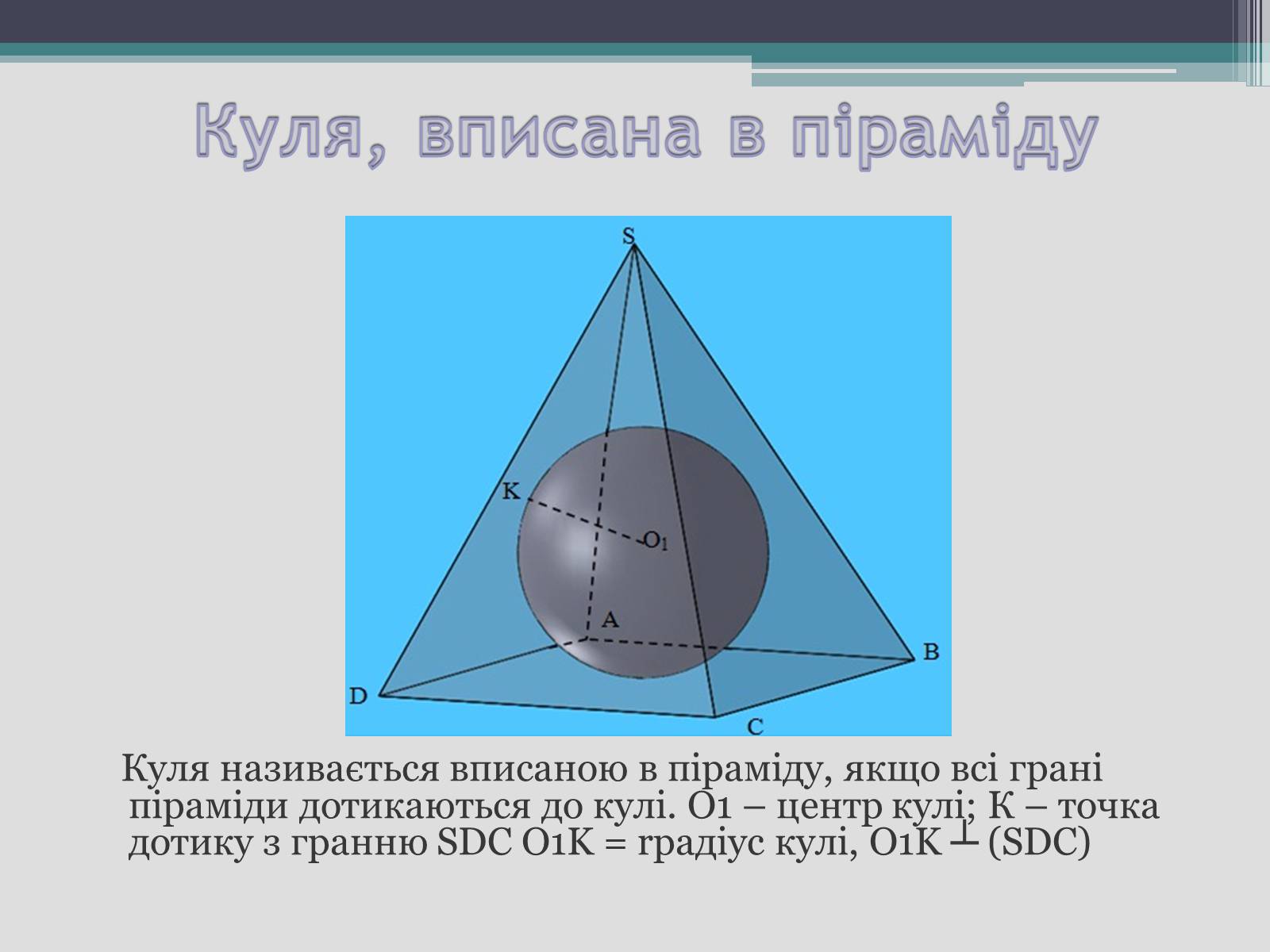
Куля називається вписаною в піраміду, якщо всі грані піраміди дотикаються до кулі. O1 – центр кулі; К – точка дотику з гранню SDC O1K = rрадіус кулі, O1K ┴ (SDC)

Комбінації тіл в навколишньому середовищі

Дякую за увагу!