Презентація на тему «Правильні многогранники» (варіант 3)
265
Слайд #1
Правильні многогранники
Слайд #2
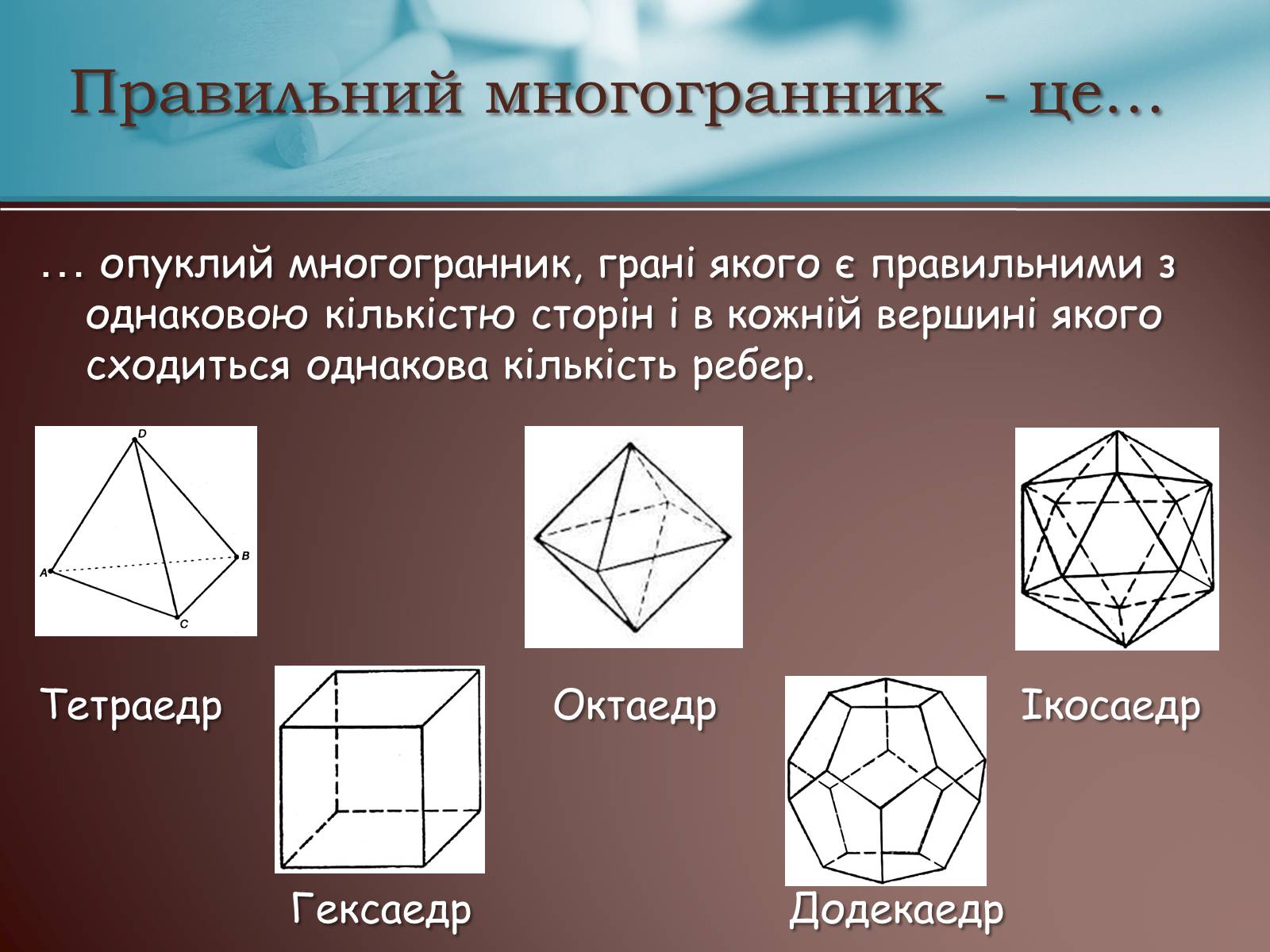
Правильний многогранник - це…
… опуклий многогранник, грані якого є правильними з однаковою кількістю сторін і в кожній вершині якого сходиться однакова кількість ребер.
Тетраедр Октаедр Ікосаедр
Гексаедр Додекаедр
… опуклий многогранник, грані якого є правильними з однаковою кількістю сторін і в кожній вершині якого сходиться однакова кількість ребер.
Тетраедр Октаедр Ікосаедр
Гексаедр Додекаедр
Слайд #3
Назва многогранника
I частина II частина
“тетра”-4
“гекса”-6 “едра”- грань
“окта”-8
“додека”-12
“ікоса”-20
I частина II частина
“тетра”-4
“гекса”-6 “едра”- грань
“окта”-8
“додека”-12
“ікоса”-20
Слайд #4
Платонові тіла
вогонь тетраедр
вода ікосаедр
повітря октаедр
земля гексаедр
всесвіт додекаедр
вогонь тетраедр
вода ікосаедр
повітря октаедр
земля гексаедр
всесвіт додекаедр
Слайд #5
Правильний тетраедр
складений з чотирьох рівносторонніх трикутників;
кожна його вершина є вершиною трьох трикутників.
Отже, сума плоских кутів при кожній вершині дорівнює 180
складений з чотирьох рівносторонніх трикутників;
кожна його вершина є вершиною трьох трикутників.
Отже, сума плоских кутів при кожній вершині дорівнює 180
Слайд #6
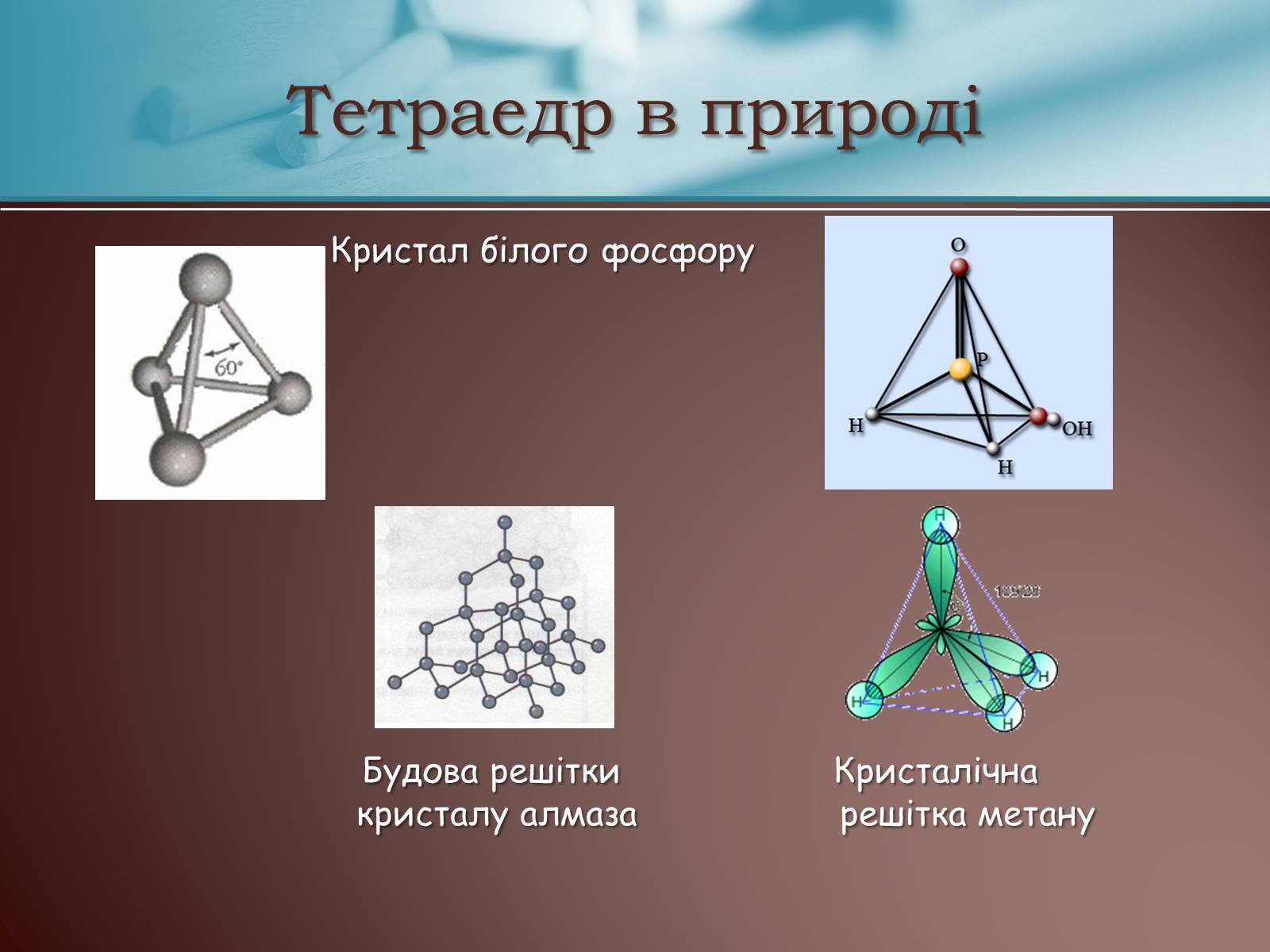
Кристал білого фосфору
Будова решітки Кристалічна кристалу алмаза решітка метану
Тетраедр в природі
Будова решітки Кристалічна кристалу алмаза решітка метану
Тетраедр в природі
Слайд #7
Правильний октаедр
складений з восьми рівносторонніх трикутників;
кожна вершина октаедра є вершиною чотирьох трикутників;
Отже, сума плоских кутів при кожній вершині 240.
складений з восьми рівносторонніх трикутників;
кожна вершина октаедра є вершиною чотирьох трикутників;
Отже, сума плоских кутів при кожній вершині 240.
Слайд #8
Вуглець С характеризується структурою октаедра
Октаедр в природі
Октаедр в природі
Слайд #9
Правильний ікосаедр
складений з дванадцяти рівносторонніх трикутників;
кожна вершина ікосаедра є вершиною п'яти трикутників.
Отже, сума плоских кутів при кожній вершині рівна 300.
складений з дванадцяти рівносторонніх трикутників;
кожна вершина ікосаедра є вершиною п'яти трикутників.
Отже, сума плоских кутів при кожній вершині рівна 300.
Слайд #10
Кристал бору має форму ікасаедра
У біології німецький біолог початку ХХ століття Еге Геккель дослідив,що одноклітинні організми – феодарії, точно передають форму ікосаедра
У фізиці капсиди багатьох вірусів (наприклад бактеріофаги, мімівірус)
Ікосаедр в природі
У біології німецький біолог початку ХХ століття Еге Геккель дослідив,що одноклітинні організми – феодарії, точно передають форму ікосаедра
У фізиці капсиди багатьох вірусів (наприклад бактеріофаги, мімівірус)
Ікосаедр в природі
Слайд #11
Правильний гексаедр
складений з шести квадратів;
кожна вершина куба є вершиною трьох квадратів.
Отже, сума плоских кутів при кожній вершині рівна 270.
складений з шести квадратів;
кожна вершина куба є вершиною трьох квадратів.
Отже, сума плоских кутів при кожній вершині рівна 270.
Слайд #12
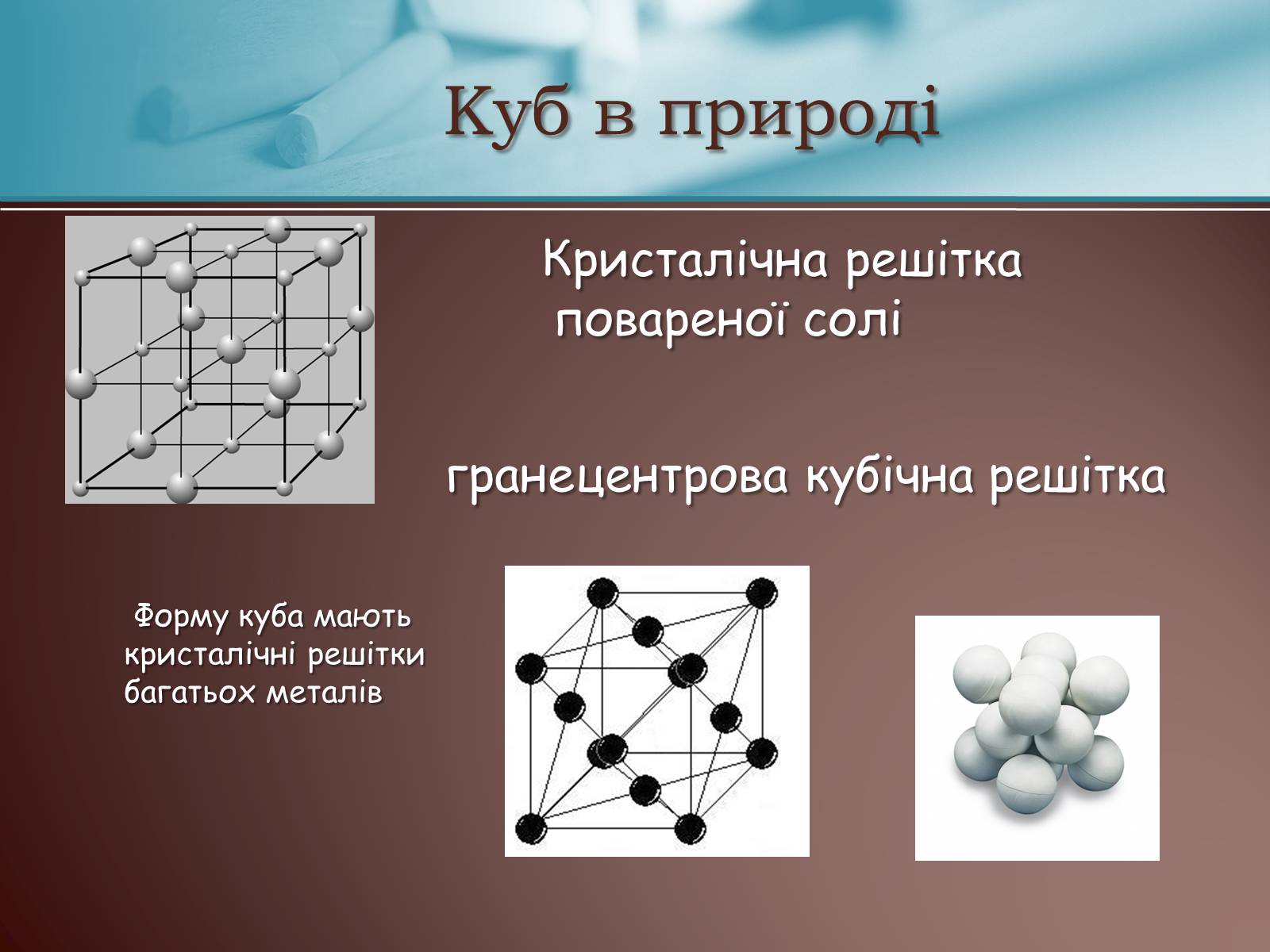
Кристалічна решітка повареної солі
гранецентрова кубічна решітка
Форму куба маютькристалічні решіткибагатьох металів
Куб в природі
гранецентрова кубічна решітка
Форму куба маютькристалічні решіткибагатьох металів
Куб в природі
Слайд #13
Правильний додекаедр
складений з дванадцяти правильних п'ятикутників;
кожна вершина додекаедра є
вершиною трьох правильних п'ятикутників.
Отже, сума плоских кутів при при кожній вершині рівна 324.
складений з дванадцяти правильних п'ятикутників;
кожна вершина додекаедра є
вершиною трьох правильних п'ятикутників.
Отже, сума плоских кутів при при кожній вершині рівна 324.
Слайд #14
Вірус поліомієліту Репродукція картини С.Далі «Тайна вечеря»
Додекаедр в природі
Додекаедр в природі
Слайд #15
Тіла Архімеда
Архімедові тіла – напівправильні опуклі многогранники, в яких всі двогранні кути рівні , а грані правильні многокутники різних типів
Архімедові тіла – напівправильні опуклі многогранники, в яких всі двогранні кути рівні , а грані правильні многокутники різних типів
Слайд #16
Тіла Пуансона
Малий зірковийдодекаедр
Великий зірковий додекаедр
Великий ікосаедр
Великий додекаедр
Малий зірковийдодекаедр
Великий зірковий додекаедр
Великий ікосаедр
Великий додекаедр
Слайд #17
Презентацію виконали: учні 11-Б класу Федчишина Юлія
