- Головна
- Готові шкільні презентації
- Презентація на тему «Применение производной к исследованию и построению графиков функций»
Презентація на тему «Применение производной к исследованию и построению графиков функций»
239
Слайд #1
Презентация по алгебре на тему: «Применение производной к исследованию и построению графиков функций»
Над проектом работали
Над проектом работали

Слайд #2
Содержание
1. Применение производной к исследованию функции
а) Теорема 1
б) Теорема 2
2. Правило нахождения интервалов монотонности
а) Пример №1
б) Пример №2
3. Экстремумы функции
а) Теорема
б) Пример №3
в) Пример №4
4. Викторина по пройденной теме :«Верно ли?»
5. Ответы
1. Применение производной к исследованию функции
а) Теорема 1
б) Теорема 2
2. Правило нахождения интервалов монотонности
а) Пример №1
б) Пример №2
3. Экстремумы функции
а) Теорема
б) Пример №3
в) Пример №4
4. Викторина по пройденной теме :«Верно ли?»
5. Ответы

Слайд #3
Применение производной к исследованию функции
1) промежутки возрастания,
убывания
3) наибольшее и наименьшее
значение функции
2) точки экстремума и значение
функции в этих точках
4) построение графика функции
1) промежутки возрастания,
убывания
3) наибольшее и наименьшее
значение функции
2) точки экстремума и значение
функции в этих точках
4) построение графика функции
Слайд #4
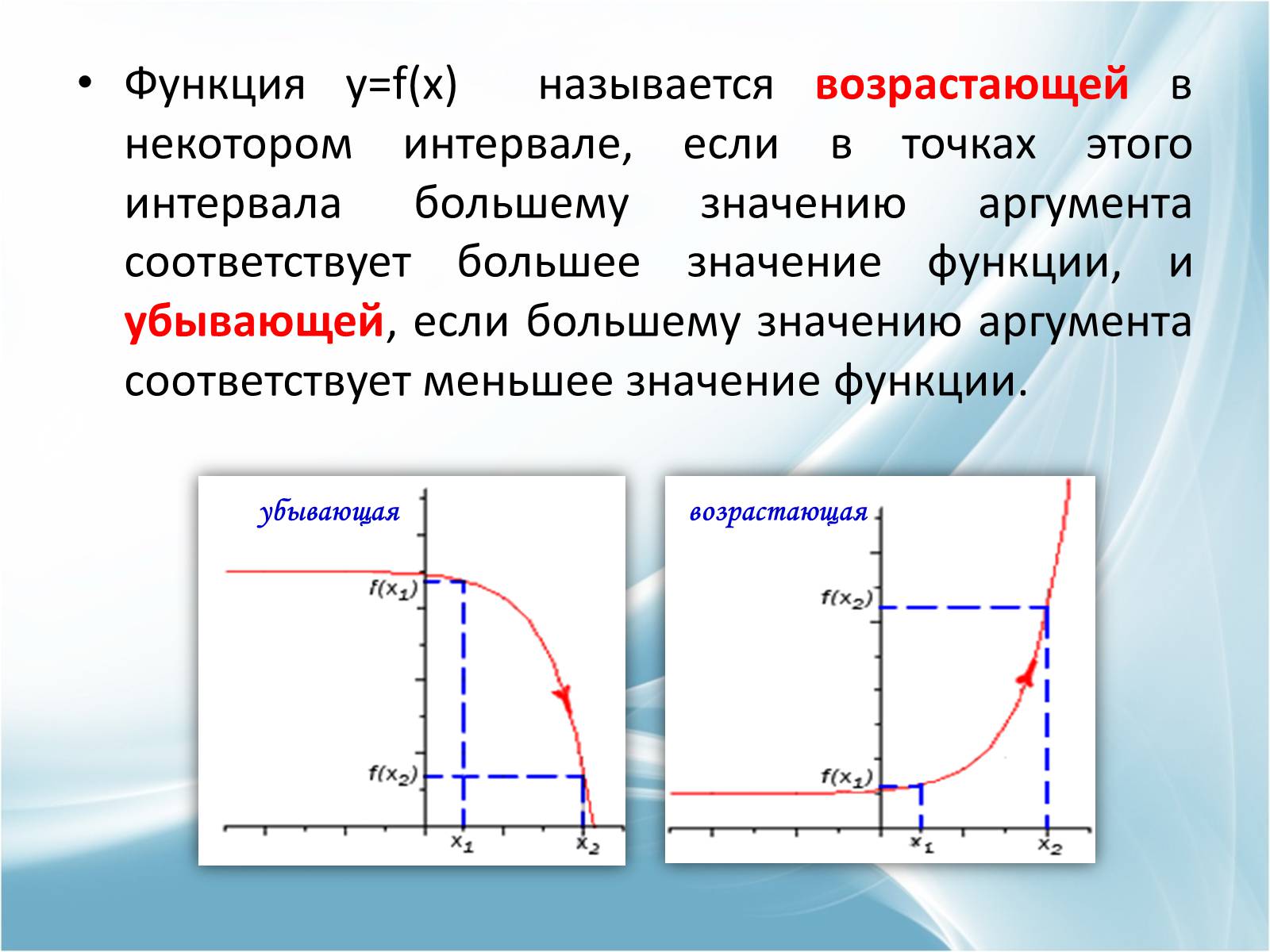
Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого интервала большему значению аргумента соответствует большее значение функции, и убывающей, если большему значению аргумента соответствует меньшее значение функции.
убывающая
возрастающая
убывающая
возрастающая
Слайд #5
Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная этой функции не отрицательна (не положительна) в этом интервале.
Теорема 1.
Теорема 1.

Слайд #6
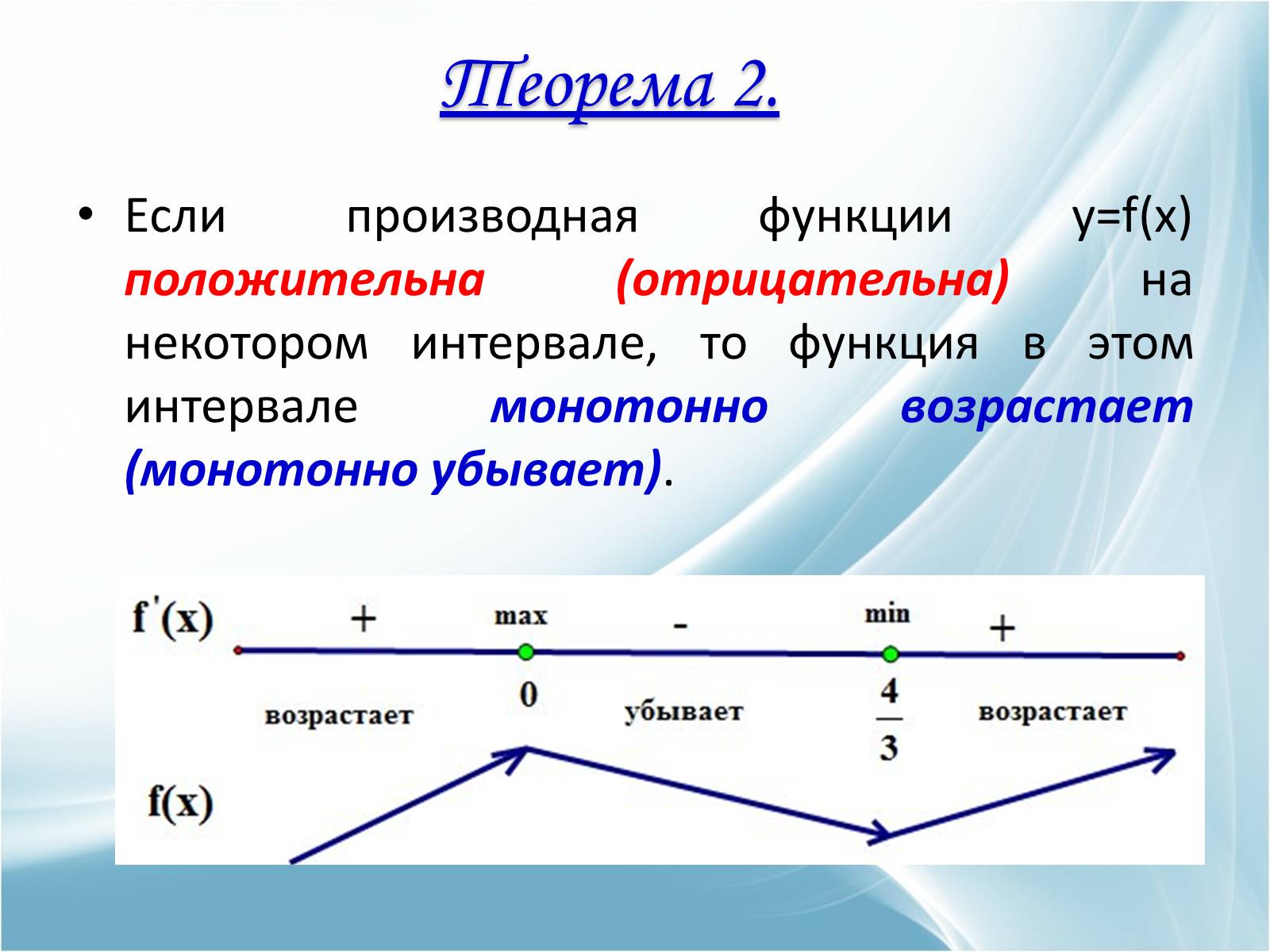
Если производная функции y=f(x) положительна (отрицательна) на некотором интервале, то функция в этом интервале монотонно возрастает (монотонно убывает).
Теорема 2.
Теорема 2.
Слайд #7
Находим область определения функции f(x).
Вычисляем производную f'(x) данной функции.
Находим точки, в которых f'(x)=0 или не существует. Эти точки называются критическими для функции f(x).
Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.
Исследуем знак f'(x) на каждом интервале. Если f'(x)›0, то на этом интервале f(x) возрастает; если f'(x)‹0, то на таком интервале функция f(x) убывает.
Правило нахождения интервалов монотонности
Вычисляем производную f'(x) данной функции.
Находим точки, в которых f'(x)=0 или не существует. Эти точки называются критическими для функции f(x).
Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.
Исследуем знак f'(x) на каждом интервале. Если f'(x)›0, то на этом интервале f(x) возрастает; если f'(x)‹0, то на таком интервале функция f(x) убывает.
Правило нахождения интервалов монотонности

Слайд #8
Область определения: R. Функция непрерывна.
Вычисляем производную : y'=6x²-6x-36.
Находим критические точки: y'=0.
x²-x-6=0
Д=1-4×(-6)×1=1+24=25
Делим область определения на интервалы:
Функция возрастает при xϵ(-∞;-2]υ[3;+∞), функция убывает при xϵ[-2;3].
Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5
+
+
-
-2
3
Вычисляем производную : y'=6x²-6x-36.
Находим критические точки: y'=0.
x²-x-6=0
Д=1-4×(-6)×1=1+24=25
Делим область определения на интервалы:
Функция возрастает при xϵ(-∞;-2]υ[3;+∞), функция убывает при xϵ[-2;3].
Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5
+
+
-
-2
3

Слайд #9
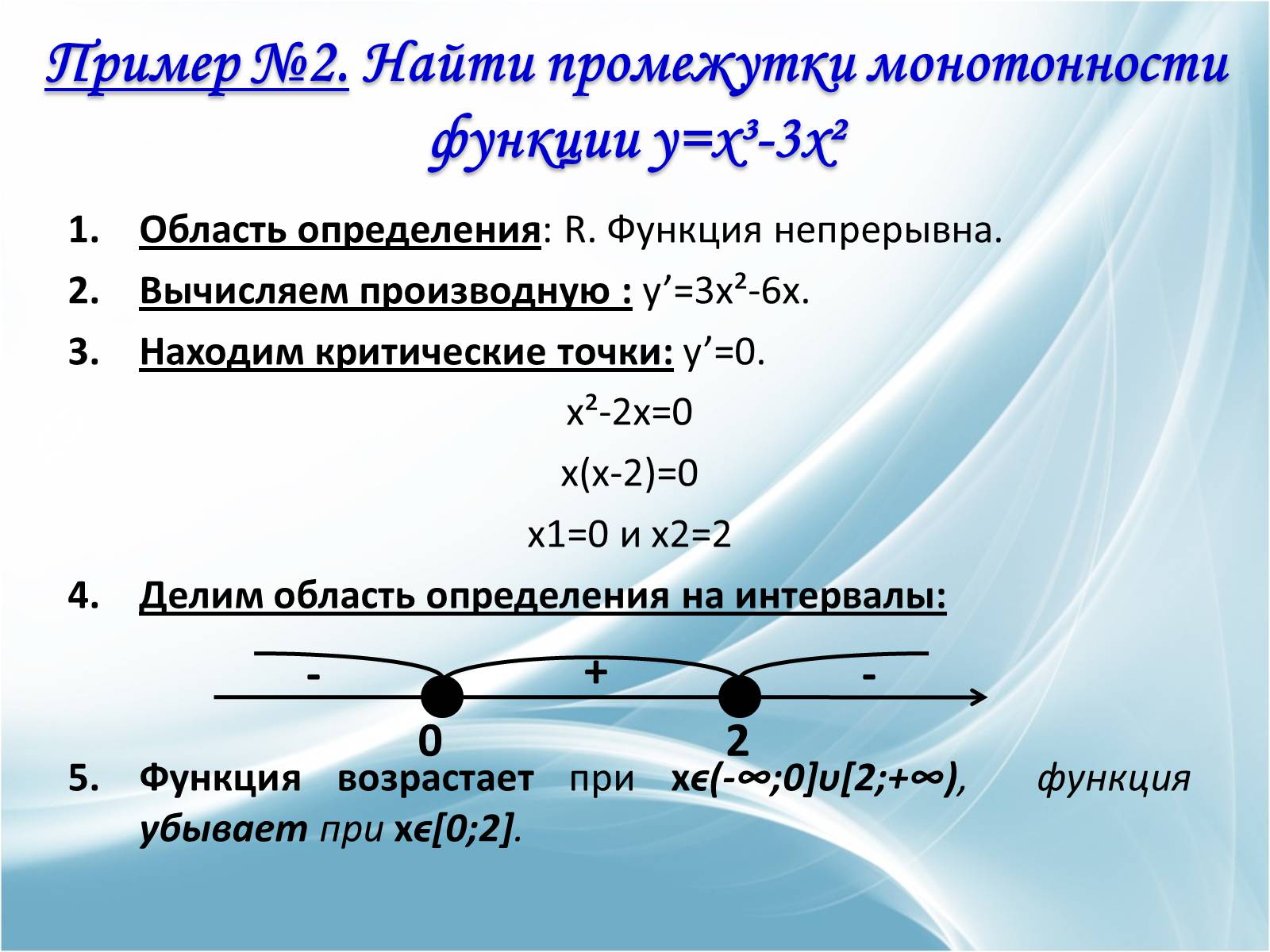
Область определения: R. Функция непрерывна.
Вычисляем производную : y'=3x²-6x.
Находим критические точки: y'=0.
x²-2x=0
x(x-2)=0
x1=0 и x2=2
Делим область определения на интервалы:
Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].
Пример №2. Найти промежутки монотонности функции y=x³-3x²
-
-
+
2
Вычисляем производную : y'=3x²-6x.
Находим критические точки: y'=0.
x²-2x=0
x(x-2)=0
x1=0 и x2=2
Делим область определения на интервалы:
Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].
Пример №2. Найти промежутки монотонности функции y=x³-3x²
-
-
+
2
Слайд #10
Экстремум функции.
Точки минимума и максимума функции называют точками экстремума.
Точками экстремума функции могут быть только её критические точки (внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции).
Точки минимума и максимума функции называют точками экстремума.
Точками экстремума функции могут быть только её критические точки (внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции).

Слайд #11
Достаточное условие существования экстремума функции:
Теорема. Если производная f'(x) при переходе через критическую точку x0 меняет знак, то точка x0 является точкой экстремума функции f(x).
Если при переходе через критическую точку х0 функции f(x) ее производная меняет знак с «+» на «-», то х0 – точка максимума функции f(x).
Если при переходе через критическую точку х0 функции f(x) ее производная меняет знак с «-» на «+», то х0 – точка минимума функции f(x).
3) Если при переходе через критическую точку х0 функции f(x) ее производная не меняет знака, то в точке х0 экстремума нет.
11
Теорема. Если производная f'(x) при переходе через критическую точку x0 меняет знак, то точка x0 является точкой экстремума функции f(x).
Если при переходе через критическую точку х0 функции f(x) ее производная меняет знак с «+» на «-», то х0 – точка максимума функции f(x).
Если при переходе через критическую точку х0 функции f(x) ее производная меняет знак с «-» на «+», то х0 – точка минимума функции f(x).
3) Если при переходе через критическую точку х0 функции f(x) ее производная не меняет знака, то в точке х0 экстремума нет.
11

Слайд #12
Область определения: R. Функция непрерывна.
Вычисляем производную : y'=-6x²-6x+12.
Находим критические точки: y'=0.
-x²-x+2=0
Д=1-4*(-1)*2=1+8=9
x1=1; x2=-2
Делим область определения на интервалы:
x=-2 – точка минимума. Найдём минимум функции ymin=-24. x=1 – точка максимума. Найдём максимум функции: ymax=3.
Пример №3. Найти экстремумы функции y=-2x³-3x²+12x-4
-
-
+
-2
1
Вычисляем производную : y'=-6x²-6x+12.
Находим критические точки: y'=0.
-x²-x+2=0
Д=1-4*(-1)*2=1+8=9
x1=1; x2=-2
Делим область определения на интервалы:
x=-2 – точка минимума. Найдём минимум функции ymin=-24. x=1 – точка максимума. Найдём максимум функции: ymax=3.
Пример №3. Найти экстремумы функции y=-2x³-3x²+12x-4
-
-
+
-2
1

Слайд #13
Пример №4. Исследовать на экстремум функцию y=x2+2.
Решение:
Находим область определения функции: D(y)=R.
Находим производную: y'=(x2+2)'=2x.
Приравниваем её к нулю: 2x=0, откуда x=0 – критическая точка.
Делим область определения на интервалы и определяем знаки производной на каждом интервале:
x=0 – точка минимума. Найдём минимум функции ymin=2.
+
-
Решение:
Находим область определения функции: D(y)=R.
Находим производную: y'=(x2+2)'=2x.
Приравниваем её к нулю: 2x=0, откуда x=0 – критическая точка.
Делим область определения на интервалы и определяем знаки производной на каждом интервале:
x=0 – точка минимума. Найдём минимум функции ymin=2.
+
-

Слайд #14
Верно ли?
1. Функция возрастает на [-7; 2) и (2; 8], значит она возрастает на [-7; 8]. Верно ли?
2. Производная функции в точке х0 равна 0, значит х0 - критическая точка. Верно ли?
3. Производная функции не существует в точке х0, значит х0 - критическая точка. Верно ли?
4. Критическая точка является точкой экстремума. Верно ли?
5. Точка экстремума является критической точкой. Верно ли?
1. Функция возрастает на [-7; 2) и (2; 8], значит она возрастает на [-7; 8]. Верно ли?
2. Производная функции в точке х0 равна 0, значит х0 - критическая точка. Верно ли?
3. Производная функции не существует в точке х0, значит х0 - критическая точка. Верно ли?
4. Критическая точка является точкой экстремума. Верно ли?
5. Точка экстремума является критической точкой. Верно ли?

Слайд #15
Ответы
Не верно
Верно
Верно
Не верно
Верно
Не верно
Верно
Верно
Не верно
Верно
