- Головна
- Готові шкільні презентації
- Презентація на тему «Прості числа»
Презентація на тему «Прості числа»
515
Слайд #1
Прості числа
Виконала:
ліцеїстка ІІІ-І курсуГринюк Ольга
Виконала:
ліцеїстка ІІІ-І курсуГринюк Ольга

Слайд #2
Натуральні числа 1,2,3,… - це числа, що використовуються для рахування предметів або для вказування порядкового номера того чи іншого предмета серед однорідних предметів. Будь-яке натуральне число можна записати за допомогою десяти арабських цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Слайд #3
Число 0 не є натуральним числом!!!

Слайд #4
Кожне натуральне число, більше одиниці поділяється принаймні на два числа: на 1 і на саме себе. Якщо ні на яке інше натуральне число воно націло не ділиться, називається простим, а якщо у нього є ще якісь цілі дільники, то складовим. Одиничка ж не вважається ні простим числом, ні складеним.

Слайд #5
Невелику «колекцію» простих чисел нам допоможе скласти старовинний спосіб, придуманий ще в 3 столітті до нашої ери Эратосфеном Киренским, зберігачем знаменитої Олександрійської бібліотеки

Слайд #6
Випишемо кілька поспіль йдуть чисел, починаючи з 2.Двойку відберемо в свою колекцію, а інші числа, кратні 2,закреслимо. Найближчим не закресленим числом буде 3.Возьмем в колекцію і його , а всі інші числа кратні 3, закреслимо. При цьому виявиться, що деякі числа вже були викреслені раніше, як, наприклад, 6, 12 та інші. Наступне найменше не закреслене число-це 5.Берем п'ятірку, а інші числа, кратні 5, закреслюємо. Повторюючи цю процедуру знову і знову, ми зрештою доможемося того, що не закресленими залишаться одні лише прості числа - вони немов просіялись крізь решето. Тому такий спосіб і отримав назву «решето Ератосфена».
«Решето Ератосфена»
«Решето Ератосфена»

Слайд #7
Чи можна, вторячи поетові, сказати, що простих чисел стільки «скільки зірок на небі, скільки риб у воді»? Відповідь знаходиться у дев'ятій книзі знаменитих творів Евкліда. Двадцята теорема в цій книзі стверджує: «Перше простих чисел існує більше будь-якого зазначеного числа їх».

Слайд #8
Припустимо ,що існує якесь найбільше просте число p. Тоді перемножимо всі прості числа, починаючи з 2 і закінчуючи p , і збільшимо отримане твірне на одиницю: 2*3*5*7*.....P+1=М. Якщо число М складене , то воно повинно мати принаймні 1 простий дільник . Але цим дільником не може бути ні одне з простих чисел 2, 3, 5, 7...P, оскільки при поділі М на кожне з них отримуємо в залишку 1. Отже, число М або саме просте, або ділиться на просте число більше P . Значить припущення, що існує найбільше просте число P , невірно і безліч простих чисел нескінченно.
Ось доказ цієї теореми!
Ось доказ цієї теореми!

Слайд #9
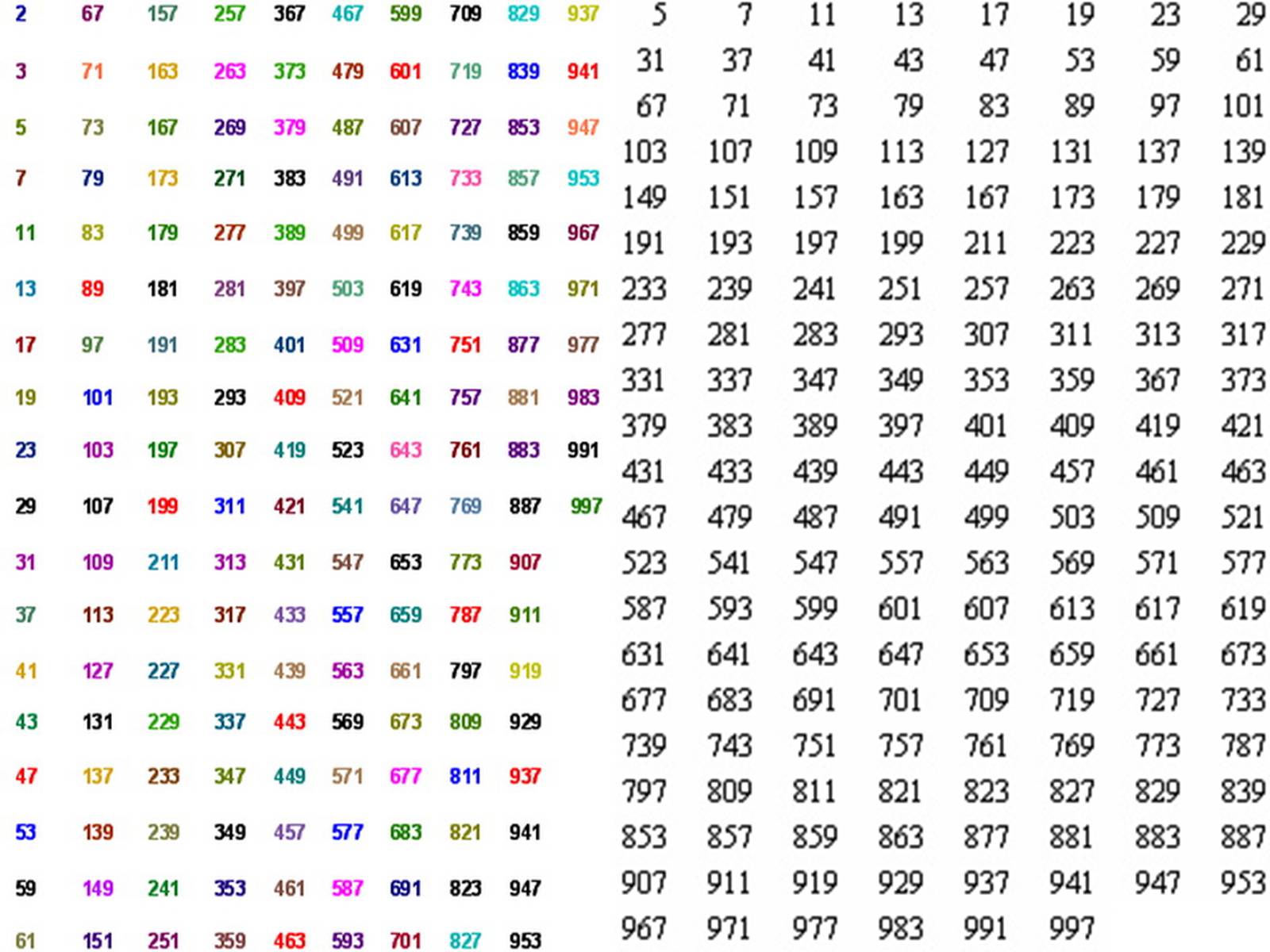
Першу відому нам таблицю простих чисел склав італійський математик П'єтро Антоніо Катальді в 1603 р. Вона охоплювала всі прості числа від 2 до 743.

Слайд #10
Першу відому нам таблицю простих чисел склав італійський математик П'єтро Антоніо Катальді в 1603 р. Вона охоплювала всі прості числа від 2 до 743.
Слайд #11
У 1770 р. німецький математик Йоганн Генріх Ламберт опублікував таблицю найменших дільників чисел , не переважаючих 102000 і не діляться на 2, 3, 5. Вклавши в цю працю воістину колосальні зусилля, Ламберт гарантував безсмертя тому, хто доведе таблицю дільників до мільйона. На його заклик відгукнулися багато обчислювачів.

Слайд #12
У мисливців за числами найбільше популярний Мерсенна. Вони названі на честь французького вченого Марена Марсенна, що зіграв у XVIII ст. Значну роль становлення європейської науки.

Слайд #13
Деякі поданні про розподіл простих чисел мали вже стародавні греки. З доведення Евкліда випливає, наприклад, що вони не зібрані разом, а розкидані по всій числовій осі. Але як часто?

Слайд #14
У 1845 р. французький математик Жозедо Бертран, досліджуючи таблицю простих чисел у проміжку від 1 до 6000000 виявив, що між числами n історія 2n - 2где n >3, міститься принаймні одне просте число. Згодом ця властивість одержала назву постулата Бертрана, хоча самому Бертрану обґрунтувати його так і не вдалось.

Слайд #15
Дії над натуральними числами

Слайд #16
а + b = b + а (а + b) + с = а + (b + с)а + 0 = 0 + а = а
Додавання
Додавання

Слайд #17
а + b = b + а (а + b) + с = а + (b + с)а + 0 = 0 + а = а
Додавання
Додавання

Слайд #18
Віднімання – операція, обернена до додавання.(а + b) – с = (а - с) + bа – (b + с) = (а - b) – са + (b – с) = (а + b) – са – (b - с) = а – b + с
Віднімання
Віднімання

Слайд #19
Віднімання – операція, обернена до додавання.(а + b) – с = (а - с) + bа – (b + с) = (а - b) – са + (b – с) = (а + b) – са – (b - с) = а – b + с
Віднімання
Віднімання

Слайд #20
Множення
а ∙ b = b ∙ а а ∙ b ∙ с = а ∙ (b ∙ с)(а + b) ∙ с= а ∙ с + b ∙ с(а – b) ∙ с = а ∙ с – b ∙ са ∙ 1 = 1 ∙ а = аа ∙ 0 = 0 ∙ а = 00 ∙ 0 = 01 ∙ 1 = 1
а ∙ b = b ∙ а а ∙ b ∙ с = а ∙ (b ∙ с)(а + b) ∙ с= а ∙ с + b ∙ с(а – b) ∙ с = а ∙ с – b ∙ са ∙ 1 = 1 ∙ а = аа ∙ 0 = 0 ∙ а = 00 ∙ 0 = 01 ∙ 1 = 1
Слайд #21
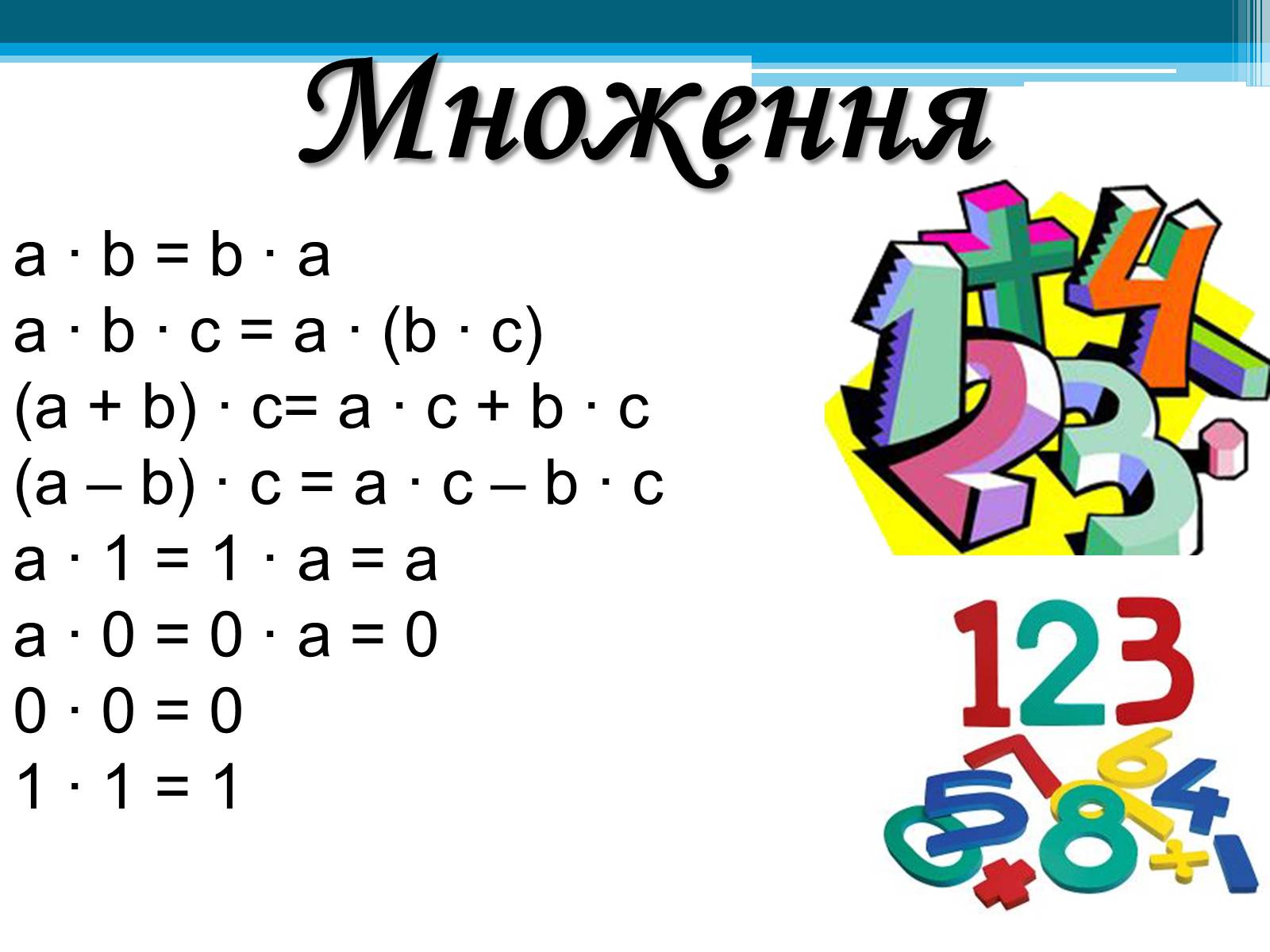
Множення
а ∙ b = b ∙ а а ∙ b ∙ с = а ∙ (b ∙ с)(а + b) ∙ с= а ∙ с + b ∙ с(а – b) ∙ с = а ∙ с – b ∙ са ∙ 1 = 1 ∙ а = аа ∙ 0 = 0 ∙ а = 00 ∙ 0 = 01 ∙ 1 = 1
а ∙ b = b ∙ а а ∙ b ∙ с = а ∙ (b ∙ с)(а + b) ∙ с= а ∙ с + b ∙ с(а – b) ∙ с = а ∙ с – b ∙ са ∙ 1 = 1 ∙ а = аа ∙ 0 = 0 ∙ а = 00 ∙ 0 = 01 ∙ 1 = 1

Слайд #22
Ділення – операція, обернена до множення.Якщо b ∙ с = а, тоа : 1 = aa : a = 1, a ≠ 00 : a = 0, a ≠ 0
(а ∙ b) : c = (a :c) ∙ b(а ∙ b) : c = (b :c) ∙ a(a ∙ b) : c = a : (b ∙ c)
Ділення
(а ∙ b) : c = (a :c) ∙ b(а ∙ b) : c = (b :c) ∙ a(a ∙ b) : c = a : (b ∙ c)
Ділення

Слайд #23
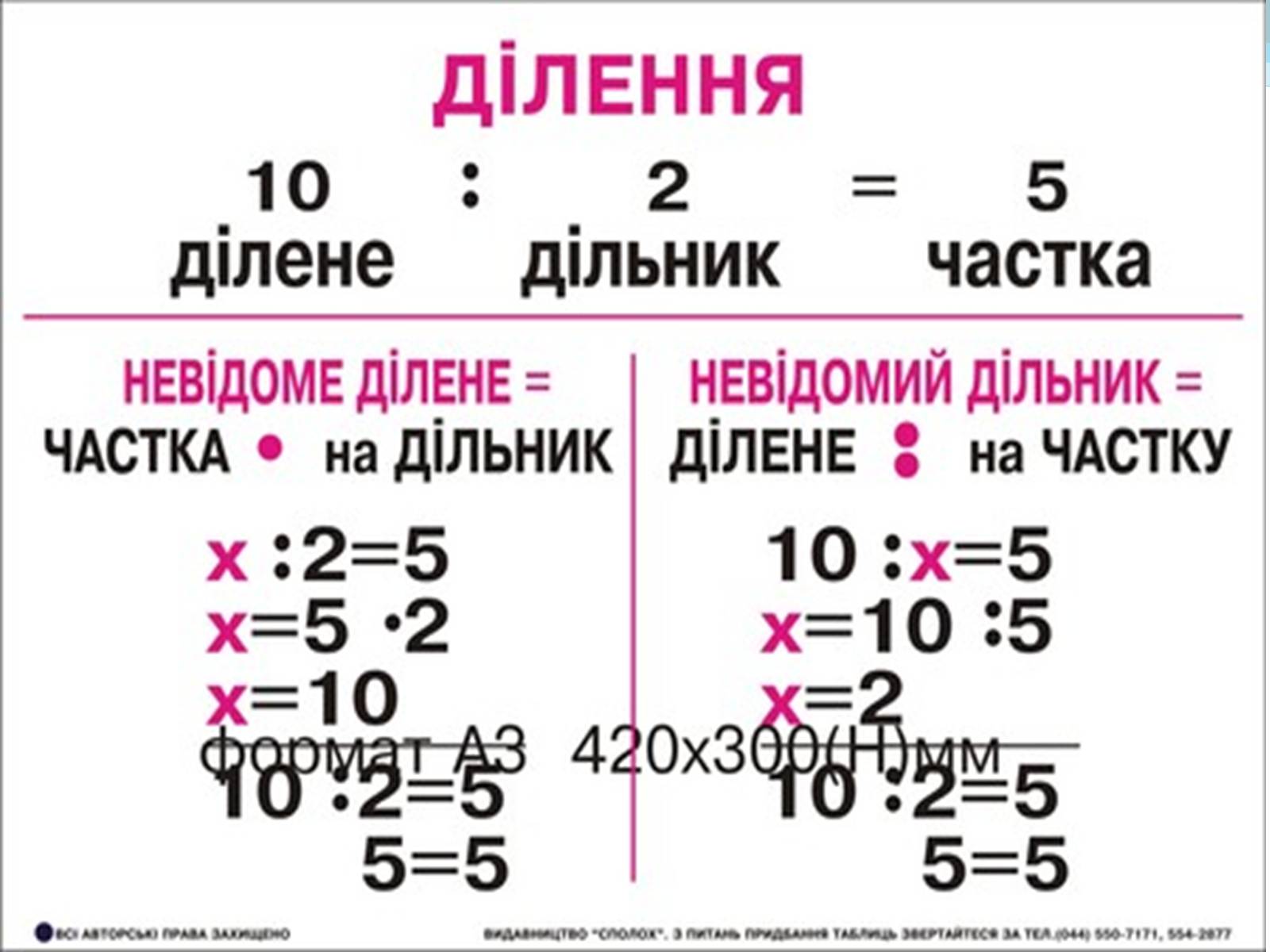
Ділення – операція, обернена до множення.Якщо b ∙ с = а, тоа : 1 = aa : a = 1, a ≠ 00 : a = 0, a ≠ 0
(а ∙ b) : c = (a :c) ∙ b(а ∙ b) : c = (b :c) ∙ a(a ∙ b) : c = a : (b ∙ c)
Ділення
(а ∙ b) : c = (a :c) ∙ b(а ∙ b) : c = (b :c) ∙ a(a ∙ b) : c = a : (b ∙ c)
Ділення
Слайд #24
Дякую
за увагу!!!
за увагу!!!
