Презентація на тему «Правильна піраміда»
373
Слайд #1
Правильна піраміда
Слайд #2
ПІРАМІДОЮ називається многогранник, одна грань якого – довільний многокутник, а інші грані – трикутники, що мають спільну вершину
Слайд #3
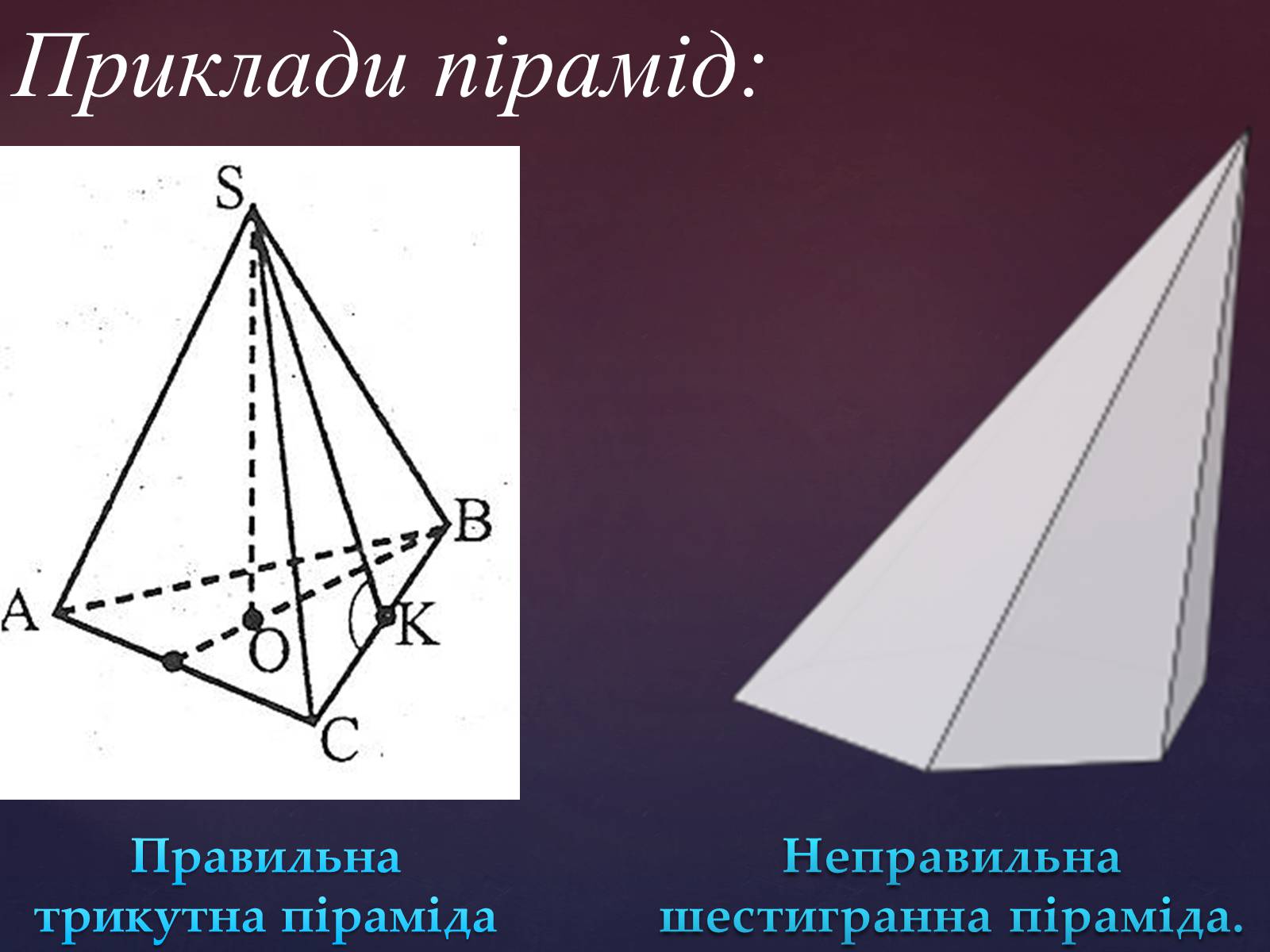
Приклади пірамід:
Правильна трикутна піраміда
Неправильна шестигранна піраміда.
Правильна трикутна піраміда
Неправильна шестигранна піраміда.
Слайд #4
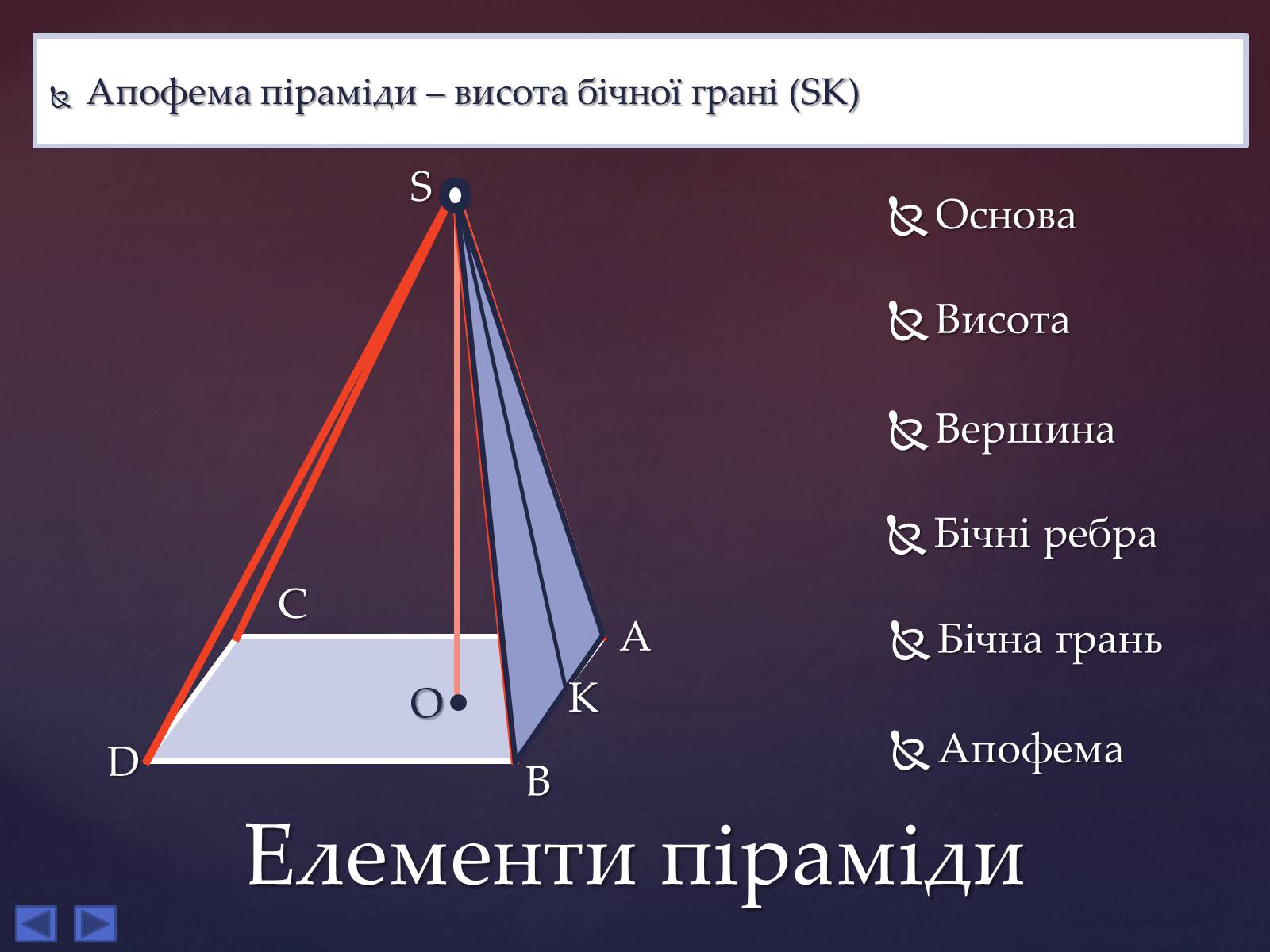
Елементи піраміди
Основа піраміди – довільний многокутник, над площиною якого розміщено вершину піраміди (ABCD)
Висота піраміди – перпендикуляр, опущений з вершини піраміди на основу (SO)
Вершина піраміди – точка, розташована на висоті піраміди, яка проектується на основу цієї піраміди (S)
Бічні ребра – Відрізки, що сполучають вершину піраміди з вершинами основи (SA, SB, SC, SD)
Бічні грані – трикутники, що мають спільну вершину та утворюють бічну поверхню піраміди (ASB, BSC, CSD, DSA)
Апофема піраміди – висота бічної грані (SK)
Основа
Висота
Вершина
Бічні ребра
Бічна грань
Апофема
S
O
A
B
C
D
K
Основа піраміди – довільний многокутник, над площиною якого розміщено вершину піраміди (ABCD)
Висота піраміди – перпендикуляр, опущений з вершини піраміди на основу (SO)
Вершина піраміди – точка, розташована на висоті піраміди, яка проектується на основу цієї піраміди (S)
Бічні ребра – Відрізки, що сполучають вершину піраміди з вершинами основи (SA, SB, SC, SD)
Бічні грані – трикутники, що мають спільну вершину та утворюють бічну поверхню піраміди (ASB, BSC, CSD, DSA)
Апофема піраміди – висота бічної грані (SK)
Основа
Висота
Вершина
Бічні ребра
Бічна грань
Апофема
S
O
A
B
C
D
K
Слайд #5
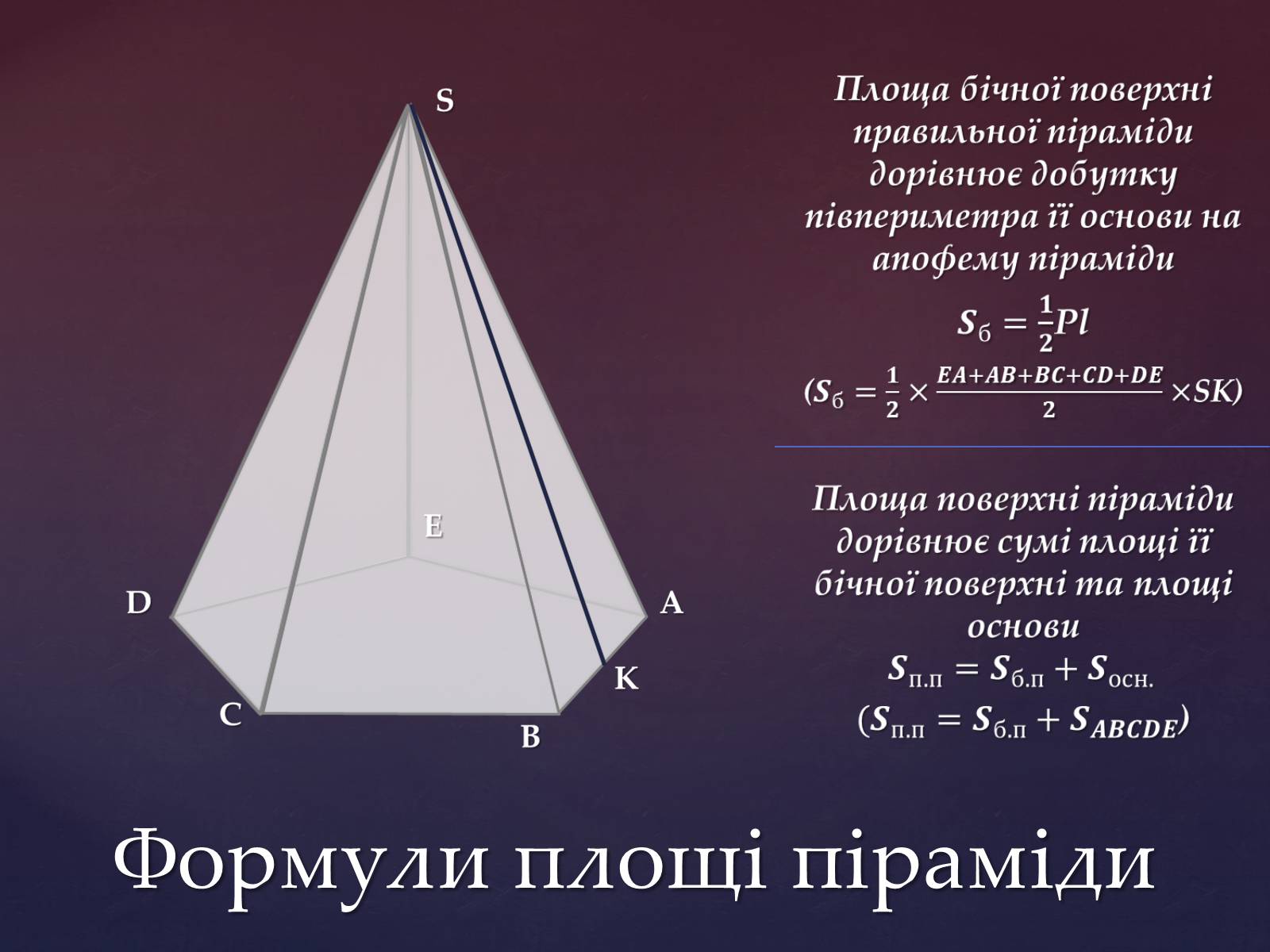
Формули площі піраміди
Слайд #6
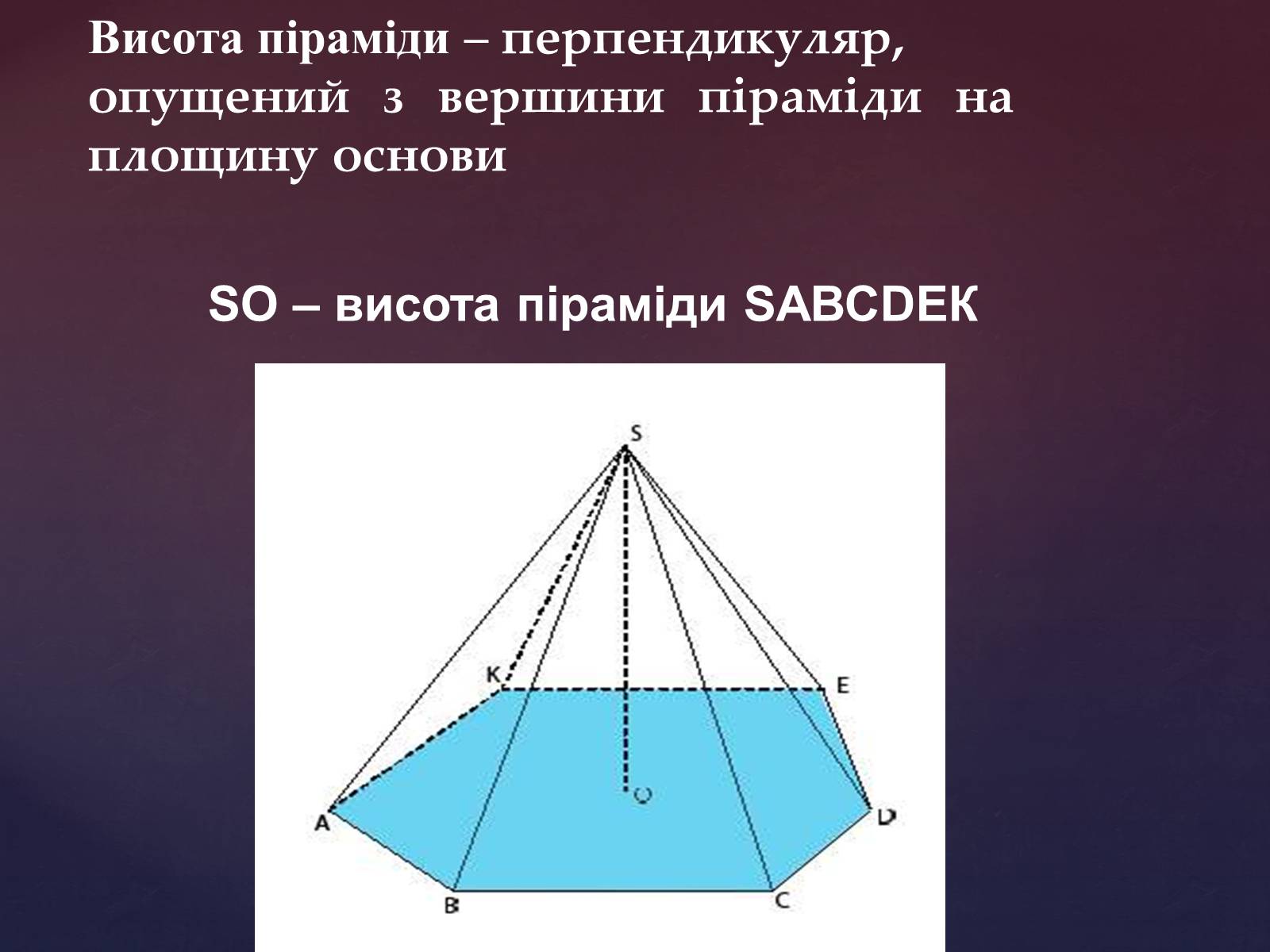
Висота піраміди – перпендикуляр,
опущений з вершини піраміди на площину основи
SO – висота піраміди SАВСDЕК
опущений з вершини піраміди на площину основи
SO – висота піраміди SАВСDЕК
Слайд #7
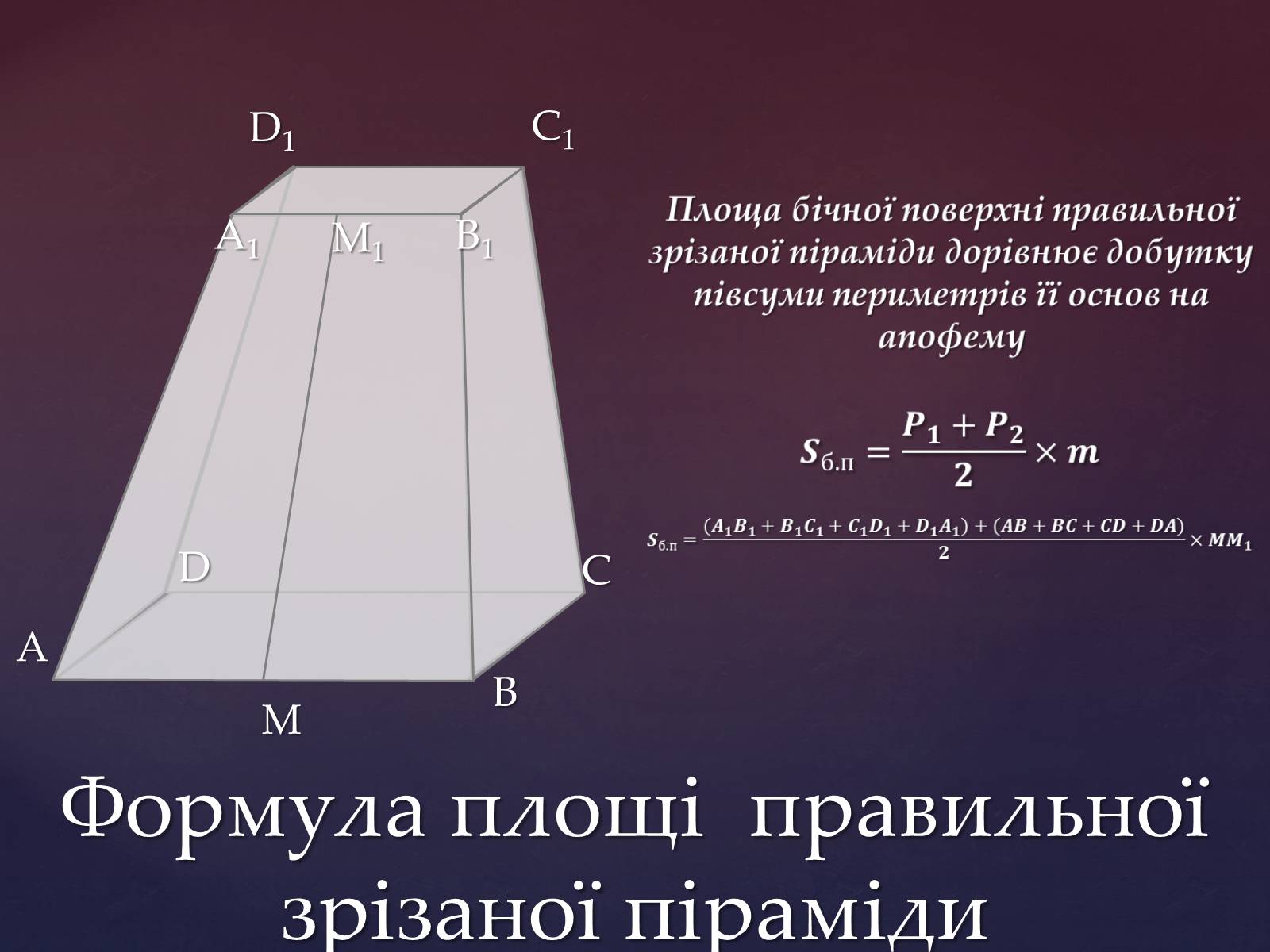
Формула площі правильної зрізаної піраміди
С1
D1
С
D
A
B
B1
A1
M1
M
Слайд #8
Тетраедр
Слайд #9
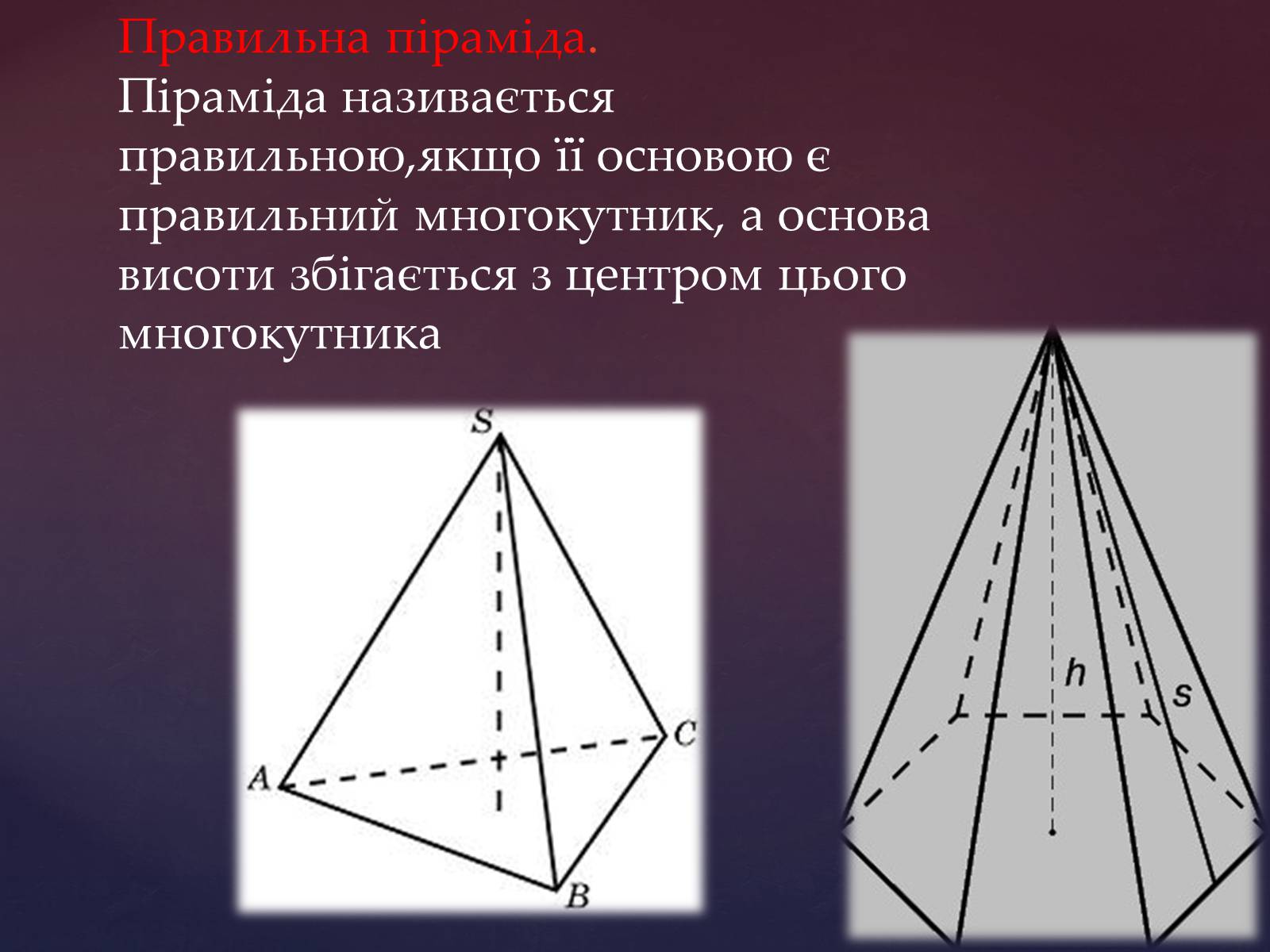
Правильна піраміда.Піраміда називається правильною,якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника
Слайд #10
Віссю правильної піраміди називається пряма, яка містить її висоту. У правильній піраміді всі бічні ребра рівні, бічні грані – рівнобедрені трикутники. Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Бічною поверхнею піраміди називається сума площ її бічних граней. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.
Слайд #11
Віссю правильної піраміди називається пряма, яка містить її висоту. У правильній піраміді всі бічні ребра рівні, бічні грані – рівнобедрені трикутники. Висота бічної грані правильної піраміди, проведена з її вершини, називається апофемою. Бічною поверхнею піраміди називається сума площ її бічних граней. Бічна поверхня правильної піраміди дорівнює добутку півпериметра основи на апофему.
Слайд #12
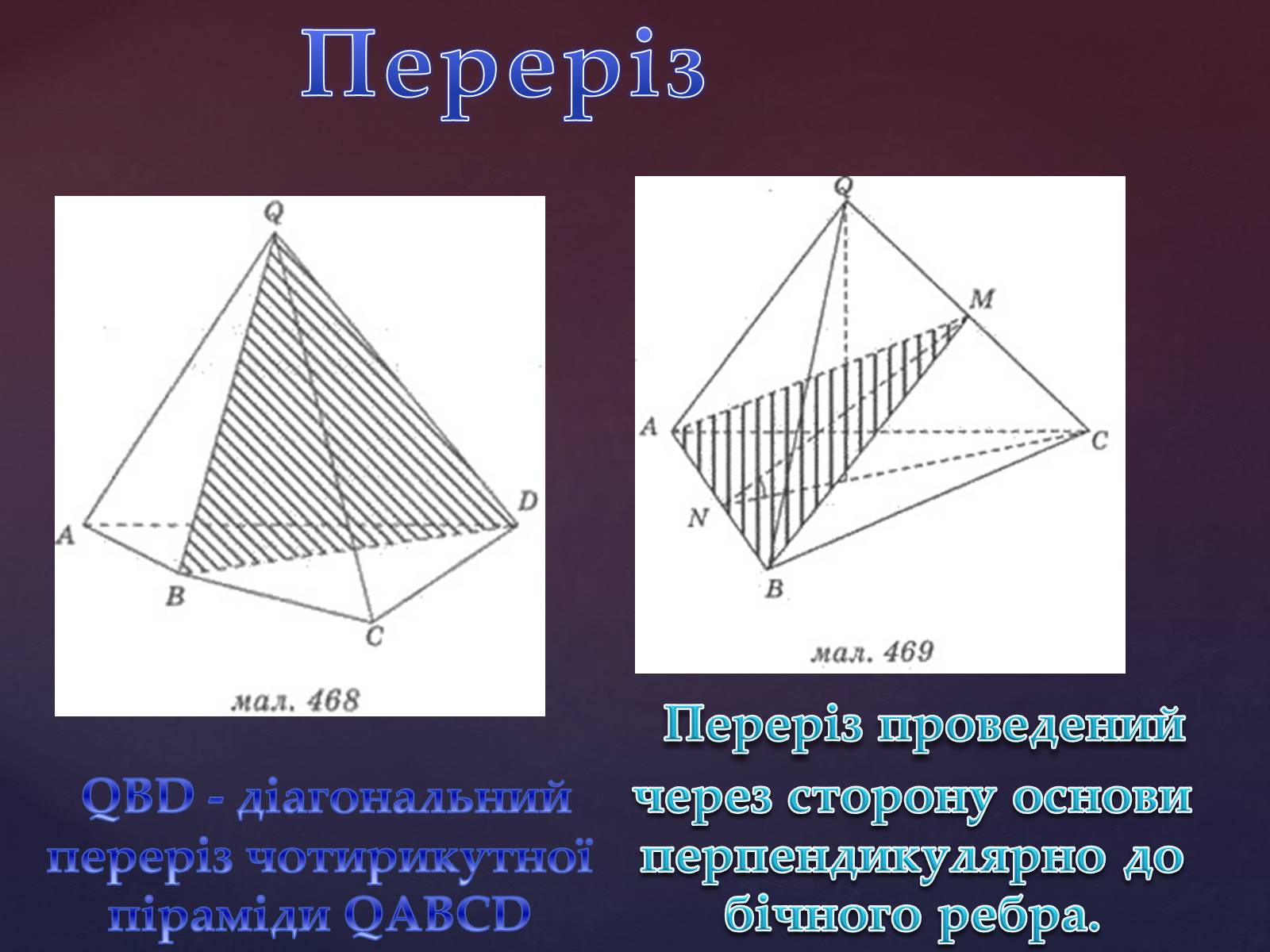
Переріз
QВD - діагональний переріз чотирикутної піраміди QАВСD
Переріз проведений через сторону основи перпендикулярно до бічного ребра.
QВD - діагональний переріз чотирикутної піраміди QАВСD
Переріз проведений через сторону основи перпендикулярно до бічного ребра.
Слайд #13
Задачі
Слайд #14
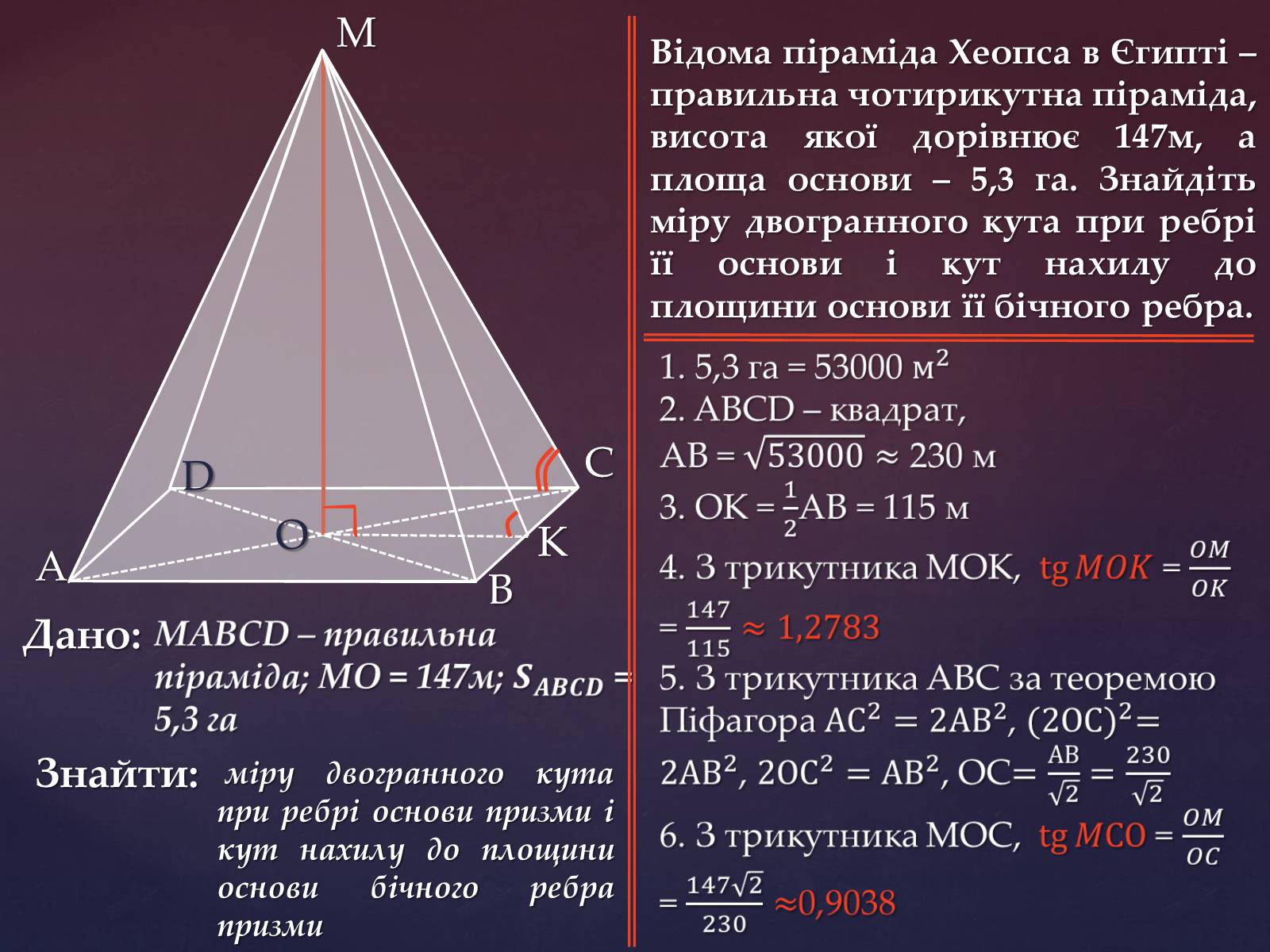
Відома піраміда Хеопса в Єгипті – правильна чотирикутна піраміда, висота якої дорівнює 147м, а площа основи – 5,3 га. Знайдіть міру двогранного кута при ребрі її основи і кут нахилу до площини основи її бічного ребра.
M
C
A
В
D
O
Дано:
Знайти:
міру двогранного кута при ребрі основи призми і кут нахилу до площини основи бічного ребра призми
K
M
C
A
В
D
O
Дано:
Знайти:
міру двогранного кута при ребрі основи призми і кут нахилу до площини основи бічного ребра призми
K
Слайд #15
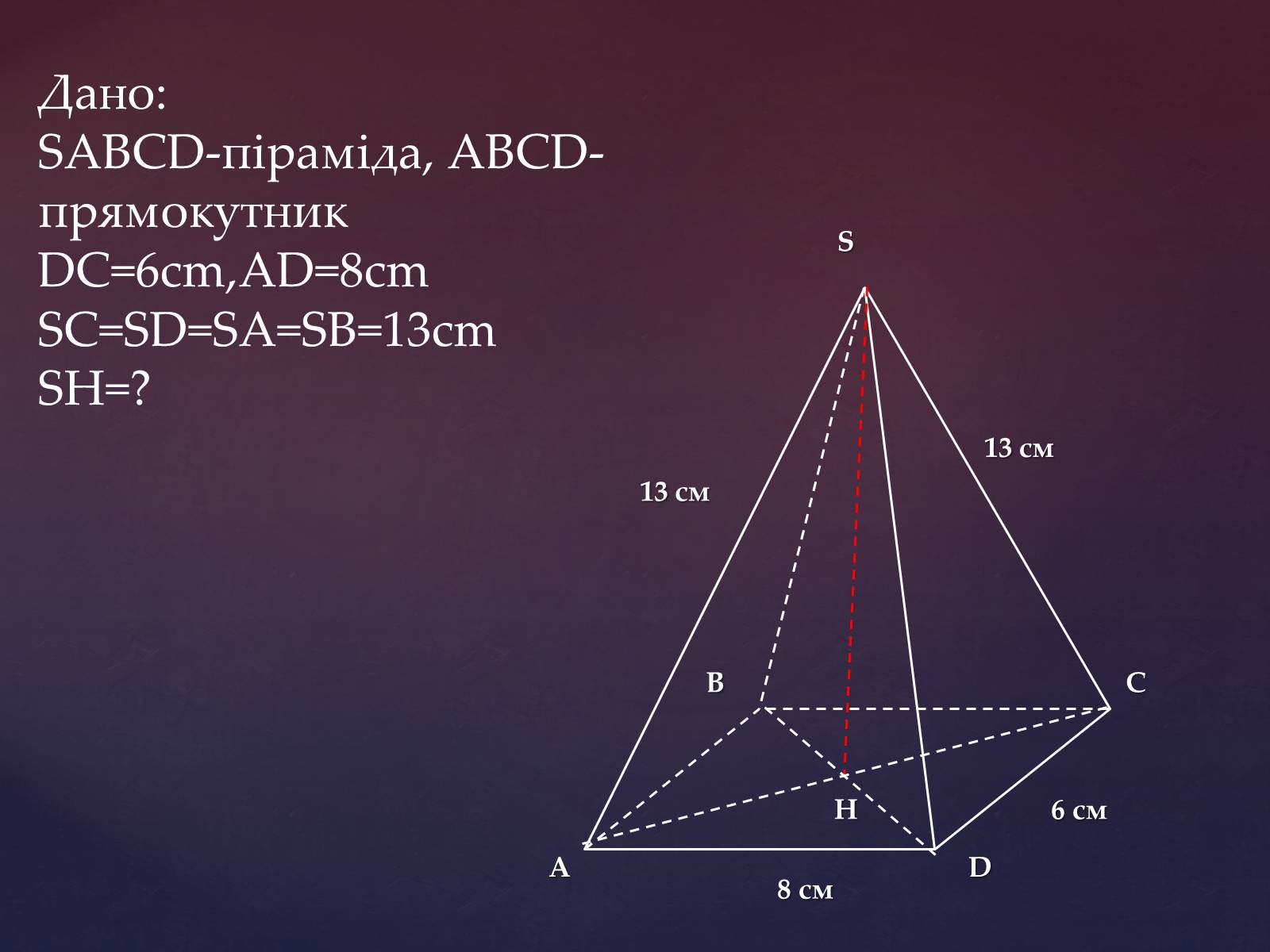
Дано:SABCD-піраміда, ABCD-прямокутник
DC=6cm,AD=8cmSC=SD=SA=SB=13cmSH=?
B
A
C
D
S
8 см
6 см
13 см
Н
13 см
DC=6cm,AD=8cmSC=SD=SA=SB=13cmSH=?
B
A
C
D
S
8 см
6 см
13 см
Н
13 см
Слайд #16
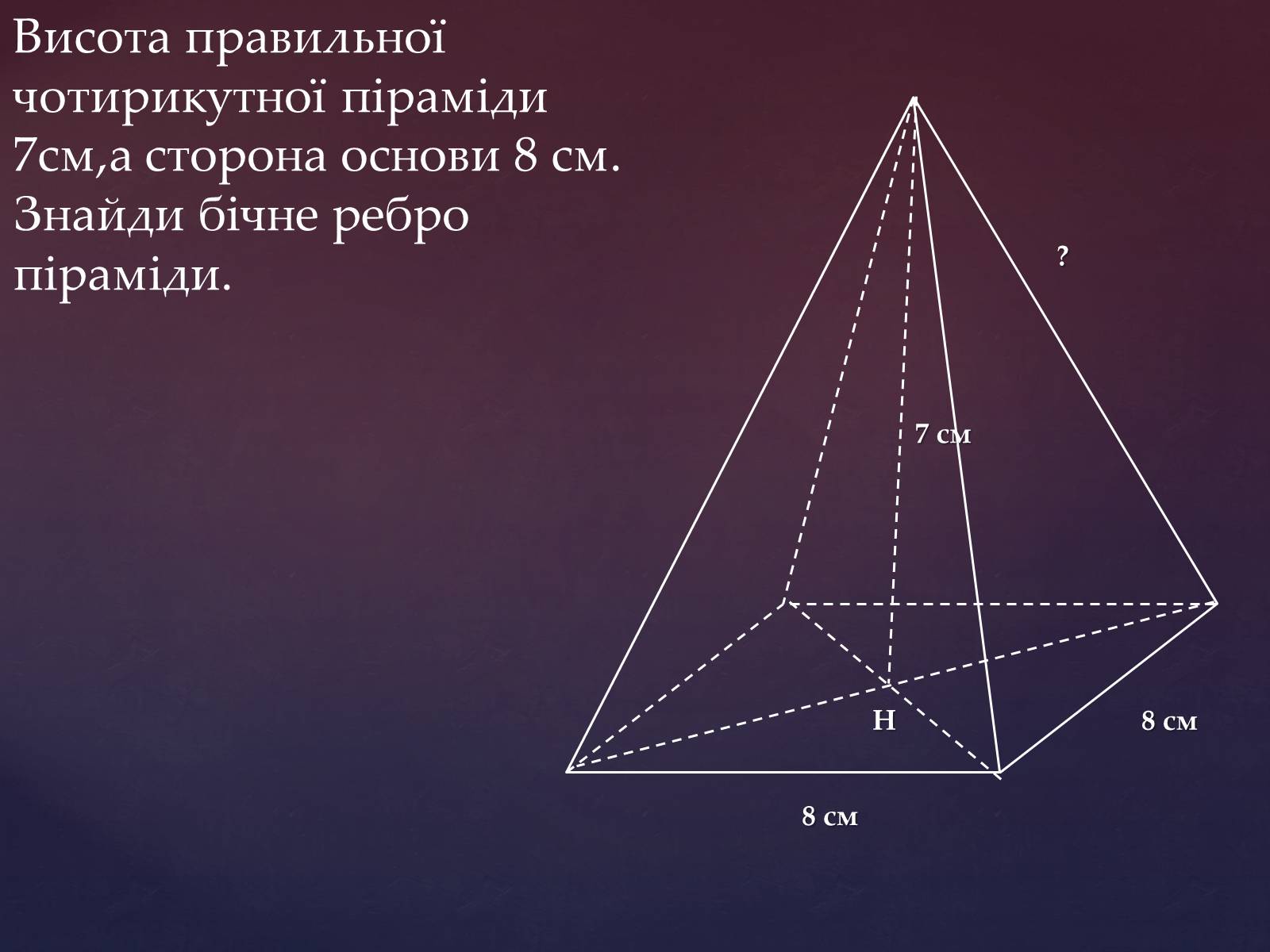
Висота правильної чотирикутної піраміди 7см,а сторона основи 8 см. Знайди бічне ребро піраміди.
8 см
8 см
Н
7 см
?
8 см
8 см
Н
7 см
?
Слайд #17
B
A
C
D
F
9 см
5 см
3 см
Н
Е
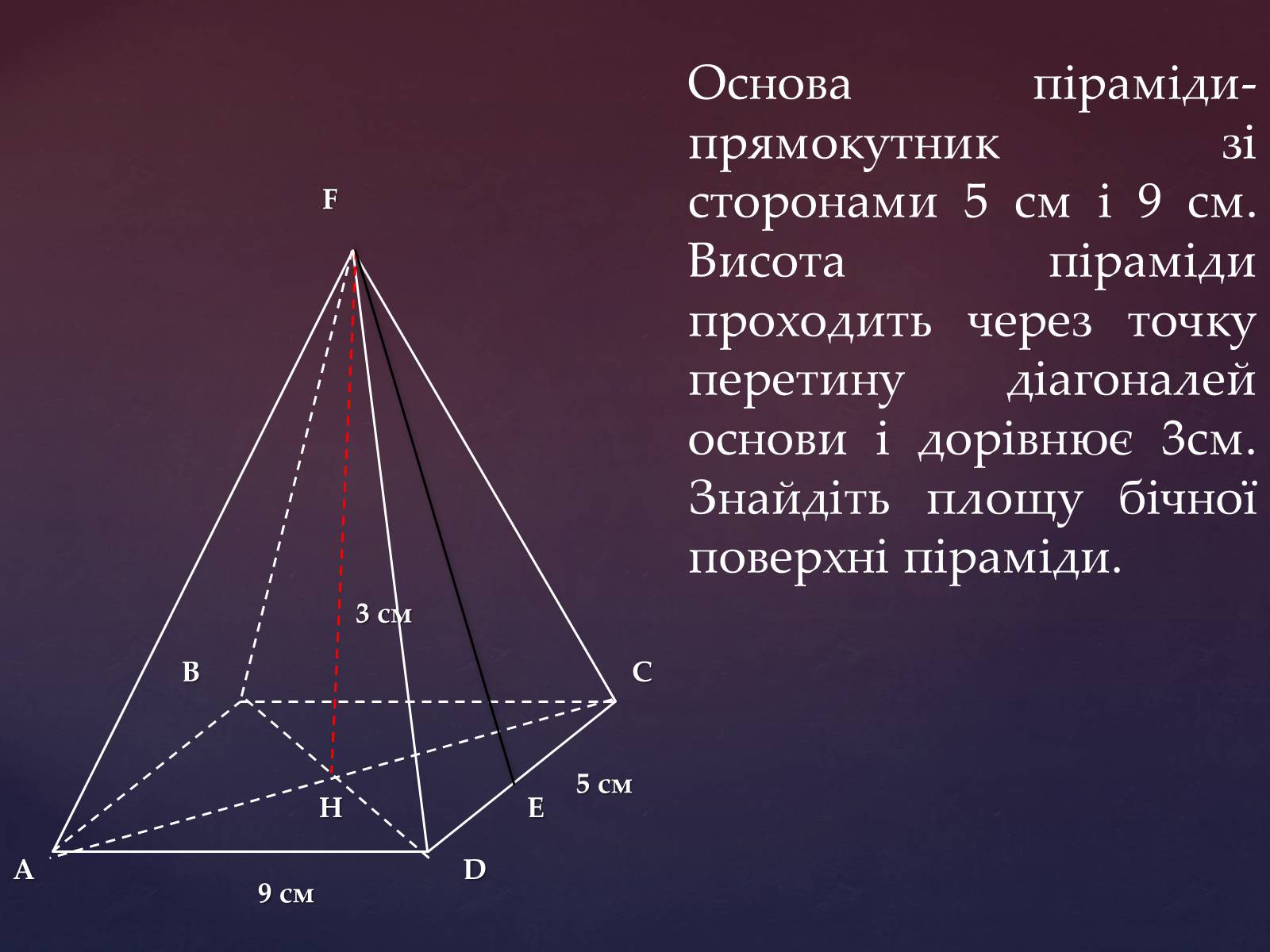
Основа піраміди-прямокутник зі сторонами 5 см і 9 см. Висота піраміди проходить через точку перетину діагоналей основи і дорівнює 3см. Знайдіть площу бічної поверхні піраміди.
A
C
D
F
9 см
5 см
3 см
Н
Е
Основа піраміди-прямокутник зі сторонами 5 см і 9 см. Висота піраміди проходить через точку перетину діагоналей основи і дорівнює 3см. Знайдіть площу бічної поверхні піраміди.
Слайд #18
Підготували
учні 11 класу СЗШ №9 м.УманіКривих Анастасія, Сидоренко Тетяна та Білоус Віктор
учні 11 класу СЗШ №9 м.УманіКривих Анастасія, Сидоренко Тетяна та Білоус Віктор
