- Головна
- Готові шкільні презентації
- Презентація на тему «Нові види чотирикутників та їх властивості»
Презентація на тему «Нові види чотирикутників та їх властивості»
230
Слайд #1
Міністерство освіти і науки, молоді та спорту України
Департамент освіти і науки Київської обласної державної адміністрації
Київський обласний комунальний позашкільний навчальний заклад
«Мала академія наук»
Відділення: математики
Секція: математики
НОВІ ВИДИ ЧОТИРИКУТНИКІВ ТА ЇХ ВЛАСТИВОСТІ
Автор:
Мітічкін Дмитро Сергійович, учень 32 групи
Науковий керівник:
Пихтар Микола Петрович, кандидат педагогічних наук, доцент кафедри комп'ютерних наук Славутицької філії НТУУ «КПІ», учитель математики вищої категорії Славутицького ліцею, Заслужений учитель України
Рецензент:
Шишкіна Ірина Олександрівна,учитель математики вищої категорії Славутицького ліцею Славутицької міської ради Київської області, «Учитель-методист»
Департамент освіти і науки Київської обласної державної адміністрації
Київський обласний комунальний позашкільний навчальний заклад
«Мала академія наук»
Відділення: математики
Секція: математики
НОВІ ВИДИ ЧОТИРИКУТНИКІВ ТА ЇХ ВЛАСТИВОСТІ
Автор:
Мітічкін Дмитро Сергійович, учень 32 групи
Науковий керівник:
Пихтар Микола Петрович, кандидат педагогічних наук, доцент кафедри комп'ютерних наук Славутицької філії НТУУ «КПІ», учитель математики вищої категорії Славутицького ліцею, Заслужений учитель України
Рецензент:
Шишкіна Ірина Олександрівна,учитель математики вищої категорії Славутицького ліцею Славутицької міської ради Київської області, «Учитель-методист»

Слайд #2
Мета роботи полягає у побудові нових видів чотирикутників, зокрема, еліптичного, параболічного, гіперболічного та у дослідженні їх основних властивостей.
Об'єктом дослідення є многокутники на площині євклідової геометрії.
Предметом дослідження є нетрадиційні види многокутників, а саме параболічний, еліптичний, гіперболічний.
Завдання науково-дослідницької роботи:
- опрацювати теоретичний матеріал, що стосується вказаної теми та виходить за межі шкільної програми;
- закріпити знання з теорії кривих ІІ порядку у процесі дослідження питання про існування нетрадиційних видів многокутників, зокрема, чотирикутників;
- визначити поняття еліптичного, параболічного, гіперболічного чотирикутників і вказати їх основні елементи та правила їх побудови;
- сформулювати і вивести основні властивості вищезгаданих фігур.
Об'єктом дослідення є многокутники на площині євклідової геометрії.
Предметом дослідження є нетрадиційні види многокутників, а саме параболічний, еліптичний, гіперболічний.
Завдання науково-дослідницької роботи:
- опрацювати теоретичний матеріал, що стосується вказаної теми та виходить за межі шкільної програми;
- закріпити знання з теорії кривих ІІ порядку у процесі дослідження питання про існування нетрадиційних видів многокутників, зокрема, чотирикутників;
- визначити поняття еліптичного, параболічного, гіперболічного чотирикутників і вказати їх основні елементи та правила їх побудови;
- сформулювати і вивести основні властивості вищезгаданих фігур.

Слайд #3
Розділ 1.
КРИВІ ІІ ПОРЯДКУ, ВИКОРИСТАННЯ ДУГ КРИВИХ ДО ПОБУДОВИ МНОГОКУТНИКІВ
.
1.1 Поняття та основні властивості кривих ІІ порядку;
1.2 Означення та правило побудови параболічного многокутника;
1.3 Означення та правило побудови еліптичного многокутника;
1.4 Означення та правило побудови параболічного многокутника;
1.5 Узагальнення многокутника з кривих ІІ порядку.
КРИВІ ІІ ПОРЯДКУ, ВИКОРИСТАННЯ ДУГ КРИВИХ ДО ПОБУДОВИ МНОГОКУТНИКІВ
.
1.1 Поняття та основні властивості кривих ІІ порядку;
1.2 Означення та правило побудови параболічного многокутника;
1.3 Означення та правило побудови еліптичного многокутника;
1.4 Означення та правило побудови параболічного многокутника;
1.5 Узагальнення многокутника з кривих ІІ порядку.

Слайд #4
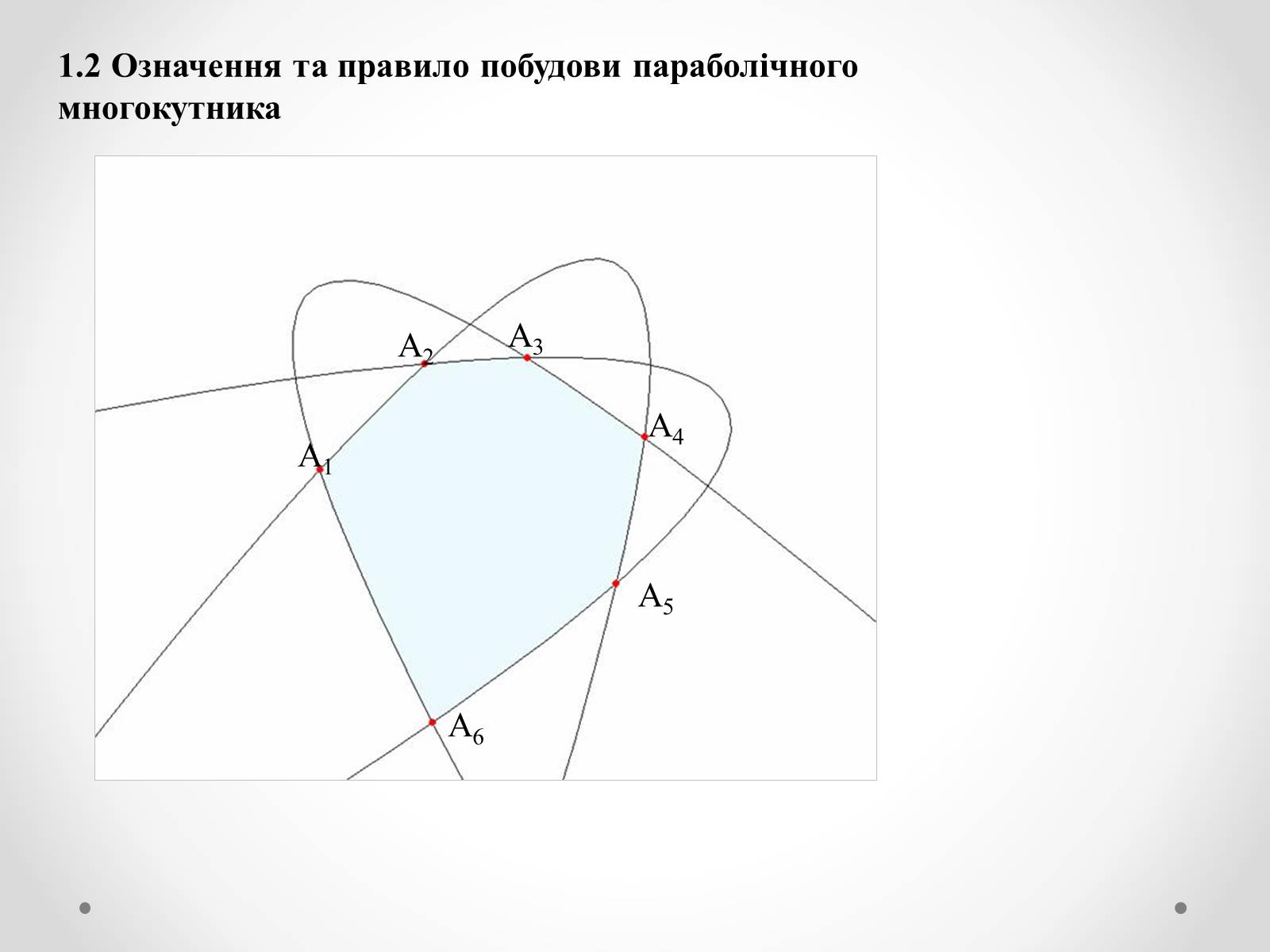
1.2 Означення та правило побудови параболічного многокутника
A1
A2
A3
A4
A5
A6
A1
A2
A3
A4
A5
A6
Слайд #5
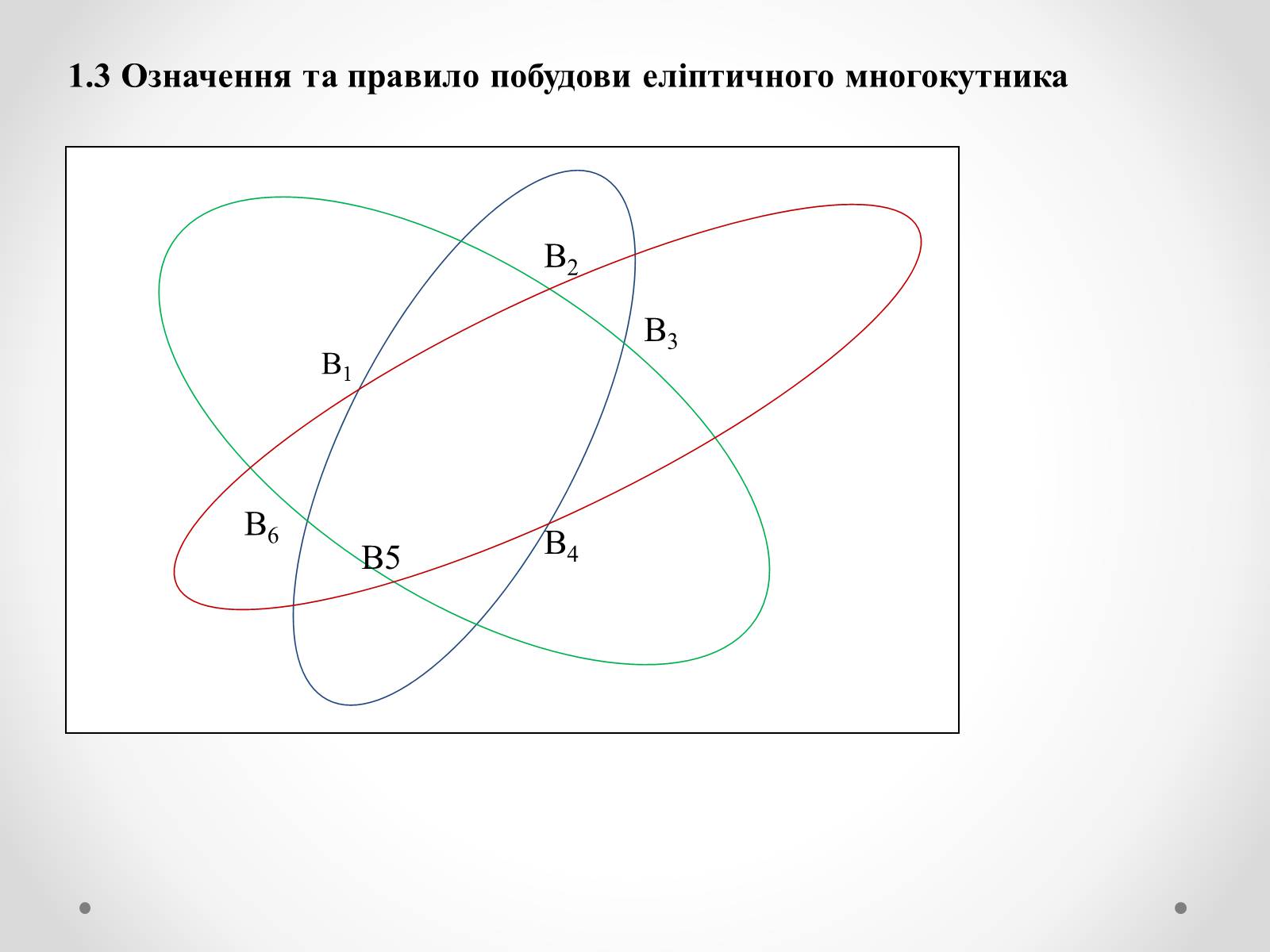
1.3 Означення та правило побудови еліптичного многокутника
B1
B4
B3
B6
B5
B2
B1
B4
B3
B6
B5
B2
Слайд #6
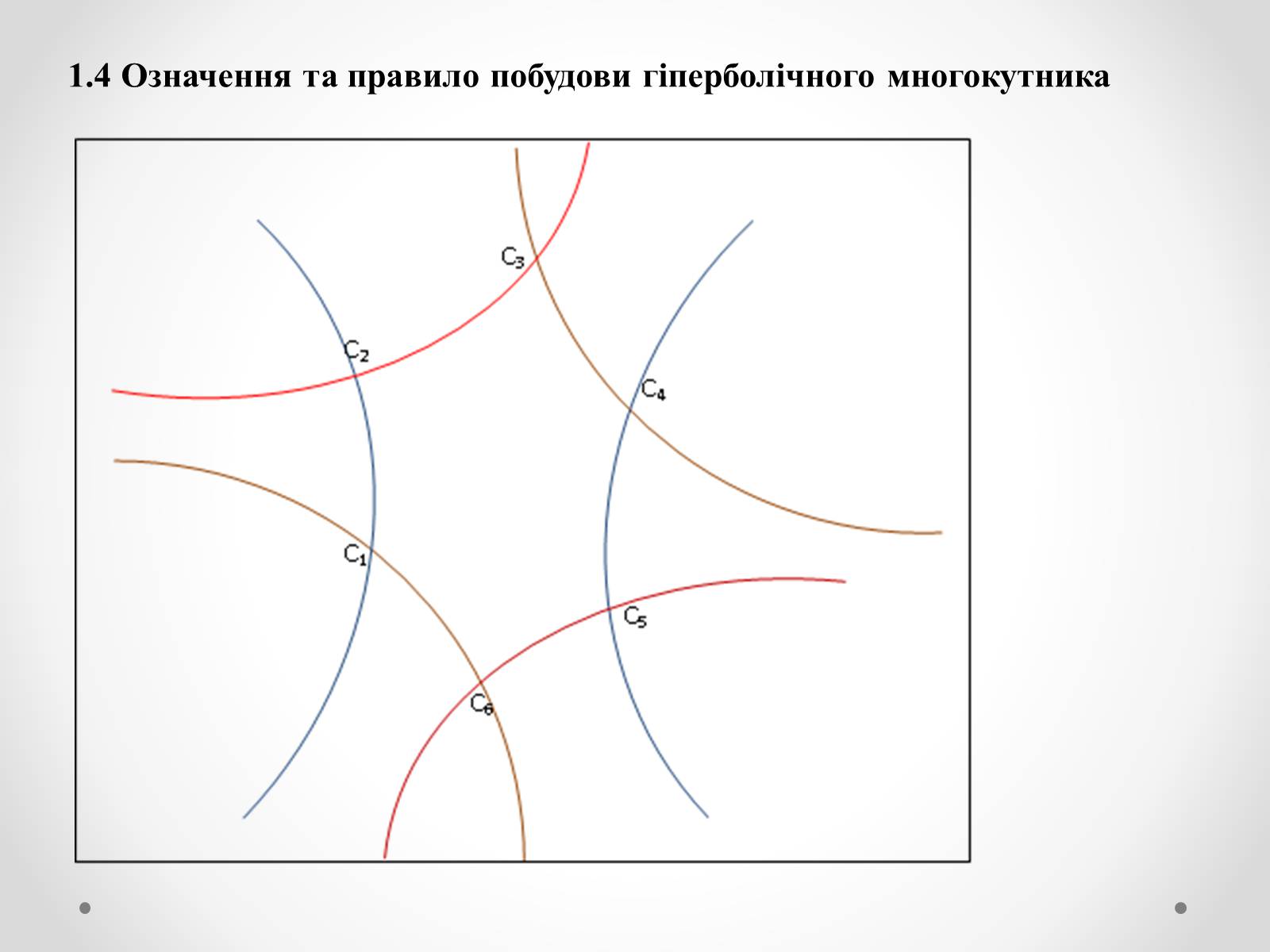
1.4 Означення та правило побудови гіперболічного многокутника
Слайд #7
1.5 Узагальнення многокутника з кривих ІІ порядку
Для побудови параболічного, еліптичного і гіперболічного 2n-кутників користуватимемося наступним правилом:
Будуємо n однойменних кривих так, щоб вони попарно перетинались (нагадаємо, що такі криві називаємо твірними);
Відмічаємо ті точки перетину пар побудованих кривих, що з'єднані частинами дуг твірних кривих, а протилежні частини дуг (сторони 2n-кутника) належать одній твірній кривій ІІ порядку;
2n-кутником з кривих ІІ порядку буде частина площини, обмежена відміченими точками, що з'єднуються цими частинами дуг.
Зауважимо: 2n-кутником з кривих ІІ порядку ми не будемо вважати той, який обмежений точками, що послідовно з'єднані частинами дуг довільних однойменних чи неоднойменних кривих ІІ порядку, тобто для побудови обов'язково потрібні твірні однойменні криві ІІ порядку.
Для побудови параболічного, еліптичного і гіперболічного 2n-кутників користуватимемося наступним правилом:
Будуємо n однойменних кривих так, щоб вони попарно перетинались (нагадаємо, що такі криві називаємо твірними);
Відмічаємо ті точки перетину пар побудованих кривих, що з'єднані частинами дуг твірних кривих, а протилежні частини дуг (сторони 2n-кутника) належать одній твірній кривій ІІ порядку;
2n-кутником з кривих ІІ порядку буде частина площини, обмежена відміченими точками, що з'єднуються цими частинами дуг.
Зауважимо: 2n-кутником з кривих ІІ порядку ми не будемо вважати той, який обмежений точками, що послідовно з'єднані частинами дуг довільних однойменних чи неоднойменних кривих ІІ порядку, тобто для побудови обов'язково потрібні твірні однойменні криві ІІ порядку.

Слайд #8
Розділ 2.
НЕТРАДИЦІЙНІ ВИДИ ЧОТИРИКУТНИКІВ
2.1 Означення опуклого параболічного чотирикутника та його властивості
2.2 Означення опуклого еліптичного чотирикутника та його властивості
2.3 Означення неопуклого гіперболічного чотирикутника та його властивості
НЕТРАДИЦІЙНІ ВИДИ ЧОТИРИКУТНИКІВ
2.1 Означення опуклого параболічного чотирикутника та його властивості
2.2 Означення опуклого еліптичного чотирикутника та його властивості
2.3 Означення неопуклого гіперболічного чотирикутника та його властивості

Слайд #9
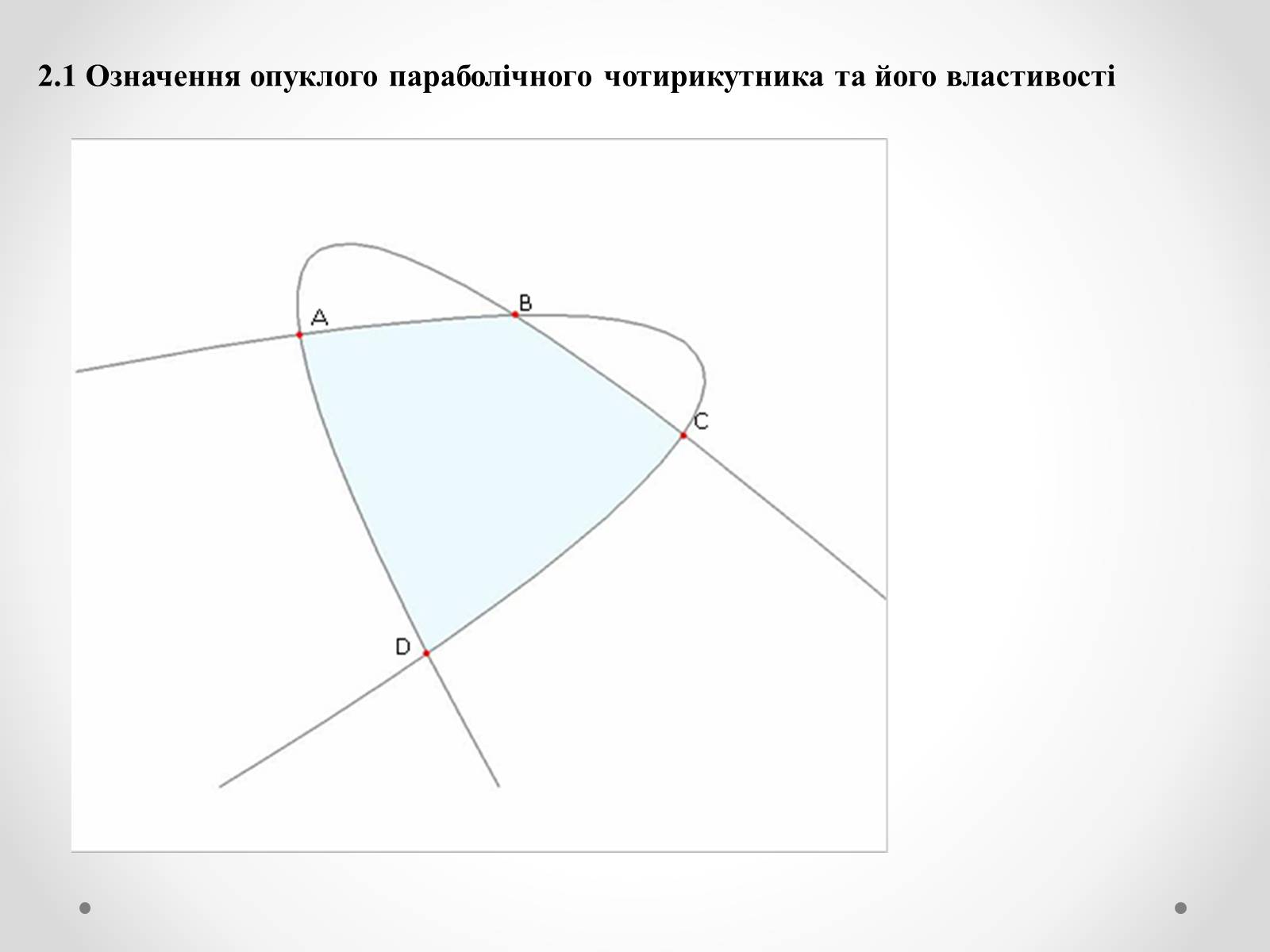
2.1 Означення опуклого параболічного чотирикутника та його властивості
Слайд #10
2.1 Означення опуклого параболічного чотирикутника та його властивості
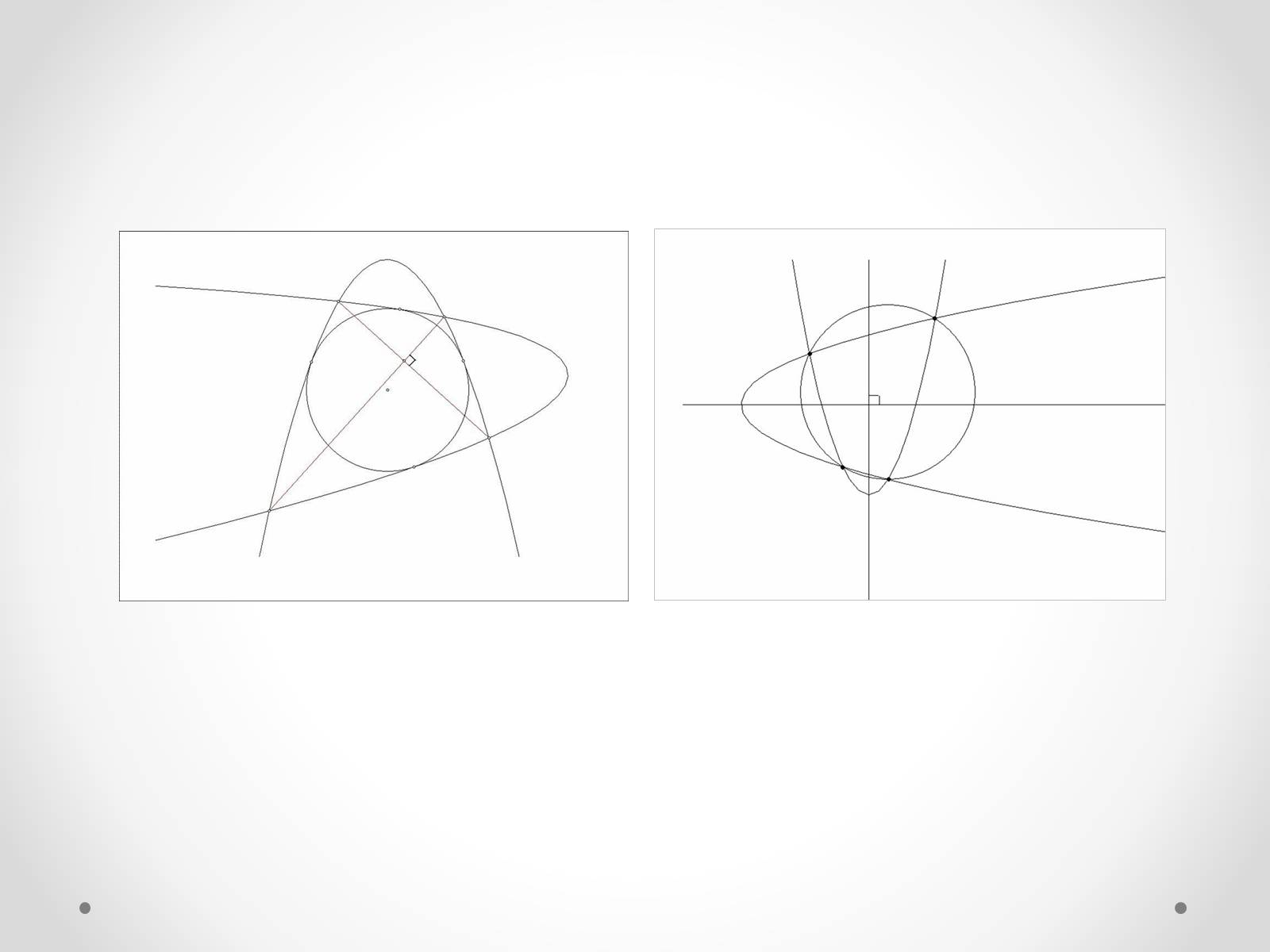
Слайд #11
2.1 Означення опуклого еліптичного чотирикутника та його властивості
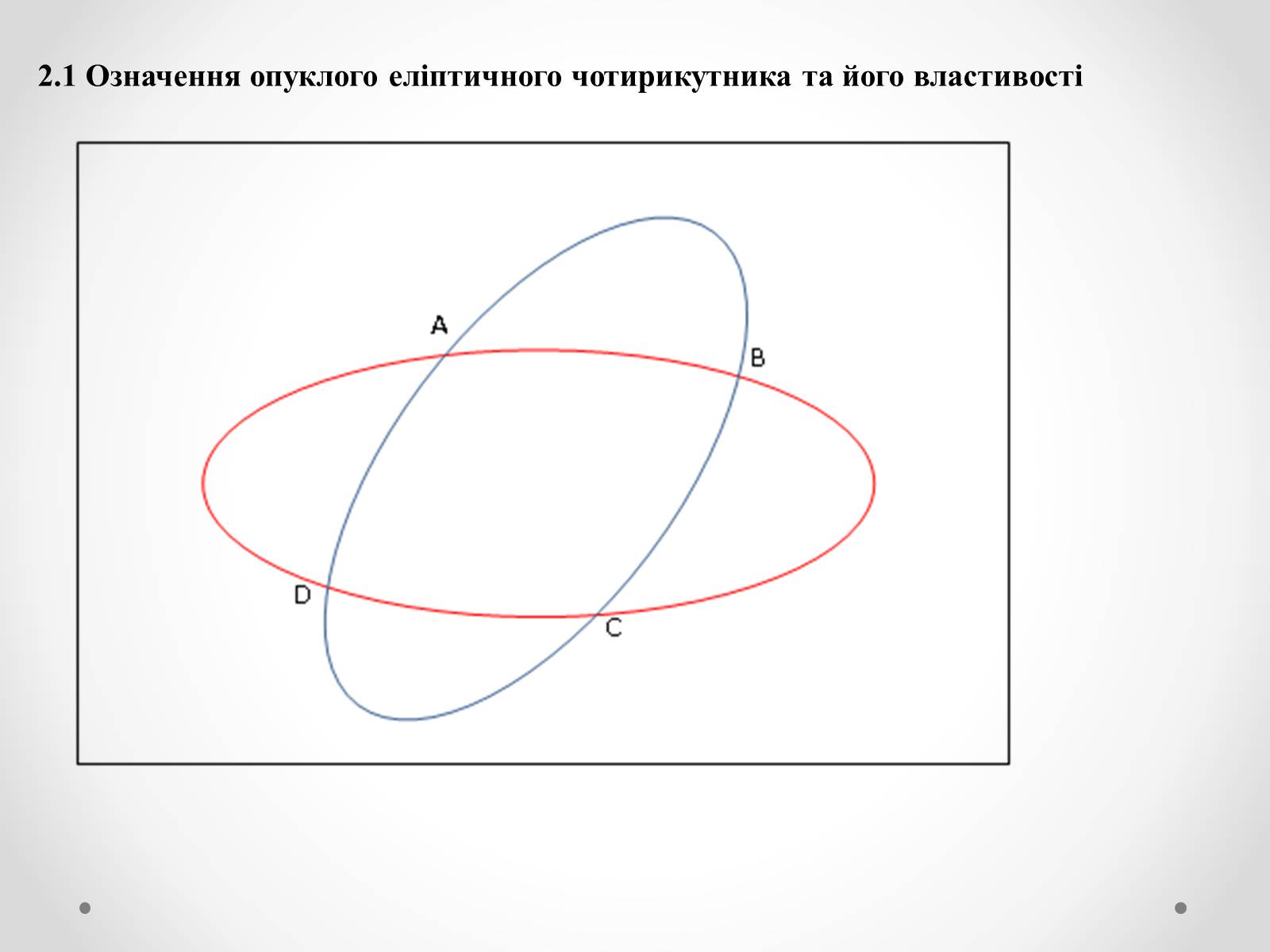
Слайд #12
2.1 Означення опуклого еліптичного чотирикутника та його властивості
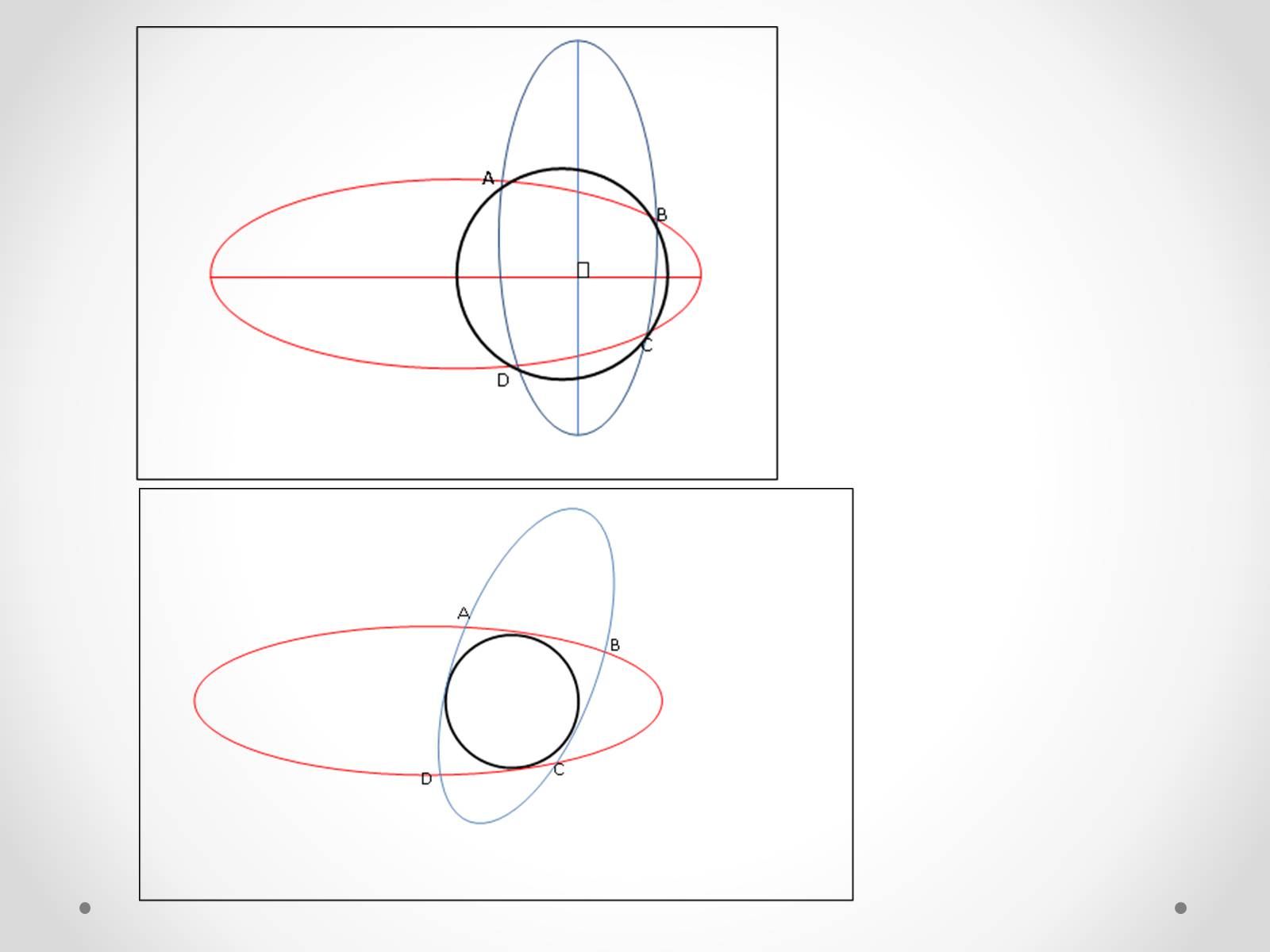
Слайд #13
2.1 Означення неопуклого гіперболічного чотирикутника та його властивості
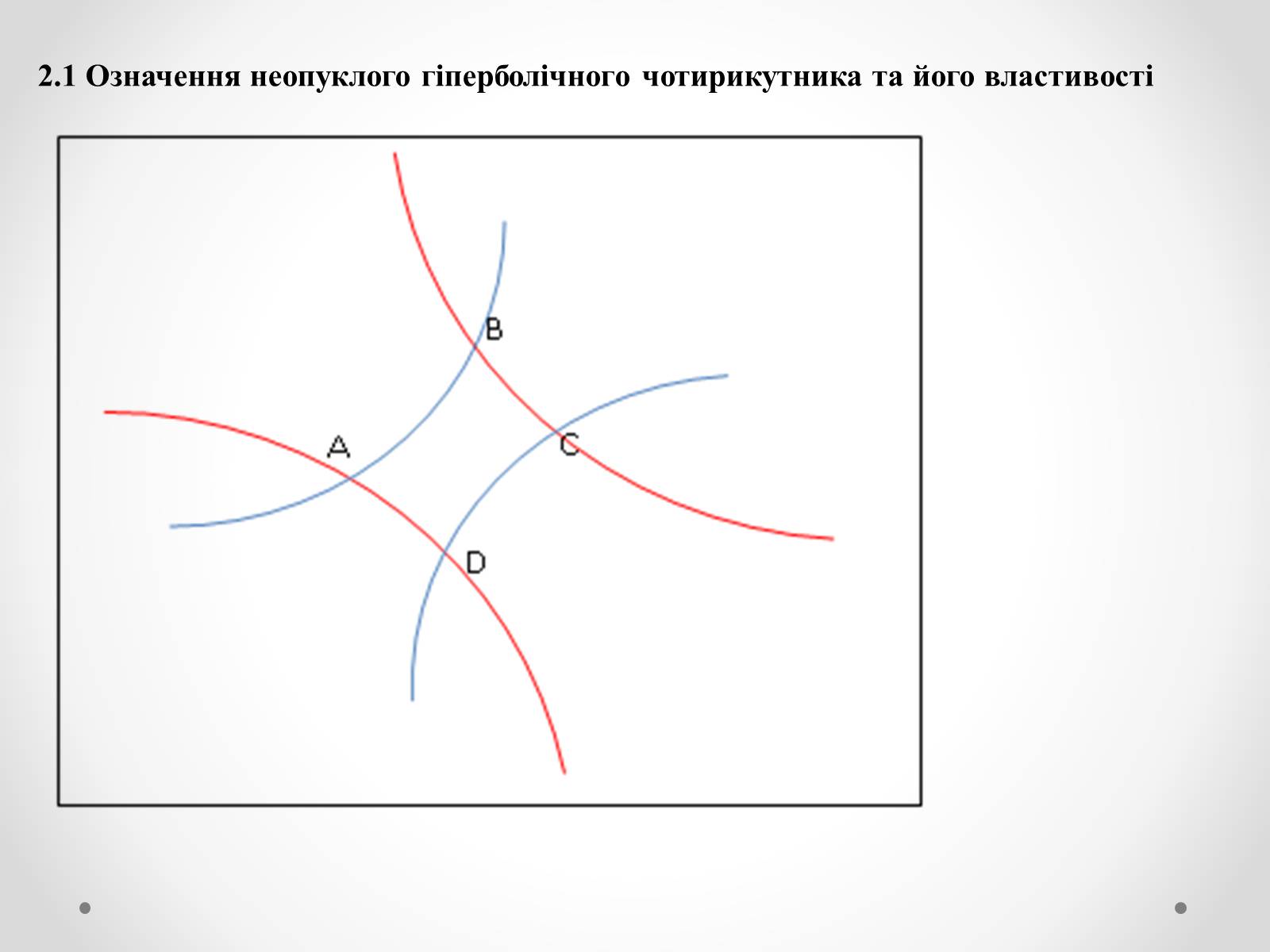
Слайд #14
2.1 Означення неопуклого гіперболічного чотирикутника та його властивості
Слайд #15
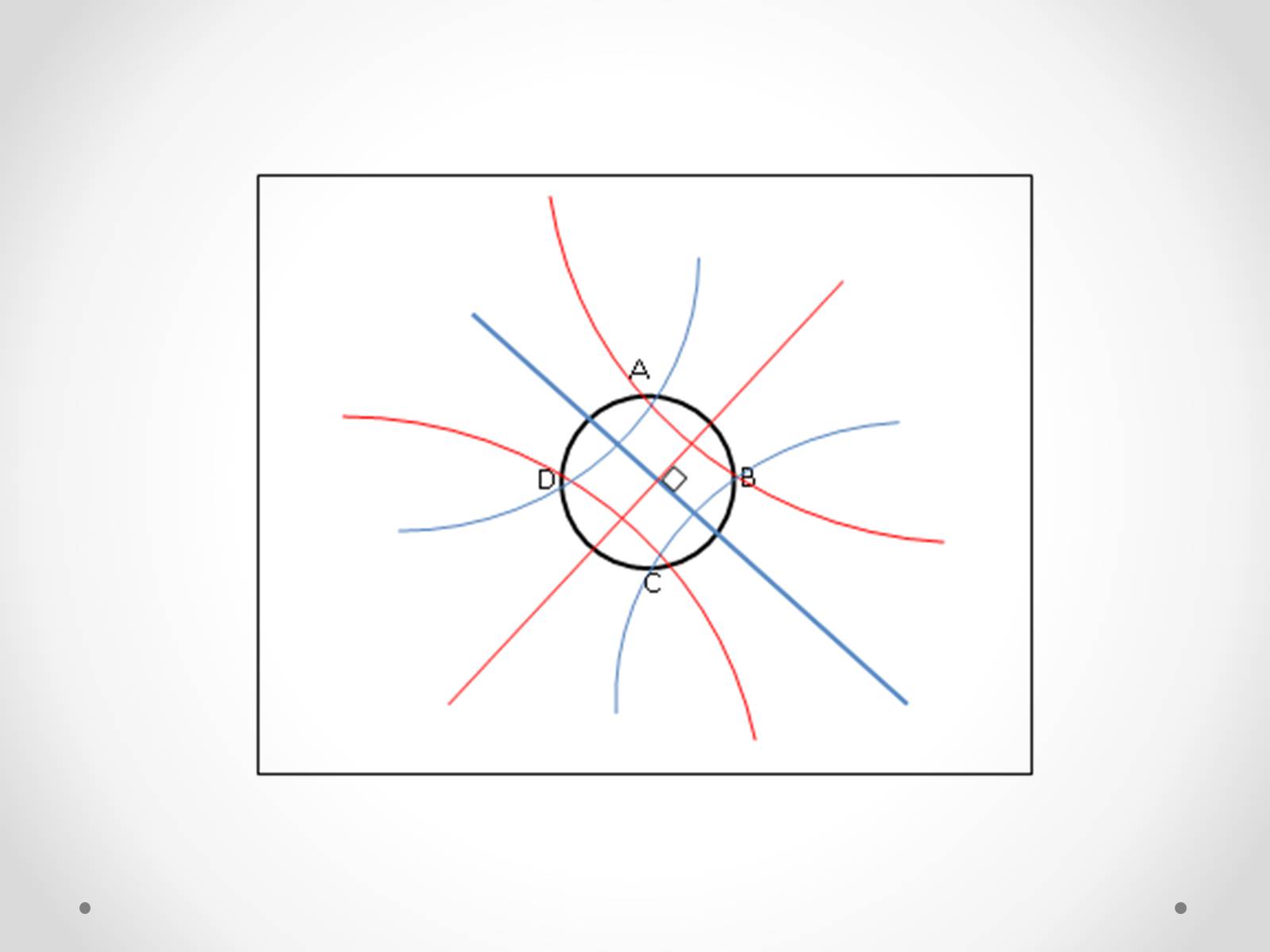
2.1 Означення неопуклого гіперболічного чотирикутника та його властивості
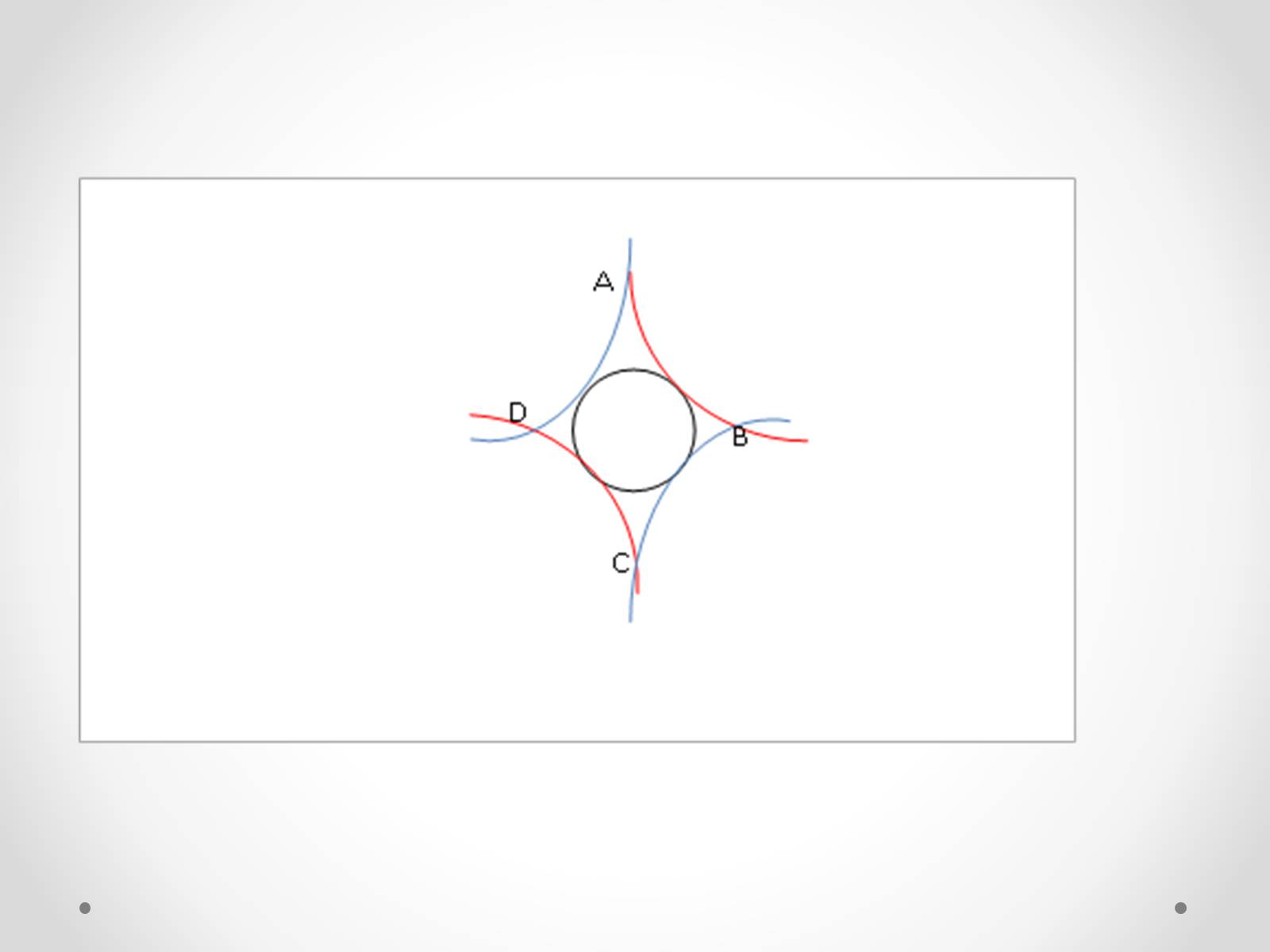
Слайд #16
2.4. Основні теореми
Теорема 1.
Параболічний чотирикутник описаний тоді і тільки тоді, коли його діагоналі перпендикулярні.
Теорема 1.
Параболічний чотирикутник описаний тоді і тільки тоді, коли його діагоналі перпендикулярні.

Слайд #17
Теорема 2.
Вершини параболічного (гіперболічного, еліптичного) чотирикутника лежать на одному колі тоді і тільки тоді, коли осі парабол (гіпербол, еліпсів) перпендикулярні.
Вершини параболічного (гіперболічного, еліптичного) чотирикутника лежать на одному колі тоді і тільки тоді, коли осі парабол (гіпербол, еліпсів) перпендикулярні.

Слайд #18
Гіпотеза.
Є гіпотеза, що для описаного еліптичного чотирикутника виконується таке твердження: суми довжин дуг протилежних криволінійних сторін рівні.
Є гіпотеза, що для описаного еліптичного чотирикутника виконується таке твердження: суми довжин дуг протилежних криволінійних сторін рівні.

Слайд #19
та
, то
Теорема 3.
Якщо твірні гіперболи задані формулами
гіперболічний чотирикутник описаний навколо кола радіуса R тоді і тільки тоді, коли
, причому
, то
Теорема 3.
Якщо твірні гіперболи задані формулами
гіперболічний чотирикутник описаний навколо кола радіуса R тоді і тільки тоді, коли
, причому

Слайд #20
Новизна і результати дослідження: визначено нові види чотирикутників, зокрема, параболічний, гіперболічний та еліптичний; досліджено питання щодо побудови таких чотирикутників; досліджено деякі їх властивості, які пов'язані з умовами вписаності в коло та описаності навколо кола.
У ході виконання роботи зроблено висновки:
- опрацьовано теорію класичних кривих ІІ порядку, на основі чого розглянуто многокутники, складені з дуг парабол, еліпсів, гіпербол;
- побудовано дещо новий вид чотирикутників, зокрема, параболічний, еліптичний, гіперболічний, сторони яких є частинами дуг класичних кривих ІІ порядку;
- сформульовані та доведені деякі основні властивості вищезгаданих фігур.
Практичне значення дослідження полягає в тому, що результати дослідження можна використовувати на факультативних заняттях з геометрії в загальноосвітніх навчальних закладах, а також на гурткових заняттях зі слухачами та кандидатами МАН.
Проведене дослідження не претендує на остаточне розв'язання поставленої проблеми, оскільки знайдено не всі властивості новостворених чотирикутників, і разом з тим ця робота дозволяє визначити деякі напрямки проведення подальших досліджень: створення подібним чином параболічних, еліптичних, гіперболічних n-кутників та встановлення їх основних властивостей; узагальнити поняття параболічного та еліптичного многокутника на поняття параболоїдного та еліпсоїдного многогранника і провести деякі їх дослідження.
У ході виконання роботи зроблено висновки:
- опрацьовано теорію класичних кривих ІІ порядку, на основі чого розглянуто многокутники, складені з дуг парабол, еліпсів, гіпербол;
- побудовано дещо новий вид чотирикутників, зокрема, параболічний, еліптичний, гіперболічний, сторони яких є частинами дуг класичних кривих ІІ порядку;
- сформульовані та доведені деякі основні властивості вищезгаданих фігур.
Практичне значення дослідження полягає в тому, що результати дослідження можна використовувати на факультативних заняттях з геометрії в загальноосвітніх навчальних закладах, а також на гурткових заняттях зі слухачами та кандидатами МАН.
Проведене дослідження не претендує на остаточне розв'язання поставленої проблеми, оскільки знайдено не всі властивості новостворених чотирикутників, і разом з тим ця робота дозволяє визначити деякі напрямки проведення подальших досліджень: створення подібним чином параболічних, еліптичних, гіперболічних n-кутників та встановлення їх основних властивостей; узагальнити поняття параболічного та еліптичного многокутника на поняття параболоїдного та еліпсоїдного многогранника і провести деякі їх дослідження.

Слайд #21
Дякую за увагу!
