- Головна
- Готові шкільні презентації
- Презентація на тему «Регресія. Інтерполяція. Екстраполяція»
Презентація на тему «Регресія. Інтерполяція. Екстраполяція»
233
Слайд #1
Регресія. Інтерполяція. Екстраполяція.

Слайд #2
План лекції
Вступ
Регресія
Лінійна
квадратична
Інтерполяція
Загальні відомості
Перша формула Ньютона
Друга формула Ньютона
Екстраполяція
Вступ
Регресія
Лінійна
квадратична
Інтерполяція
Загальні відомості
Перша формула Ньютона
Друга формула Ньютона
Екстраполяція

Слайд #3
Регресія
Задано сукупність показників y, що залежать від факторів х, то постає завдання знайти таку модель, яка б найкраще описувала існуючу залежність.
Одним з методів є регресійний аналіз. Регресія передбачає побудову такої Кривої, при якій значення показників, що лежать на ній будуть максимально наближені до фактичних, і продовжуючи цю криву одержуємо значення прогнозу.
Процес продовження прямої називається екстраполяцією. Відповідно до цього постає задача визначити цю пряму, тобто рівняння цієї прямої. В загальному вигляді рівняння прямої виглядає.
Задано сукупність показників y, що залежать від факторів х, то постає завдання знайти таку модель, яка б найкраще описувала існуючу залежність.
Одним з методів є регресійний аналіз. Регресія передбачає побудову такої Кривої, при якій значення показників, що лежать на ній будуть максимально наближені до фактичних, і продовжуючи цю криву одержуємо значення прогнозу.
Процес продовження прямої називається екстраполяцією. Відповідно до цього постає задача визначити цю пряму, тобто рівняння цієї прямої. В загальному вигляді рівняння прямої виглядає.

Слайд #4
Регресія
Задано сукупність показників y, що залежать від факторів х, то постає завдання знайти таку модель, яка б найкраще описувала існуючу залежність.
Одним з методів є регресійний аналіз. Регресія передбачає побудову такої Кривої, при якій значення показників, що лежать на ній будуть максимально наближені до фактичних, і продовжуючи цю криву одержуємо значення прогнозу.
Процес продовження прямої називається екстраполяцією. Відповідно до цього постає задача визначити цю пряму, тобто рівняння цієї прямої. В загальному вигляді рівняння прямої виглядає.
Задано сукупність показників y, що залежать від факторів х, то постає завдання знайти таку модель, яка б найкраще описувала існуючу залежність.
Одним з методів є регресійний аналіз. Регресія передбачає побудову такої Кривої, при якій значення показників, що лежать на ній будуть максимально наближені до фактичних, і продовжуючи цю криву одержуємо значення прогнозу.
Процес продовження прямої називається екстраполяцією. Відповідно до цього постає задача визначити цю пряму, тобто рівняння цієї прямої. В загальному вигляді рівняння прямої виглядає.
Слайд #5
Види Регресії

Слайд #6
Лінійна Регресія
Нехай задано статистичні дані у вигляді таблиці і відповідності кожному значенню x значення y (y = f(x))
X1
X2
…
Xn-1
Xn
y1
Y2
…
Yn-1
Yn
Припустимо, що невідома функція є лінійною, тоді y = ax+b ,де a і b невідомі параметри.
Нехай задано статистичні дані у вигляді таблиці і відповідності кожному значенню x значення y (y = f(x))
X1
X2
…
Xn-1
Xn
y1
Y2
…
Yn-1
Yn
Припустимо, що невідома функція є лінійною, тоді y = ax+b ,де a і b невідомі параметри.

Слайд #7
Лінійна Регресія (2)

Слайд #8
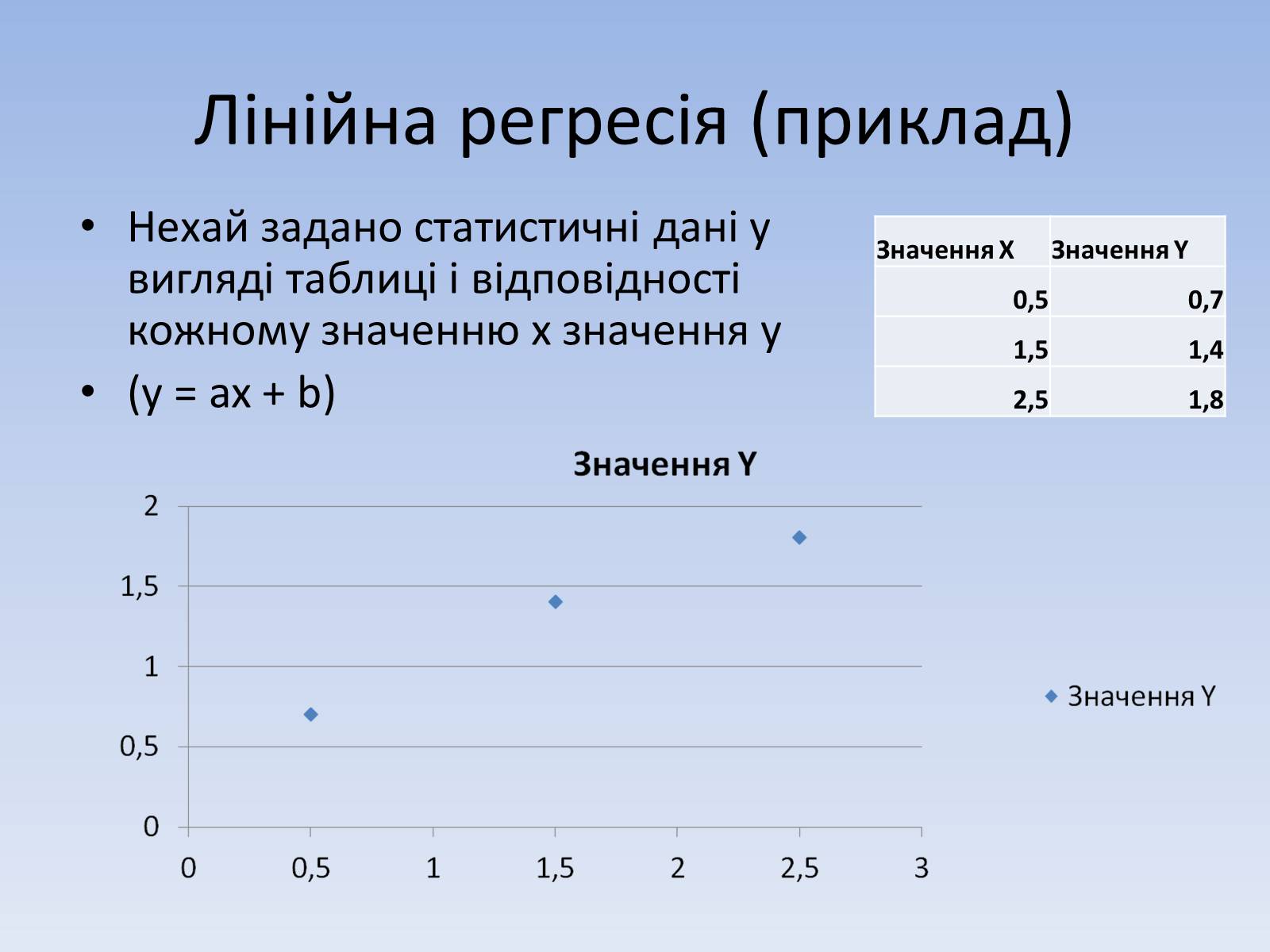
Лінійна регресія (приклад)
Значення X
Значення Y
0,5
0,7
1,5
1,4
2,5
1,8
Нехай задано статистичні дані у вигляді таблиці і відповідності кожному значенню x значення y
(y = ax + b)
Значення X
Значення Y
0,5
0,7
1,5
1,4
2,5
1,8
Нехай задано статистичні дані у вигляді таблиці і відповідності кожному значенню x значення y
(y = ax + b)
Слайд #9
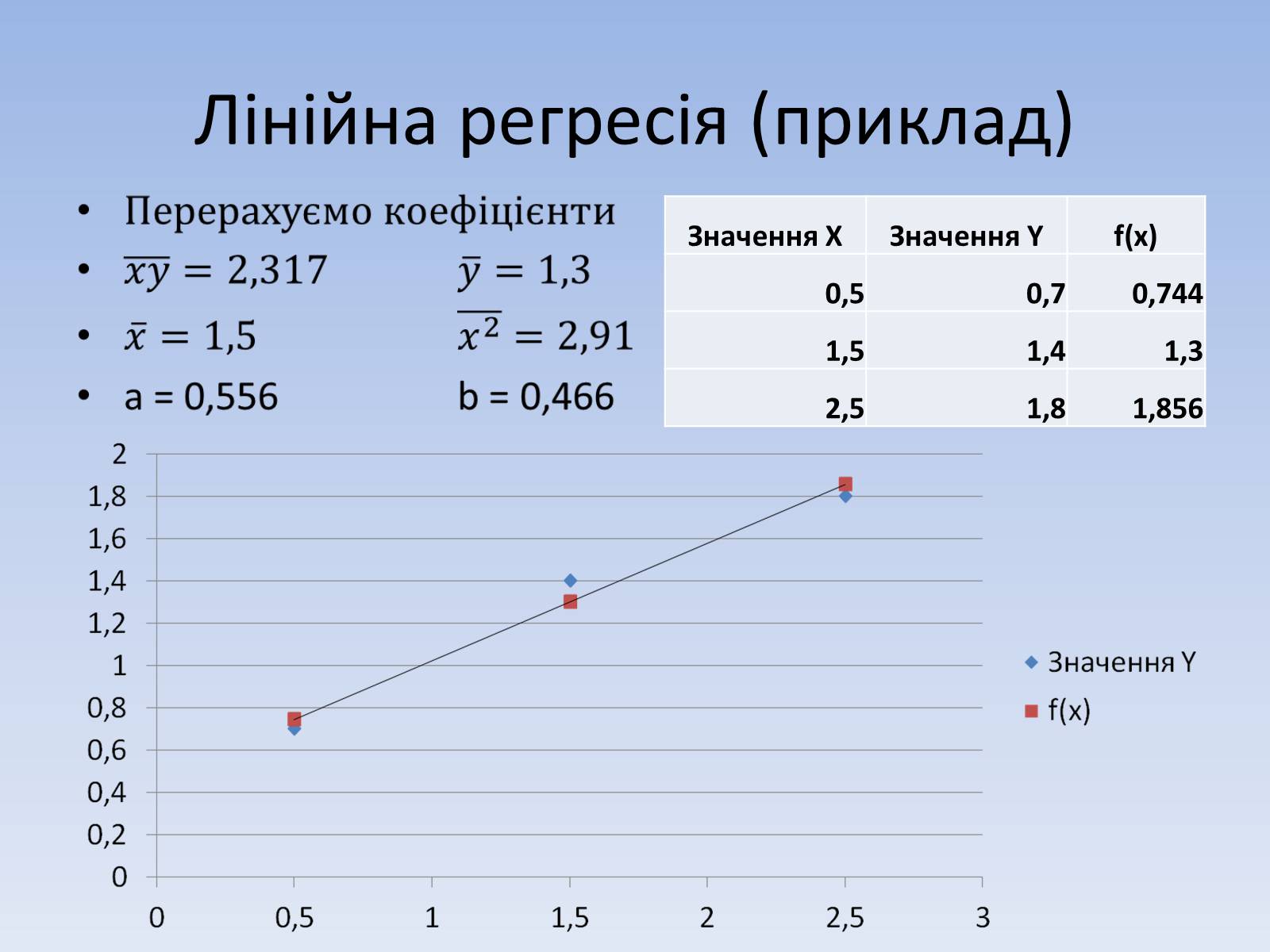
Лінійна регресія (приклад)
Значення X
Значення Y
f(x)
0,5
0,7
0,744
1,5
1,4
1,3
2,5
1,8
1,856
Значення X
Значення Y
f(x)
0,5
0,7
0,744
1,5
1,4
1,3
2,5
1,8
1,856
Слайд #10
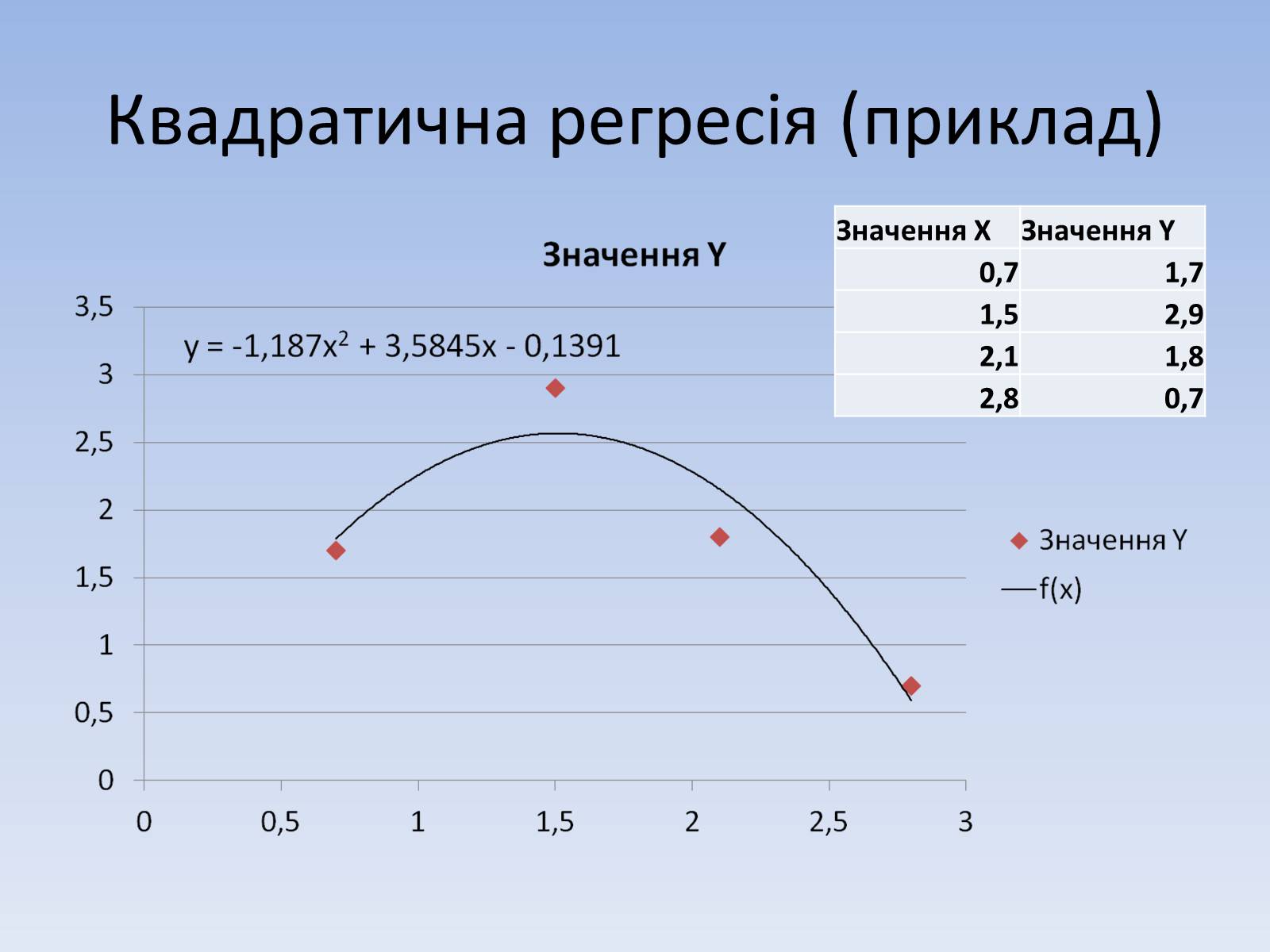
Квадратична регресія
Припустимо, що невідома функція є квадратичною, тоді
y = a+bx+cx^2 ,де a, b і c невідомі параметри.
Припустимо, що невідома функція є квадратичною, тоді
y = a+bx+cx^2 ,де a, b і c невідомі параметри.

Слайд #11
Квадратична регресія (приклад)
Значення X
Значення Y
0,7
1,7
1,5
2,9
2,1
1,8
2,8
0,7
Значення X
Значення Y
0,7
1,7
1,5
2,9
2,1
1,8
2,8
0,7
Слайд #12
Квадратична регресія (приклад)
Значення X
Значення Y
0,7
1,7
1,5
2,9
2,1
1,8
2,8
0,7
Значення X
Значення Y
0,7
1,7
1,5
2,9
2,1
1,8
2,8
0,7
Слайд #13
Інтерполяція
Припустимо відомо значення деякої функції f в n+1 різних точках x0,x1,…,xn які позначимо наступним способом
fi = f(xi) i=0,1,..,n
Такі дані зазвичай отримують з експериментів чи за допомогою складних обчислень. Зазвичай виникає задача наближеного встановлення функції f в будь-якій точці x.
Наближене встановлення функції f називається інтерполяцією функції.
Часто для розв'язування цієї задачі будують алгебраїчний многочлен Ln(x) степені n, який в точках xi приймає задані значення fi = Ln(xi).
Ln(x)=a0xn+a1xn-1+a2xn-2+...+an-1x+an такий многочлен називається інтерполяційними многчленом.
Точки xi i=0,1,..,n називаються вузлами інтерполяції.
Припустимо відомо значення деякої функції f в n+1 різних точках x0,x1,…,xn які позначимо наступним способом
fi = f(xi) i=0,1,..,n
Такі дані зазвичай отримують з експериментів чи за допомогою складних обчислень. Зазвичай виникає задача наближеного встановлення функції f в будь-якій точці x.
Наближене встановлення функції f називається інтерполяцією функції.
Часто для розв'язування цієї задачі будують алгебраїчний многочлен Ln(x) степені n, який в точках xi приймає задані значення fi = Ln(xi).
Ln(x)=a0xn+a1xn-1+a2xn-2+...+an-1x+an такий многочлен називається інтерполяційними многчленом.
Точки xi i=0,1,..,n називаються вузлами інтерполяції.

Слайд #14
Інтерполяція(2)

Слайд #15
Інтерполяційний многочлен Ньютона для рівновіддалених вузлів
Часто інтерполяція ведеться для функції, заданих таблицями з рівно віддаленими значеннями аргументів.
Для таких таблиць побудова інтерполяційних формул спрощується.
Часто інтерполяція ведеться для функції, заданих таблицями з рівно віддаленими значеннями аргументів.
Для таких таблиць побудова інтерполяційних формул спрощується.
Слайд #16
скінченні різниці

Слайд #17
Перша Інтерполяційна формула Ньютона
Нехай будемо шукати інтерполяційний многочлен у вигляді
Pn(x)=a0+a1(x-x0)+a2(x-x0)(x-x1)+...+an(x-x0)(x-x1)...(x-xn-1)
Найдем значення коефіцієнтів a0, a1, a2, ...,an:
Припустивши, що x=x0, знаходимо a0=P(x0)=y0;
Далі подставляючи значення x1, x2, ...,xn отримуємо:
a1=Δy0/h, де h= xi+1-xi
a2=Δ2y0/2!h2
a3=Δ3y0/3!h3
....................
an=Δny0/n!hn
В кінцевому результаті отримуємо многочлен:Pn(x)=y0+ Δy0/h*(x-x0)+ Δ2y0/2!h2*(x-x0)(x-x1)+...+ Δny0/n!hn*(x-x0)(x-x1)...(x-xn-1) (1)
Практично формула (1) застосовується в іншому вигляді:
Візьмемо: t=(x-x0)/h, тоді x=x0+th и формула (1) перетворюється на:
Pn(x)=y0+tΔy0+t(t-1)/2! Δ2y0+...+t(t-1)...(t-n+1)/n!Δny0 (2)
Формула (2) називається інтерполяційной формулой Ньютона.
Нехай будемо шукати інтерполяційний многочлен у вигляді
Pn(x)=a0+a1(x-x0)+a2(x-x0)(x-x1)+...+an(x-x0)(x-x1)...(x-xn-1)
Найдем значення коефіцієнтів a0, a1, a2, ...,an:
Припустивши, що x=x0, знаходимо a0=P(x0)=y0;
Далі подставляючи значення x1, x2, ...,xn отримуємо:
a1=Δy0/h, де h= xi+1-xi
a2=Δ2y0/2!h2
a3=Δ3y0/3!h3
....................
an=Δny0/n!hn
В кінцевому результаті отримуємо многочлен:Pn(x)=y0+ Δy0/h*(x-x0)+ Δ2y0/2!h2*(x-x0)(x-x1)+...+ Δny0/n!hn*(x-x0)(x-x1)...(x-xn-1) (1)
Практично формула (1) застосовується в іншому вигляді:
Візьмемо: t=(x-x0)/h, тоді x=x0+th и формула (1) перетворюється на:
Pn(x)=y0+tΔy0+t(t-1)/2! Δ2y0+...+t(t-1)...(t-n+1)/n!Δny0 (2)
Формула (2) називається інтерполяційной формулой Ньютона.

Слайд #18
http://numericalmethods.eng.usf.edu
18
Приклад
Швидкість підйому ракети задана, як функція від часу в таблиці 1.
Знайти швидкість підйому ракети в момент часу t=16 секунд використовуючи метод Ньютона квадратичної інтерполяції.
t
v(t)
s
m/s
10
227.04
15
362.78
20
517.35
22.5
602.97
30
901.67
Таблиця 1. Швидкість, як функція від часу
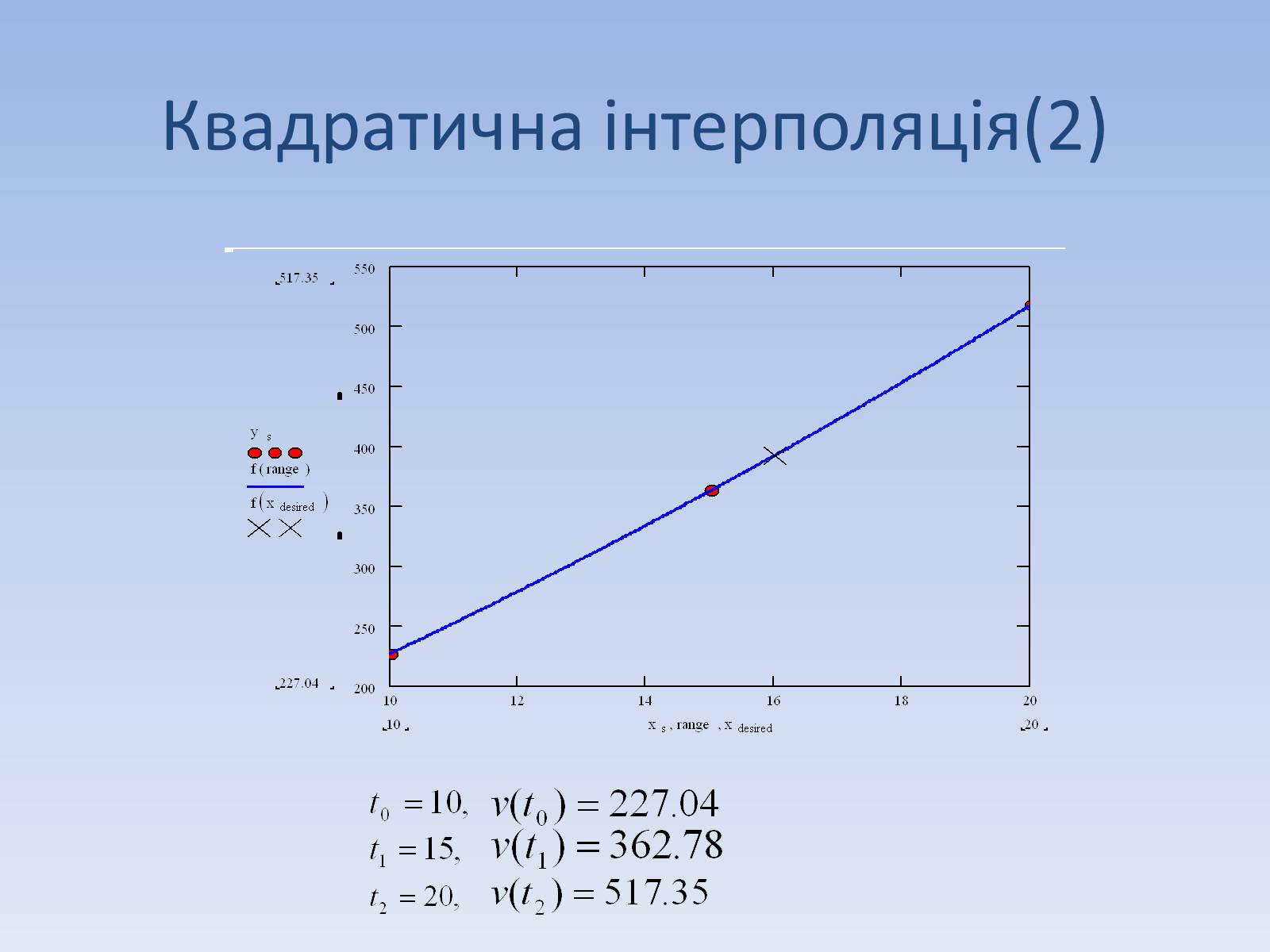
Figure 2: залежність швидкості від часу
18
Приклад
Швидкість підйому ракети задана, як функція від часу в таблиці 1.
Знайти швидкість підйому ракети в момент часу t=16 секунд використовуючи метод Ньютона квадратичної інтерполяції.
t
v(t)
s
m/s
10
227.04
15
362.78
20
517.35
22.5
602.97
30
901.67
Таблиця 1. Швидкість, як функція від часу
Figure 2: залежність швидкості від часу

Слайд #19
Квадратична інтерполяція(2)
Слайд #20
Квадратична інтерполяція(3)

Слайд #21
Квадратична інтерполяція(4)
Перепишемо
Перепишемо

Слайд #22
Друга інтерполяційна формула Ньютона

Слайд #23
Дякую за увагу!
