- Головна
- Готові шкільні презентації
- Презентація на тему «Многогранники» (варіант 2)
Презентація на тему «Многогранники» (варіант 2)
278
Слайд #1
Многогранники

Слайд #2
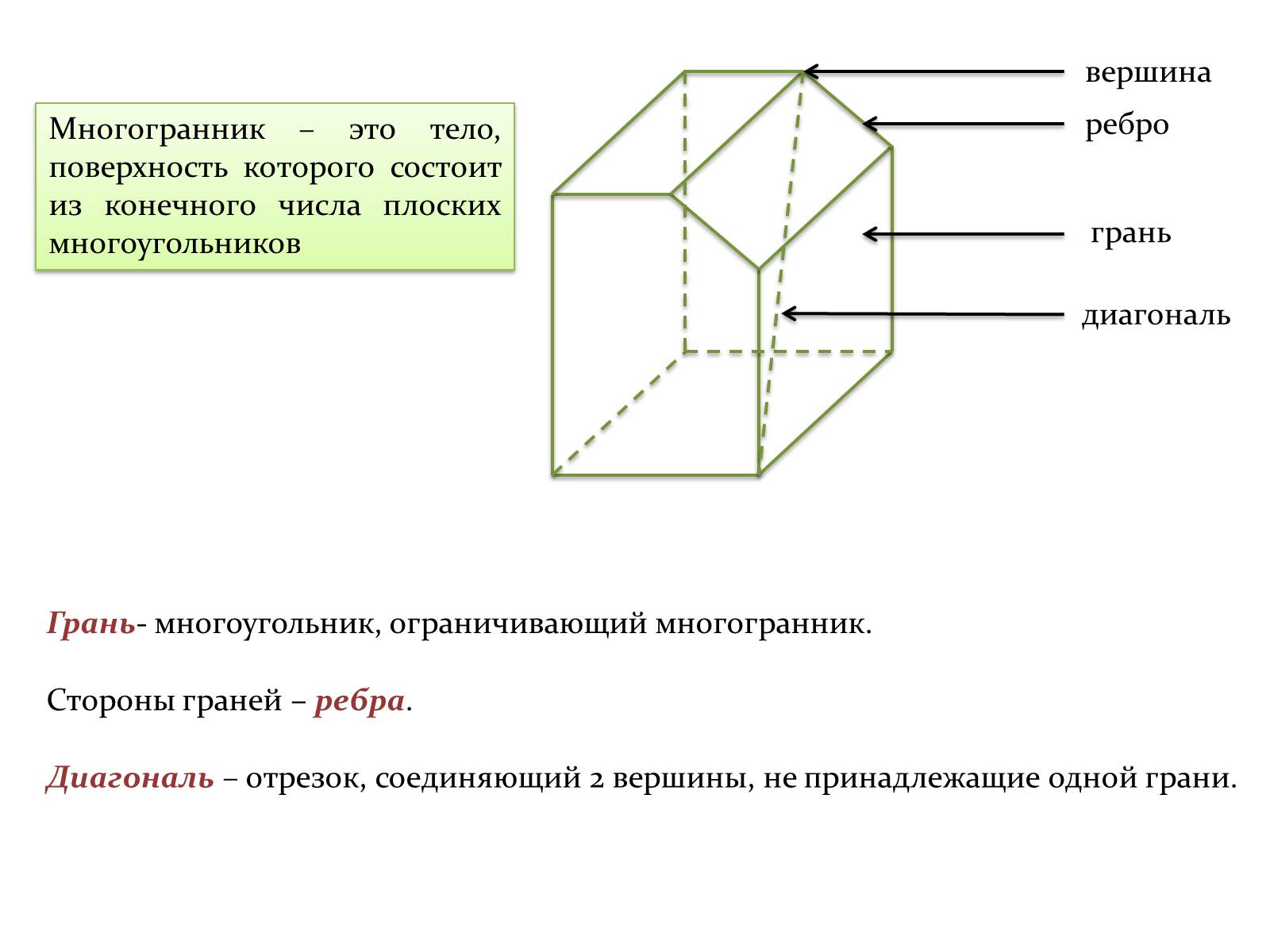
Многогранник – это тело, поверхность которого состоит из конечного числа плоских многоугольников
вершина
ребро
грань
диагональ
Грань- многоугольник, ограничивающий многогранник.
Стороны граней – ребра.
Диагональ – отрезок, соединяющий 2 вершины, не принадлежащие одной грани.
вершина
ребро
грань
диагональ
Грань- многоугольник, ограничивающий многогранник.
Стороны граней – ребра.
Диагональ – отрезок, соединяющий 2 вершины, не принадлежащие одной грани.
Слайд #3
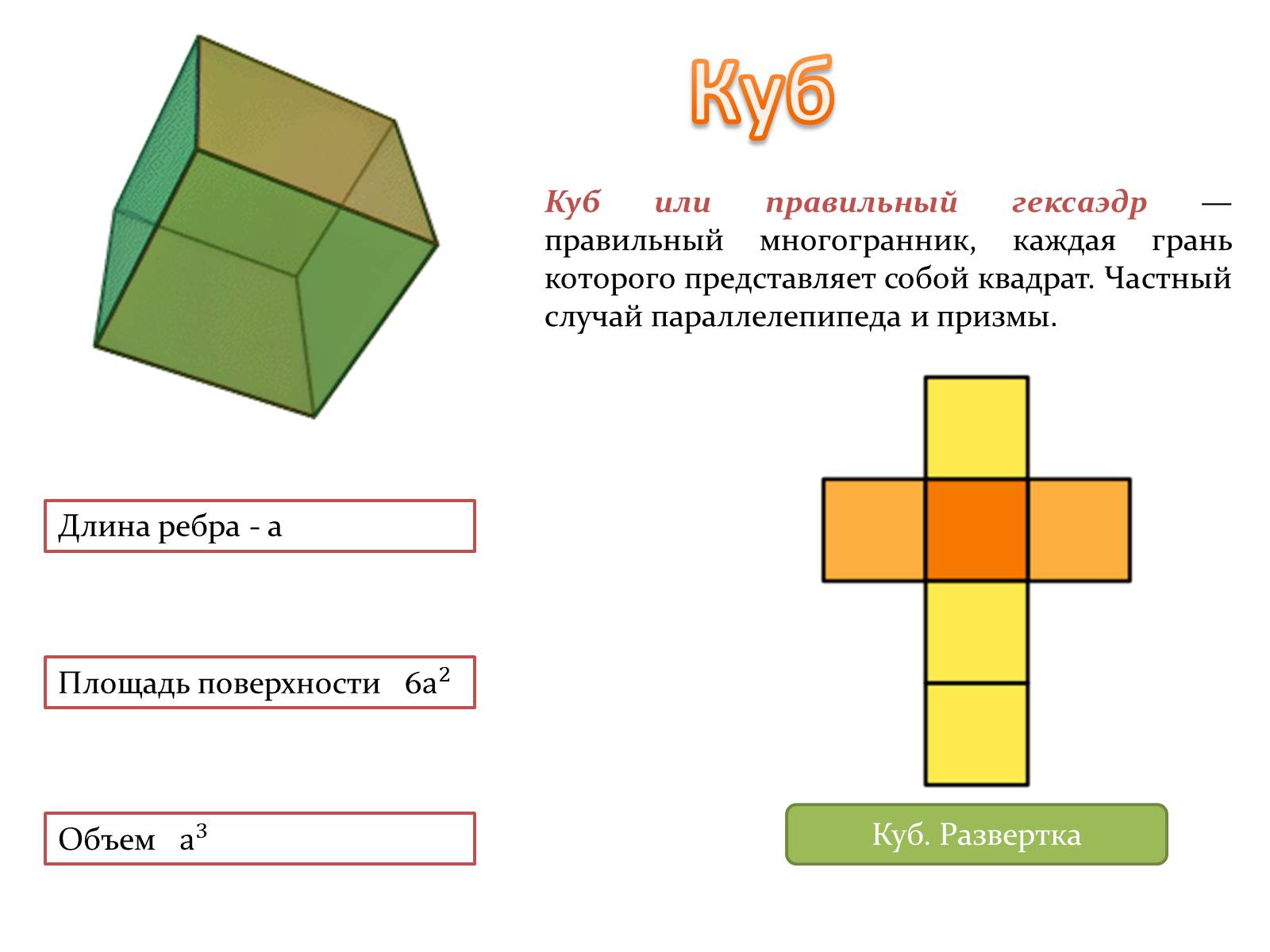
Куб
Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.
Куб. Развертка
Длина ребра - а
Площадь поверхности 6
Объем
Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.
Куб. Развертка
Длина ребра - а
Площадь поверхности 6
Объем
Слайд #4
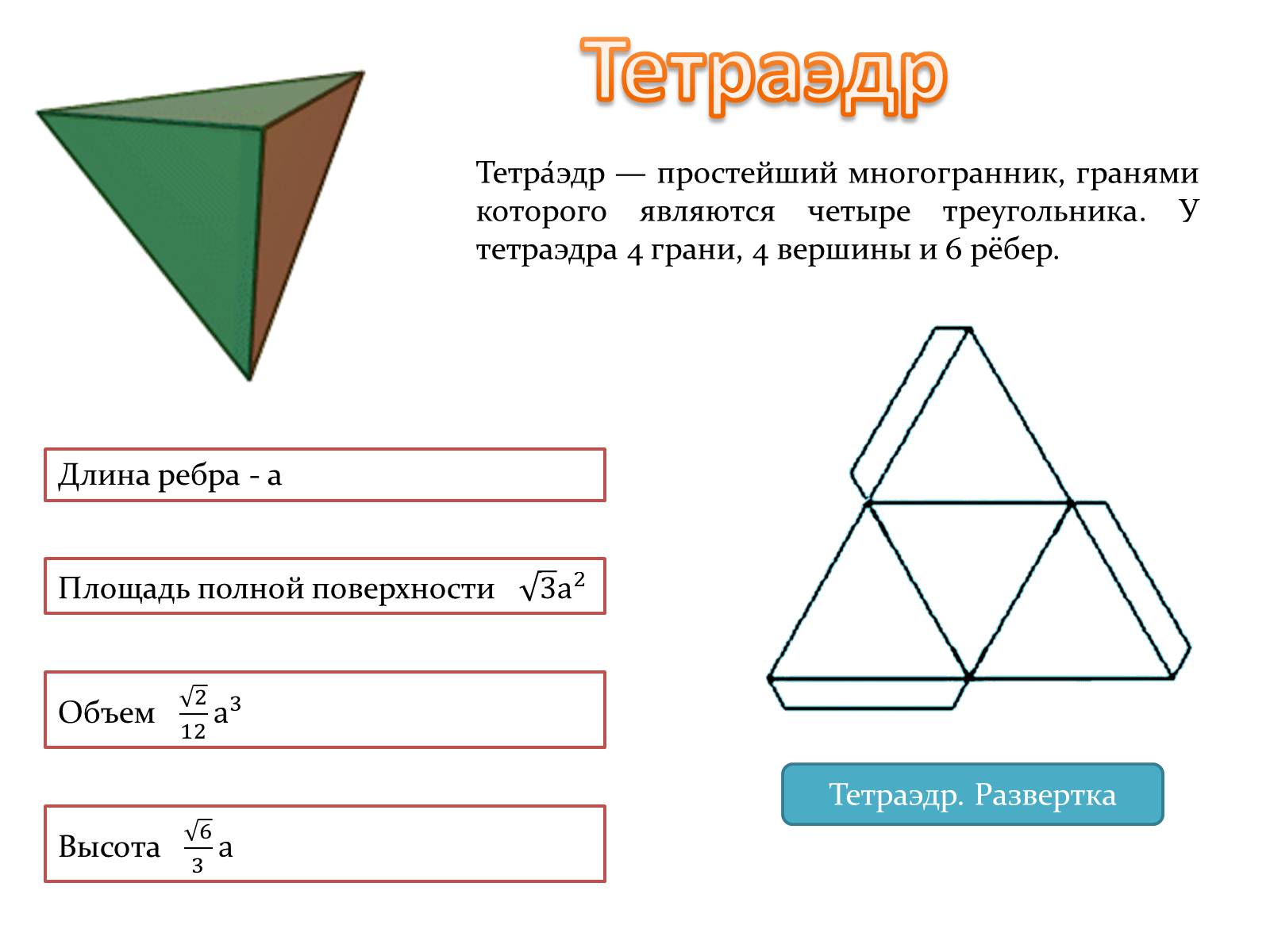
Тетраэдр
Тетра́эдр — простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Тетраэдр. Развертка
Длина ребра - а
Площадь полной поверхности
Объем
Высота
Тетра́эдр — простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Тетраэдр. Развертка
Длина ребра - а
Площадь полной поверхности
Объем
Высота
Слайд #5
Тетраэдры в природе и технике
Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.

Слайд #6
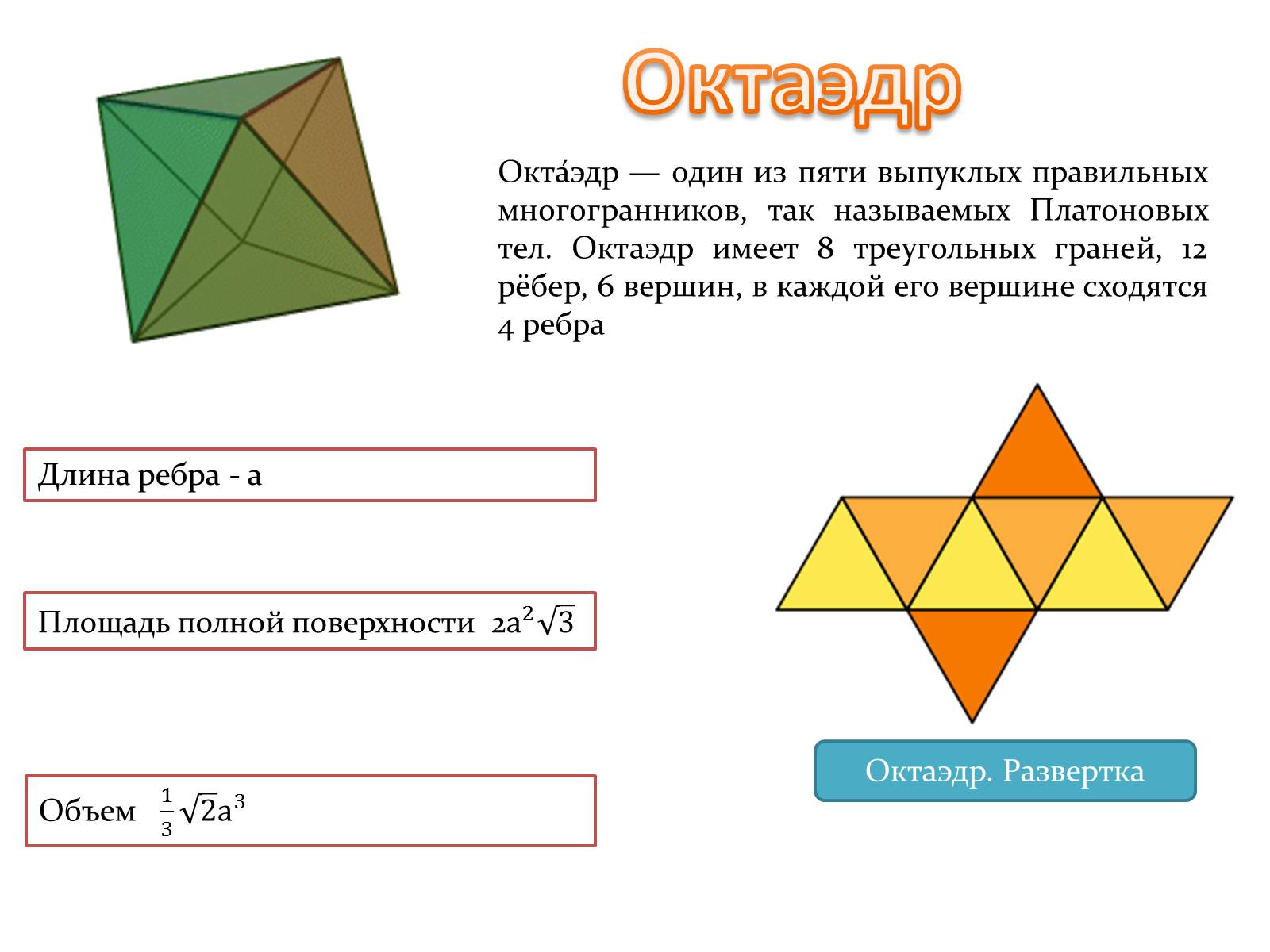
Октаэдр
Окта́эдр — один из пяти выпуклых правильных многогранников, так называемых Платоновых тел. Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра
Длина ребра - а
Площадь полной поверхности 2
Объем
Октаэдр. Развертка
Окта́эдр — один из пяти выпуклых правильных многогранников, так называемых Платоновых тел. Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра
Длина ребра - а
Площадь полной поверхности 2
Объем
Октаэдр. Развертка
Слайд #7
Октаэдры в природе
Многие природные кубические кристаллы имеют форму октаэдра. Это алмаз, хлорид натрия, перовскит, оливин, флюорит, шпинель.
Форму октаэдра имеют межатомные пустоты (поры) в плотноупакованных структурах чистых металлов (никеле, меди, магнии, титане, лантане и многих других) и ионных соединений (хлорид натрия, сфалерит, вюрцит и др.).
Многие природные кубические кристаллы имеют форму октаэдра. Это алмаз, хлорид натрия, перовскит, оливин, флюорит, шпинель.
Форму октаэдра имеют межатомные пустоты (поры) в плотноупакованных структурах чистых металлов (никеле, меди, магнии, титане, лантане и многих других) и ионных соединений (хлорид натрия, сфалерит, вюрцит и др.).

Слайд #8
Икосаэдр
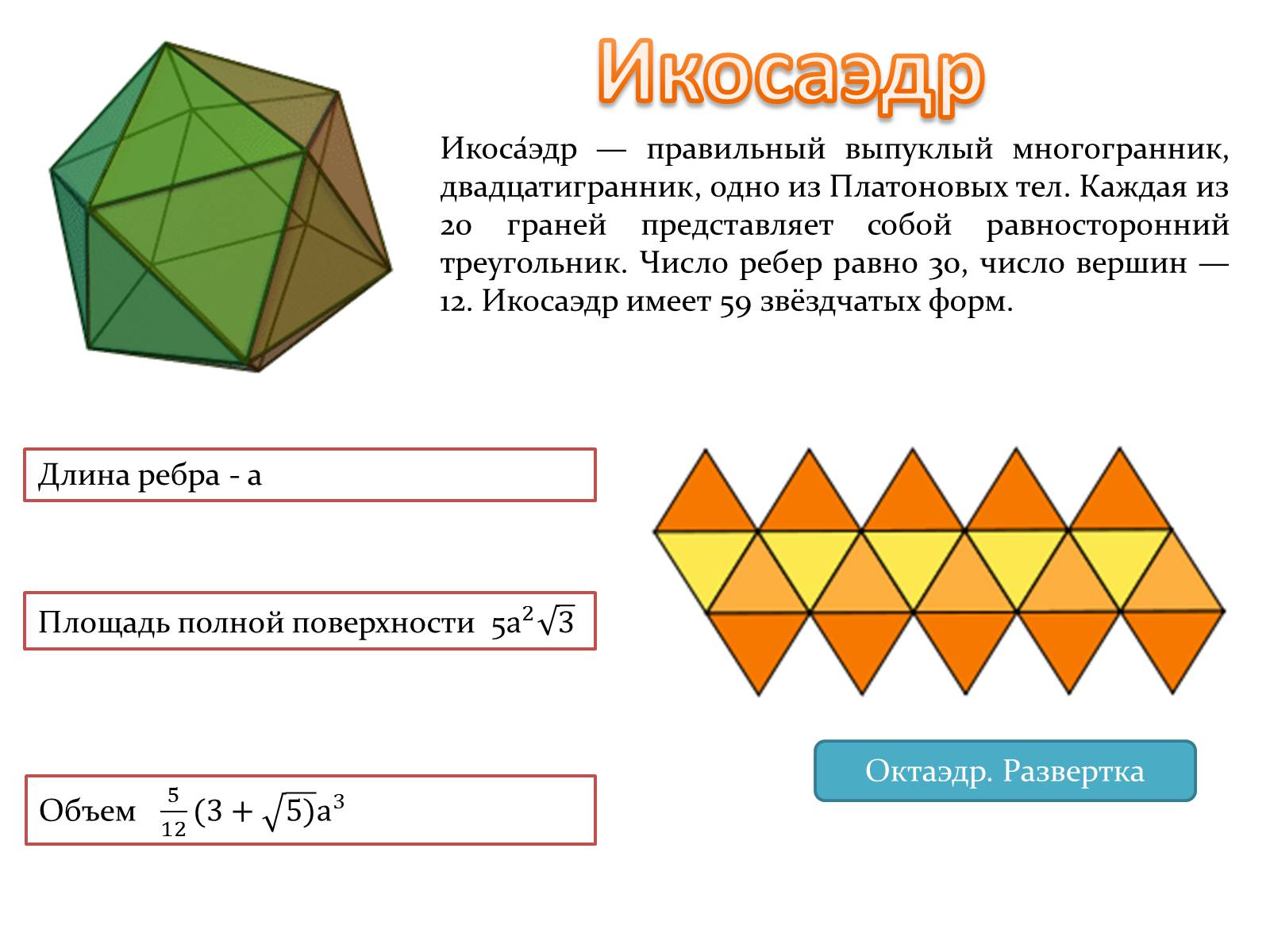
Октаэдр. Развертка
Длина ребра - а
Площадь полной поверхности 5
Объем
Икоса́эдр — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.
Октаэдр. Развертка
Длина ребра - а
Площадь полной поверхности 5
Объем
Икоса́эдр — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.
Слайд #9
Додекаэдр
Додека́эдр — двенадцатигранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней, 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).
Площадь полной поверхности 3 )
Объем
Длина ребра - а
Додекаэдр. Развертка
Додека́эдр — двенадцатигранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней, 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).
Площадь полной поверхности 3 )
Объем
Длина ребра - а
Додекаэдр. Развертка

Слайд #10
Презентацию выполнила:
ученица 11-А класса
Алчевской ИТГ
Чернявская Карина
ученица 11-А класса
Алчевской ИТГ
Чернявская Карина
