- Головна
- Готові шкільні презентації
- Презентація на тему «Ґотфрід Лейбніц у сфері математики і філософії»
Презентація на тему «Ґотфрід Лейбніц у сфері математики і філософії»
345
Слайд #1
Ґотфрід Лейбніц у сфері математики і філософії
Підготували:
Антонюк Устина
Купчак Ярина
Класична гімназія
11-Б клас
Підготували:
Антонюк Устина
Купчак Ярина
Класична гімназія
11-Б клас

Слайд #2
ПЛАН
Біографія Ґотфріда Лейбніца
Лейбніц у математиці
Лейбніц у філософії
Висновок
Біографія Ґотфріда Лейбніца
Лейбніц у математиці
Лейбніц у філософії
Висновок

Слайд #3
Ґотфрід Вільгельм Лейбніц(1 липня 1646, Лейпциг — 14 листопада 1716, Ганновер)
Провідний німецький філософ, логік, математик, фізик, мовознавець та дипломат.
Передбачив принципи сучасної комбінаторики. Створив першу механічну лічильну машину, здатну виконувати додавання, віднімання, множення й ділення. Незалежно від Ньютона створив диференціальне й інтегральне числення і заклав основи двійкової системи числення.
Провідний німецький філософ, логік, математик, фізик, мовознавець та дипломат.
Передбачив принципи сучасної комбінаторики. Створив першу механічну лічильну машину, здатну виконувати додавання, віднімання, множення й ділення. Незалежно від Ньютона створив диференціальне й інтегральне числення і заклав основи двійкової системи числення.

Слайд #4
Математика
Свої успіхи у математиці Лейбніц розпочинає із дослідження теорії рядів та виведення такої формули . . .
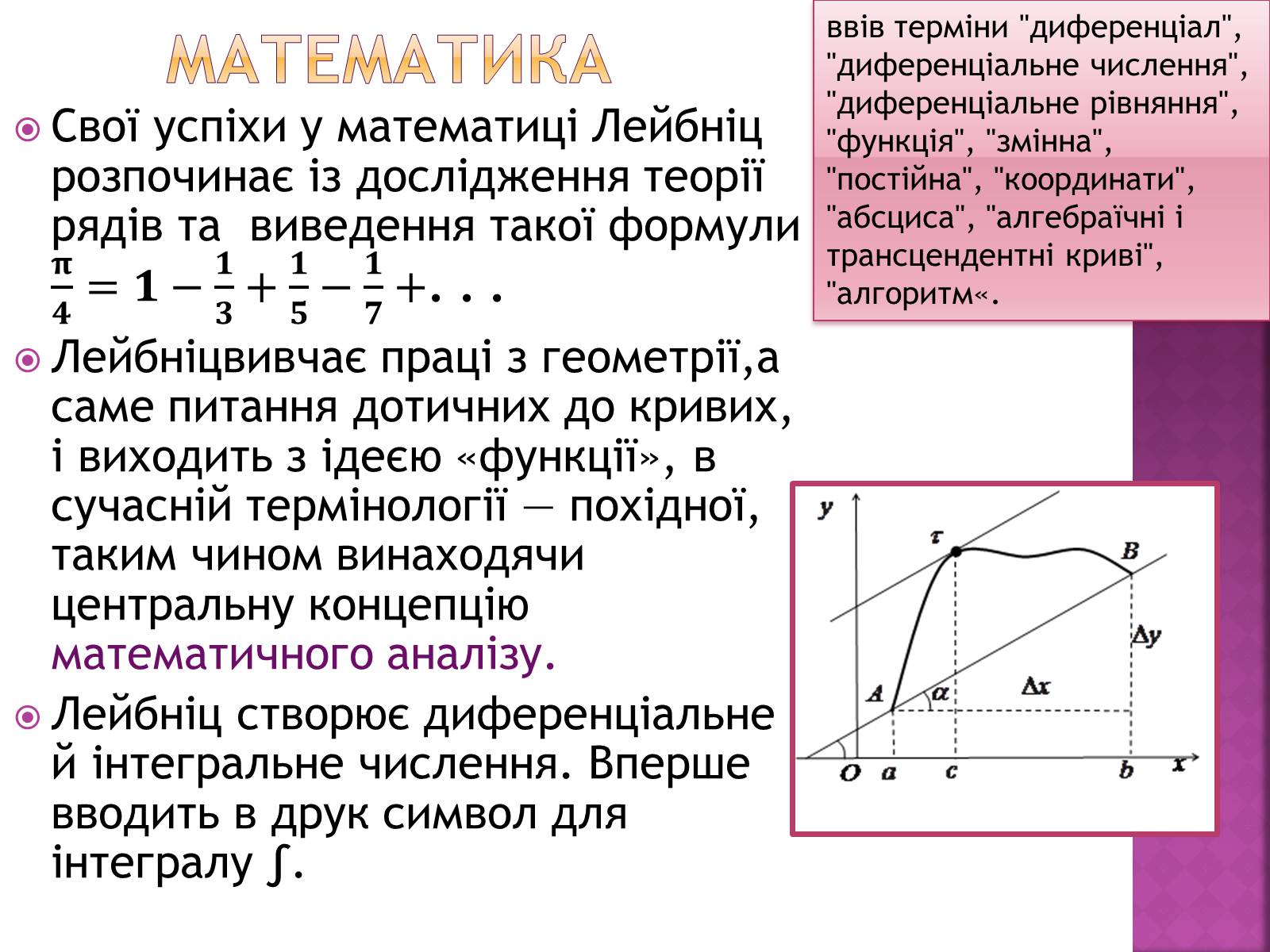
Лейбніцвивчає праці з геометрії,а саме питання дотичних до кривих, і виходить з ідеєю «функції», в сучасній термінології — похідної, таким чином винаходячи центральну концепцію математичного аналізу.
Лейбніц створює диференціальне й інтегральне числення. Вперше вводить в друк символ для інтегралу ∫.
ввів терміни "диференціал", "диференціальне числення", "диференціальне рівняння", "функція", "змінна", "постійна", "координати", "абсциса", "алгебраїчні і трансцендентні криві", "алгоритм«.
Свої успіхи у математиці Лейбніц розпочинає із дослідження теорії рядів та виведення такої формули . . .
Лейбніцвивчає праці з геометрії,а саме питання дотичних до кривих, і виходить з ідеєю «функції», в сучасній термінології — похідної, таким чином винаходячи центральну концепцію математичного аналізу.
Лейбніц створює диференціальне й інтегральне числення. Вперше вводить в друк символ для інтегралу ∫.
ввів терміни "диференціал", "диференціальне числення", "диференціальне рівняння", "функція", "змінна", "постійна", "координати", "абсциса", "алгебраїчні і трансцендентні криві", "алгоритм«.
Слайд #5
«Про приховану геометрію»
У своїх математичних працях учений виклав відповідні правила без доведень, відразу показуючи їх практичне застосування. У його праці, викладено правила інтегрування багатьох елементарних функцій, зокрема й тих, за допомогою яких швидко й легко виводилися формули обчислення площ, поверхонь і об'ємів-тіл обертання і тіл, обмежених кривими поверхнями взагалі.
Правила інтегрування
У своїх математичних працях учений виклав відповідні правила без доведень, відразу показуючи їх практичне застосування. У його праці, викладено правила інтегрування багатьох елементарних функцій, зокрема й тих, за допомогою яких швидко й легко виводилися формули обчислення площ, поверхонь і об'ємів-тіл обертання і тіл, обмежених кривими поверхнями взагалі.
Правила інтегрування

Слайд #6
Предок сьогоднішнього калькулятора
Лейбніц створив механічний калькулятор (арифмометр), що виконує додавання, віднімання, множення і ділення чисел, а також витяг коренів і зведення в степінь.
Лейбніц застосував систему числення, що використовує дві цифри: 0 і 1. Принцип двійкової системи числення Лейбніц пояснював на прикладі коробочки з отворами: відкритий отвір означає 1, закритий — 0. Одиниця позначалася кулею, що випала, нуль — відсутністю кулі. Двійкова система числення Лейбніца знайшла згодом застосування в автоматичних обчислювальних пристроях.
Лейбніц створив механічний калькулятор (арифмометр), що виконує додавання, віднімання, множення і ділення чисел, а також витяг коренів і зведення в степінь.
Лейбніц застосував систему числення, що використовує дві цифри: 0 і 1. Принцип двійкової системи числення Лейбніц пояснював на прикладі коробочки з отворами: відкритий отвір означає 1, закритий — 0. Одиниця позначалася кулею, що випала, нуль — відсутністю кулі. Двійкова система числення Лейбніца знайшла згодом застосування в автоматичних обчислювальних пристроях.

Слайд #7
Одне з найвизначніших досягнень
Лейбніц довів, що безкінечно малі величини можна ділити до безкінечності. Він стверджував що вони не мають початкової точки. Наприклад якщо ми ділитимемо 4 або 3, то наблизимося до результату ділення, але ніколи його не досягнемо, або якщо ділити 10 на 3 то одержимо 3. 33333333… Але конкретного вирішення ми так і незможемо побачити.Мабуть цю ситуацію варто розглядати як метафізичне явище, яке полягає в тому що кожний елемент в природі є цілісним і непереривним.
Лейбніц запропонував дію множення позначати однією крапкою, а ділення — двома,використовувати круглі, квадратні і фігурні дужки у формулах і різних перетвореннях.
Одна із праць Лейбніца
Лейбніц довів, що безкінечно малі величини можна ділити до безкінечності. Він стверджував що вони не мають початкової точки. Наприклад якщо ми ділитимемо 4 або 3, то наблизимося до результату ділення, але ніколи його не досягнемо, або якщо ділити 10 на 3 то одержимо 3. 33333333… Але конкретного вирішення ми так і незможемо побачити.Мабуть цю ситуацію варто розглядати як метафізичне явище, яке полягає в тому що кожний елемент в природі є цілісним і непереривним.
Лейбніц запропонував дію множення позначати однією крапкою, а ділення — двома,використовувати круглі, квадратні і фігурні дужки у формулах і різних перетвореннях.
Одна із праць Лейбніца

Слайд #8
Гармонія філософії та математики
В математиці Готфрід Лейбніц вбачав багато філософських ідей. Зокрема філософські суперечності пропонував вирішувати математичним шляхом. Він казав, що «у разі розходження поглядів між філософами, слід було взяти в руки пера, сісти за свої дошки і сказати один одному (по-дружньому) давайте порахуємо?»
В математиці Готфрід Лейбніц вбачав багато філософських ідей. Зокрема філософські суперечності пропонував вирішувати математичним шляхом. Він казав, що «у разі розходження поглядів між філософами, слід було взяти в руки пера, сісти за свої дошки і сказати один одному (по-дружньому) давайте порахуємо?»

Слайд #9
Філософія
Лейбніц став завершувачем філософії XVII століття і попередником німецької класичної філософії, його філософська система склалася до 1685 року як підсумок двадцятирічної еволюції, в процесі якої він критично переробив основні ідеї Демокріта, Платона, Августина, Декарта, Гоббса, Спінози та інших.
Загальновідома філософія Лейбніца викладена в «Монадології» і в «Началах природи і благодаті»; одну з названих робіт (невідомо яку) він написав для принца Євгенія Савойського, товариша по службі герцога Мальборо.
Лейбніц став завершувачем філософії XVII століття і попередником німецької класичної філософії, його філософська система склалася до 1685 року як підсумок двадцятирічної еволюції, в процесі якої він критично переробив основні ідеї Демокріта, Платона, Августина, Декарта, Гоббса, Спінози та інших.
Загальновідома філософія Лейбніца викладена в «Монадології» і в «Началах природи і благодаті»; одну з названих робіт (невідомо яку) він написав для принца Євгенія Савойського, товариша по службі герцога Мальборо.

Слайд #10
Є дві системи філософії, які представляють філософські погляди Лейбніца:
Одна, яку він відкрито проголошував, була оптимістичною, ортодоксальною, фантастичною і дрібною
Інша, яку поступово витягнули з його рукописів відносно недавні видавці, була глибокою, ясною, багато в чому схожою на філософію Спінози і дивно логічною.
Одна, яку він відкрито проголошував, була оптимістичною, ортодоксальною, фантастичною і дрібною
Інша, яку поступово витягнули з його рукописів відносно недавні видавці, була глибокою, ясною, багато в чому схожою на філософію Спінози і дивно логічною.

Слайд #11
Мона́да (від грец. μονάς — одиниця, неподільне) в ряді філософських систем — найпростіша, неподільна єдність, першопочаток, основа явищ. Учення про монади називають монадологією.
Лейбніц розвиває систему, що отримала назву «монадологія». Лейбніц першим системно і доказово представив розгляд Всесвіту як монади, тобто визнав монади індивідуальними складовими Всесвіту.
Лейбніц розвиває систему, що отримала назву «монадологія». Лейбніц першим системно і доказово представив розгляд Всесвіту як монади, тобто визнав монади індивідуальними складовими Всесвіту.

Слайд #12
Декарт допускав три субстанції: Бога, духа і матерію
Спіноза допускав одного Бога
Для Декарта протяжність є сутністю матерії
для Спінози і протяжність, і мислення є атрибутами Бога
Лейбніц вірив у нескінченне число субстанцій, які називав «монада». Кожна з них мала деякі властивості фізичної точки, але тільки коли її розглядали абстрактно, фактично ж кожна монада є душею.
Подібно до Декарта і Спінози, Лейбніц засновував свою філософію на понятті «субстанції», але він радикально відрізнявся від них у розгляді відносини духу і матерії й у розгляді числа субстанцій.
Спіноза допускав одного Бога
Для Декарта протяжність є сутністю матерії
для Спінози і протяжність, і мислення є атрибутами Бога
Лейбніц вірив у нескінченне число субстанцій, які називав «монада». Кожна з них мала деякі властивості фізичної точки, але тільки коли її розглядали абстрактно, фактично ж кожна монада є душею.
Подібно до Декарта і Спінози, Лейбніц засновував свою філософію на понятті «субстанції», але він радикально відрізнявся від них у розгляді відносини духу і матерії й у розгляді числа субстанцій.

Слайд #13
Вчення Лейбніца про монади:
Увесь світ складається з великої кількості субстанцій, які мають єдину природу
Принципово слід розрізняти світ розумовоосяжний (світ істинно сущого) і світ феноменальний (фізичний світ, який сприймається чуттям)
В основі світу лежать неподільні першоелементи – монади («духовні атоми»)
Усі вони об'єднані принципом попередньо встановленої гармонії
Монада володіє чотирма якостями: сприйняттям, уявленням, прагненням і потягом
Монади замкуті і незалежні один від одного
Існує чотири класи монади: «голі монади», «монади тварин», «монади людей», «Бог»
Увесь світ складається з великої кількості субстанцій, які мають єдину природу
Принципово слід розрізняти світ розумовоосяжний (світ істинно сущого) і світ феноменальний (фізичний світ, який сприймається чуттям)
В основі світу лежать неподільні першоелементи – монади («духовні атоми»)
Усі вони об'єднані принципом попередньо встановленої гармонії
Монада володіє чотирма якостями: сприйняттям, уявленням, прагненням і потягом
Монади замкуті і незалежні один від одного
Існує чотири класи монади: «голі монади», «монади тварин», «монади людей», «Бог»

Слайд #14
Висновок
Творчість Лейбніца мала величезне значення для розвитку світової науки. К. Маркс високо оцінював наукову спадщину вченого, а Ф. Енгельс говорив, що розум цієї талановитої людини, обдарованої творчою фантазією і прагненням до знань, ніби випромінював навколо себе найгеніальніші ідеї.
Творчість Лейбніца мала величезне значення для розвитку світової науки. К. Маркс високо оцінював наукову спадщину вченого, а Ф. Енгельс говорив, що розум цієї талановитої людини, обдарованої творчою фантазією і прагненням до знань, ніби випромінював навколо себе найгеніальніші ідеї.

Слайд #15
Використані джерела:
http://daviscountydaycare.com/storya-zaxdno-flosof/133-flosofya-novogo-chasu-lejbncz-.html
http://daviscountydaycare.com/kurs-lekczj-z-flosof/467-vchennya_pro_monada.html
http://subject.com.ua/philosophy/osnovi/46.html
http://uk.wikipedia.org/wiki/%D0%9C%D0%BE%D0%BD%D0%B0%D0%B4%D0%B0
http://www.ukrreferat.com/index.php?referat=30651
http://osvita.ua/vnz/reports/biograf/24015/
http://daviscountydaycare.com/storya-zaxdno-flosof/133-flosofya-novogo-chasu-lejbncz-.html
http://daviscountydaycare.com/kurs-lekczj-z-flosof/467-vchennya_pro_monada.html
http://subject.com.ua/philosophy/osnovi/46.html
http://uk.wikipedia.org/wiki/%D0%9C%D0%BE%D0%BD%D0%B0%D0%B4%D0%B0
http://www.ukrreferat.com/index.php?referat=30651
http://osvita.ua/vnz/reports/biograf/24015/
