Презентація на тему «Рішення комбінаторних задач»

Підготувала учениця 11 класу
Ананьєва Поліна
Рішення комбінаторних задач

Завдання, вирішуючи які доводиться складати різні комбінації з кінцевого числа елементів і підраховувати кількість комбінацій, отримали назву комбінаторних.
Розділ математики, в якому розглядають такі завдання, називають комбінаторикою.
Комбінаторика (від латинського combinare) означає "з'єднувати, поєднувати".
Загальна інформація

Почати перегляд задач

Державні прапори багатьох країн складаються з горизонтальних або вертикальних смуг різних кольорів. Скільки існує різних прапорів, що складаються з двох горизонтальних смуг однакової ширини і різного кольору - білого, червоного і синього?
Задача1
Для перегляду відповіді натисніть “Плей”

Нехай верхня смуга прапора - біла (Б). Тоді нижня смуга може бути червоною (Ч) або синьою (С). Отримали дві комбінації - два варіанти прапора.? Якщо верхня смуга прапора - червона, то нижня може бути білою або синьою. Отримаємо ще два варіанти прапора.? Нехай, нарешті, верхня смуга - синя, тоді нижня може бути білою або червоною. Це ще два варіанти прапора.? Всього отримали
3 • 2 = 6 комбінацій - шість варіантів прапорів.
рішення:
НАСТУПНА ЗАДАЧА

Скільки тризначних чисел можна скласти з цифр 1, 3, 5, 7?? Використовуючи в запису числа кожну з них не більше одного разу?
Задача 2
Для перегляду відповіді натисніть “Плей”

Щоб відповісти на це питання , випишемо всі такі числа. Нехай на першому місці стоїть цифра 1 . На другому місці може бути записана будь-яка з цифр 3 , 5 , 7 . Запишемо , наприклад , на другому місці цифру 3 . Тоді в якості третьої цифри можна взяти 5 або 7 . Отримаємо два числа 135 і 137 . Якщо на другому місці записати цифру 5 , то в якості третьої цифри можна взяти цифру 3 чи 7 . У цьому випадку отримаємо числа 153 і 157 . Якщо ж , нарешті , на другому місці записати цифру 7 , то отримаємо числа 173 і 175 . ? Отже , ми склали всі числа , які починаються з цифри 1 . ? Таких чисел шість: 135 , 137 , 153 , 157 , 173 , 175 . Аналогічним способом можна скласти числа , які починаються з цифри 2 , з цифри 5 , з цифри 7 .
Отримані результати запишемо в чотири рядки , в кожній з яких шість чисел :
135 , 137 , 153 , 157 , 173 , 175 ,
315 , 317 , 351 , 357 , 371 , 375 ,
513 , 517 , 531 , 537 , 571 , 573 ,
713 , 715 , 731 , 735 , 751 , 753 ,
Таким чином , з цифр 1 , 3 , 5 , 7 (без повторення цифр) можна скласти 24 тризначних числа.
рішення:
НАСТУПНА ЗАДАЧА

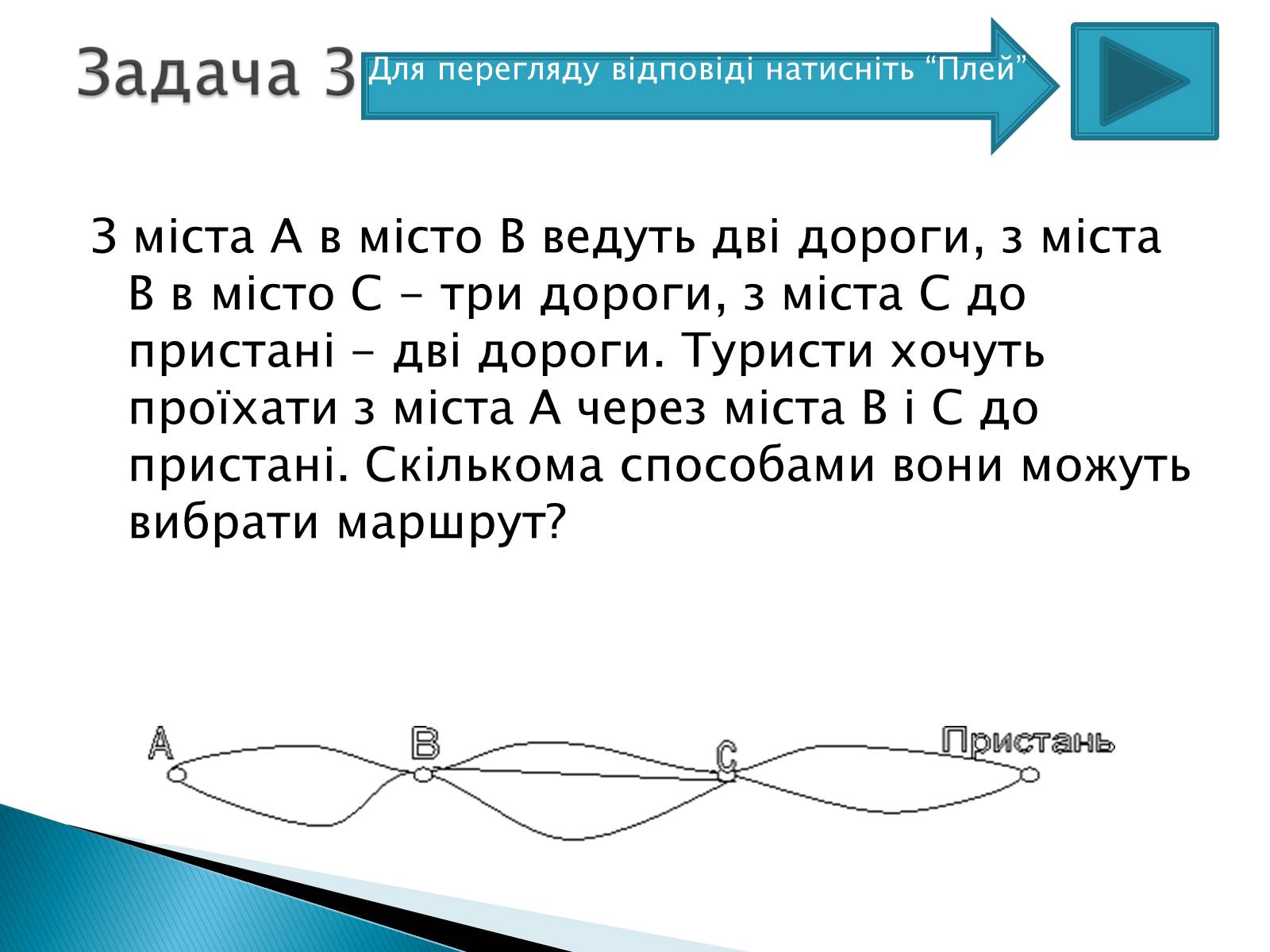
З міста А в місто В ведуть дві дороги, з міста В в місто С - три дороги, з міста С до пристані - дві дороги. Туристи хочуть проїхати з міста А через міста В і С до пристані. Скількома способами вони можуть вибрати маршрут?
Задача 3
Для перегляду відповіді натисніть “Плей”

Шлях з А в В туристи можуть вибрати двома способами. Далі в кожному випадку вони можуть проїхати з В в З трьома способами. Значить, є 2 • 3 варіантів маршруту з А в С. Так як з міста С на пристань можна потрапити двома способами, то всього існує 2 • 3 • 2, тобто 12 способів вибору туристами маршруту з міста А до пристані.
рішення:
НАСТУПНА ЗАДАЧА

Скільки існує прапорів складених з трьох горизонтальних смуг однакової ширини і різних кольорів-білого, зеленого, червоного і синього?
Задача 4
Для перегляду відповіді натисніть “Плей”

Таким чином, 4 • 3 • 2 = 24 прапора.
рішення:
НАСТУПНА ЗАДАЧА

Скільки різних тризначних чисел (без повторення цифр) можна скласти з непарних чисел, які є кратними 5.? Перш ніж вирішувати це завдання, давайте повторимо, які цифри непарні? Які числа є кратними 5.
Задача 5
Для перегляду відповіді натисніть “Плей”

Непарні цифри: 1, 3, 5, 7, 9.? У даному випадку, щоб число було кратним 5, воно повинно закінчуватися на 5.
Таким чином, 4 • 3 • 1 = 12 чисел.
рішення::
НАСТУПНА ЗАДАЧА

У шкільній їдальні пропонують 2 перших страви: борщ, локшина - і 4 других страви: пельмені, котлети, гуляш, риба. Скільки обідів з двох страв може замовити відвідувач.? Перерахуйте їх.
Задача 6
Для перегляду відповіді натисніть “Плей”

1 страва: Б Л 2 можливі 2 страви: П К Г Р П К Г Р
по 4. Таким чином, 2 • 4 = 8 різних обідів:
Борщ, пельмені; Локшина, пельмені;
Борщ, котлети; Локшина, котлети ;
Борщ, гуляш; Локшина, гуляш;
Борщ, риба; Локшина, риба.
рішення:
НАСТУПНА ЗАДАЧА

Учні 6 класу вирішили обмінятися фотографіями. Скільки фотографій для цього буде потрібно, якщо в класі 11 учнів.
Задача 7
Для перегляду відповіді натисніть “Плей”

11 чоловік по 10 фотографій.
11 • 10 = 110 (фотографій).
рішення:
НАСТУПНА ЗАДАЧА

З села Тернівка в село Родничок ведуть три дороги, а з села Родничок в місто Балашов - чотири дороги. Скількома способами можна потрапити з села Тернівка в місто Балашов через село Родничок?
Задача 8
Для перегляду відповіді натисніть “Плей”

3 дороги по 4 варіанти, тобто
3 • 4 = 12 (способів).
рішення:
НАСТУПНА ЗАДАЧА

У кафе є чотири перших страви, п'ять других та два третіх. Скількома способами відвідувачі кафе можуть вибрати обід, що складається з першого, другого і третього страв?
Задача 9
Для перегляду відповіді натисніть “Плей”

4 • 5 • 2 = 40 (способів)
рішення:
ЗАВЕРШИТИ ПЕРЕГЛЯД