Презентація на тему «Теорема Пифагора» (варіант 2)

Теорема Пифагора
Прямоугольный треугольник

Прежде чем говорить о теореме Пифагора я хочу немного рассказать о её авторе. О великом математике и философе, который сыграл большую роль в развитии математики и является известным представителем эллинской культуры.
Точных исторических данных о жизни и деятельности Пифагора не сохранилось. Ведомости про него находим только в отдельных высказываниях, воспоминаниях и комментариях к научным работам авторов позднего времени.

По рассказам, Пифагор родился приблизительно 580 лет до н. э. на о.Самос у ионийского побережья Средиземного моря, в богатой купеческой семье. Первые научные знания он получил от учёного Фэрэкида с города Сироса. Был знаком с уже известным на то время философом-математиком Фалесом и по его совету отправился в Египет, который тогда был центром научной и исследовательской деятельности. Прожив в Египте 22 года и в Вавилоне 12 лет, он приобрёл глубокие знания по природным и математическим наукам.

Позже в городе Кротоне он собрал вокруг себя группу единомышленников, главным образом аристократов, и создал тайный кружок. Все участники кружка и сам Пифагор подверглись гонениям. Они были вынуждены бежать из Кротона в Метапонт, где в одной из ночных уличных столкновений оборвалась жизнь 80-летнего ученого.
Пифагорийцы уделяли большое внимание исследовательской деятельности в сфере алгебре и геометрии.

Большое внимание Пифагорийцы уделяли исследованию особенностей прямоугольного треугольника, стороны которого определяются елыми числами. Можем предположить, что самый простой из таких треугольников, так называемый египетский треугольник со сторонами 3, 4, 5, был известен Пифагору еще во время его пребывания в Египте.

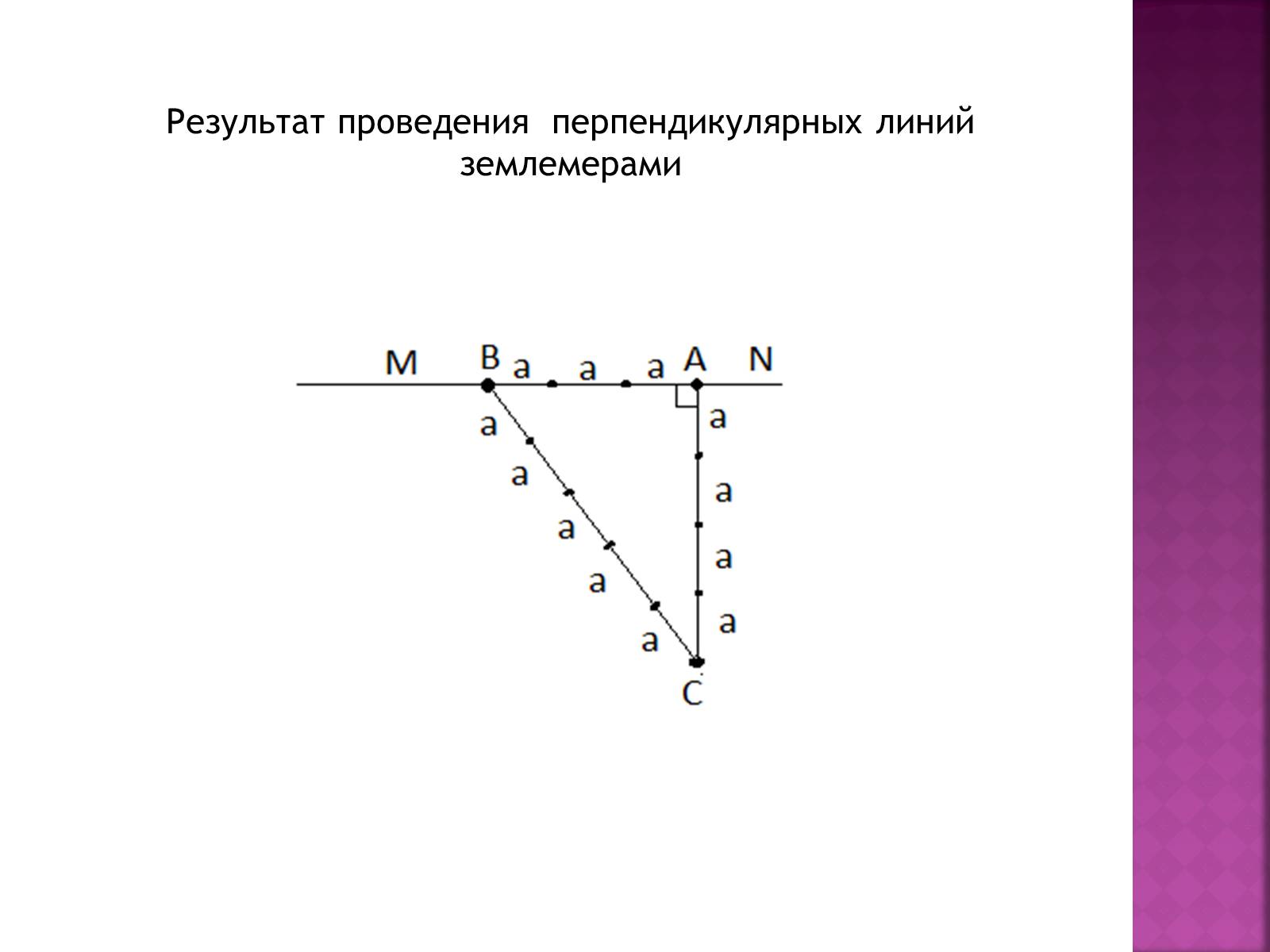
Тысячелетия назад строителями египетских пирамид использовался древний способ, который основывается на том, что каждый треугольник, стороны которого относятся как 3:4:5, соответственно общеизвестной теоремы Пифагора, - прямоугольный, так как
32 + 42 =52.
Удобный и очень точный способ, который используют землемеры для проведения на местности перпендикулярных линий, состоит в следующем. Пусть через точку А нужно к прямой MN провести перпендикуляр. От точки А откладывают в направлении АM три раза некоторое расстояние а. потом завязывают на шнуре три узла, расстояние между которыми равны 4а и 5а. Приложив крайние узлы к точкам А и В, натягивают шнур за средний узел. Шнур размещается треугольником, у которого угол А – прямой.
M

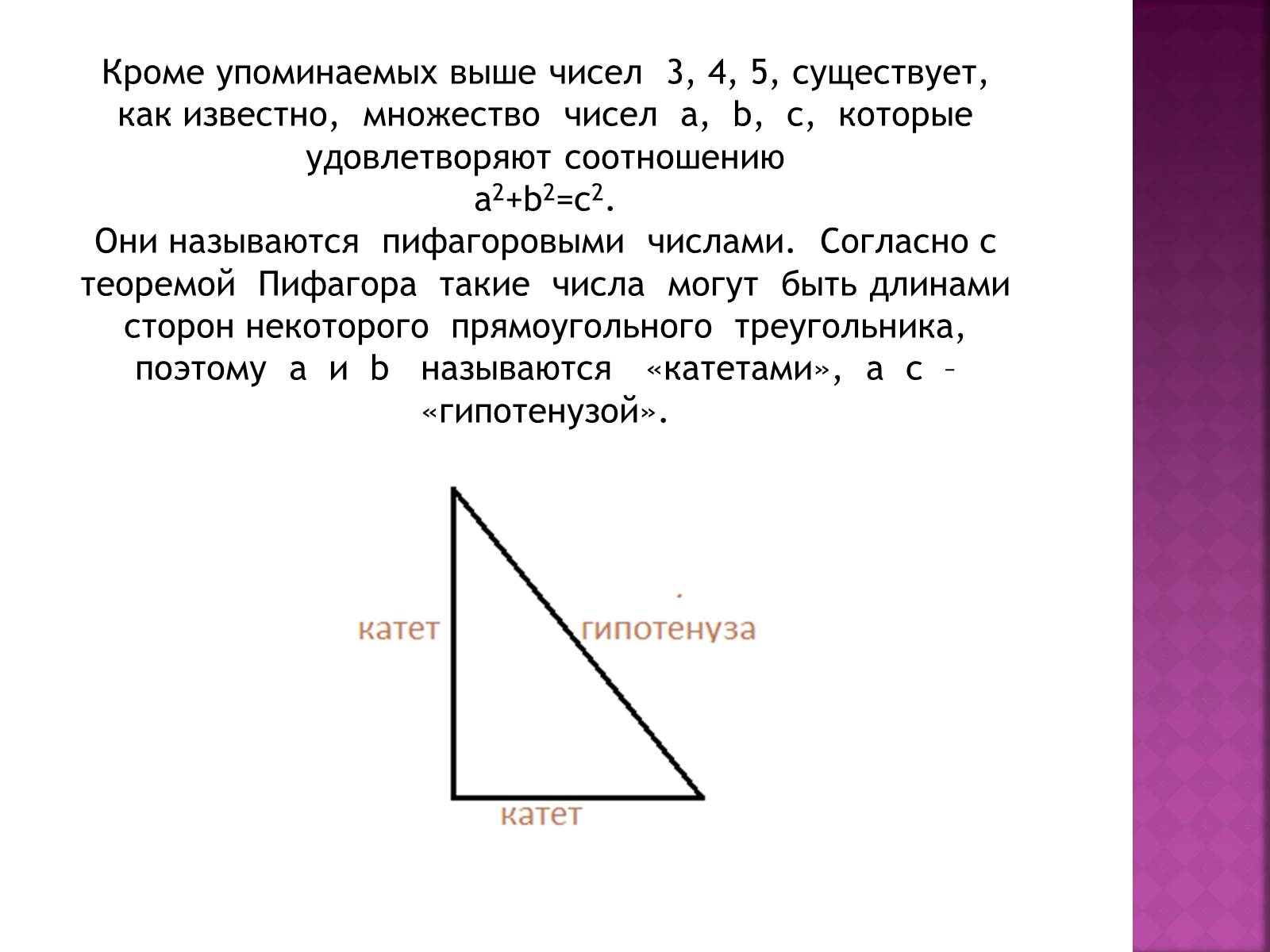
Кроме упоминаемых выше чисел 3, 4, 5, существует, как известно, множество чисел a, b, c, которые удовлетворяют соотношению
a2+b2=c2.
Они называются пифагоровыми числами. Согласно с теоремой Пифагора такие числа могут быть длинами сторон некоторого прямоугольного треугольника, поэтому a и b называются «катетами», а c – «гипотенузой».

Результат проведения перпендикулярных линий землемерами

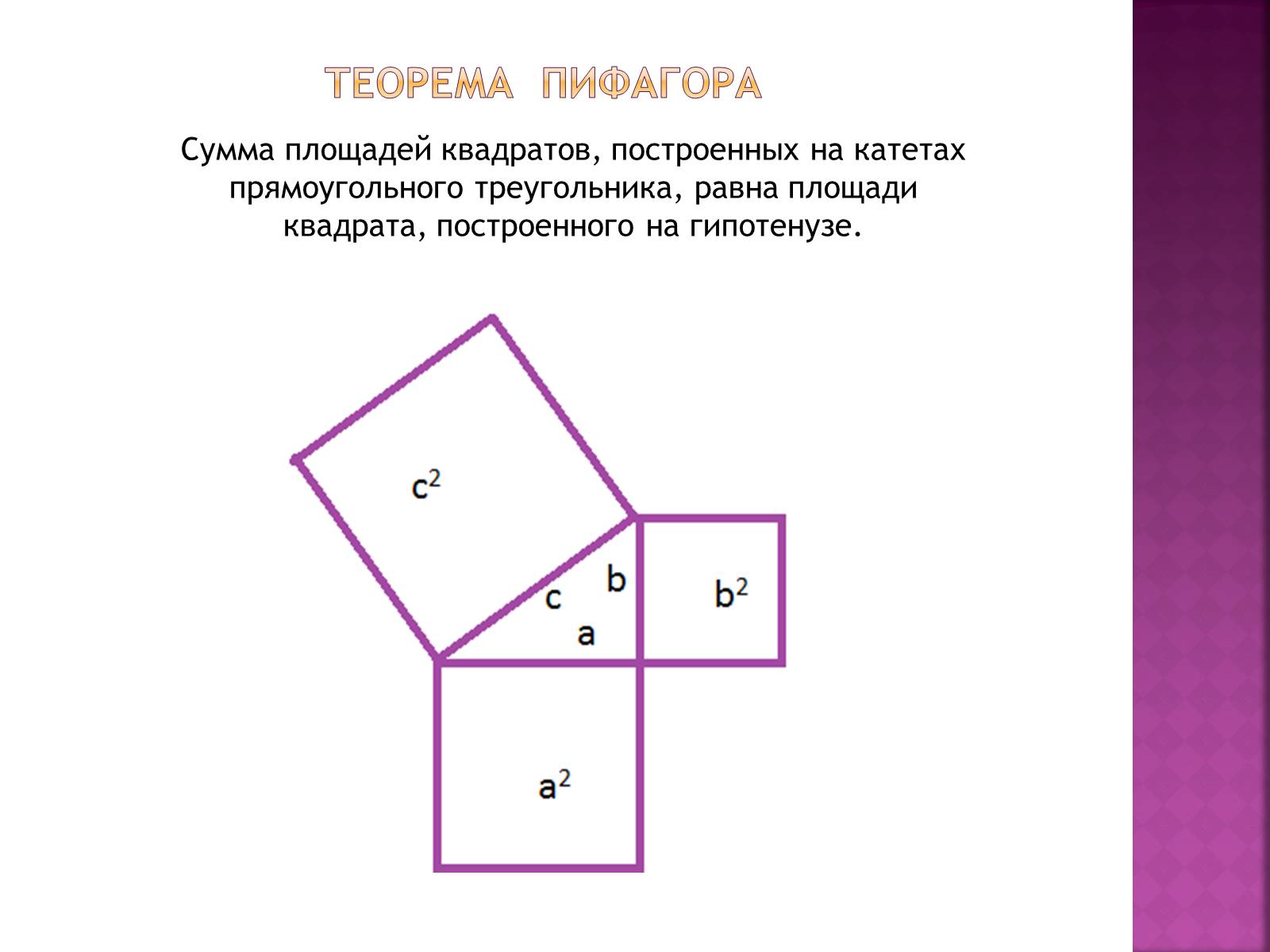
Теорема пифагора
Сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе.

Здесь не помогут ямб и дольник,хорей и дактиль грудь не выставят.Попав в любовный треугольник,готовься выдюжить и выстоять,на плечи взять хрустальным грузомсознанье: разобьешься вдребезги! -И по его гипотенузепройти, страховкою побрезговав;измерить все своим аршином,и торопясь - ведь все мы смертные! -его углы, его вершиныпостичь без всякой геометрии:лбом - об углы! Вершины - приступомсердечным, нитроглицериновым (уж если кудри серебристые,не дорожить же сердцевиною!)Ни теореме Пифагоране поддается он, ни времени -Любви Бермудский Треугольникразносторонний, тазобедренный...
Треугольник