- Головна
- Готові шкільні презентації
- Презентація на тему «Абстрактное моделирование прикладных задач»
Презентація на тему «Абстрактное моделирование прикладных задач»
225
Слайд #1
Министерство образования и науки Украины
Запорожское териториальное отделение
Малой академии наук Украини
Профиль - физико-математический
Секция - математика
Абстрактное моделирование
прикладных задач
Научная работа
Ученика 8 – А класса
Коммунального заведения
Днепрорудненская Гимназия «София»
Васильевского районного совета
Запорожской области
Шевченко Павла Юрьевича
Научный руководитель
Учитель математики
Патрушева Маргарита Полиевктовна
Запорожское териториальное отделение
Малой академии наук Украини
Профиль - физико-математический
Секция - математика
Абстрактное моделирование
прикладных задач
Научная работа
Ученика 8 – А класса
Коммунального заведения
Днепрорудненская Гимназия «София»
Васильевского районного совета
Запорожской области
Шевченко Павла Юрьевича
Научный руководитель
Учитель математики
Патрушева Маргарита Полиевктовна

Слайд #2
Содержание
Вступление
Раздел 1 –
3. Раздел 2 - Применение моделирование при решении задач на движение
4. Раздел 3 - Сравнительный анализ решений задачи на движение
3.1. Решение уравнением
3.2. Решение системой
3.3. Решение графически
5. Раздел 4 - Модели в виде «Графов»
6. Выводы
7. Литература
Применение моделирование при решении задач по экономике
Вступление
Раздел 1 –
3. Раздел 2 - Применение моделирование при решении задач на движение
4. Раздел 3 - Сравнительный анализ решений задачи на движение
3.1. Решение уравнением
3.2. Решение системой
3.3. Решение графически
5. Раздел 4 - Модели в виде «Графов»
6. Выводы
7. Литература
Применение моделирование при решении задач по экономике

Слайд #3
Вступление
Математическими методами решают не только абстрактные математические задачи о числах, фигурах, уравнениях, функциях и т. д., но и многие прикладные задачи. Прикладными задачами в математике называют задачи, условия которых содержат нематематические понятия. Решая прикладную задачу математическими методами, сначала создают её математическую модель.
Моделью называют специально созданный объект, отображающий свойства исследуемого предмета.
Например уменьшенные модели самолета, плотины, автомобиля – это примеры физических моделей. Математические модели создают, используя математические понятия и отношения: геометрические фигуры, числа, выражения и т. п. В большинстве случаев математическими объектами бывают функции, уравнения, неравенства и их системы.
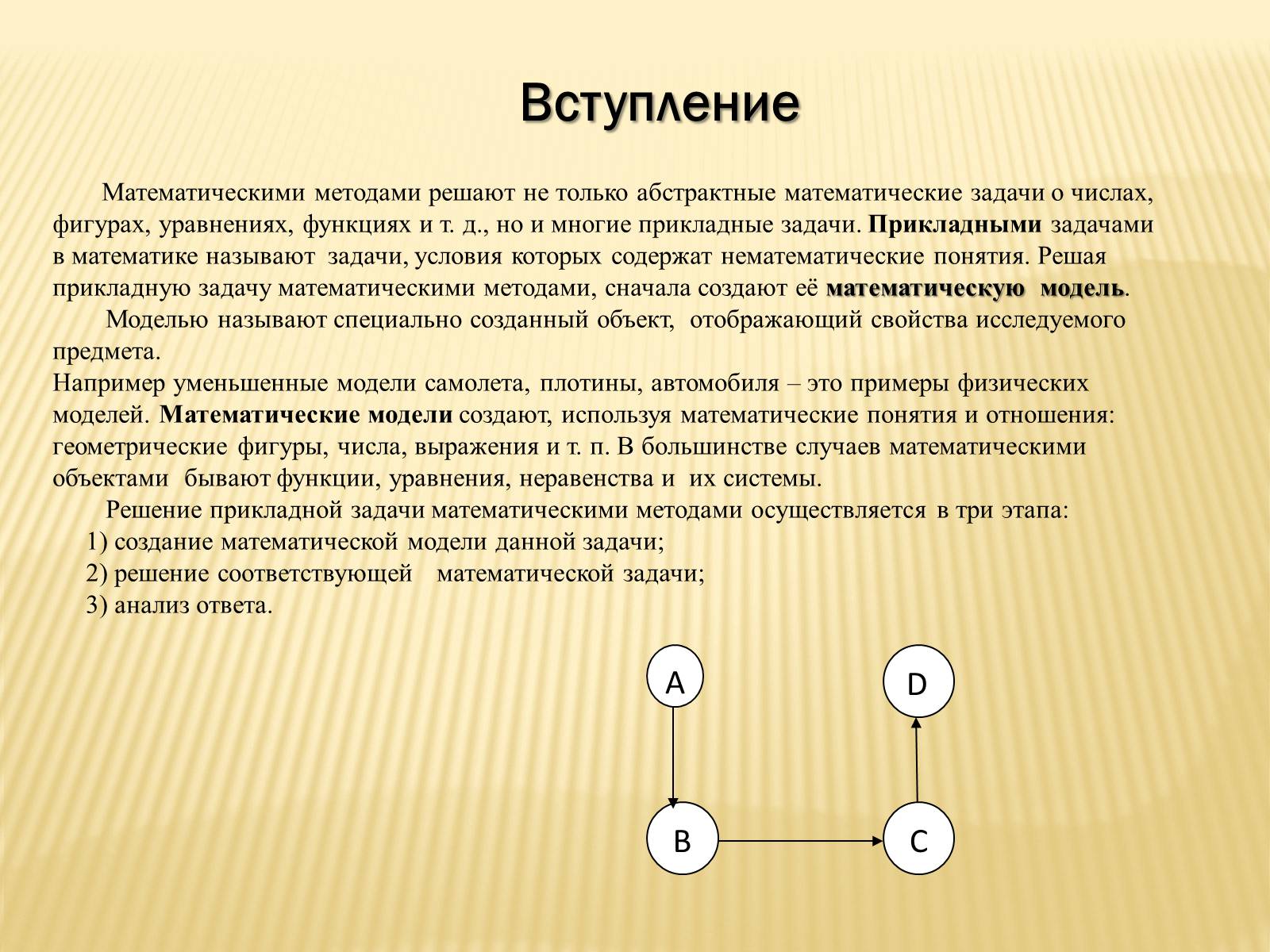
Решение прикладной задачи математическими методами осуществляется в три этапа:
1) создание математической модели данной задачи;
2) решение соответствующей математической задачи;
3) анализ ответа.
А
B
C
D
Математическими методами решают не только абстрактные математические задачи о числах, фигурах, уравнениях, функциях и т. д., но и многие прикладные задачи. Прикладными задачами в математике называют задачи, условия которых содержат нематематические понятия. Решая прикладную задачу математическими методами, сначала создают её математическую модель.
Моделью называют специально созданный объект, отображающий свойства исследуемого предмета.
Например уменьшенные модели самолета, плотины, автомобиля – это примеры физических моделей. Математические модели создают, используя математические понятия и отношения: геометрические фигуры, числа, выражения и т. п. В большинстве случаев математическими объектами бывают функции, уравнения, неравенства и их системы.
Решение прикладной задачи математическими методами осуществляется в три этапа:
1) создание математической модели данной задачи;
2) решение соответствующей математической задачи;
3) анализ ответа.
А
B
C
D
Слайд #4
Раздел 1 –Применение моделирование при решении задач по экономике
Задача 1
Затраты на перевозку груза двумя видами
транспорта вычисляются по формулам:
Где х – расстояние перевозок в сотнях километров,
– транспортные затраты при перевозке груза первым и вторым
видами транспорта в сотнях гривен. Определить, на какие расстояния
и каким транспортом лучше всего перевозить груз.
Аналитическое решение
Задача 1
Затраты на перевозку груза двумя видами
транспорта вычисляются по формулам:
Где х – расстояние перевозок в сотнях километров,
– транспортные затраты при перевозке груза первым и вторым
видами транспорта в сотнях гривен. Определить, на какие расстояния
и каким транспортом лучше всего перевозить груз.
Аналитическое решение

Слайд #5
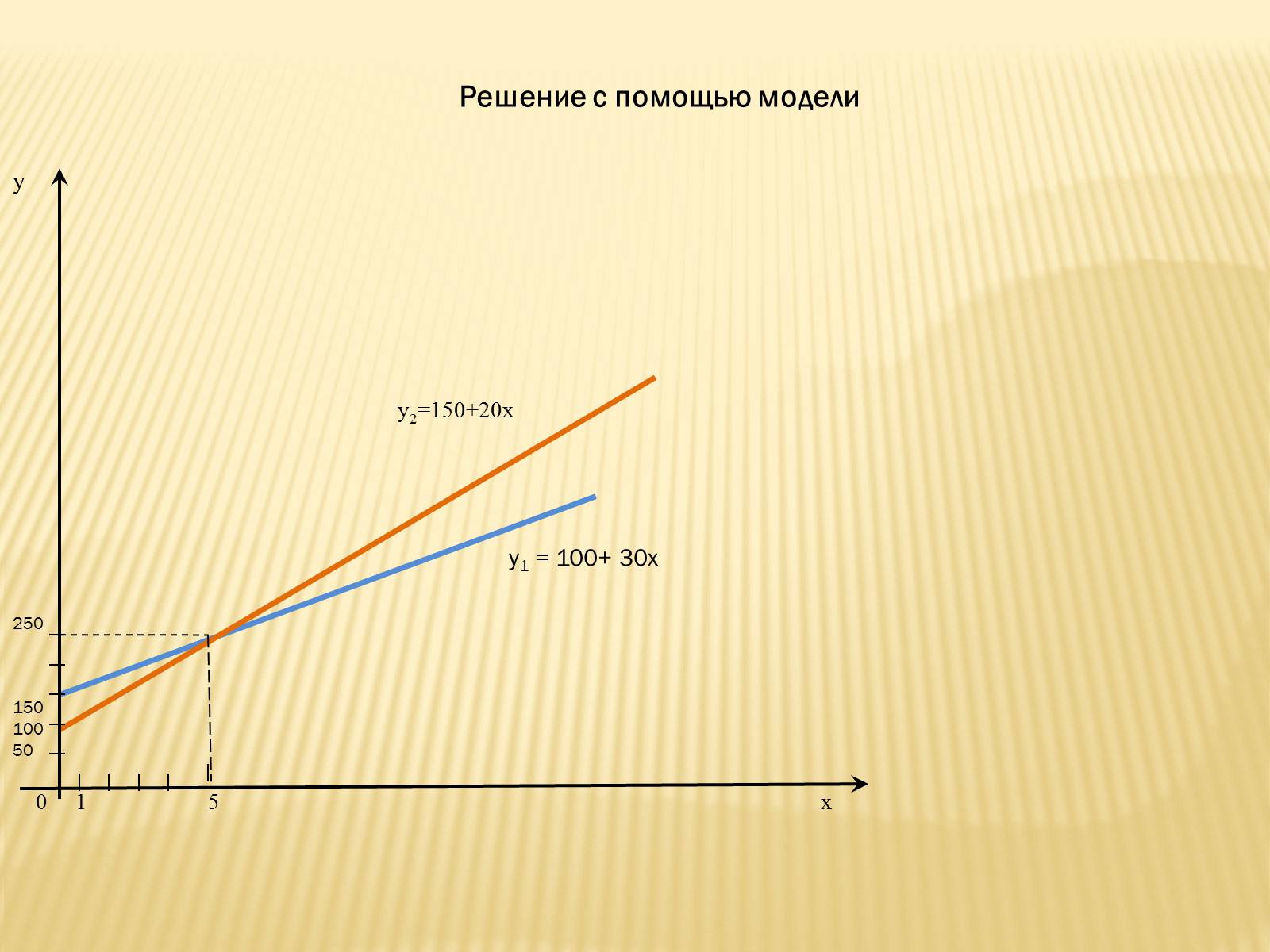
Решение с помощью модели
y
250
150
100
50
y2=150+20x
y1 = 100+ 30x
0 1 5 x
y
250
150
100
50
y2=150+20x
y1 = 100+ 30x
0 1 5 x
Слайд #6
Задача 2
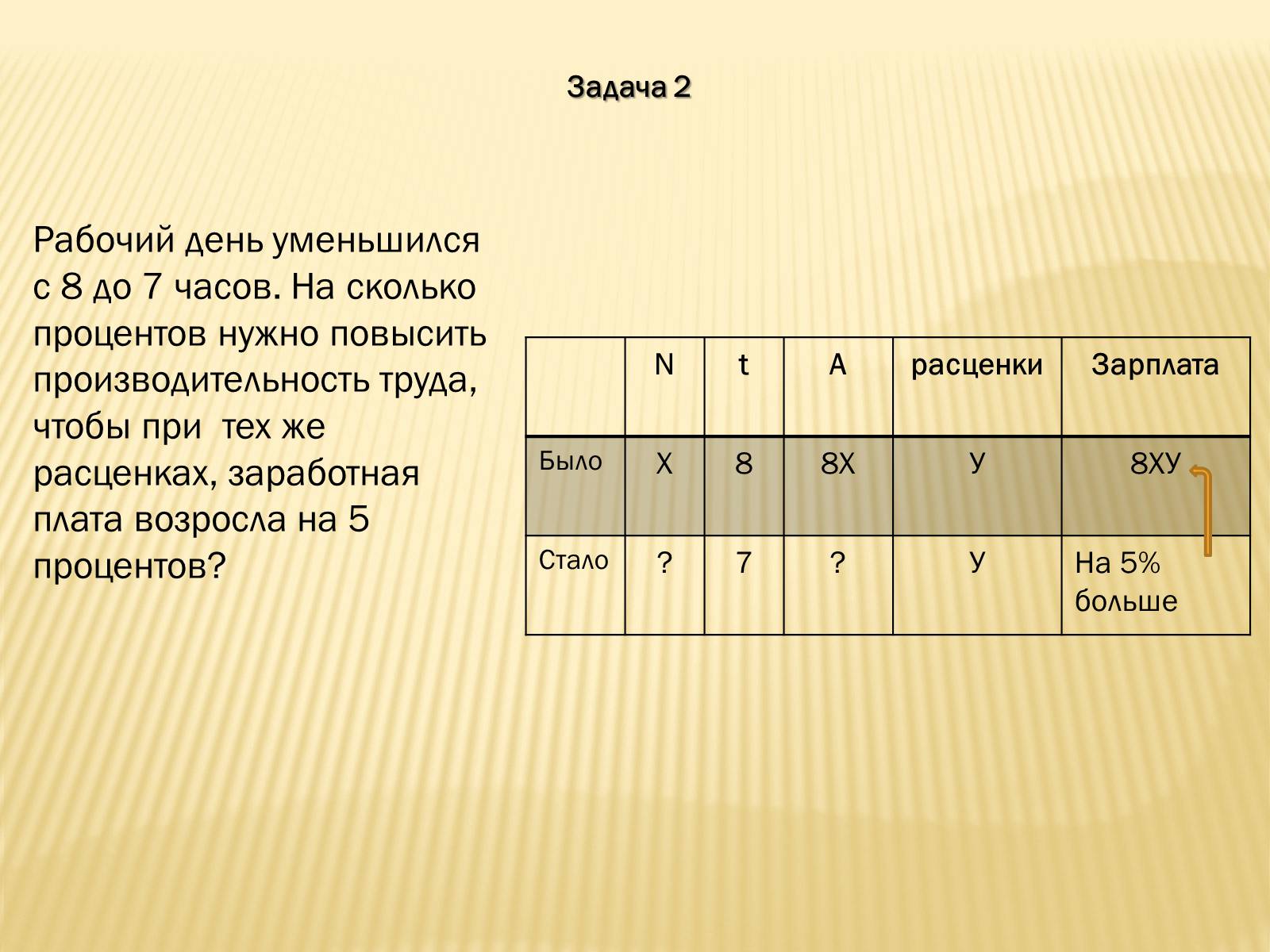
N
t
A
расценки
Зарплата
Было
Х
8
8Х
У
8ХУ
Стало
?
7
?
У
На 5% больше
Рабочий день уменьшился с 8 до 7 часов. На сколько процентов нужно повысить производительность труда, чтобы при тех же расценках, заработная плата возросла на 5 процентов?
N
t
A
расценки
Зарплата
Было
Х
8
8Х
У
8ХУ
Стало
?
7
?
У
На 5% больше
Рабочий день уменьшился с 8 до 7 часов. На сколько процентов нужно повысить производительность труда, чтобы при тех же расценках, заработная плата возросла на 5 процентов?
Слайд #7
Задача 3
Предприятие выпускает изделия двух типов. Обработка каждого изделия первого типа занимает 5 часов в цехе А и 3 часа в цехе В. обработка каждого изделия второго типа занимает 2 часа в цехе А и 4 ч в цехе В. Цех А может работать не более 150 ч в месяц, а цех В – не более 132 ч в месяц. Из каждого изделия первого и второго типов производство получает прибыль в 300 и 200 грн соответственно. Определить, сколько изделий каждого типа следует производить ежемесячно, чтобы обеспечить производству наибольшую прибыль. Найти эту прибыль.
Предприятие выпускает изделия двух типов. Обработка каждого изделия первого типа занимает 5 часов в цехе А и 3 часа в цехе В. обработка каждого изделия второго типа занимает 2 часа в цехе А и 4 ч в цехе В. Цех А может работать не более 150 ч в месяц, а цех В – не более 132 ч в месяц. Из каждого изделия первого и второго типов производство получает прибыль в 300 и 200 грн соответственно. Определить, сколько изделий каждого типа следует производить ежемесячно, чтобы обеспечить производству наибольшую прибыль. Найти эту прибыль.

Слайд #8
Решение
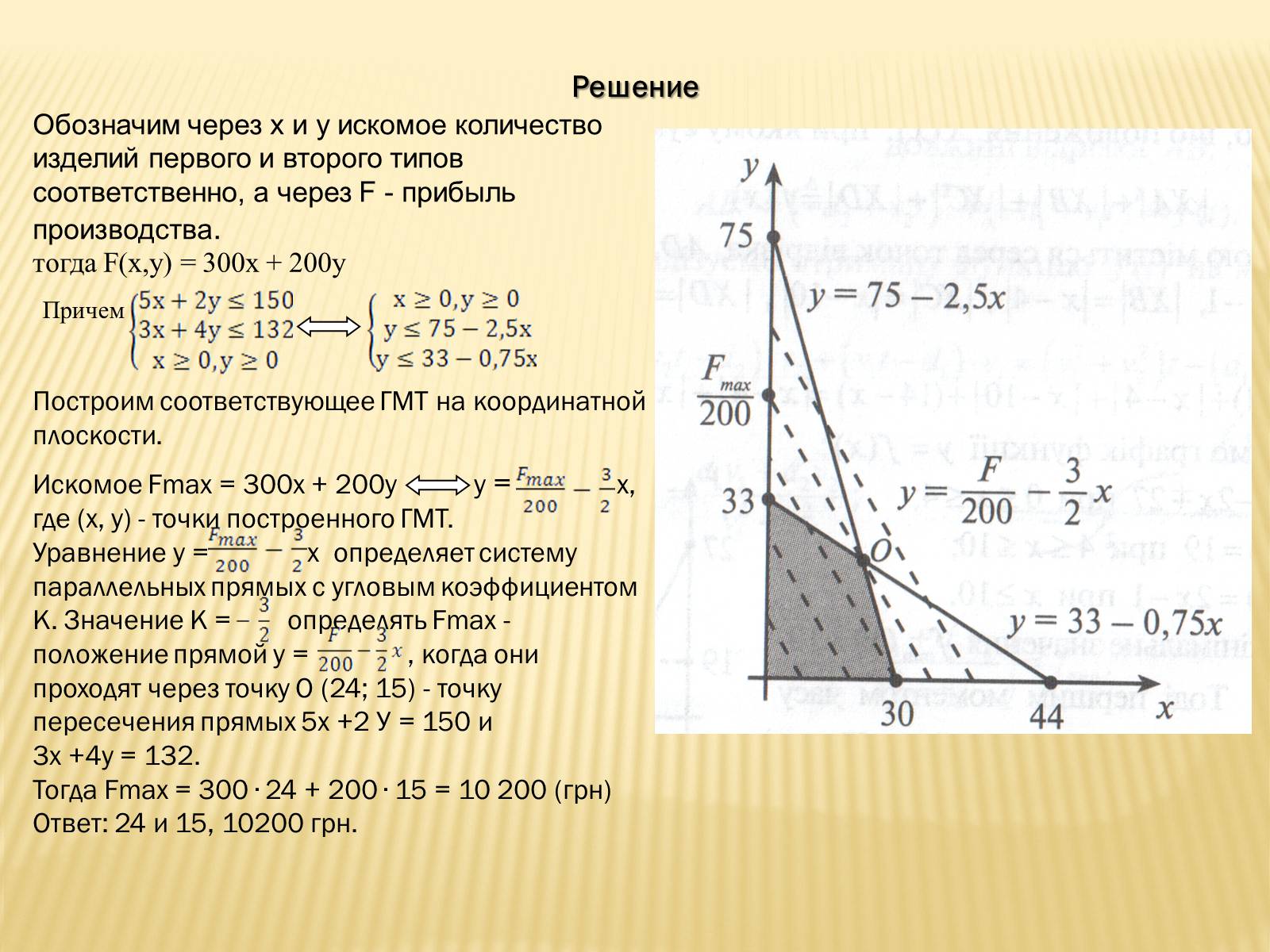
Обозначим через х и у искомое количество изделий первого и второго типов соответственно, а через F - прибыль производства.
тогда F(x,y) = 300х + 200у
Причем
Построим соответствующее ГМТ на координатной плоскости.
Искомое Fmах = 300х + 200у у = х, где (х, у) - точки построенного ГМТ.Уравнение у = х определяет систему параллельных прямых с угловым коэффициентом K. Значение К = определять Fmaх - положение прямой у = , когда они
проходят через точку О (24; 15) - точку пересечения прямых 5х +2 У = 150 и
3х +4у = 132.Тогда Fmах = 300 ∙ 24 + 200 ∙ 15 = 10 200 (грн)Ответ: 24 и 15, 10200 грн.
Обозначим через х и у искомое количество изделий первого и второго типов соответственно, а через F - прибыль производства.
тогда F(x,y) = 300х + 200у
Причем
Построим соответствующее ГМТ на координатной плоскости.
Искомое Fmах = 300х + 200у у = х, где (х, у) - точки построенного ГМТ.Уравнение у = х определяет систему параллельных прямых с угловым коэффициентом K. Значение К = определять Fmaх - положение прямой у = , когда они
проходят через точку О (24; 15) - точку пересечения прямых 5х +2 У = 150 и
3х +4у = 132.Тогда Fmах = 300 ∙ 24 + 200 ∙ 15 = 10 200 (грн)Ответ: 24 и 15, 10200 грн.
Слайд #9
Раздел 2 - Применение моделирование при решении задач на движение
Задача1
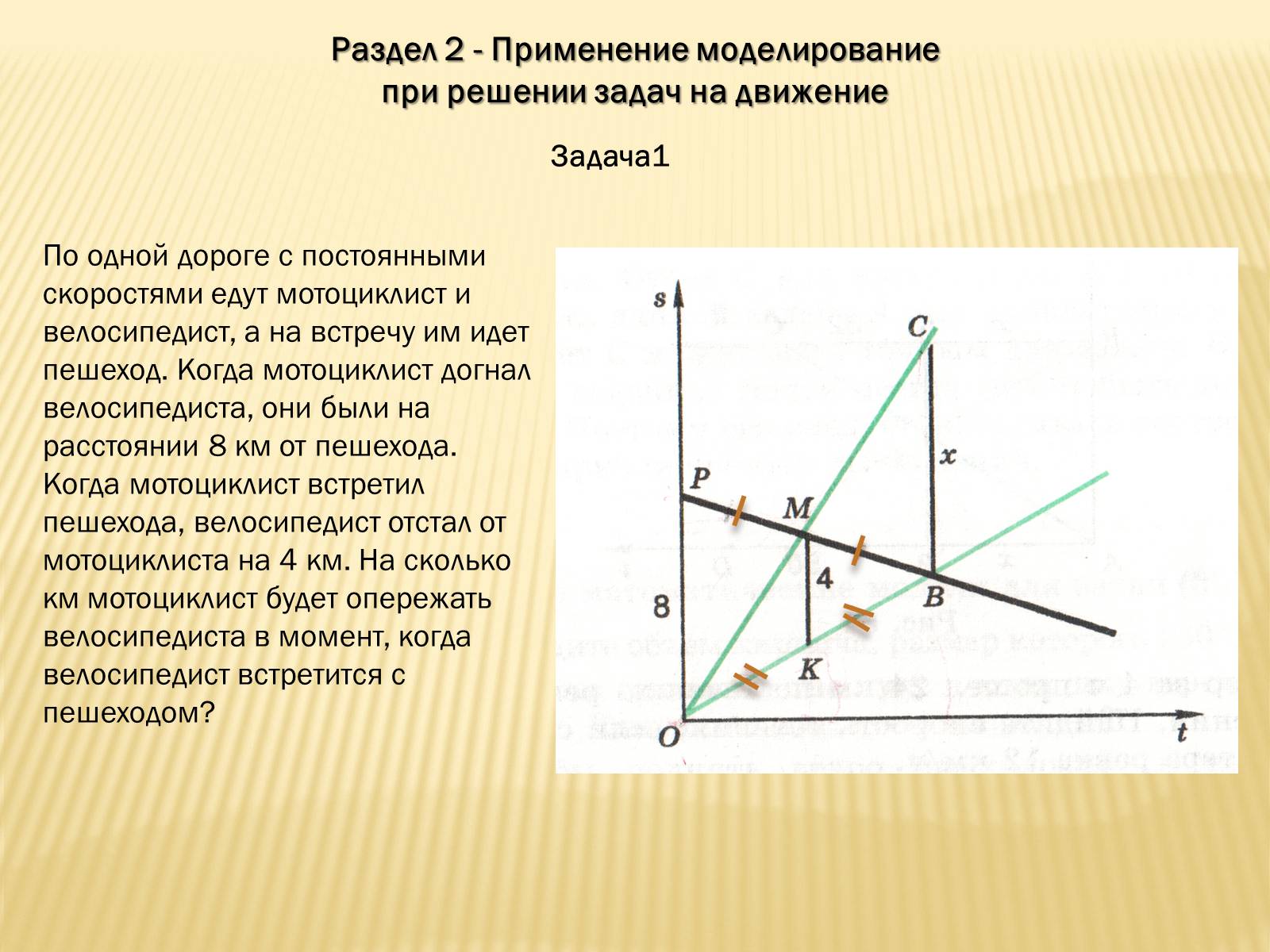
По одной дороге с постоянными скоростями едут мотоциклист и велосипедист, а на встречу им идет пешеход. Когда мотоциклист догнал велосипедиста, они были на расстоянии 8 км от пешехода. Когда мотоциклист встретил пешехода, велосипедист отстал от мотоциклиста на 4 км. На сколько км мотоциклист будет опережать велосипедиста в момент, когда велосипедист встретится с пешеходом?
Задача1
По одной дороге с постоянными скоростями едут мотоциклист и велосипедист, а на встречу им идет пешеход. Когда мотоциклист догнал велосипедиста, они были на расстоянии 8 км от пешехода. Когда мотоциклист встретил пешехода, велосипедист отстал от мотоциклиста на 4 км. На сколько км мотоциклист будет опережать велосипедиста в момент, когда велосипедист встретится с пешеходом?
Слайд #10
Задача 2
Вдоль прямолинейной дороги последовательно размещены населенные пункты А, В, С, D. Причем АВ = 3км, ВС = 6км, СD = 4км. На этой дороге слева от этих населенных пунктов на расстоянии 1км от А находится турист, который начинает двигаться к D со скоростью 3км / ч. Найти первый момент времени, когда сумма расстояний от туриста с пунктами А, В, С, D будет минимальной.
Вдоль прямолинейной дороги последовательно размещены населенные пункты А, В, С, D. Причем АВ = 3км, ВС = 6км, СD = 4км. На этой дороге слева от этих населенных пунктов на расстоянии 1км от А находится турист, который начинает двигаться к D со скоростью 3км / ч. Найти первый момент времени, когда сумма расстояний от туриста с пунктами А, В, С, D будет минимальной.

Слайд #11
Решение
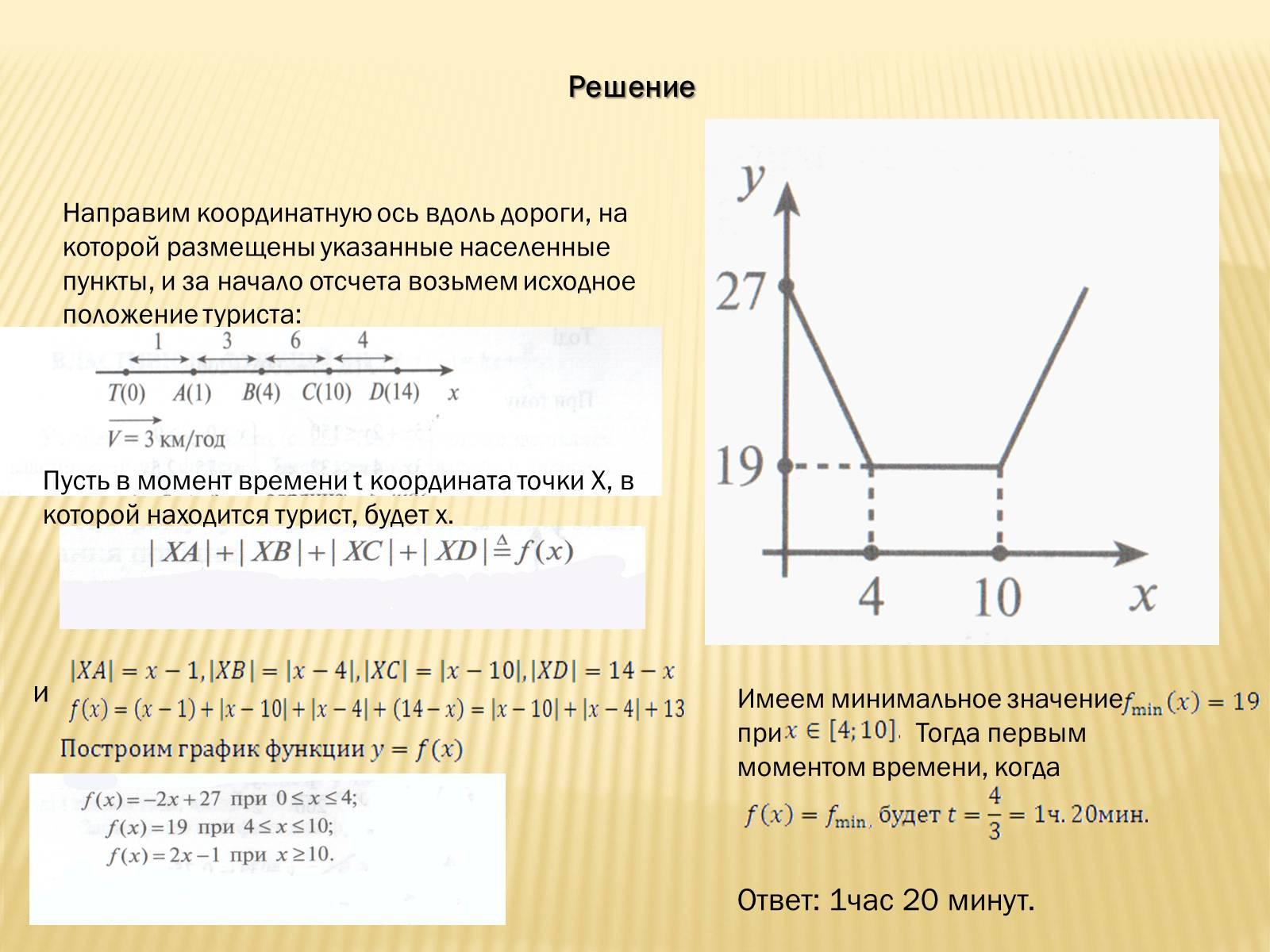
Направим координатную ось вдоль дороги, на которой размещены указанные населенные пункты, и за начало отсчета возьмем исходное положение туриста:
Пусть в момент времени t координата точки X, в которой находится турист, будет х.
и
Имеем минимальное значение
при Тогда первым моментом времени, когда
Ответ: 1час 20 минут.
Направим координатную ось вдоль дороги, на которой размещены указанные населенные пункты, и за начало отсчета возьмем исходное положение туриста:
Пусть в момент времени t координата точки X, в которой находится турист, будет х.
и
Имеем минимальное значение
при Тогда первым моментом времени, когда
Ответ: 1час 20 минут.
Слайд #12
Раздел 3 – Сравнительный анализ решений задачи на движение
Два парома одновременно отплывают от противоположных берегов реки и пересекают ее перпендикулярно берегам. Скорости паромов постоянные, но разные. Паромы встречаются на расстоянии 720 метров от одного из берегов, после чего продолжают движение. Достигнув берегов, паромы сразу же начинают двигаться обратно и через некоторое время встречаются на расстоянии 400 метров от другого берега. Какова ширина реки??
Два парома одновременно отплывают от противоположных берегов реки и пересекают ее перпендикулярно берегам. Скорости паромов постоянные, но разные. Паромы встречаются на расстоянии 720 метров от одного из берегов, после чего продолжают движение. Достигнув берегов, паромы сразу же начинают двигаться обратно и через некоторое время встречаются на расстоянии 400 метров от другого берега. Какова ширина реки??

Слайд #13
3.1. Решение уравнением
720
х-720
х+320
х-320
А
В
Для решения я вывожу формулу:
400
x- 400
720
х-720
х+320
х-320
А
В
Для решения я вывожу формулу:
400
x- 400

Слайд #14
720
S-720
S+320
S-320
А
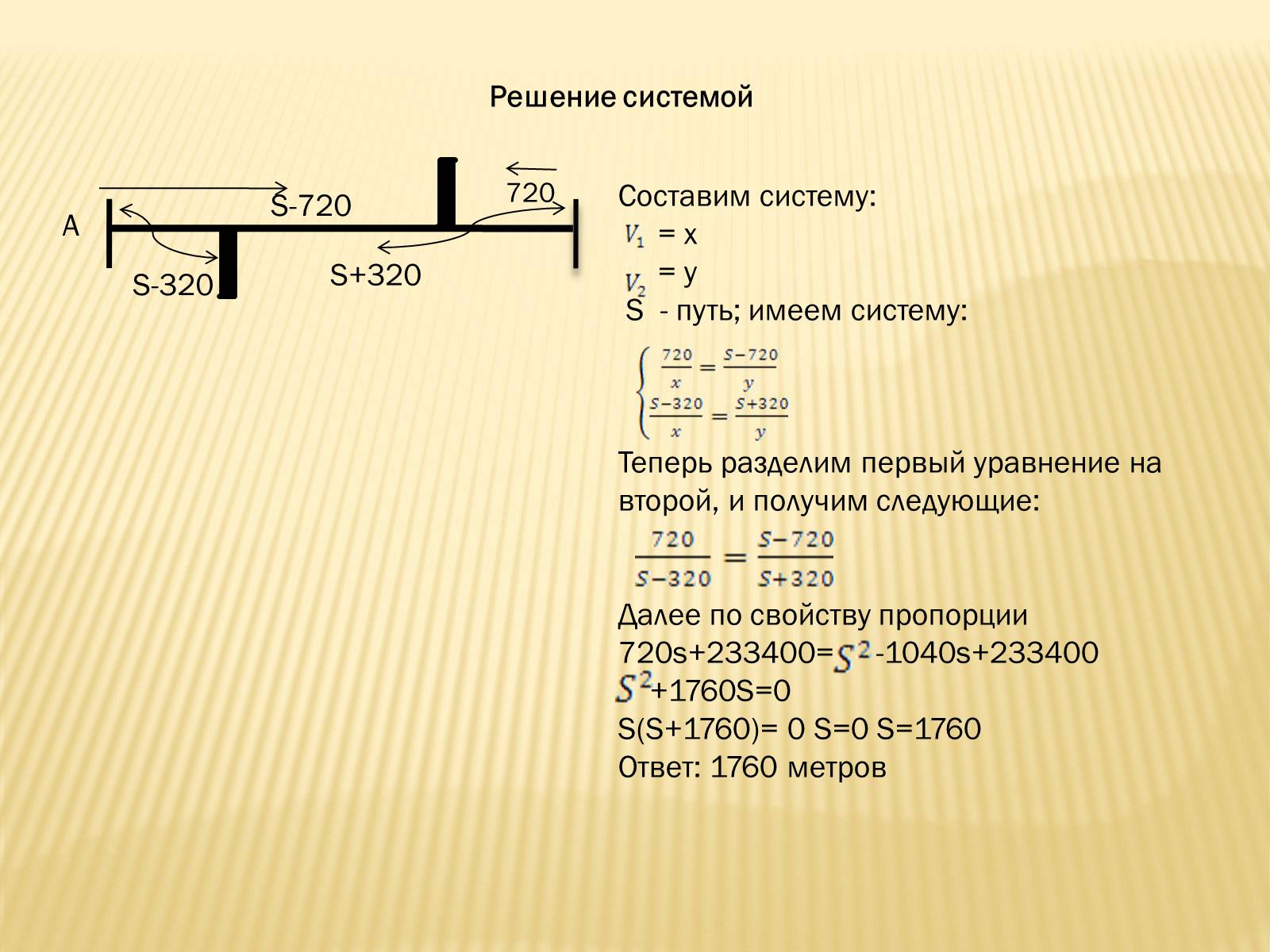
Решение системой
Составим систему:
= х
= у
S - путь; имеем систему:
Теперь разделим первый уравнение на второй, и получим следующие:
Далее по свойству пропорции
720s+233400= -1040s+233400
+1760S=0
S(S+1760)= 0 S=0 S=1760
Ответ: 1760 метров
S-720
S+320
S-320
А
Решение системой
Составим систему:
= х
= у
S - путь; имеем систему:
Теперь разделим первый уравнение на второй, и получим следующие:
Далее по свойству пропорции
720s+233400= -1040s+233400
+1760S=0
S(S+1760)= 0 S=0 S=1760
Ответ: 1760 метров
Слайд #15
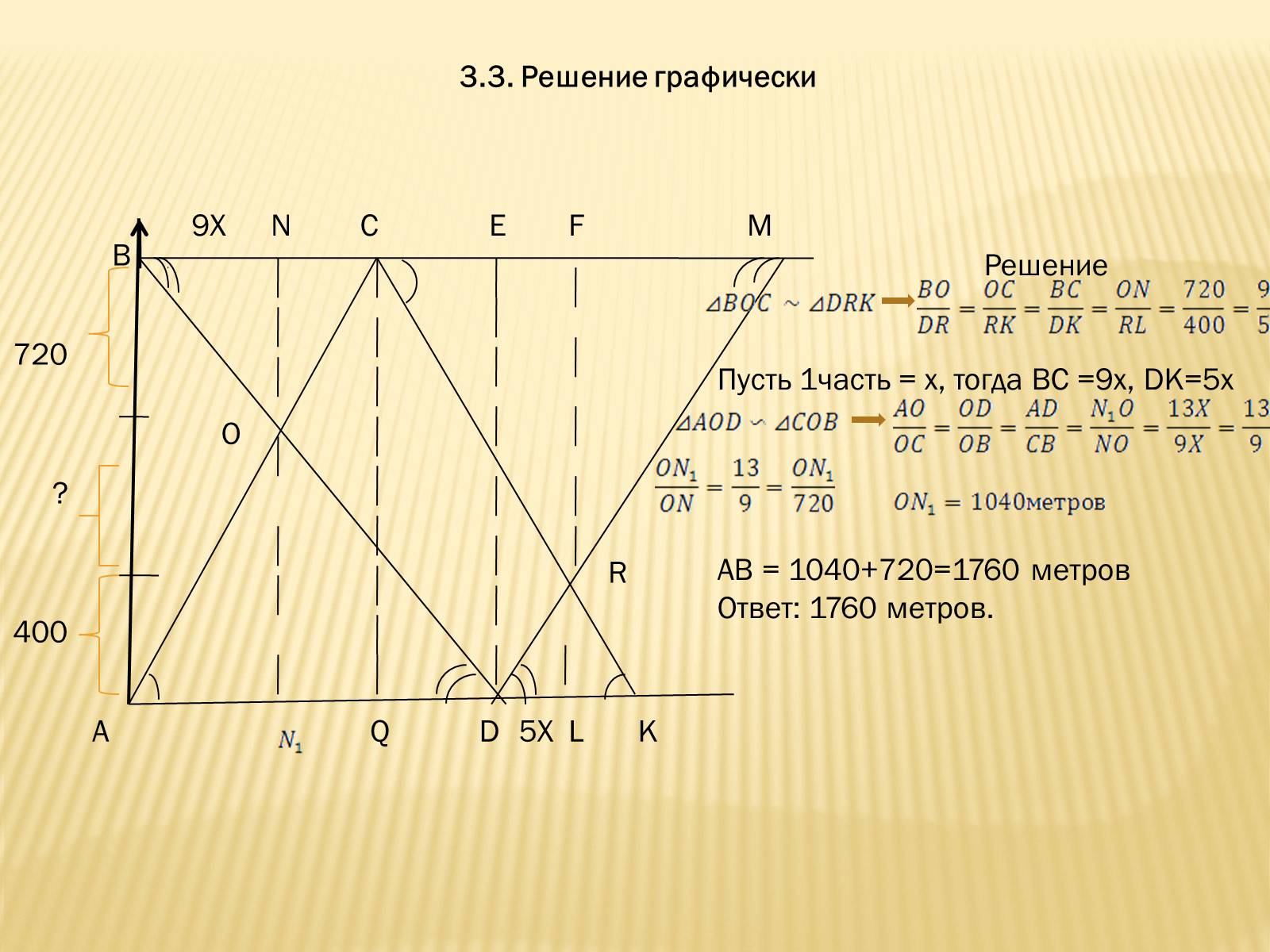
3.3. Решение графически
В
А
N
С
М
К
D
О
L
400
R
720
?
Решение
Пусть 1часть = х, тогда ВС =9х, DK=5x
АВ = 1040+720=1760 метров
Ответ: 1760 метров.
F
E
Q
5X
9X
В
А
N
С
М
К
D
О
L
400
R
720
?
Решение
Пусть 1часть = х, тогда ВС =9х, DK=5x
АВ = 1040+720=1760 метров
Ответ: 1760 метров.
F
E
Q
5X
9X
Слайд #16
Раздел 4 - Модели в виде «Графов»
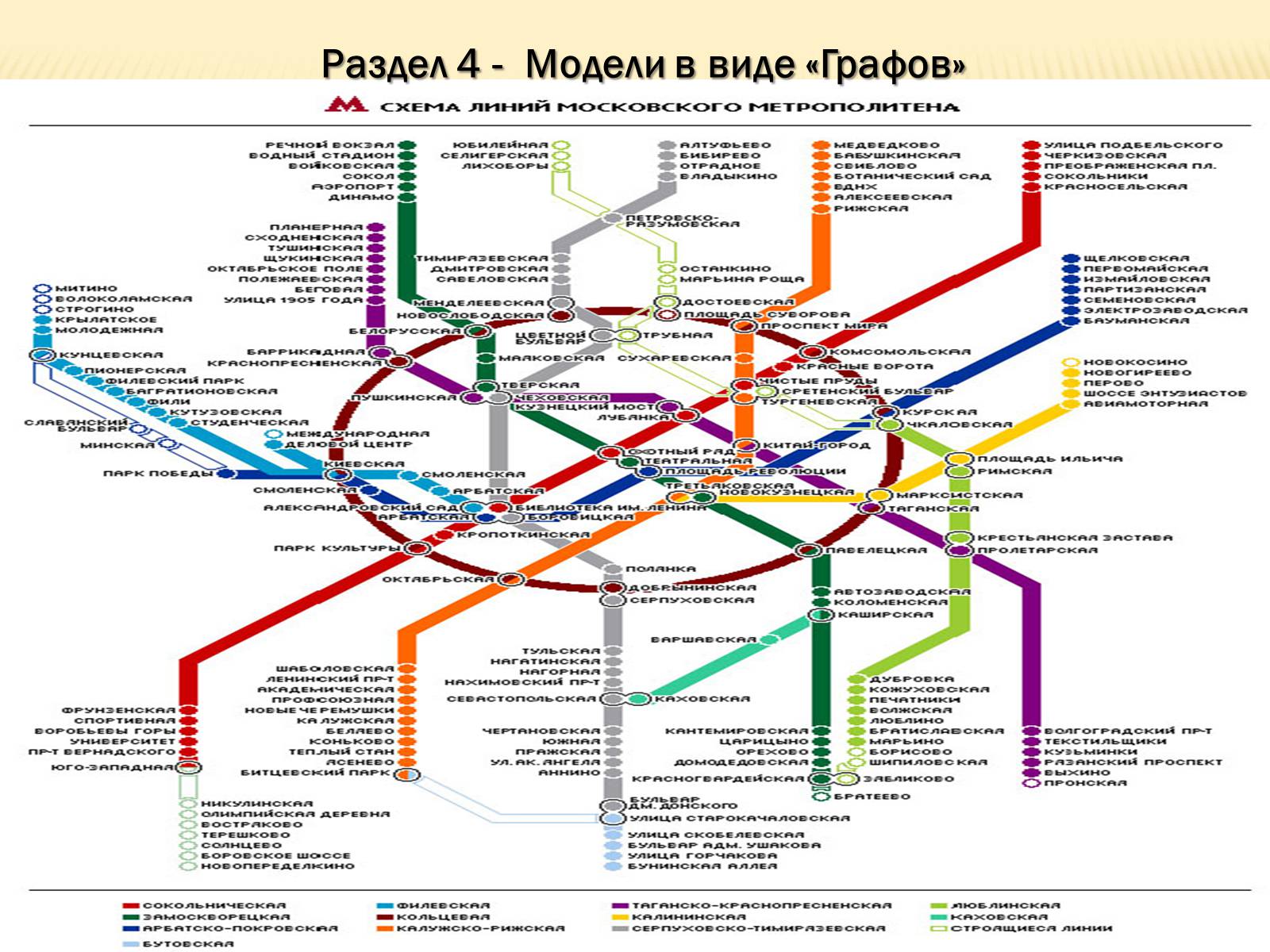
Слайд #17
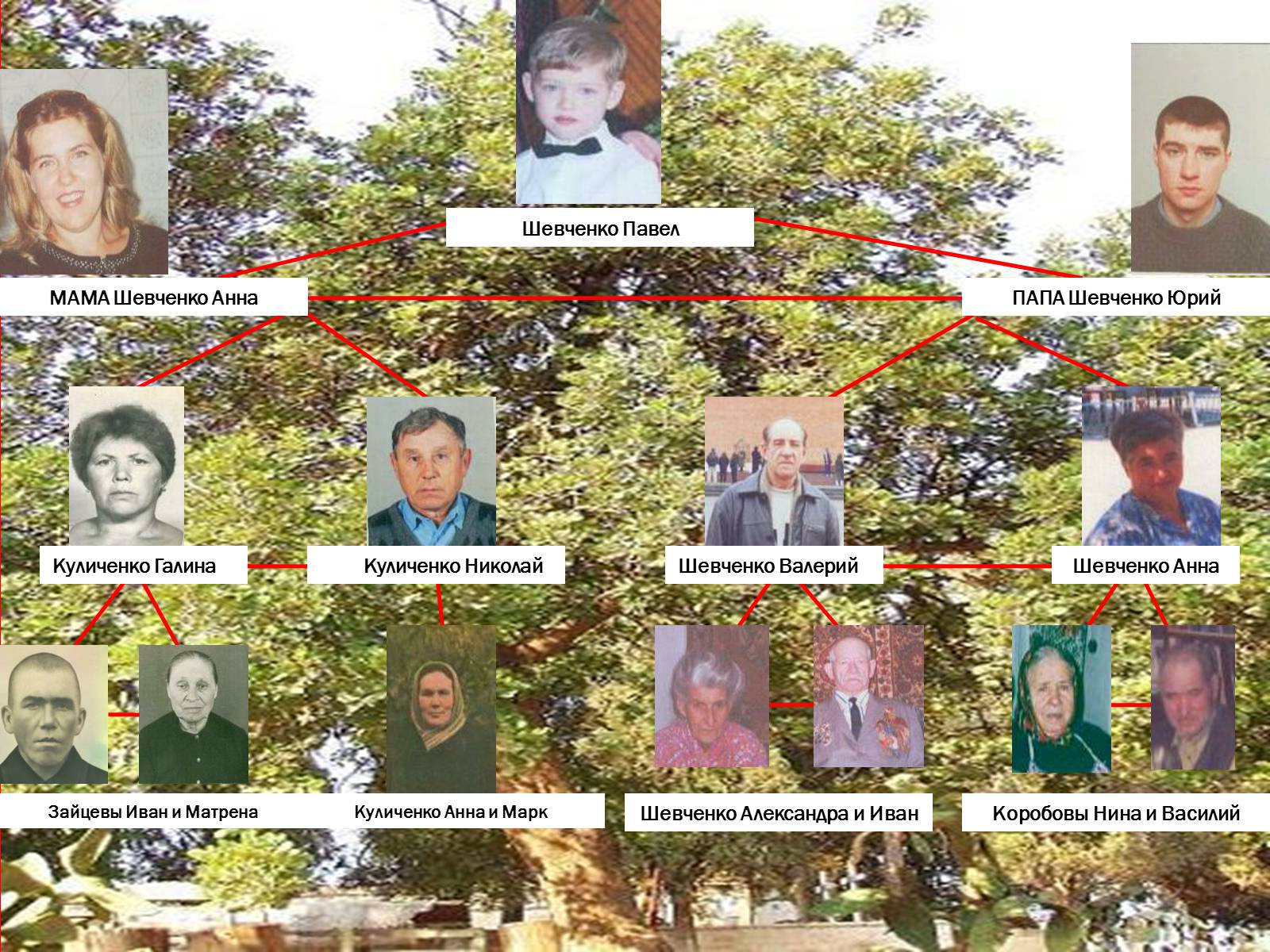
Шевченко Павел
Коробовы Нина и Василий
Шевченко Александра и Иван
Зайцевы Иван и Матрена
Куличенко Анна и Марк
МАМА Шевченко Анна
ПАПА Шевченко Юрий
Куличенко Галина
Куличенко Николай
Шевченко Анна
Шевченко Валерий
Коробовы Нина и Василий
Шевченко Александра и Иван
Зайцевы Иван и Матрена
Куличенко Анна и Марк
МАМА Шевченко Анна
ПАПА Шевченко Юрий
Куличенко Галина
Куличенко Николай
Шевченко Анна
Шевченко Валерий
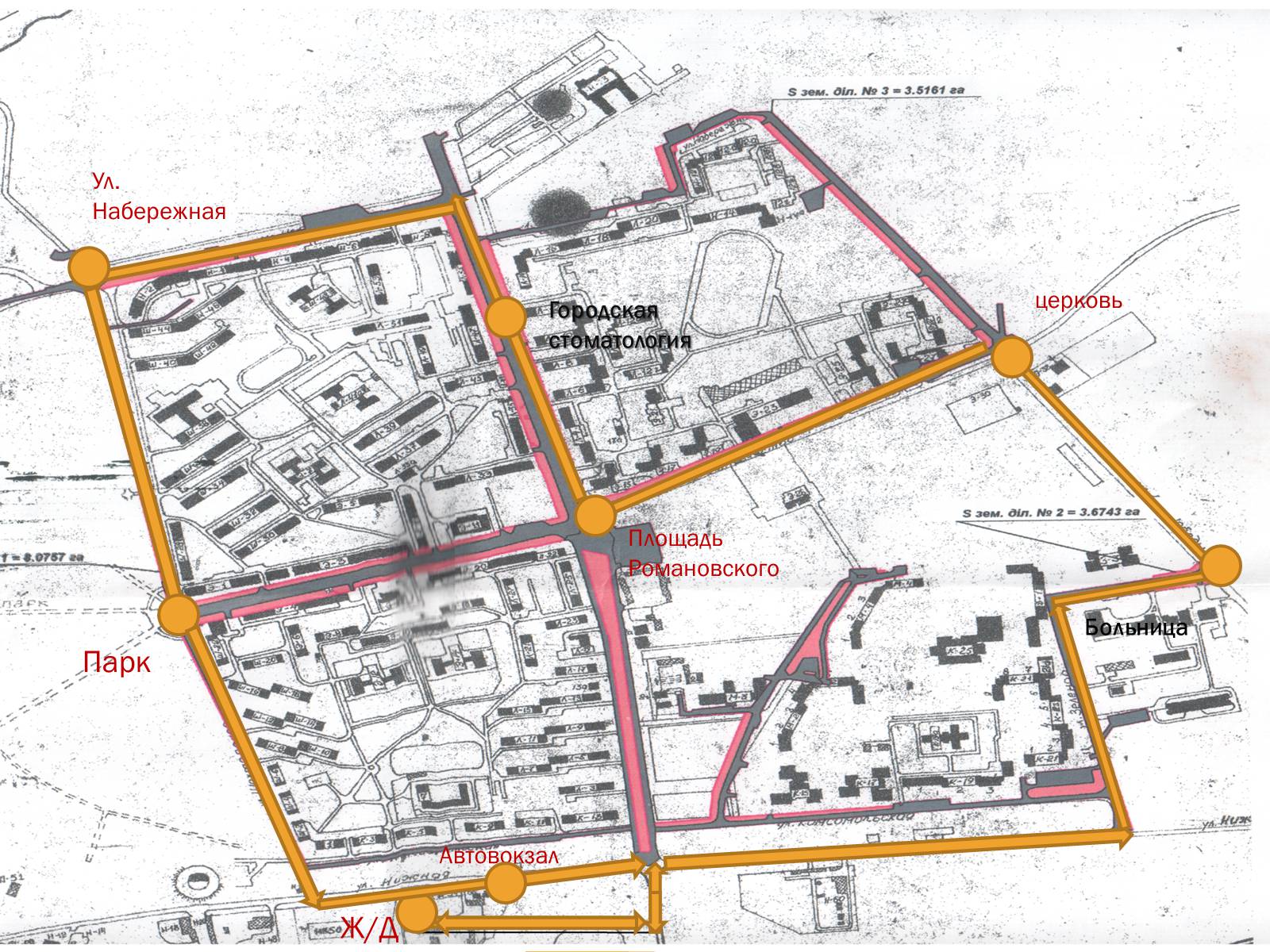
Слайд #18
Ж/Д
церковь
Площадь Романовского
Больница
Городская стоматология
Ул. Набережная
Парк
Автовокзал
церковь
Площадь Романовского
Больница
Городская стоматология
Ул. Набережная
Парк
Автовокзал
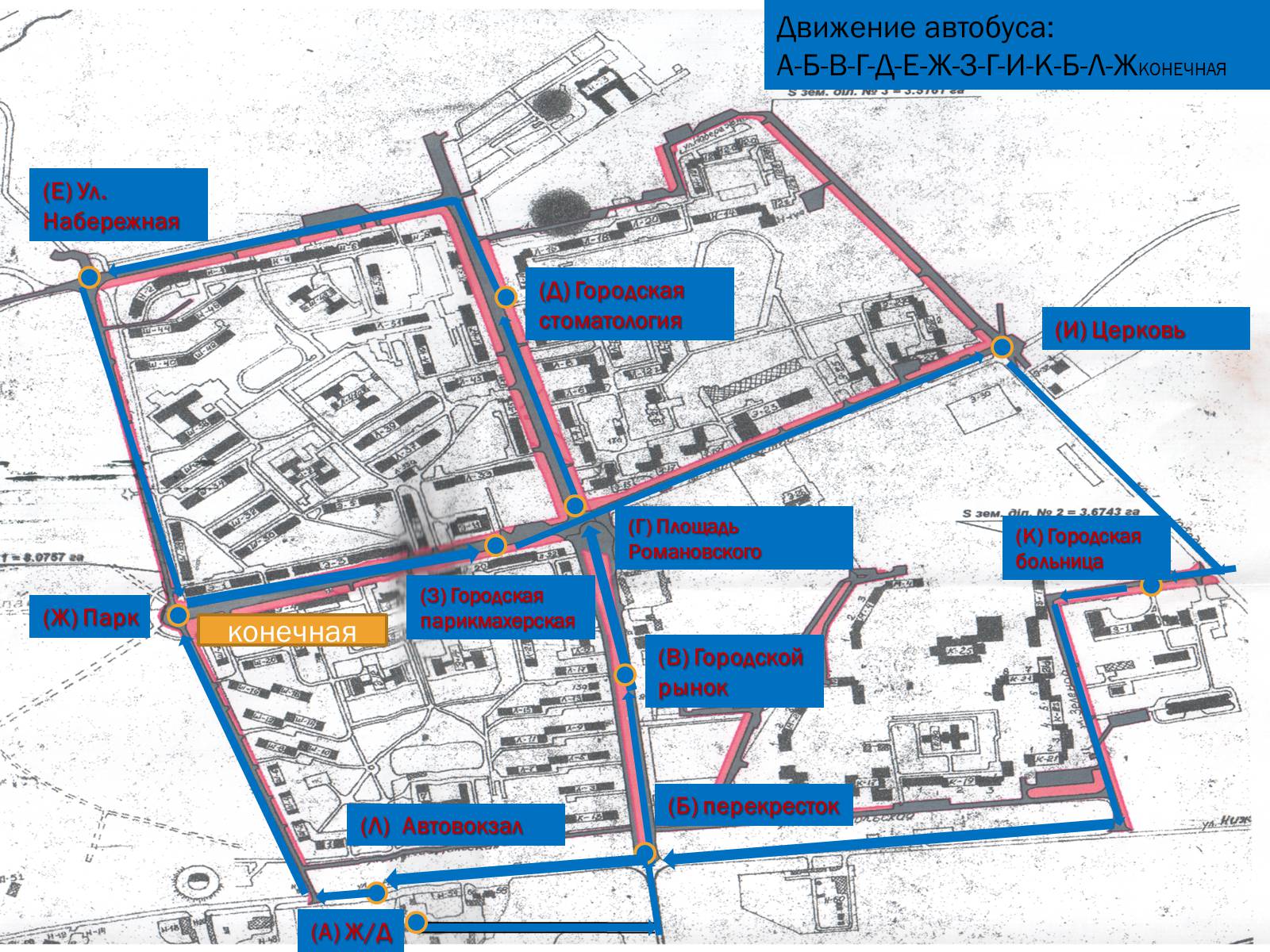
Слайд #19
конечная
(Л) Автовокзал
(К) Городская больница
(И) Церковь
(З) Городская парикмахерская
(Ж) Парк
(Е) Ул. Набережная
(Д) Городская стоматология
(Г) Площадь Романовского
(В) Городской рынок
(Б) перекресток
(А) Ж/Д
Движение автобуса:
А-Б-В-Г-Д-Е-Ж-З-Г-И-К-Б-Л-ЖКОНЕЧНАЯ
(Л) Автовокзал
(К) Городская больница
(И) Церковь
(З) Городская парикмахерская
(Ж) Парк
(Е) Ул. Набережная
(Д) Городская стоматология
(Г) Площадь Романовского
(В) Городской рынок
(Б) перекресток
(А) Ж/Д
Движение автобуса:
А-Б-В-Г-Д-Е-Ж-З-Г-И-К-Б-Л-ЖКОНЕЧНАЯ
Слайд #20
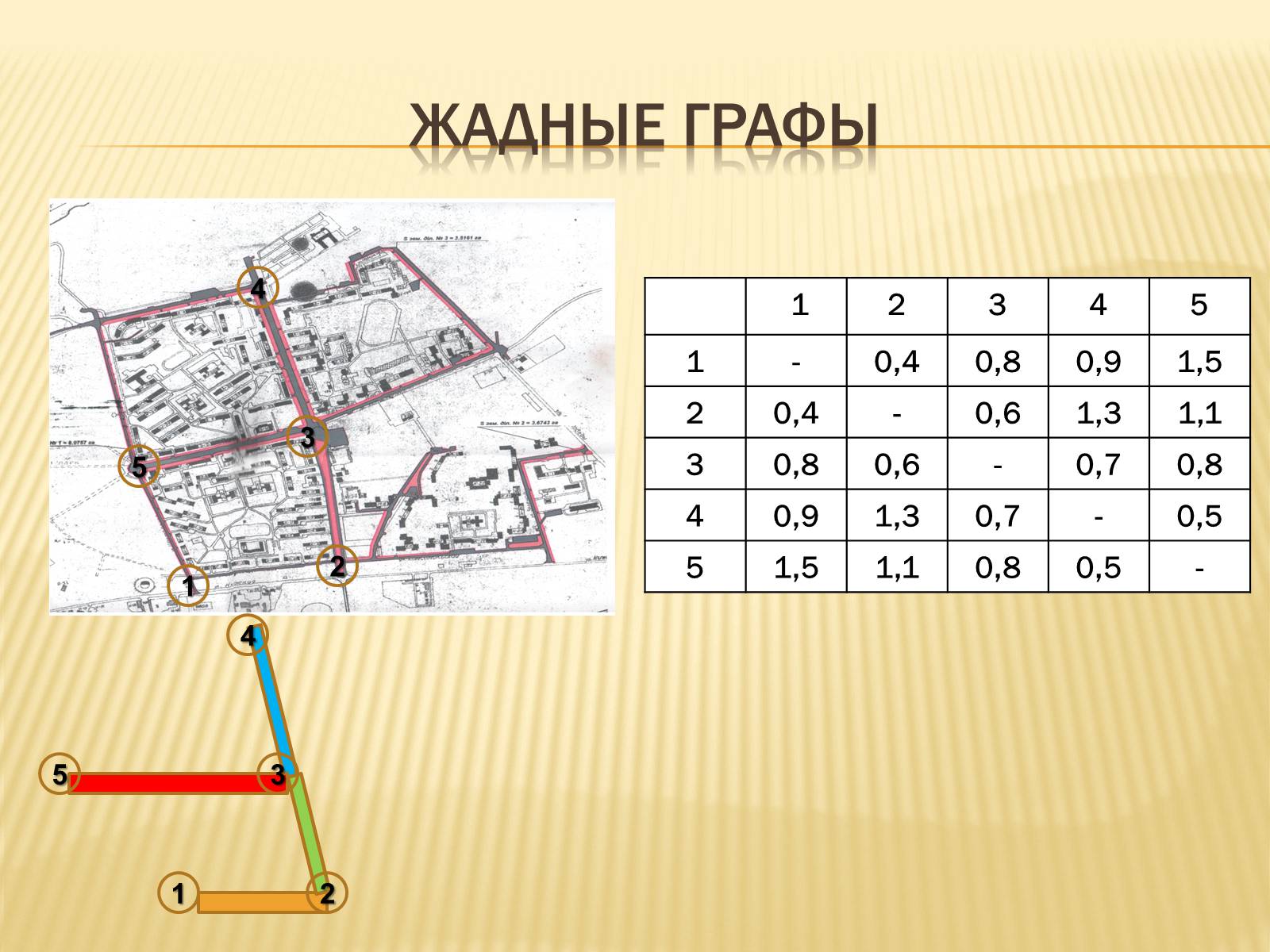
Жадные Графы
1
5
4
3
2
5
4
3
1
2
1
2
3
4
5
1
-
0,4
0,8
0,9
1,5
2
0,4
-
0,6
1,3
1,1
3
0,8
0,6
-
0,7
0,8
4
0,9
1,3
0,7
-
0,5
5
1,5
1,1
0,8
0,5
-
1
5
4
3
2
5
4
3
1
2
1
2
3
4
5
1
-
0,4
0,8
0,9
1,5
2
0,4
-
0,6
1,3
1,1
3
0,8
0,6
-
0,7
0,8
4
0,9
1,3
0,7
-
0,5
5
1,5
1,1
0,8
0,5
-
Слайд #21
Вывод
Итак в ходе работы я понял, что моделирование незаменимо в нашей жизни.
Оно помогает:
- ученикам углубленно и расширенно понимать факты.
- эффективно формировать научные понятия.
- осознано усваивать теорию, которую изучает каждая дисциплина
естественных и точных наук.
- Формированию целостной картины природы.
Итак в ходе работы я понял, что моделирование незаменимо в нашей жизни.
Оно помогает:
- ученикам углубленно и расширенно понимать факты.
- эффективно формировать научные понятия.
- осознано усваивать теорию, которую изучает каждая дисциплина
естественных и точных наук.
- Формированию целостной картины природы.

Слайд #22
Литература
1. Г.В. Апостолова В.В. Ясинский «Первая встреча с параметром»
2. Журнал «Математика в школе» 2'2003
3. Журнал « Математика в школах Украины»
4. Г.П Бевз «Алгебра 9»
5. А.Г. Берзляк В.Б. Полнский М.С. Якир «Алгебра 8»
6. «Аванта+» Энциклопедия для детей.
7. Квант 1979г. (6)
8. Интернет
1. Г.В. Апостолова В.В. Ясинский «Первая встреча с параметром»
2. Журнал «Математика в школе» 2'2003
3. Журнал « Математика в школах Украины»
4. Г.П Бевз «Алгебра 9»
5. А.Г. Берзляк В.Б. Полнский М.С. Якир «Алгебра 8»
6. «Аванта+» Энциклопедия для детей.
7. Квант 1979г. (6)
8. Интернет
