- Головна
- Готові шкільні презентації
- Презентація на тему «Показательные уравнения и неравенства»
Презентація на тему «Показательные уравнения и неравенства»
346
Слайд #1
Тема:Показательные уравнения и неравенства

Слайд #2
Это уравнение, в котором неизвестные и выражения с ними находятся в показателях каких-то степеней. И только там! Это важно.
Вот вам примеры показательных уравнений:
5х+2 = 125
3х·2х = 8х+3
32х+4·3х-5 = 0
И так далее…
Что такое показательное уравнение?
Обратите внимание! В основаниях степеней (внизу) - только числа. В показателях степеней (вверху) - самые разнообразные выражения с иксом.
Вот вам примеры показательных уравнений:
5х+2 = 125
3х·2х = 8х+3
32х+4·3х-5 = 0
И так далее…
Что такое показательное уравнение?
Обратите внимание! В основаниях степеней (внизу) - только числа. В показателях степеней (вверху) - самые разнообразные выражения с иксом.

Слайд #3
Решение простейших показательных уравнений.
Для начала решим что-нибудь совсем элементарное. Например:
3х = 32
х = 2
Что мы сделали? Мы, фактически, просто отбросили одинаковые основания (тройки).
Действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, то можно приравнять показатели степеней.
Для начала решим что-нибудь совсем элементарное. Например:
3х = 32
х = 2
Что мы сделали? Мы, фактически, просто отбросили одинаковые основания (тройки).
Действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, то можно приравнять показатели степеней.

Слайд #4
Однако, запомним: убирать основания можно только тогда, когда слева и справа числа-основания находятся в гордом одиночестве! Безо всяких соседей и коэффициентов. Скажем, в уравнениях:
2х+2х+1 = 23 или
2·2х = 24
двойки убирать нельзя!
2х+2х+1 = 23 или
2·2х = 24
двойки убирать нельзя!

Слайд #5
Вспомним действия со степенями

Слайд #6
Пример решения22х - 8х+1 = 0 8 = 23
8х+1 = (23)х+1
(аn)m = anm
8х+1 = (23)х+1 = 23(х+1)
22х - 23(х+1) = 0
22х = 23(х+1)
2х = 3(х+1)
х = -3
8х+1 = (23)х+1
(аn)m = anm
8х+1 = (23)х+1 = 23(х+1)
22х - 23(х+1) = 0
22х = 23(х+1)
2х = 3(х+1)
х = -3

Слайд #7
32х+4 -11·9х = 210
9х = (32)х = 32х
32х+4 = 32х·34
32х·34 - 11·32х = 210
32х(34 - 11) = 21032х(81 - 11) = 210
70·32х = 210
32х = 3
32х = 31
2х = 1
х = 0,5
9х = (32)х = 32х
32х+4 = 32х·34
32х·34 - 11·32х = 210
32х(34 - 11) = 21032х(81 - 11) = 210
70·32х = 210
32х = 3
32х = 31
2х = 1
х = 0,5
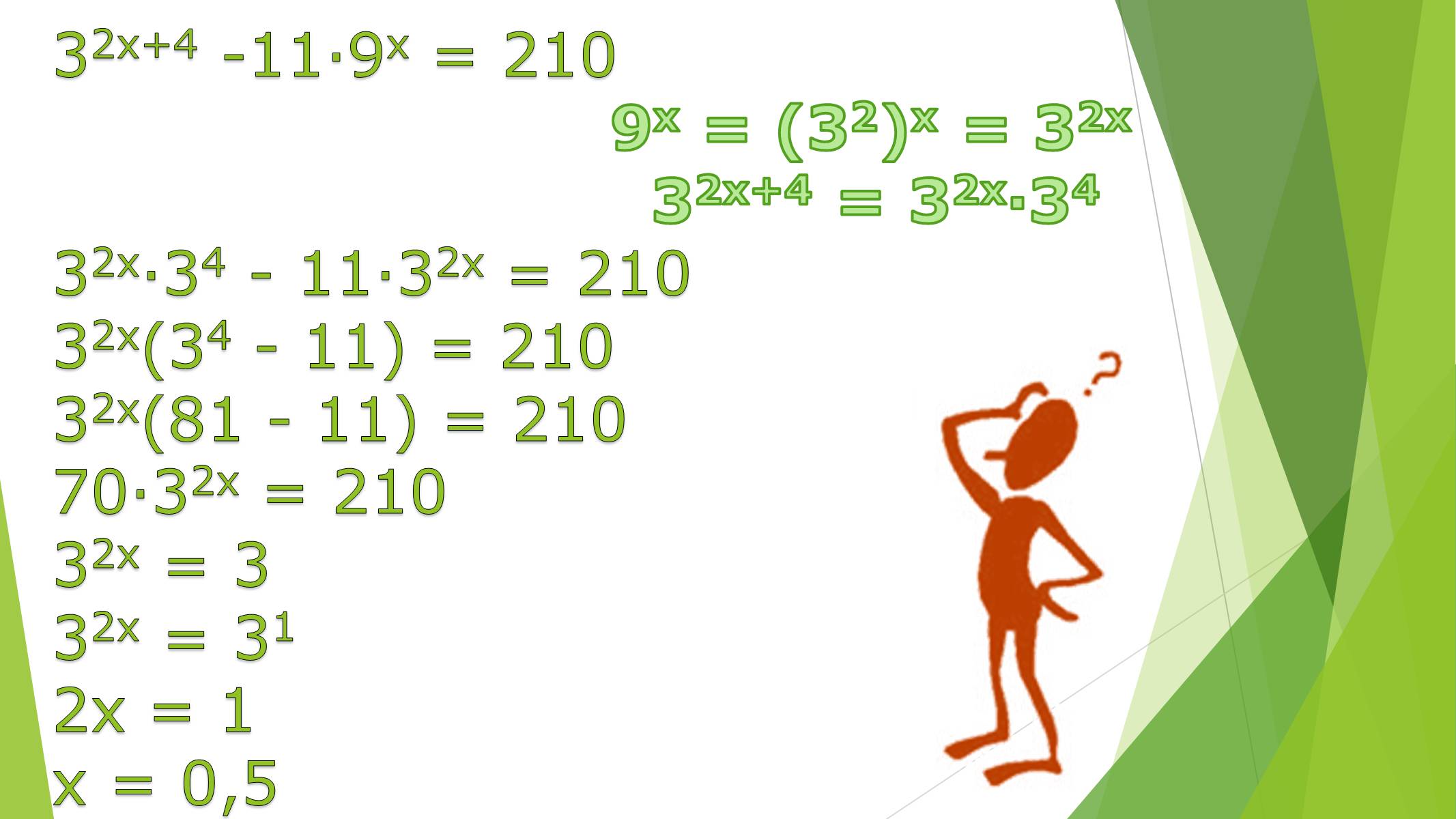
Слайд #8
Замена переменной.Биквадратные уравнения
4х - 3·2х +2 = 0 4х = (22)х = 22х
22х - 3·2х +2 = 0
2х = t Тогда 22х = 2х2 = (2х)2 = t2
.t2 - 3t+2 = 0
t1 = 2
t2 = 1.
t1 = 2 = 2х t2 = 1 = 2х
2х = 2 2х = 1
х1 = 1 1 = 20 ( 2х = 20)
х2 = 0
4х - 3·2х +2 = 0 4х = (22)х = 22х
22х - 3·2х +2 = 0
2х = t Тогда 22х = 2х2 = (2х)2 = t2
.t2 - 3t+2 = 0
t1 = 2
t2 = 1.
t1 = 2 = 2х t2 = 1 = 2х
2х = 2 2х = 1
х1 = 1 1 = 20 ( 2х = 20)
х2 = 0

Слайд #9
При решении показательных уравнений в конце иногда получается какое-то неудобное выражение. Типа:
2х = 7x = log27
2х = 7x = log27

Слайд #10
Практические советы:
1. Первым делом смотрим на основания степеней. Соображаем, нельзя ли их сделать одинаковыми. Пробуем это сделать, активно используя действия со степенями. Не забываем, что числа без иксов тоже можно превращать в степени!
2. Пробуем привести показательное уравнение к виду, когда слева и справа стоят одинаковые числа в каких угодно степенях. Используем действия со степенями и разложение на множители. То что можно посчитать в числах - считаем.
3. Если второй совет не сработал, пробуем применить замену переменной. В итоге может получиться уравнение, которое легко решается. Чаще всего - квадратное. Или дробное, которое тоже сводится к квадратному.
4. Для успешного решения показательных уравнений надо степени некоторых чисел знать "в лицо".
1. Первым делом смотрим на основания степеней. Соображаем, нельзя ли их сделать одинаковыми. Пробуем это сделать, активно используя действия со степенями. Не забываем, что числа без иксов тоже можно превращать в степени!
2. Пробуем привести показательное уравнение к виду, когда слева и справа стоят одинаковые числа в каких угодно степенях. Используем действия со степенями и разложение на множители. То что можно посчитать в числах - считаем.
3. Если второй совет не сработал, пробуем применить замену переменной. В итоге может получиться уравнение, которое легко решается. Чаще всего - квадратное. Или дробное, которое тоже сводится к квадратному.
4. Для успешного решения показательных уравнений надо степени некоторых чисел знать "в лицо".

Слайд #11
Практика

Слайд #12
Показательные неравенства

Слайд #13
Показательные неравенства

Слайд #14
Показательные неравенства

Слайд #15
Показательные неравенства

Слайд #16
Практика
