- Головна
- Готові шкільні презентації
- Презентація на тему «Спеціальна теорія відносності» (варіант 2)
Презентація на тему «Спеціальна теорія відносності» (варіант 2)
238
Слайд #1
спеціальна теорія відносності

Слайд #2
Спеціальна теорія відносності
— фізична теорія, опублікована Альбертом Ейнштейном1905 року. Вона фактично замінює класичну механіку Ньютона, яка на той час була несумісною зрівняннями Максвелла з теорії електромагнетизму.
— фізична теорія, опублікована Альбертом Ейнштейном1905 року. Вона фактично замінює класичну механіку Ньютона, яка на той час була несумісною зрівняннями Максвелла з теорії електромагнетизму.

Слайд #3
Спеціальна теорія відносності не поширює дію своїх принципів на гравітаційні сили, тому в 1916 році Ейнштейн опублікував нову — загальну теорію відносності, яка пояснювала природу гравітації.

Слайд #4
Теорія відносності та її постулати повністю змінили погляди на характеристики простору і часу. Були сформульовані основні висновки теорії відносності:
1) явища, які є одночасними в одній системі відліку, можуть виявитись неодночасними в іншій;
2) довжина тіла, час і маса залежать від швидкості тіла.
1) явища, які є одночасними в одній системі відліку, можуть виявитись неодночасними в іншій;
2) довжина тіла, час і маса залежать від швидкості тіла.

Слайд #5
м
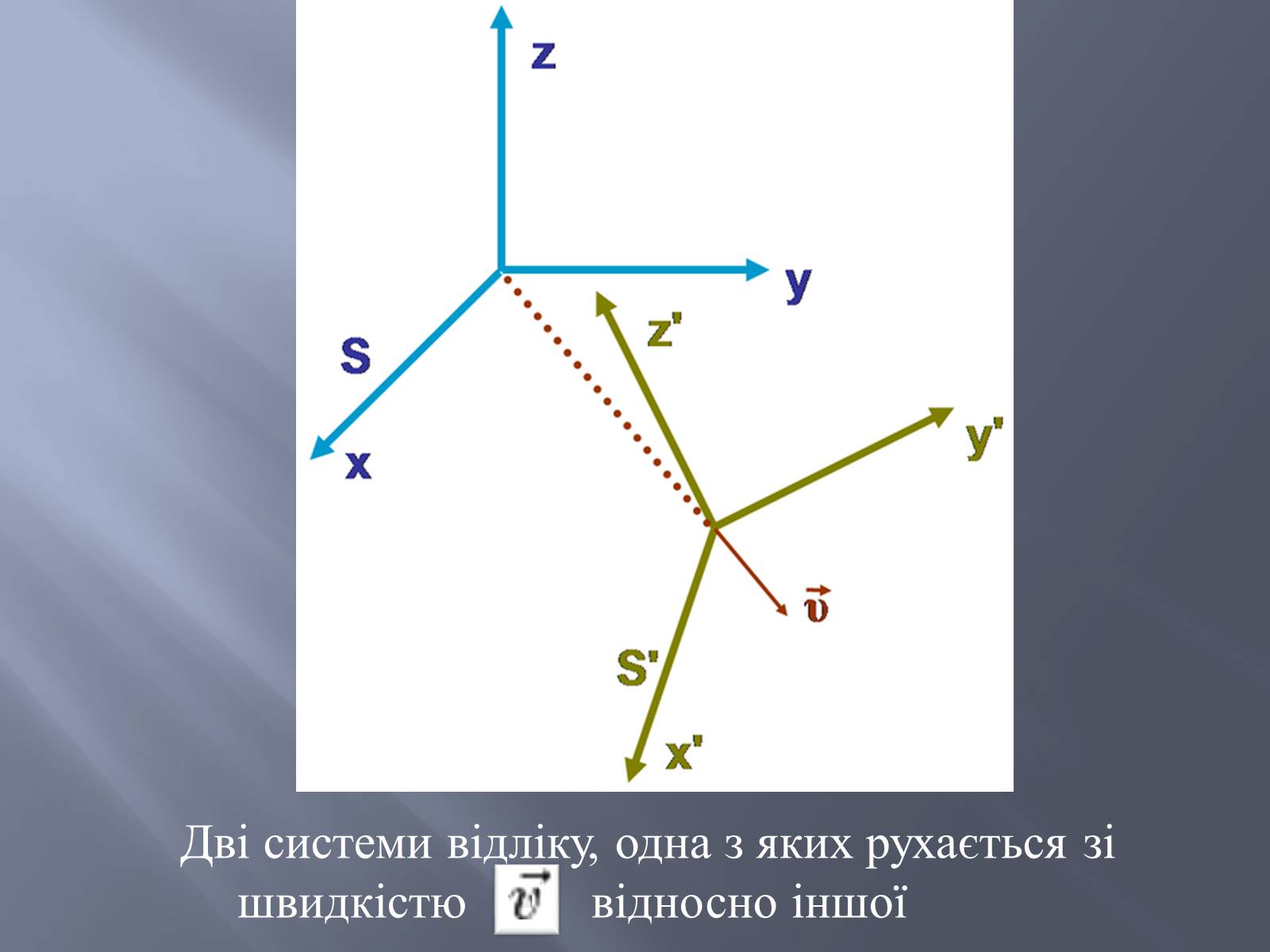
Дві системи відліку, одна з яких рухається зі швидкістю відносно іншої
Дві системи відліку, одна з яких рухається зі швидкістю відносно іншої
Слайд #6
Найбільш розповсюджена форма запису перетворень Лоренца зв'язує координати події в інерціальній системі відліку K з координатами тієї ж події в системі K′, яка рухається відносно K зі швидкістю V вздовж осі x:

Слайд #7
Інтервал. Геометричний зміст перетворень Лоренца
Інваріантність величини
, яка називається інтервалом (звичайно, його можна записати і у вигляді нескінченно малих приростів).
Інваріантність величини
, яка називається інтервалом (звичайно, його можна записати і у вигляді нескінченно малих приростів).

Слайд #8
У рамках СТВ загальний вираз для вектора сили дається похідною від вектора імпульсу:

Слайд #9
Інтервал між двома подіями
Просторо́во-часови́й інтерва́л або просто інтерва́л між двома подіями в інерційній системі відліку визначається співвідношенням:
Просторо́во-часови́й інтерва́л або просто інтерва́л між двома подіями в інерційній системі відліку визначається співвідношенням:

Слайд #10
Перетворення і додавання швидкостей
Перетворення Лоренца утворює правило додавання швидкостей. Якщо певний об'єкт має компоненти швидкості щодо системи S і - відносно S', то між ними існує наступний звязок:
Перетворення Лоренца утворює правило додавання швидкостей. Якщо певний об'єкт має компоненти швидкості щодо системи S і - відносно S', то між ними існує наступний звязок:

Слайд #11
Імпульс в релятивістській механіці
Чотирьохкомпонентний вектор, або 4-імпульс:
Імпульс частки з масою m визначається як
Чотирьохкомпонентний вектор, або 4-імпульс:
Імпульс частки з масою m визначається як

Слайд #12
Зв'язок між енергією та імпульсом тіла:
З цієї формули виходить, що об'єкти з нульовою масою, такі як фотони, також мають імпульс, який дорівнює p=E/c, де E — енергія фотона, та c — швидкість світла.
З цієї формули виходить, що об'єкти з нульовою масою, такі як фотони, також мають імпульс, який дорівнює p=E/c, де E — енергія фотона, та c — швидкість світла.

Слайд #13
Імпульс випромінений однією часткою передається до інших не миттєво, і, отже, сумарний імпульс всіх часток не зберігається. Але закон збереження виконується і в цьому випадку, якщо враховувати імпульс, що належить полю — носію взаємодії, котрому приписують густину імпульсу та густину потоку імпульсу.

Слайд #14
ВЗАЄМОЗВ'ЯЗОК МАСИ ТА ЕНЕРГІЇ
За допомогою математичних перетворень формули другого закону Ньютона А. Ейнштейн встановив, що маса тіла залежить від швидкості його руху:
За допомогою математичних перетворень формули другого закону Ньютона А. Ейнштейн встановив, що маса тіла залежить від швидкості його руху:

Слайд #15
Згідно з другим принципом СТВ, не існує систем відліку, в яких би швидкість руху тіла перевищувала швидкість поширення світла у вакуумі.

Слайд #16
Цей висновок усував існуюче протиріччя між класичною механікою і теорією відносності, оскільки за цих умов рівняння руху ставали інваріантними для всіх інерціальних систем відліку:

Слайд #17
Задача

Слайд #18
Оскільки зміна швидкості тіла впливає як на його масу, так і на енергію, природно припустити, що між цими двома величинами — масою та енергією — може існувати зв'язок. За допомогою математичних перетворень, що випливають із закону збереження енергії, А. Ейнштейн встановив спів-відношення між масою і повною енергією тіла:

Слайд #19
Формула взаємозв'язку маси та енергії відіграє особливу роль в атомній і ядерній фізиці, де перетвоення речовин унаслідок ядерних реакцій супроводжується значним вивільненням енергії. Вона має незаперечне значення і в розрахунках релятивістських ефектів елементарних частинок, зокрема під час взаємних їх перетворень.

Слайд #20
Формула взаємозв'язку маси та енергії відіграє особливу роль в атомній і ядерній фізиці, де перетвоення речовин унаслідок ядерних реакцій супроводжується значним вивільненням енергії. Вона має незаперечне значення і в розрахунках релятивістських ефектів елементарних частинок, зокрема під час взаємних їх перетворень.

Слайд #21
Фотони
і глюони
і глюони

Слайд #22
Можливі 4-імпульси тіл з нульовою і додатньою інваріантною масою. Вектори чотирьохімпульса, що побудовані від точки перетину вісей до будь-якої точки на зеленій гіперболі, мають одну і ту ж (додатню) довжину, тобто масу частинки, що несе цей чотирьохімпульс, та розрізняються енергією і 4-швидкістю частинки.
Прискорення частинки зводиться до руху кінця 4-імпульса по гіперболі. Вектори чотирьохімпульса, що побудовані від точки перетину вісей до будь-якої точки на синіх напівпрямих, мають нульову довжину и можуть відноситися лише до частинок нульової маси (наприклад, фотонів). Енергія цих частинок (з точністю до коефіцієнта c) дорівнює модулю їх 3-імпульса.
Прискорення частинки зводиться до руху кінця 4-імпульса по гіперболі. Вектори чотирьохімпульса, що побудовані від точки перетину вісей до будь-якої точки на синіх напівпрямих, мають нульову довжину и можуть відноситися лише до частинок нульової маси (наприклад, фотонів). Енергія цих частинок (з точністю до коефіцієнта c) дорівнює модулю їх 3-імпульса.

Слайд #23
В рамках підходу Ландау-Ліфшіца взаємозв'язок між швидкістю та імпульсом має вигляд:
тоді як квадрат модуля є:
тоді як квадрат модуля є:

Слайд #24
Із цих двох рівнянь можна знайти основне співвідношення, котре зв'язує масу, імпульс та енергію частинки:

Слайд #25
Очевидно, що при ( ), ми будемо мати т.з. енергію спокою:
