Презентація на тему «Використання показникової функції»

Використання показникової функції

… природа формулює свої закони мовою математики.
Галілео Галілей

у = у0ах
Показникова функція дуже часто реалізується в фізичних, біологічних та інших законах.
В житті нерідко доводиться зустрічатися з такими фактами, коли швидкість зміни деякої величини пропорційна самій величині. В цьому випадку дана величина буде змінюватися по закону, що має вигляд:

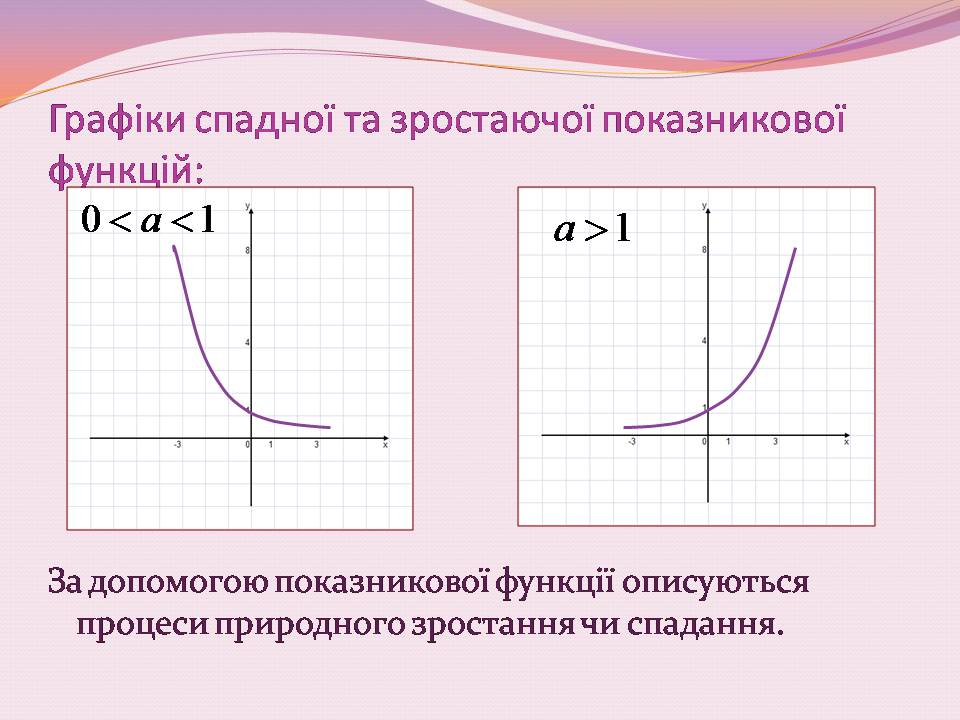
Графіки спадної та зростаючої показникової функцій:
За допомогою показникової функції описуються процеси природного зростання чи спадання.

Розмноження бактерій
де a >1 – постійна величина, що характеризує швидкість росту даної колонії і залежить від біологічного виду організмів та від умов зовнішнього середовища.
Колонія живих організмів (зокрема, бактерії) зростає в результаті розмноження. Якщо за рівні проміжки часу число живих організмів збільшується в одне й те саме число разів, то число N організмів по закінченні часу t після початку спостережень виражається формулою
N=na t

Радіоактивний розпад
М = М0(1/2)t/T
Коли радіоактивна речовина розпадається, її кількість зменшується. Через деякий час залишиться половина початкової кількості речовини. Цей проміжок часу Т називається періодом напіврозпаду речовини. Через t років маса М речовини буде дорівнювати
де М 0 – початкова маса речовини. Чим більший період напіврозпаду, тим повільніше розпадається речовина.
Явище радіоактивного розпаду використовується для визначення віку археологічних знахідок, наприклад, визначено приблизний вік Землі, біля 5,5 млрд років.

Приріст капіталу в банку
де А — шукана величина, А0, — початковий вклад, Р — річний відсоток, t — розрахунковий термін.
Приріст капіталу в банку здійснюється за законом природного зростання. Всім відома формула складних відсотків:
А = А0(1+р/100)t

Ріст населення
де N0 – кількість людей при t = 0, N – кількість людей в момент часу t,
а, e – постійні величини.
Зміна кількості людей в країні за великий проміжок часу t описується формулою:
N = N0eat

В природі і техніці часто можна спостерігати процеси, які проходять відповідно до законів вирівнювання, що описуються показниковою функцією.
Наприклад, всі, напевно, помічали, якщо зняти киплячий чайник з вогню, то спочатку він швидко охолоджується, а потім зниження температури йде набагато повільніше.
Справа в тому, що швидкість охолодження пропорційна різниці між температурою чайника і температурою навколишнього середовища. Чим меншою стає ця різниця, тим повільніше охолоджується чайник.

Т = (Т1 – Т0)е-kt + Т1
Якщо спочатку температура чайника дорівнювала Т0, а температура повітря – Т1, то через t секунд температура чайника виразиться формулою:
де k – число, що залежить форми чайника, матеріалу, з якого він зроблений та кількості води, що в ньому знаходиться.

Задача про парашутиста
де m – маса парашутиста.
Через деякий проміжок часу e-kt/m стане дуже маленьким числом і падіння стане майже рівномірним.
При падінні тіл в безповітряному просторі їх швидкість неперервно зростає. При падінні тіл в повітрі швидкість падіння також зростає, але не може перевищити визначеної величини. Розглянемо задачу про падіння парашутиста. Якщо вважати, що сила опору повітря пропорційна швидкості падіння парашутиста, тобто F = kV, то через t секунд швидкість падіння буде дорівнювати:
V = mg/k (1- e-kt/m)

Коливання маятника
Оскільки множник e-kt зменшується з плином часу, то розмах коливань стає все меншим і меншим
Якщо при коливаннях маятника не нехтувати опором повітря, то амплітуда коливань стає все меншою, коливання затухають. Відхилення точки, що здійснює затухаючі коливання, виражається формулою:
S = Ae-kt sin(ωt + φ0)

M = m(ev/v0 – 1)
Багато складних математичних задач доводиться розв'язувати в теорії міжпланетних подорожей. Одною з них є задача про визначення маси палива, необхідної для надання ракеті потрібної швидкості V. Ця маса М залежить від маси m самої ракети (без палива) і від швидкості V0, з якою продукти горіння витікають з ракетного двигуна. Якщо не враховувати опір повітря і земне тяжіння, то маса палива обчислюється за формулою:
(формула К.Е. Ціолковського)

Барометрична формула
При постійній температурі атмосферний тиск змінюється залежно від висоти над рівнем моря за законом:
Р=Р0 а h
де Р0 – атмосферний тиск над рівнем моря, Р – тиск на висоті h, а – деяка постійна (залежить від температури).

Ми  ще раз пере­коналися, що математика — це всеосяжна наука, без знання якої неможливо ні пізнати оточуючий нас світ, ні забезпечити науково-технічний прогрес. Як казав великий Ейнштейн : „Природа – це реалізація найпростіших математичних ідей”.

Як бачите, в усіх наведених дослідженнях використовувалася показникова функція.
Ось деякі з Нобелівських лауреатів, що отримали премію за дослідження в області фізики з використанням показникової функції:
П'єр Кюрі – французький фізик, лауреат Нобелівської премії з фізики в 1903 році за дослідження явища радіації.
Річардсон Оуен - англійський фізик, лауреат Нобелівської премії з фізики в 1928 році за роботи з вивчення терміонних явищ, і особливо за відкриття закону, що носить його ім'я.

Ігор Тамм — фізик-теоретик, начальник сектора конструкторського бюро № 11 (Арзамас-16), академік Академії наук СРСР, Нобелівська премія з фізики в 1958 році за дослідження теорії випромінювання Черенкова—Вавилова.
Луїс Альварес - американський фізик та винахідник, дослідник ядерної фізики та космічного випромінювання. Лауреат Нобелівської премії з фізики в 1968 році.
Ганнес Альфвен — шведський фізик і астроном, лауреат Нобелівської премії з фізики 1970 року за внесок у розвиток магнітогідродинаміки.
Роберт Вудро Вільсон, Арно Аллан Пензіасом — американські фізики, лауреати Нобелівської премії з фізики 1978 року «за відкриття мікрохвильового реліктового випромінювання».